2.2: TMS VII #2
- Page ID
- 109794
Este texto es bastante intrincado. Quien lo encuentre demasiado opaco puede omitirlo y eventualmente volver a él una vez familiarizado con el modo de pensamiento babilónico.
17 El cuarto del ancho al largo que me he unido, su séptimo
18 hasta 11 me he ido, sobre el montón
19 de largo y ancho\(5^{\prime}\) fue más allá. Tú, 4 postulan;
20 7 posit; 11 posit; y\(5^{\prime}\) posit.
21\(5^{\prime}\) a 7 subir,\(35^{\prime}\) ya ves.
22\(30^{\prime}\) y\(5^{\prime}\) postular. \(5^{\prime}\)a 11 subir,\(55^{\prime}\) ya ves.
23\(30^{\prime}\),\(20^{\prime}\), y\(5^{\prime}\), para arrancar, postular. \(5^{\prime}\)a 4
24 subir,\(20^{\prime}\) ya ves, 20 el ancho. \(30^{\prime}\)a 4 elevar:
25 2 ves, 2, longitudes. \(20^{\prime}\)de\(20^{\prime}\) arrancar.
26\(30^{\prime}\) de 2 arrancar,\(1^{\circ} 30^{\prime}\) postular, y\(5^{\prime}\) a ¿50′, el montón de largo y ancho, unir?
27 7 a 4, del cuarto, subir, 28 ya ves.
28 11, los montones, de 28 arrancan, 17 ya ves.
29 De 4, de la cuarta, 1 arranca, 3 ya ves.
30 igi 3 desprenderse,\(20^{\prime}\) ya ve. \(20^{\prime}\)a 17 elevar,
31\(5^{\circ} 40^{\prime}\) ves,\(5^{\circ} 40^{\prime}\), (para) la longitud. \(20^{\prime}\)a\(5^{\prime}\), el ir más allá, levantar,
32\(1^{\prime} 40^{\prime \prime}\) ya ves,\(1^{\prime} 40^{\prime \prime}\), el que se va a unir de la longitud. \(5^{\circ} 40^{\prime}\), (para) la longitud,
33 de 11, montones, arrancan,\(5^{\circ} 20^{\prime}\) ya ves.
34\(1^{\prime} 40^{\prime \prime}\) a\(5^{\prime}\), el ir más allá, únete,\(6^{\prime} 40^{\prime \prime}\) ya ves.
35\(6^{\prime} 40^{\prime \prime}\), el que va a ser arrancado del ancho. \(5^{\prime}\), el paso,
36 a\(5^{\circ} 40^{\prime}\), longitudes, subir,\(28^{\prime} 20^{\prime \prime}\) ya ves.
37\(1^{\prime} 40^{\prime \prime}\), la que se va a unir de la longitud, para\(28^{\prime} 20^{\prime \prime}\) unir,
38\(30^{\prime}\) ya ves,\(30^{\prime}\) la longitud. \(5^{\prime}\)a\(5^{\circ} 20^{\prime}\)
39 levantar:\(26^{\prime} 40^{\prime \prime}\) ya ves. \(6^{\prime} 40^{\prime \prime}\),
40 el que va a ser arrancado del ancho, desde el\(26^{\prime} 40^{\prime \prime}\) desgarro,
41\(20^{\prime}\) ya ves,\(20^{\prime}\) el ancho.
Este es el segundo problema difícil de una tableta. El primero, fácil (que se encuentra en la página 118 en traducción al inglés) se puede expresar en símbolos de esta manera:
\(10 \cdot\left(\frac{1}{7}\left[\ell+\frac{1}{4} w\right]\right)=\ell+w\).
Después de la reducción, esto da la ecuación
\(\ell \cdot 10=6 \cdot(\ell+w)\).
Esta es una ecuación “indeterminada”, y tiene infinidad de soluciones. Si hemos encontrado uno de ellos (\(\ell_{o}, w_{o}\)), todos los demás pueden escribirse (\(k \cdot \ell_{o}, k \cdot w_{o}\)). El texto encuentra uno tomando el primer factor a la izquierda para ser igual al primer factor a la derecha (así\(\ell=6\)), y el segundo factor a la derecha para ser igual al segundo factor a la derecha (así\(\ell+w=10\), de dónde\(w=4\)). Posteriormente la solución a la que se ha dirigido tácitamente desde el principio se obtiene a través de “subir” a\(5^{\prime}\) (el “paso”\(\frac{1}{7}\left[\ell+\frac{1}{4} w\right]\) que se ha “ido” 10 veces). En efecto\(\ell=6\), si\(w=4\), entonces el “paso” es 1; si queremos que sea\(5^{\prime}\) (que corresponde a las dimensiones normales de un “rectángulo escolar”\(\ell=30^{\prime}, w=20^{\prime}\)), entonces la solución debe multiplicarse por este valor. Todo esto —lo cual no es evidente— es útil para entender el segundo problema.
El primer problema es “homogéneo” —todos sus términos están en primer grado en\(\ell\) y\(w\). El segundo, el traducido anteriormente, no es homogéneo, y puede expresarse en símbolos de esta manera:
\(11 \cdot\left(\frac{1}{7}\left[\ell+\frac{1}{4} w\right]\right)=[\ell+w]+5^{\prime}\).
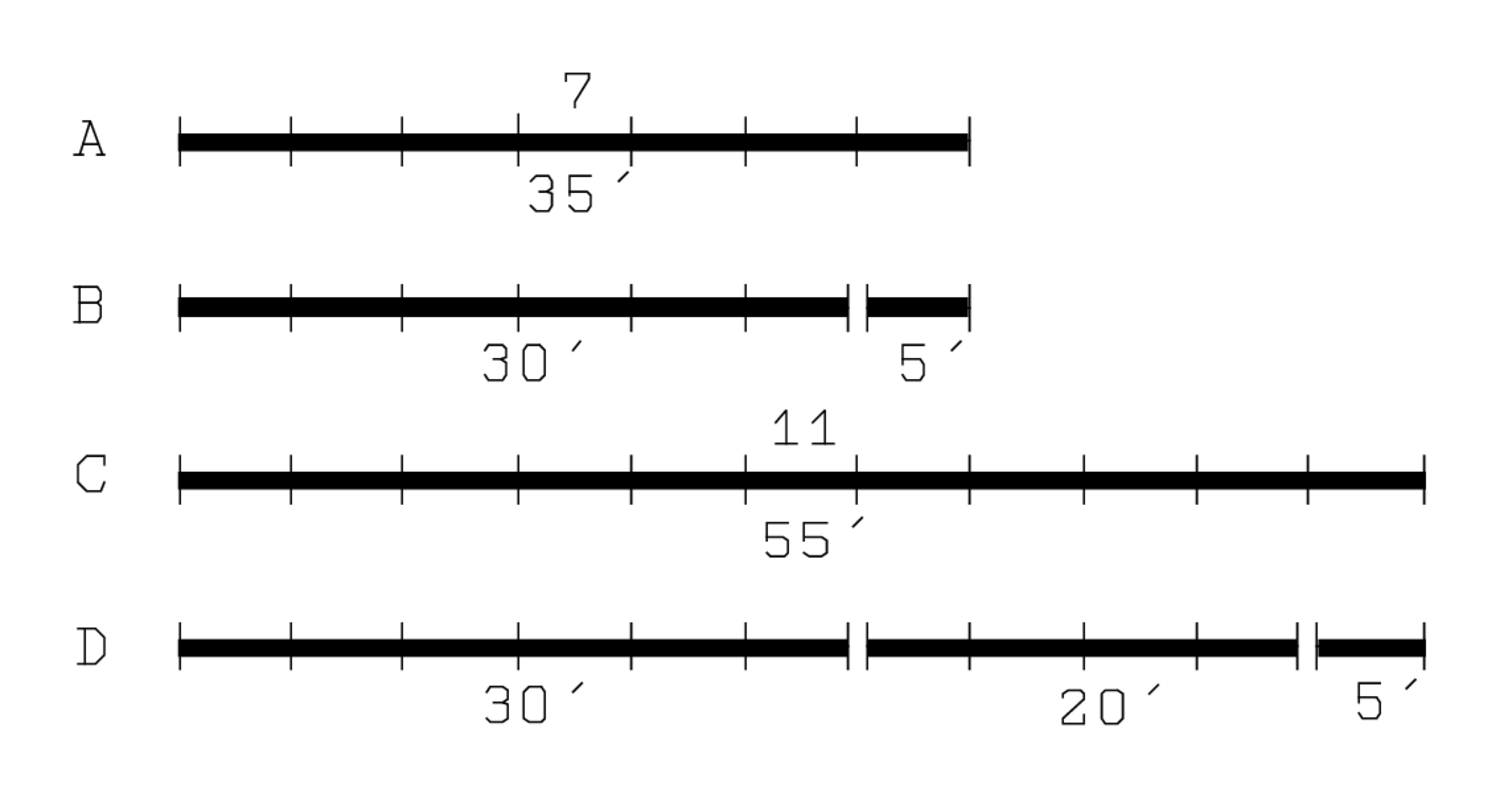
Tomamos nota que\(\frac{1}{4} w\) se “une” a la longitud; que tomamos\(\frac{1}{7}\) del desenlace; y que después “vamos” a este segmento 11 veces. Lo que resulta “va más allá” del “montón” de largo y ancho por\(5^{\prime}\). Por lo tanto, el “montón” no forma parte de lo que resulta de la repetición del paso, si fuera podría haber sido “arrancado”.
La solución comienza con una explicación pedagógica al estilo de TMS XVI #1, el cuasi-problema anterior. Al leer bien vemos que el\(5^{\prime}\) que se “eleva” a 7 en la línea 21 debe ser el “paso”\(\frac{1}{7}\left[\ell+\frac{1}{4} w\right]\) —el levantar es una verificación de que realmente es el séptimo— y no el “ir más allá” al que se refiere en la línea 20. Una vez más se supone que el alumno entienda que el texto se basa en el rectángulo
(\(30^{\prime}\),\(20^{\prime}\)). Teniendo esta configuración en mente podremos seguir la explicación de las líneas 21 a 23 en la Figura 2.7: cuando el “paso”\(5^{\prime}\) se “eleva” a 7, obtenemos\(35^{\prime}\) (A), que se puede descomponer como\(\ell\) y\(\frac{1}{4} w\) (B). Cuando se “eleva” a 11 nos encontramos con\(55^{\prime}\) (C), que puede descomponerse como\(\ell\),\(w\), y\(5^{\prime}\) (D).
A continuación sigue la prescripción para resolver la ecuación; ¿todavía está formulada de tal manera que se supone que se conoce la solución? “Elevar” a 4 (líneas 23 a 25) da el equivalente de la ecuación simbólica
\(11 \cdot\left(\frac{1}{7}\left[4 \ell+4 \cdot \frac{1}{4} w\right]\right)=4 \cdot\left([\ell+w]+5^{\prime}\right)\).
Al no tener acceso a nuestros símbolos, el texto habla de\(\frac{1}{4} w\) como\(5^{\prime}\), encuentra que\(4 \cdot \frac{1}{4} w\) es igual a\(20^{\prime}\), e identifica eso con el ancho (línea 24); luego\(4 \ell\) aparece como 2, dice que representa longitudes (línea 25).
Ahora bien, por medio de una artimaña elegante pero no fácil de seguir, la ecuación se hace homogénea. El texto se descompone\(4 \ell+w\) como
\((4-1) \ell-5^{\prime}+(w-w)+\left(\ell+w+5^{\prime}\right)\)
y “eleva” toda la ecuación a 7. Podemos seguir el cálculo en la traducción simbólica moderna:
\ (\ begin {aligned}
11\ cdot\ left ([4-1]\ ell-5^ {\ prime} +0+\ left [\ ell+w+5^ {\ prime}\ right]\ right) & =( 7\ cdot 4)\ cdot\ left ([\ ell+w] +5^ {\ prime}\ right)\\
\ Leftrightarrow\ quad 11\ cdot\ izquierda ([4-1]\ ell-5^ {\ prime}\ derecha) & =( 28-11)\ cdot\ izquierda ([\ ell+w] +5^ {\ prime}\ derecha)\\
&=17\ cdot\ izquierda ([\ ell+w] +5^ {\ prime}\ derecha)\
\ Trightarrow izquierda\ quad 11\ cdot\ izquierda (\ ell-\ frac {1} {3}\ cdot 5^ {\ prime}\ derecha) &=\ frac {1} {3}\ cdot 17\ cdot\ izquierda (\ ell+w+5^ {\ prime}\ derecha)\\
\ Leftrightarrow\ quad\ izquierda (\ ell-1^ {\ prime} 40^ {\ prime\ prime}\ derecha)\ cdot 11 &=5^ {\ circ} 40^ {\ prime}\ cdot\ izquierda (\ ell+w+5^ {\ prime}\ derecha)
\ end {alineado}\).
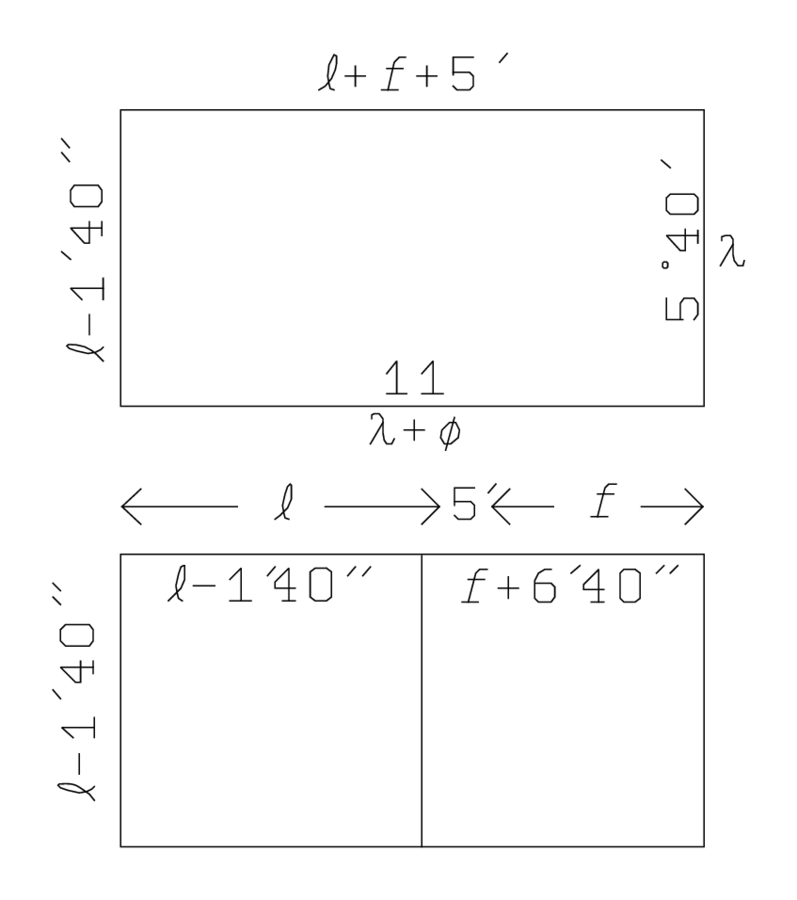
Sin embargo, los babilonios no operaron con tales ecuaciones; es probable que hayan inscrito los números a lo largo de las líneas de un diagrama (Figura 2.8); esa es la razón por la que el “coeficiente”\((4-1)\) no necesita aparecer antes de la línea 29.
Al igual que en el primer problema del texto, se encuentra una solución a la ecuación homogénea mediante la identificación de los factores “a la izquierda” con aquellos “a la derecha” (que es la razón de que los factores se han invertido en el lado izquierdo de la última ecuación):\(\ell-1^{\prime} 40^{\prime \prime}\) (ahora llamado “la longitud” y por lo tanto designado\(\lambda\) en la Figura 2.8 corresponde así a\(5^{\circ} 40^{\prime}\), mientras que\(\ell+w+5^{\prime}\) (referido como “el montón” de la nueva longitud\(\lambda\) y un nuevo ancho\(\phi\), es decir,\(\lambda+\phi\)) es igual a 11; por lo tanto,\(\phi\) debe ser\(11-5^{\circ} 40^{\prime}=5^{\circ} 20^{\prime}\). A continuación el texto determina el “a unir” (wāṣbum) de la longitud, es decir, aquello que se debe unir a la longitud\(\lambda\) para producir la longitud original\(\ell\): es igual\(1^{\prime} 40^{\prime \prime}\), ya que\(\lambda=t-1^{\prime} 40^{\prime \prime}\). Además encuentra “el que va a ser arrancado” (nāsum) del ancho, es decir, aquello que debe ser “arrancado” para producir\(w\).\(\phi\) Ya que\(\ell+w+5^{\prime}=11\),\(w\) debe ser igual\(11-\ell-5^{\prime}=11-\left(\lambda+1^{\prime} 40^{\prime \prime}\right)-5^{\prime}=(11-\lambda)-\left(1^{\prime} 40^{\prime \prime}+5^{\prime}\right)=\phi-6^{\prime} 40^{\prime \prime}\); el “a ser arrancado” es así\(6^{\prime} 40^{\prime \prime}\).
Pero “unirse”\(\lambda\) y “arrancar”\(\phi\) solo da una solución posible, no la que se pretende. Para tener los valores para\(\ell\) y\(w\) que van dirigidos, el paso\(5^{\prime}\) es “elevado” (como en el primer problema) a\(5^{\circ} 40^{\prime}\) y\(5^{\circ} 20\). Esto da, respectivamente,\(28^{\prime} 20^{\prime \prime}\) y\(26^{\prime} 40^{\prime \prime}\); al “unir” al primero su “por unir” y al “arrancar” de este último su “a ser arrancado” finalmente conseguimos\(\ell=30^{\prime}, w=20^{\prime}\).
Debemos tomar nota del dominio con el que el autor evita hacer uso en el procedimiento de su conocimiento de la solución (excepto al final, donde necesita conocer el “paso” para escoger la solución a la que se dirige entre todas las posibles soluciones). Los valores numéricos que se conocen sin ser dados sirven en las explicaciones pdegógicas; posteriormente, su función es proporcionar nombres —sin símbolos como\(\ell\) y\(\lambda\), el babilónico necesita usar identificaciones como “la longitud\(30^{\prime}\)" y” la longitud 5^ {\ prime} 40^ {\ prime\ prime}” (ambas son longitudes, por lo que el nombre “longitud” sin ningún calificador no será suficiente).
Los valores numéricos sirven como identificadores en muchos textos; sin embargo, los malentendidos resultantes de una mezcla de números dados y simplemente conocidos son extremadamente raros.