3.1: BM 13901 #1
- Page ID
- 109672
Obv. I
1 La superficie y mi confrontación me han colmado:\(45^{\prime}\) es. 1, la proyección,
2 postula. El resto de 1 te rompes,\(30^{\prime}\) y\(30^{\prime}\) te aferras.
3\(15^{\prime}\) a\(45^{\prime}\) que te unes: por 1, 1 es igual. \(30^{\prime}\)que has hecho sostener
4 desde el interior de 1 arrancas:\(30^{\prime}\) el enfrentamiento.
Este es el problema que se citó en la página 9 en la “transliteración” de los asiriólogos y en la página 13 en una traducción tradicional. Una traducción al simbolismo matemático moderno se encuentra en la página 12.
A pesar de que lo conocemos bien desde este punto de vista, volveremos a examinar el texto y la terminología en detalle para poder tratarlo desde la perspectiva de su autor.
La línea 1 plantea el problema: trata de una superficie, aquí un cuadrado, y de su correspondiente enfrentamiento, es decir, la configuración cuadrada parametrizada a su lado, ver página 22. Es la aparición del “enfrentamiento” lo que nos dice que la “superficie” es la de un cuadrado.
Se apilan “superficie” y “confrontación”. Esta adición es la que se debe utilizar cuando se trata de magnitudes disímiles, aquí un área (dos dimensiones) y un lado (una dimensión). El texto dice la suma de las dos magnitudes, es decir, de sus números de medición:\(45^{\prime}\). Si\(c\) representa el lado del cuadrado y
(\(c\)) por su área, el problema puede expresarse así en símbolos de esta manera:
\(\square(c)+c=45^{\prime}\left(=\frac{3}{4}\right)\).
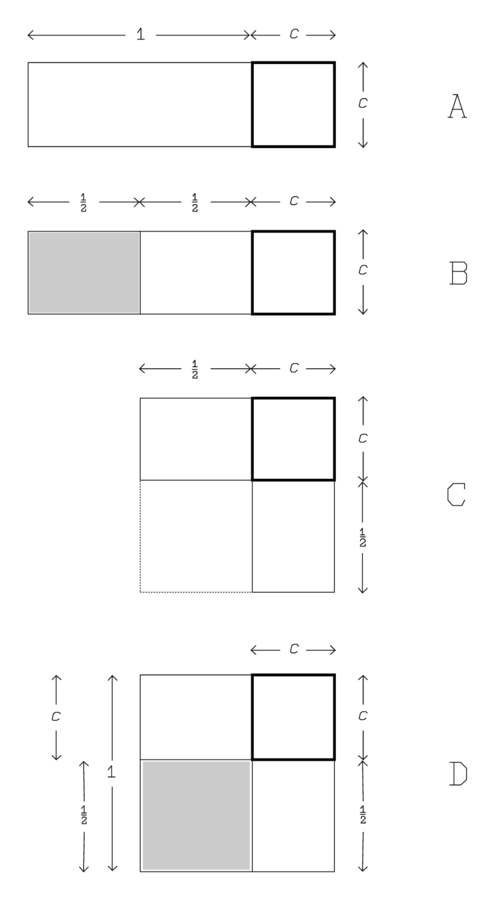
La Figura 3.1 muestra los pasos del procedimiento que conduce a la solución tal y como se explican en el texto:
A: 1, la proyección, usted postula. Eso significa que un rectángulo
(\(c\),1) se dibuja junto al cuadrado\(\square\) (\(c\)). De esta manera, la suma de una longitud y un área, absurda en sí misma, se hace geométricamente significativa, es decir, como un área rectangular\((c, c+1)=\frac{3}{4}=45^{\prime}\). Esta interpretación geométrica explica la apariencia de la “proyección”, ya que el rectángulo (\(c\),1) “sobresale” de la plaza como una proyección que sobresale de un edificio. Recordamos (ver página 15) que la palabra fue traducida originalmente como “unidad” o “coeficiente” simplemente porque los traductores no entendían cómo un número 1 podía “proyectar”.
B: El resto de 1 se rompe. La “proyección” con rectángulo adyacente
(\(c\),1) se “rompe” en dos mitades “naturales”.
C:\(30^{\prime}\) y\(30^{\prime}\) te aferras. La mitad exterior de la proyección (sombreada en gris) se mueve alrededor de tal manera que sus dos partes (cada una de longitud\(30^{\prime}\)) “sujetan” el cuadrado con borde punteado debajo a la izquierda. Este procedimiento de cortar y pegar nos ha permitido así transformar el rectángulo
(\(c\),\(c+1\)) en un “gnomón”, un cuadrado del que falta un cuadrado más pequeño en una esquina.
D:\(15^{\prime}\) a\(45^{\prime}\) ti te unes: 1. \(15^{\prime}\)es el área de la plaza sostenida por las dos mitades (\(30^{\prime}\)y\(30^{\prime}\)), y\(45^{\prime}\) la del gnomón. Como recordamos de la página 18, “unir” una magnitud a otra es una ampliación de esta última y sólo es posible si ambas son concretas y del mismo tipo, por ejemplo áreas. Así nos “unimos” a la plaza faltante, completando de esta manera el gnomon para conseguir una nueva plaza. El área de la plaza terminada será\(45^{\prime}+15^{\prime}=1\).
por 1, 1 es igual. En general, la frase “por\(Q\),\(s\) es igual” significa (ver página 23) que el área\(Q\) trazada como un cuadrado tiene\(s\) como uno de sus lados iguales (en lenguaje aritmético,\(s=\sqrt{Q}\)). En el presente caso, el texto nos dice así que el lado de la plaza terminada es 1, como se indica en D inmediatamente a la izquierda del cuadrado.
\(30^{\prime}\)que has hecho sostener desde el interior de 1 arrancas. Para encontrar el lado\(c\) del cuadrado original debemos ahora quitar esa pieza de longitud\(\frac{1}{2}=30^{\prime}\) que se le agregó a continuación. Para “arrancar”\(a\)\(H\), como hemos visto en la página 18, es la operación inversa de una “unión”, una eliminación concreta que presupone que en realidad\(a\) es parte de\(H\). Como se observó anteriormente (página 15), la frase “desde adentro” se omitió de las primeras traducciones, siendo carente de sentido siempre y cuando se suponía que todo tratara de números abstractos. Si en cambio el número 1 representa un segmento, la frase sí tiene sentido.
\(30^{\prime}\)el enfrentamiento. Al quitar de 1 el segmento\(\frac{1}{2}=30^{\prime}\) que se agregó, obtenemos el lado inicial\(c\), el “enfrentamiento”, que de ahí es igual a\(1-30^{\prime}=30^{\prime}=\frac{1}{2}\) (extrema izquierda en D).
Eso soluciona el problema. En esta interpretación geométrica, no sólo se explican los números sino también las palabras y explicaciones utilizadas en el texto.
La nueva traducción exige cierta observación. Tomamos nota de que no se da ningún argumento explícito de que el procedimiento de cortar y pegar lleve a un resultado correcto. Por otro lado es intuitivamente claro que debe ser así. Podemos hablar de un enfoque “ingenuo”, teniendo en cuenta que nuestra forma normal de operar en ecuaciones, por ejemplo en el ejemplo resolviendo el mismo problema en la página 12, no es menos ingenua. Así como la vieja calculadora babilónica procedemos de paso a paso sin dar ninguna prueba explícita de que las operaciones que realizamos están justificadas, “viendo” meramente que son apropiadas.
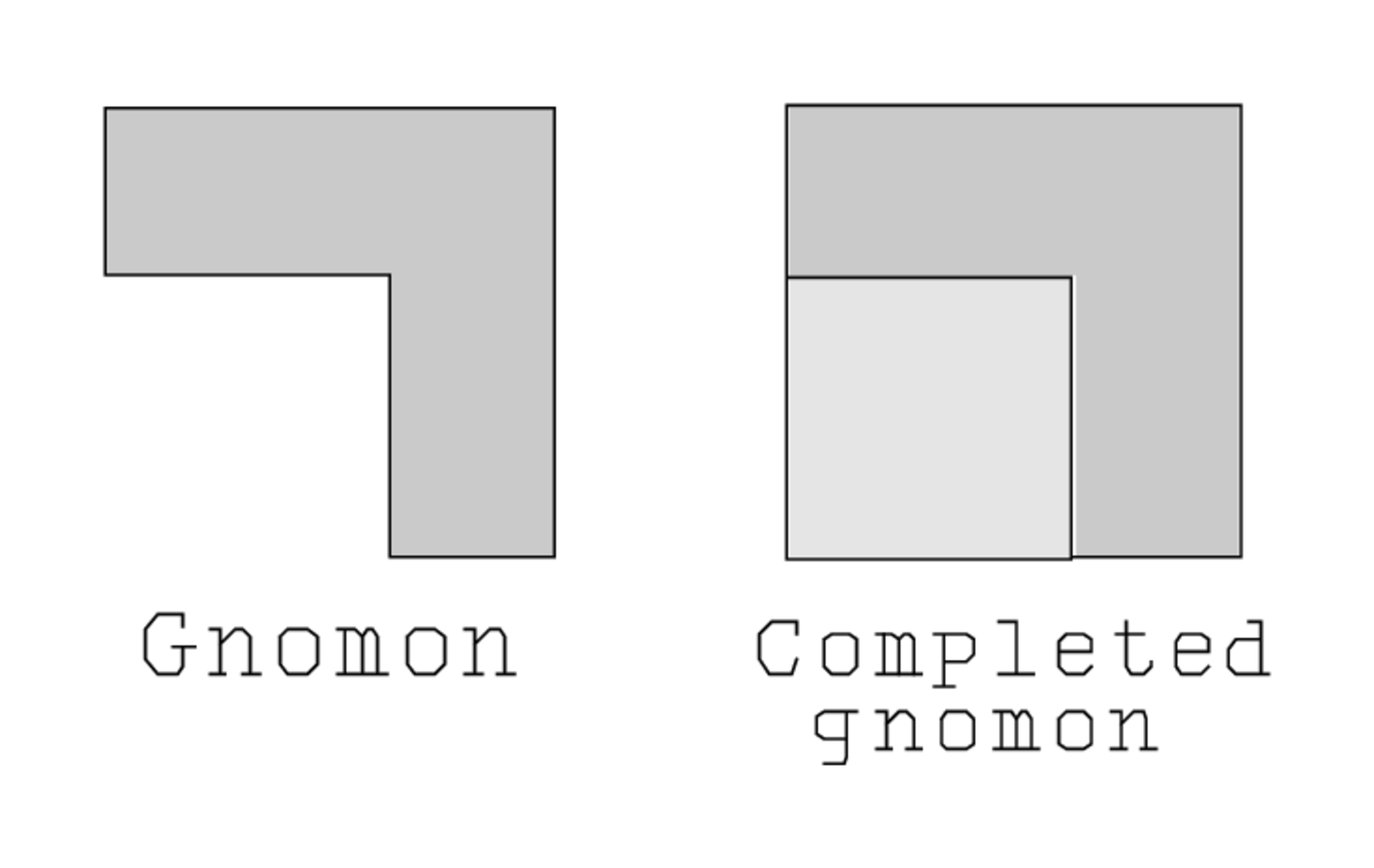
La estratagema esencial del método babilónico antiguo es la finalización del gnomón como se muestra en la Figura 3.2. Esta estratagema se denomina “finalización cuadrática”; se emplea el mismo término sobre el paso correspondiente en nuestra solución por medio de símbolos
\ (\ begin {alineado}
x^ {2} +1\ cdot x=\ frac {3} {4} &\ Leftrightarrow x^ {2} +1\ cdot x+\ izquierda (\ frac {1} {2}\ derecha) ^ {2} =\ frac {3} {4} +\ izquierda (\ frac {1} {2}\ derecha) ^ {2}\\
&\ Izquierda fila x^ {2} +1\ cdot x+\ izquierda (\ frac {1} {2}\ derecha) ^ {2} =\ frac {3} {4} +\ frac {1} {4} =1\\
&\ Izquierda fila\ izquierda (x+\ frac {1} {2}\ derecha) ^ {2} =1
\ end {alineado}\).
No obstante, el nombre parece aplicarse aún mejor al procedimiento geométrico.
Es obvio que una solución negativa no tendría sentido en esta interpretación concreta. El antiguo álgebra babilónica se basaba en cantidades tangibles incluso en los casos en que sus problemas no eran realmente prácticos. Ninguna longitud (ni superficie, volumen o peso) podría ser negativa. La única idea que se encuentra en los textos babilónicos antiguos que se aproximan a la negatividad es que una magnitud puede ser sustractiva, es decir, predeterminada para ser arrancada. Hemos encontrado tales magnitudes en el texto TMS XVI #1 (líneas 3 y 4—ver página 27) así como TMS VII #2 (línea 35, el “a ser arrancado del ancho” —ver página 34). En la línea 25 de este último texto también observamos que los babilonios no consideraron el resultado de una resta\(20^{\prime}\) de\(20^{\prime}\) como un número sino, literalmente, como algo de lo que no vale la pena hablar.
Ciertas exposiciones generales de la historia de las matemáticas afirman que los babilonios sí conocían números negativos. Esta es una leyenda basada en la lectura descuidada. Como se mencionó, algunos textos señalan por razones de estilo no que una magnitud\(A\) supere a otra por la cantidad\(d\) sino que\(B\) queda por debajo de\(A\) por\(d\); encontraremos un ejemplo en BM 13901 #10, ver nota 4, página 46. En sus comentarios matemáticos Neugebauer expresó estos como respectivamente\(A-B=d\) y\(B-A=-d\) (\(A=B+d\)y\(B=A-d\) habría estado más cerca de los textos antiguos, pero incluso Neugebauer tenía sus razones de estilo). De esta manera, los matemáticos que sólo leen las traducciones en fórmulas y no las explicaciones del significado de estas (y desde luego no los textos traducidos) encontraron sus números negativos “babilónicos”.
Como escribió el orientalista francés Léon Rodet en 1881 al criticar las interpretaciones modernizadoras de un antiguo papiro matemático egipcio:
Para estudiar la historia de una ciencia, así como cuando uno quiere obtener algo, 'es mejor tener negocios con Dios que con sus santos'. 1