3.2: BM 13901 #2
- Page ID
- 109649
Obv. I
5 Mi enfrentamiento dentro de la superficie me he arrancado:\(14^{\prime} 30\) es. 1, la proyección,
6 postula. El resto de 1 te rompes,\(30^{\prime}\) y\(30^{\prime}\) te aferras,
7\(15^{\prime}\) a\(14^{\prime} 30\) que te unes: por\(14^{\prime} 30^{\circ} 15^{\prime}\),\(29^{\circ} 30^{\prime}\) es igual.
8\(30^{\prime}\) que has hecho\(29^{\circ} 30^{\prime}\) aferrarte a ti: 30 el enfrentamiento.
Este problema, en una tableta que contiene en total 24 problemas de creciente sofisticación tratando con uno o más cuadrados, sigue inmediatamente después del que acabamos de examinar.
Desde el punto de vista babilónico antiguo así como el nuestro, es su contraparte “natural”. Donde el precedente “se une”, éste “arranca”. La parte básica del procedimiento es idéntica: la transformación de un rectángulo en un gnomón, seguida de un complemento cuadrático.
Inicialmente se plantea el problema (línea 5): Mi enfrentamiento dentro de la superficie me he arrancado:\(14^{\prime} 30\) es. Una vez más el problema se refiere así a una zona y un costado cuadrados, pero esta vez\(c\) se “arranca” el “enfrentamiento”.
“arrancar” es una resta concreta por remoción, la inversa de la operación de “unión”, utilizada sólo cuando aquello que se “arranca” forma parte de esa magnitud de la que se “arranca”. 2 El “enfrentamiento”\(c\) se ve así como parte de (el interior de) la zona. La Figura 3.3, A muestra cómo esto es posible: la “confrontación” c está provista de una anchura (una “proyección”) 1 y con ello se cambia a un rectángulo (\(c\),1), ubicado dentro del cuadrado. Este rectángulo (sombreado en gris oscuro) debe ser así “arrancado”; lo que queda después de haber eliminado
(\(c\),1), ubicado dentro del cuadrado. Este rectángulo (sombreado en gris oscuro) debe ser así “arrancado”; lo que queda después de haber eliminado (\(c\),1) de
(\(c\),1) de (\(c\)) debería ser\(14^{\prime} 30\). En los símbolos modernos, el problema corresponde a
(\(c\)) debería ser\(14^{\prime} 30\). En los símbolos modernos, el problema corresponde a
\(\square(c)-c=14^{\prime} 30\).
Una vez más, nos queda un rectángulo para el que conocemos el área (\(14^{\prime} 30\)) y la diferencia entre la longitud (\(c\)) y la anchura\((c-1)\) —y una vez más, esta diferencia equivale a 1, es decir, la “proyección.
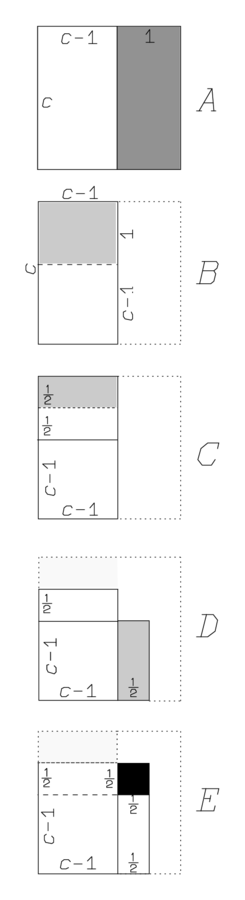
 \((c, c-1)\)está compuesto por un cuadrado (blanco) y un rectángulo “sobrante” (sombreado) cuyo ancho es la proyección 1.
\((c, c-1)\)está compuesto por un cuadrado (blanco) y un rectángulo “sobrante” (sombreado) cuyo ancho es la proyección 1. \((c, c-1)\), es decir, igualar a\(14^{\prime} 30\).
\((c, c-1)\), es decir, igualar a\(14^{\prime} 30\).A continuación, se encuentran el área de la plaza terminada y su lado:\(15^{\prime}\) a\(14^{\prime} 30\) ti te unes: por\(14^{\prime} 30^{\circ} 15^{\prime}\),\(29^{\circ} 30^{\prime}\) es igual.
Volviendo a poner el “resto” que se movió alrededor, nos encontramos con el costado de la plaza inicial, que resulta ser\(29^{\circ} 30^{\prime}+30^{\prime}=30\): a la\(30^{\prime}\) que te has hecho\(29^{\circ} 30^{\prime}\) aferrarte:\(30\) el enfrentamiento.
Notamos que esta vez el “enfrentamiento” de la plaza es\(30\), no\(30^{\prime}\). La razón es simple y convincente: a menos\(c\) que sea mayor que 1, el área será más pequeña que el lateral, y tendríamos que “arrancar” más de lo que está disponible, lo que evidentemente no se puede hacer. Como ya se explicó, los babilonios estaban familiarizados con “magnitudes sustractivas”, es decir, magnitudes que están predeterminadas para ser “arrancadas”; pero nada en su pensamiento matemático correspondía a nuestros números negativos.
También notamos que el par (\(14^{\prime} 30^{\circ} 15^{\prime}\),\(29^{\circ} 30^{\prime}\)) no aparece en la tabla de cuadrados y raíces cuadradas (ver página 23); el problema se construye así hacia atrás a partir de una solución conocida.


