5.1: IVA 8512
- Page ID
- 109626
Obv.
1 Un triángulo. 30 el ancho. En el interior de dos parcelas,
2 la superficie superior sobre la superficie inferior,\(7`\) fue más allá.
3 El descendiente inferior sobre el descendiente superior, 20 fue más allá.
4 Los descendientes y el bar ¿qué?
5 Y las superficies de las dos parcelas ¿qué?
6 Usted, 30 la posición de ancho,\(7`\) que la superficie superior sobre la superficie inferior fue más allá de postular,
7 y 20 que el descendiente inferior sobre el descendiente superior fue más allá del postulado.
8 igi 20 que el descendiente inferior sobre el descendiente superior fue más allá
9 desprender:\(3^{\prime}\) a\(7`\) lo que la superficie superior sobre la superficie inferior fue más allá
¡10 subir, 21 que te sostenga la cabeza!
11 21 a 30 la unión de ancho: 51
12 junto con 51 hacen sujeción:\(43`21\)
13 21 que tu cabeza sostiene unida con 21
14 hacer bodega:\(7`21\) para\(43`21\) unirse:\(50`42\).
Descanso de 15\(50`42\) a dos:\(25`21\).
16 ¿El igual de\(25`21\) qué? 39.
17 Del 39, 21 el desgarro hecha-sostén, 18.
18 18 que te queda es el listón.
19 Bueno, si 18 es el listón,
20 los descendientes y las superficies de las dos parcelas ¿qué?
21 Tú, 21 que junto consigo mismo has hecho aferrarse, de 51
22 arrancan: 30 te vas. 30 que te quedan
23 a dos break, 15 a 30 que te queda subir,
¡24\(7`30\) que tu cabeza sostenga!
Edge
1 18 la barra junto con 18 hacen que sostenga:
2\(5`24\) de\(7`30\) la que sostiene tu cabeza
3 arranca:\(2`6\) te vas.
Rev.
1 Qué\(2`6\) puedo postular
2 lo\(7`\) que la superficie superior sobre la superficie inferior fue más allá me da?
3\(3^{\circ} 20^{\prime}\) posit. \(3^{\circ} 20^{\prime}\)para\(2`6\) levantar,\(7`\) te da.
4 30 el ancho sobre 18 la barra ¿qué va más allá? 12 va más allá.
5 12 a los\(3^{\circ} 20^{\prime}\) que se ha postulado raise, 40.
6 40 el descendiente superior.
7 Bueno, si 40 es el descendiente superior,
8 la superficie superior es ¿qué? Tú, 30 el ancho,
9 18 el montón de barras: 48 a dos descanso: 24.
10 24 a 40 la subida descendiente superior,\(16`\).
11\(16`\) la superficie superior. Bueno, si\(16`\) la superficie superior,
12 el descendiente inferior y la superficie inferior ¿qué?
13 Tú, 40 el descendiente superior a 20 que el descendiente inferior sobre el descendiente superior va más allá
14 unirse,\(1`\) el descendiente inferior.
15 18 la barra a dos se rompen: 9
16 a\(1`\) la subida descendiente inferior,\(9`\).
17\(9`\) la superficie inferior.
Muchos problemas matemáticos babilónicos antiguos tratan de la partición de campos. La sustancia matemática puede variar, a veces la forma del campo es irrelevante y solo se da el área junto con las condiciones específicas para su división; a veces, como aquí, lo que se pide es una división de una forma geométrica particular.
Ya antes de 2200 a. C., los topógrafos mesopotámicos supieron dividir un trapecio en dos partes iguales por medio de una transversal paralela; volveremos en poco tiempo a cómo lo hicieron. Una división similar de un triángulo no se puede hacer exactamente sin el uso de números irracionales, lo que significa que no podría ser realizada por las antiguas calculadoras babilónicas (excepto con aproximación, que no estaba entre los objetivos normales de enseñanza).
El problema actual se refiere a una variante de la división triangular que se puede realizar exactamente. Como vemos en las líneas Obv. 1—3 y como se muestra en la Figura 5.1, un campo triangular se divide en dos parcelas (una “superficie superior” y una “superficie inferior”) por una “barra”, es decir, una transversal paralela. Por simplicidad podemos suponer que el triángulo es rectangular. Es casi seguro que el autor del texto hizo tanto, y que los “descendientes” son así parte del lado; pero si interpretamos a los “descendientes” como alturas, los cálculos también son válidos para un triángulo oblicuo.
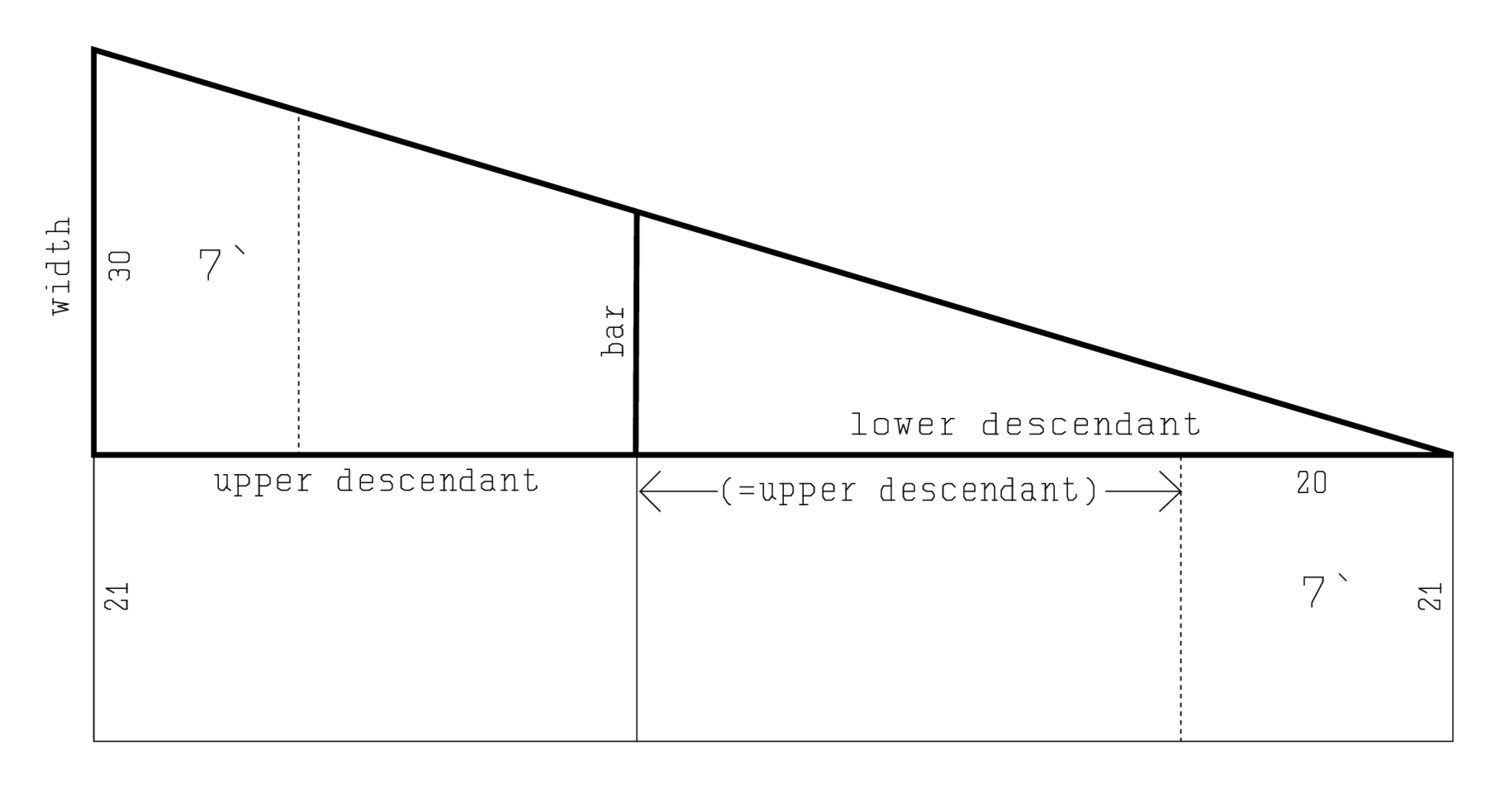
Las dos parcelas son así desiguales en área. No obstante, conocemos la diferencia entre sus áreas, así como la diferencia entre los “descendientes” apurtenant. La solución hace uso de una artimaña insospechada y elegante y, por lo tanto, puede ser difícil de seguir.
Líneas Obv. 8-10 “elevan” el igi de la diferencia entre los dos “descendientes” a la diferencia entre las dos “superficies”. Esto significa que el texto encuentra el ancho de un rectángulo cuya longitud corresponde a la diferencia entre las alturas parciales y cuya área es igual a la diferencia entre las áreas parciales. Este ancho (que es 21) primero se memoriza y luego se “une” al ancho del triángulo.
El resultado es un triángulo con un rectángulo adjunto, todo en todo el trapecio que se muestra en la Figura 5.1. Al prolongar la barra, produciendo una transversal paralela del trapecio, descubrimos que divide el trapecio en dos partes iguales, y ese es el problema que los topógrafos habían sabido resolver desde hace medio milenio o más.
Líneas Obv. 11-16 muestra cómo lo habían hecho: el cuadrado en la transversal bisectriz se determina como el promedio entre los cuadrados de los lados paralelos. las operaciones que se utilizan (“hacer retención” y “romper”) muestran que el proceso es realmente pensado en términos de cuadrados geométricos y promedio. La figura (5.2) muestra por qué el procedimiento conduce al resultado correcto. Por definición, el promedio es equidistante de los dos extremos. Por lo tanto, el gnomón entre 21 y 39 debe ser igual al que está entre 39 y 51\(\left(39^{2}-21^{2}=51^{2}-39^{2}\right)\); por lo tanto, la mitad de estos gnomones —las dos partes del trapecio sombreado— también deben ser iguales. En primera instancia esto solo se refiere a un trapecio recortado a lo largo de la diagonal de un cuadrado, pero podemos imaginar el cuadrado dibujado largo (en un rectángulo) y tal vez retorcido en un paralelogramo; ninguna de estas operaciones cambia la relación entre ares o extensiones lineales paralelas, y permiten la creación de un trapecio arbitrario. Este trapecio aún estará biseccionado, y la suma de los cuadrados en los lados paralelos seguirá siendo el doble de la transversal paralela.
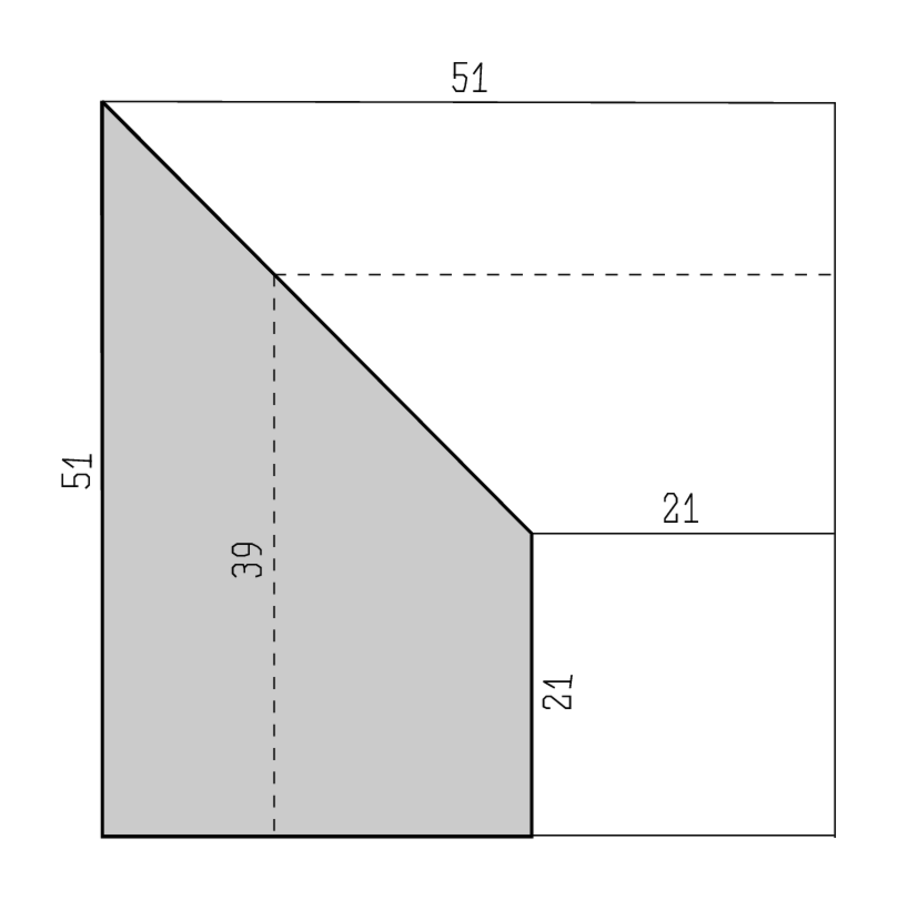
Podemos tomar nota de que la operación de “dibujar largo” es la misma que el cambio de escala en una dirección que hemos encontrado en la solución de problemas no normalizados, y que también se utilizó en TMS XIII, el comercio petrolero (ver página 70); volveremos a encontrarla en un momento en el presente problema.
Posiblemente la regla se encontró por primera vez sobre la base de cuadrados concéntricos (Figura 5.3) —la configuración geométrica representada por dos o varios cuadrados anidados concéntricamente fue muy apreciada en las matemáticas babilónicas y puede haber sido así ya en el tercer milenio (como quedó popular entre los maestros constructores hasta el Renacimiento); el principio del argumento evidentemente sigue siendo el mismo.
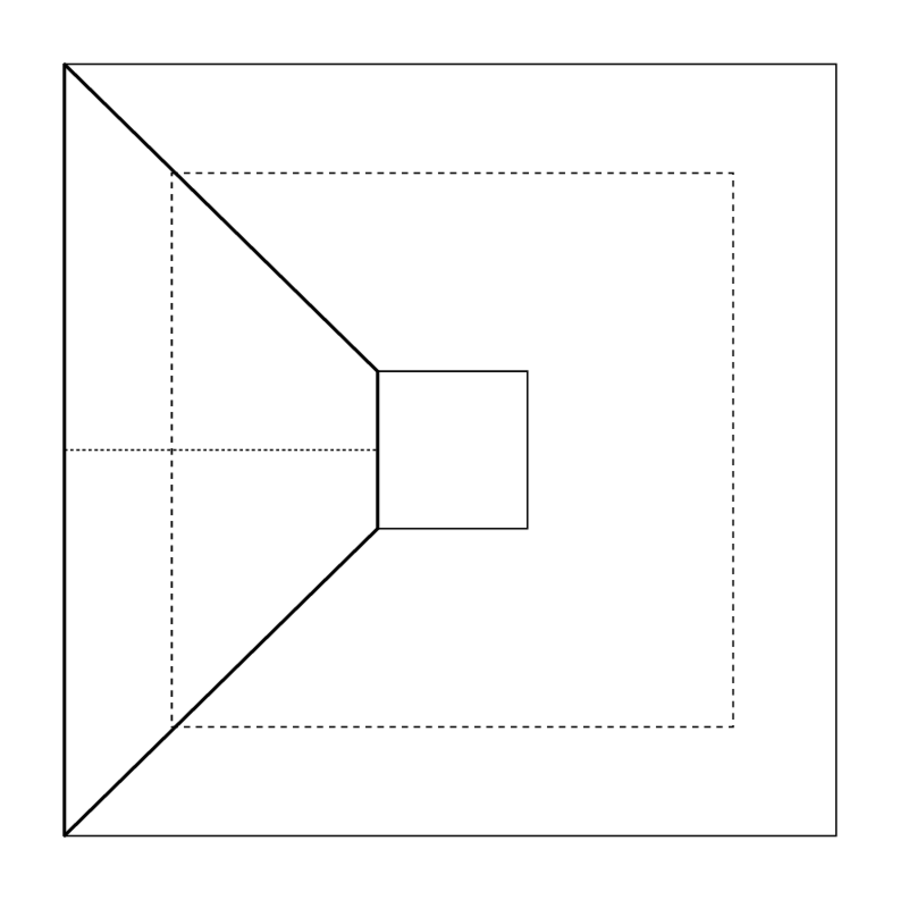
La línea Obv. 17 encuentra así la bisección transversal; resulta ser\(39\), y la “barra” entre las dos parcelas originales debe ser por lo tanto\(39-21=18\).
Los siguientes pasos pueden parecer extraños. Las líneas Obv. 21-22 aparecen para calcular el ancho del triángulo, pero esta fue una de las magnitudes dadas del problema. esto significa sin duda que efectivamente hemos dejado atrás la Figura 5.1, y que el argumento ahora se basa en algo así como la Figura 5.2. Cuando eliminamos el ancho adicional 21 nos quedamos con un triángulo que corresponde al triángulo inicial pero que es isósceles—Figura 5.4.
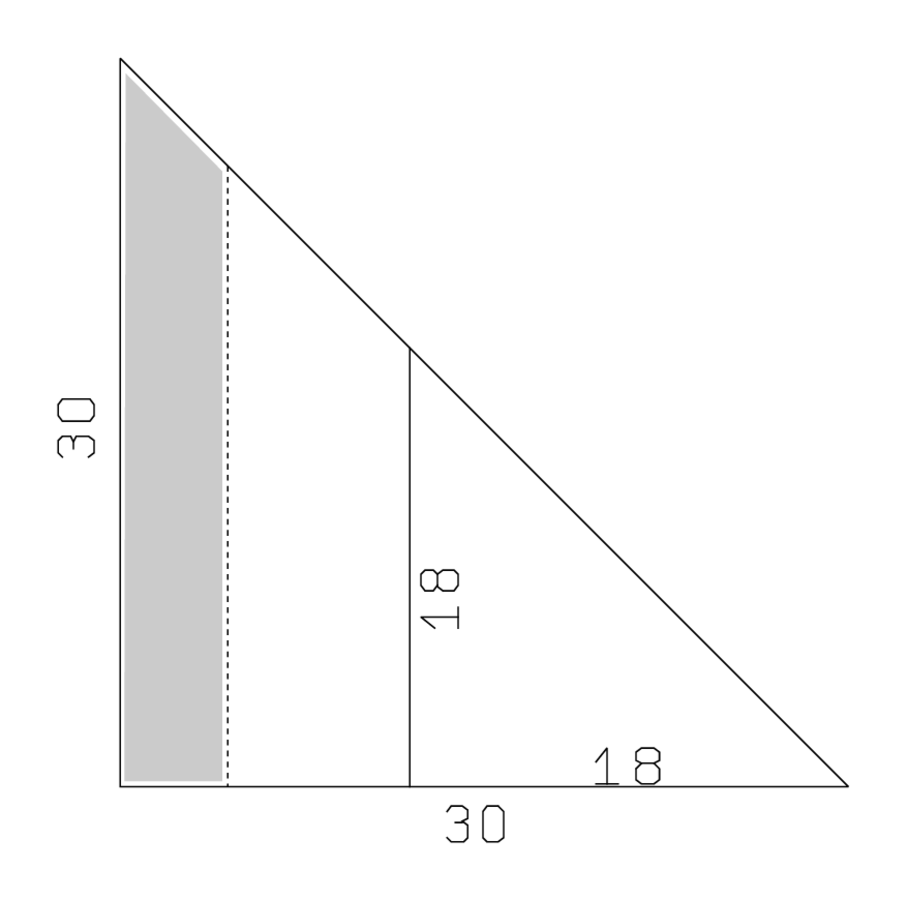
Para encontrar al “descendiente superior” el texto hace la falsa posición de que el triángulo acortado e isósceles es el que estamos buscando. Su longitud (la suma de los “descendientes”) es entonces igual al ancho, es decir, a\(30\). Para encontrar el verdadero triángulo tendremos que cambiar la escala en la dirección de la longitud.
Líneas Obv. 23-24 calculan que el área del falso triángulo es\(7`30\). Las dos áreas en blanco son iguales, y su suma debe ser\(2 \cdot\left(\frac{1}{2} \cdot(18 \cdot 18)\right)=5` 24\). Por lo tanto, el área sombreada, que corresponde a la diferencia entre las dos parcelas, debe ser\(7` 30-5` 24=2` 6\) (borde 1-3).
Pero sabemos que la diferencia es\(7`\) y no\(2`6\). Por lo tanto, las líneas Rev. 1-3 establecen\(2`6\) que la diferencia que resulta de la falsa posición debe multiplicarse por\(3^{\circ} 20^{\prime}\) si queremos encontrar la verdadera diferencia\(7`\). Dado que el wdith ya es lo que debería ser, es la longitud y los “descendientes” los que deben multiplicarse por este factor. El “descendiente superior” será así\(3^{\circ} 20^{\prime} \cdot(30-18)=40\) (línea Rev. 6). Después todo es bastante sencillo; podría haber sido aún más sencillo, pero el camino que se elige concuerda mejor con el estilo pedagógico que conocemos por ejemplo de TMS XVI #1, y probablemente sea más fructífero desde un punto de vista didáctico.
La forma en que se resuelve este problema ciertamente difiere de lo que hemos encontrado hasta ahora. Pero también hay características comunes que se vuelven más llamativas a vista de pájaro.
El cambio de escala en una dirección que ya conocemos como técnica algebraica. Una diferencia no menos conspicua —la ausencia de una terminación cuadrática, es decir, del “método acadio” —apunta a otra característica familiar: la introducción de una figura auxiliar que primero se “une” y luego “arranca”.
Menos evidente pero fundamental es el carácter “analítico” de los métodos. Desde la antigüedad griega, la solución de un problema matemático se llama “analítica” si parte del supuesto de que el problema ya está resuelto; eso nos permite examinar —"analizar” —las características de la solución para entender cómo construirla. 1
Una solución por ecuación es siempre analítica. Para entender que podemos volver a mirar nuestra solución moderna de TMS XIII, el comercio petrolero (página 70). Según la hipótesis de partida, la cantidad de sìla que se compra por 1 shekel de plata es un número conocido, y nosotros lo llamamos\(a\). Hacemos lo mismo con la tasa de ventas (a la que llamamos\(v\)). La inversión total es de ahí\(M \div a\), el precio total de venta\(M \div v\), y el beneficio por lo tanto\(w=\frac{M}{v}-\frac{M}{a}\). Entonces nos multiplicamos por\(v \times a\), y así sucesivamente.
Es decir, tratamos\(a\) y\(v\) como si fueran números conocidos; pretendemos tener una solución y describimos sus características. Después derivamos las consecuencias—y encontramos al final que\(a=11\),\(v=7\).
Incluso las soluciones de corte y pasta de Old Babilonian son analíticas. Presuponiendo que conocemos una solución al problema petrolero lo expresamos como rectángulo de área\(12`50\), del cual una parte de longitud\(40\) corresponde a la ganancia petrolera. Luego examinamos las características de esta solución, y encontramos el factor de normalización por el cual debemos multiplicar para obtener una diferencia 4 entre los lados, y así sucesivamente.
La solución al problema actual también es analítica. Presuponemos que el triángulo ha sido completado por un rectángulo de tal manera que la “barra” prolongada divide el trapecio resultante en partes iguales, después de lo cual calculamos cuánto debe ser el ancho del rectángulo si ese será el caso; y así sucesivamente. A pesar de que tiene su justificación, la distinción entre “álgebra” (Problemas que se traducen fácilmente en ecuaciones modernas) y “cuasiálgebra” parece menos importante en la perspectiva de los textos babilónicos antiguos que en la nuestra.