5.2: BM85200 + IVA 6599 #6

Última actualización
Guardar como PDF

Page ID: 109627

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Obv. I

9 Una excavación. Tanto como la longitud, esa es la profundidad. 1 la suciedad que he arrancado. Mi suelo y la suciedad que he colmado,\(1^{\circ} 10^{\prime}\). Largo y ancho,\(50^{\prime}\). Largo, ancho, ¿qué?

10 Tú,\(50^{\prime}\) a 1, la conversión,\(50^{\prime}\) levantas, ya ves. \(50^{\prime}\)a 12 subir, 10 ya ves.

11 Hacer\(50^{\prime}\) confrontarse a sí mismo,\(41^{\prime} 40^{\prime \prime}\) ya ve; a 10 subir,\(6^{\circ} 56^{\prime} 40^{\prime \prime}\) ya ve. Su igi se desprenden,\(8^{\prime} 38^{\prime \prime} 24^{\prime \prime \prime}\) ya ves;

12 para\(1^{\circ} 10^{\prime}\) subir,\(10^{\prime} 4^{\prime \prime} 48^{\prime \prime \prime}\) ya ves,\(36^{\prime}\),\(24^{\prime}\),\(42^{\prime}\) son iguales.

13\(36^{\prime}\) para\(50^{\prime}\) levantar,\(30^{\prime}\), la longitud. \(24^{\prime}\)para\(50^{\prime}\) elevar,\(20^{\prime}\), el ancho;\(36^{\prime}\) a 10 subir, 6, la profundidad.

14 El trámite.

Se trata de un problema de tercer grado, proveniente de una tableta que se ha dividido en dos partes, una de las cuales está en Londres y otra en Berlín (de ahí el nombre compuesto). Se trata de una “excavación” paralelepipédica, de longitud\(\ell\) [\(\mathrm{NINDAN}\)], anchura\(w\) [\(\mathrm{NINDAN}\)] y profundidad\(d\) [\(mathrm{kùš}]. The length is equal to the depth, but because of the use of different metrologies in the two directions that means that \(d=12 \ell\).

Figura\(5.5\): La excavación se extendió 1 kùš hacia abajo.

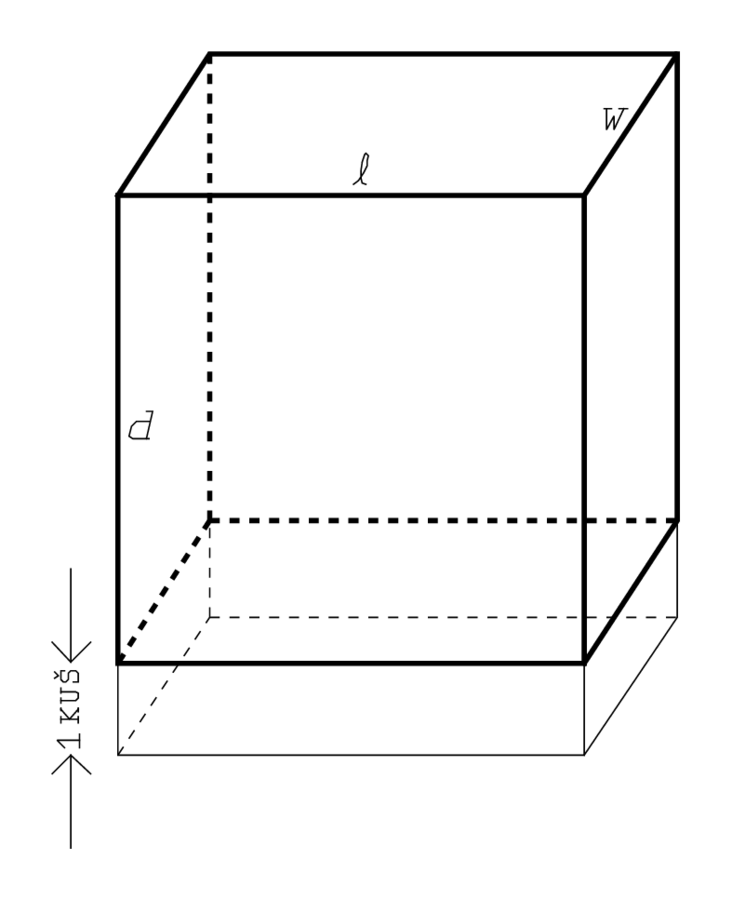
Además la suma de la longitud y la anchura es\([\ell+w=]\)\(50^{\prime}\), y la suma del volumen de suciedad que se ha “arrancado”, es decir, excavado ² y el “suelo” (la base) es\([\ell \cdot w \cdot d+\ell \cdot w=]\)\(1^{\circ}10^{\prime}\). Esta última ecuación se puede transformar en\(\ell \cdot w \cdot(d+1)=1^{\circ} 10^{\prime}\) —es decir, si la excavación se hubiera cavado 1 kùš más profundo, su volumen habría igualado\(1^{\circ}10^{\prime}\) [\(\mathrm{NINDAN}^{2} \cdot \mathrm{kùš}\)] (Figura 5.5). ³

La solución se basa en una variante sutil de la posición falsa (en su forma apropiada este método no serviría, ya que el problema no es homogéneo —ver nota 7, página 50). “La posición” consiste en la construcción de un “cubo de referencia” con el lateral\(\ell + w\). En medida horizontal, su lado es\(1 \cdot 50^{\prime}=50^{\prime}\) [\(\mathrm{NINDAN}\), ya que “la conversión” de\(\mathrm{NINDAN}\) pide una multiplicación por 1. En medida vertical, es\(12 \cdot 50^{\prime}=10\) kùš, ya que “la conversión” de\(\mathrm{NINDAN}\) en kùš implica una multiplicación por 12 (ambas conversiones tienen lugar en la línea 10).

Las líneas 11-12 encuentran el volumen del cubo de referencia a ser\(6^{\circ} 56^{\prime} 40^{\prime \prime}\). Este volumen está contenido en\(10^{\prime} 4^{\prime \prime} 48^{\prime \prime \prime}\) tiempos en la excavación extendida.

Ahora debemos imaginar que los lados de la excavación extendida se miden por los lados correspondientes del cubo de referencia. Si\(p\) es el número de veces que\(\ell\) se mide la longitud\(50^{\prime} \mathrm{NINDAN}\),\(q\) el número de veces que\(w\) se mide el ancho y\(r\) el número de veces que la profundidad\(d+1\) kùš se mide por\(10\) kùš (\(=50^{\prime} \mathrm{NINDAN}\)), entonces\(50^{\prime} \mathrm{NINDAN}\)

\(p \cdot 50^{\prime}+q \cdot 50^{\prime}=\ell+w=50^{\prime}\),

y por lo tanto

\(p + q =1\);

además

\(r \cdot 10=d+1=12 \ell+1=12 \cdot p \cdot 50^{\prime}+1=10 p+1\)

de donde

\(r=p+\frac{1}{10}=p+6^{\prime}\)

y finalmente

\(p \cdot q \cdot r=10^{\prime} 4^{\prime \prime} 48^{\prime \prime \prime}\)

Por lo tanto, tenemos que expresarnos\(10^{\prime} 4^{\prime \prime} 48^{\prime \prime \prime}\) como producto de tres factores\(p\),\(q\) y\(r\) que fulfiil estas condiciones. Eso es lo que hace el texto en la línea 12, wehre los factores aparecen como los “iguales”\(36^{\prime}\),\(24^{\prime}\) y\(42^{\prime}\). Después, la línea 13 encuentra\(\ell\),\(w\) y\(d\).

La factorización parece estar extraída de las mangas del maestro-mago, y probablemente así es como se ha producido realmente, al igual que las diversas raíces cuadradas y cocientes. Dado que la solución se conocía de antemano, eso sería fácil. pero también es posible encontrarla por razonamiento systematci, comenzando con números simples, uno solo debe expresar\(10``4`48\) (\(=2^{6} \cdot 3^{4} \cdot 7\)) como producto de tres números\(P\),\(Q\) y\(R\) dónde\(P + Q = 60\),\(R = P + 6\). ⁴ Conociendo el carácter general de las matemáticas babilónicas antiguas podemos incluso afirmar que el texto sólo puede permitirse sacar la respuesta de las mangas porque sería posible (aunque algo laborioso) encontrarla sin magia. Supongamos primero que\(P = 1\); entonces, ya que\(P + Q = 60\),\(Q\) será\(59\), lo que es imposible; las hipótesis\(P = 2\) y\(P = 3\) pueden ser rechazadas por razones análogas;\(P = 4\) da\(R = 10\), que también se excluye— no\(10``4`48\) contiene factor 5;\(P = 5\) es imposible en sí mismo;\(P = 6\) da\(Q = 54\) y\(R = 12\), que debe ser rechazada, tanto porque falta el factor 7 como porque el control muestra que el producto no es lo que son las mismas razones;\(P = 18\) es imposible porque el producto es sólo alrededor de la mitad de lo que se necesita. \(P = 24\)y\(P = 30\) deberá ser rechazada por las mismas razones que\(P = 6\). Finalmente llegamos a\(P = 36\), un valor que encaja. Si hubiéramos contado factores primos hubiera sido aún más fácil, pero nada sugiere que los babilonios conocieran esa técnica.

Debe enfatizarse, sin embargo, que este método sólo funciona porque existe una solución simple. De este modo, el problema difiere fundamentalmente de los de segundo grado, donde una buena aproximación a lo que “es igual” daría una solución casi correcta (y los babilonios no fueron capaces de resolver problemas cúbicos en general ya que podían resolver problemas de segundo grado, para eso, había que esperar el algebraista italiano del siglo XVI a.C.

Nuestro texto habla de tres “iguales” que ni siquiera son iguales. Este uso evidentemente representa una generalización de una idea que viene de los lados del cuadrado y del cubo no hay nada extraño en tal generalización: nuestra propia noción de las “raíces” de una ecuación viene de la misma manera desde álgebra árabe temprana, donde las ecuaciones fundatmentales se formularon en términos de una cantidad de dinero y su raíz cuadrada. Al olvidarse este origen la palabra llegó a entenderse como una designación para el valor de lo desconocido que satisface la ecuación.

Otros problemas de la misma tablilla hablan de un solo “igual”; es el caso cuando el volumen de la excavación medido por el paralelepípedo de referencia (no siempre un cubo) debe factorizarse como\(p^{3}\) o como\(p^{2} \cdot(p+1)\). Efectivamente existen tablas para estos dos funcitones, y en estos\(p\) aparece precisamente como “el igual”; esta última tabla tenía el nombre “igual, 1 unido"—ver página 126.

Al igual que en el álgebra de segundo grado, el tratamiento de los problemas de tercer grado es analítico, lo que acabamos de ver es un representante típico de la categoría: uno presupone que existe una solución y extrae las consecuencias de lo que se puede afirmar. De la misma manera, toda solución por medio de una posición falsa es analítica, comienza por la hipótesis de una solución.

Aparte de eso, solo características bastante periféricas conectan el segundo y tercer grado: la terminología para las operaciones, el uso de tablas, las operaciones aritméticas fundamentales.

Otros problemas en la misma tableta (todos los que se ocupan de “excavaciones” paralelepipédicas) se reducen a problemas de segundo o incluso primer grado. Estos se resuelven con las técnicas que ya conocemos, y nunca por factorización. Los babilonios eran así conscientes de poseer otra (y en su opinión, como vemos) mejor técnica, y conocían perfectamente la diferencia entre los problemas que pueden resolverse con sus técnicas algebraicas y los que no ceden a tales ataques. Pero parecen no haber visto esta diferencia entre problemas que pueden resolverse con sus técnicas algebraicas y los que no ceden a tales ataques. pero parecen no haber visto esta diferencia como fundamental —el género matemático que se define por el contenido de la tablilla es más bien “excavación” problemas”, así como el género definido por BM 13901 debe entenderse como “problemas cuadrados” a pesar de que uno de los problemas se reduce a un problema de rectángulo. Una vez más, la distinción entre “álgebra” y “cuasiálgebra” parece ser secundaria, menos importante que la clasificación de los problemas según el objeto que consideren.