6.1: ¿Dibujos?

Todos los textos que se discutieron anteriormente fueron ilustrados por dibujos geométricos. Sin embargo, sólo dos de las tablillas llevaban diagramas geométricos, y en ambos casos estos ilustraban la afirmación del problema, no el procedimiento.

Muchos aspectos de los procedimientos son inexplicables en la interpretación aritmética tradicional pero naturalmente explicados en una lectura geométrica. en consecuencia, algún tipo de geometría debe haber participado en el razonamiento de los babilonios. No es muy plausible, sin embargo, que los babilonios hicieron uso de dibujos tranquilos como el nuestro. Por el contrario, muchos textos nos dan razones para creer que estaban estigmatizados con diagramas de estructura rudimentarios; véase por ejemplo la página 52 sobre el cambio de escala en una dirección. La ausencia de nombres particulares para\(L = 3\lambda\) y\(W = 21\phi\) en TMS IX #3 (ver página 59) también sugiere que no se creó ningún nuevo diagrama en el que pudieran identificarse, mientras que\(\lambda\) y\(\phi\) podrían identificarse como lados de la “superficie 2".

Después de todo, eso no es de extrañar. Quien esté familiarizado con las técnicas babilónicas antiguas no necesitará más que un boceto rudo para seguir el razonamiento; ni siquiera hay necesidad de realizar las divisiones y desplazamientos, el dibujo del rectángulo por sí solo permite captar el procedimiento a utilizar. de la misma manera que podemos realizar un cálculo mental, haciendo como máximo notas para uno o dos resultados intermedios, también podemos familiarizarnos con la “geometría mental”, a lo sumo asistido por un diagrama áspero.

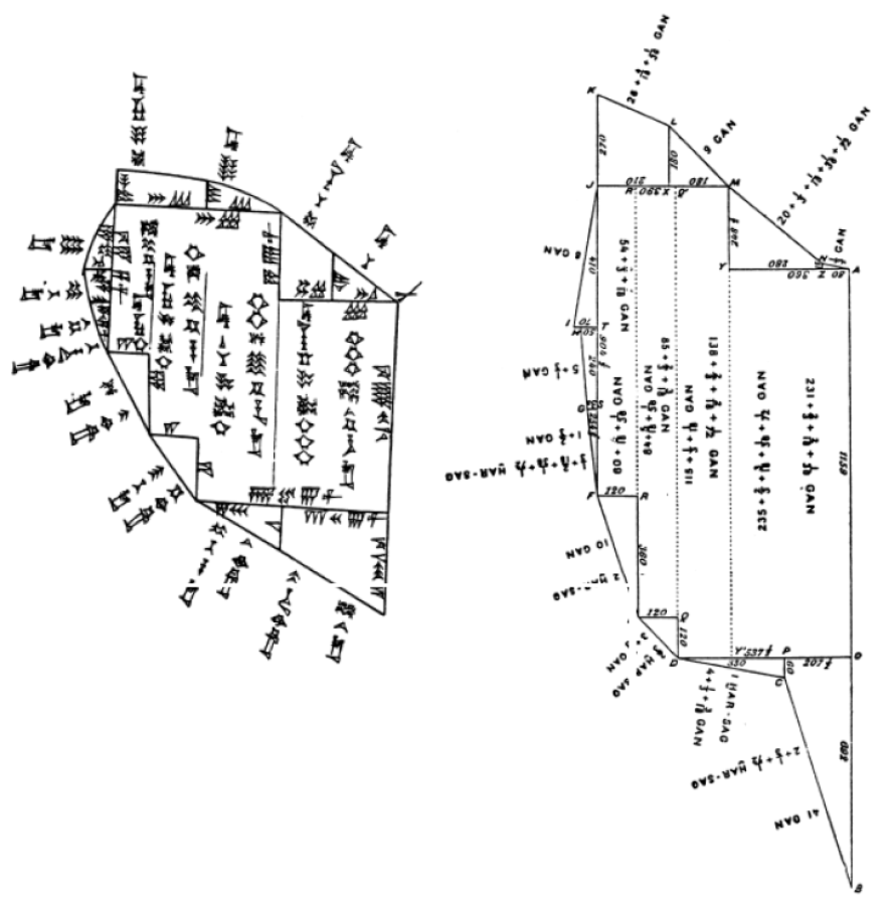
Un buen número de planos de campo realizados por escribas mesopotámicos han sobrevivido; la parte izquierda de la Figura 6.1 muestra uno de ellos. Tienen precisamente el carácter de diagramas de estructura; no pretenden ser fieles en la renderización de proporciones lineales, como se verá si comparamos con la versión en proporciones correctas a la derecha. En ese sentido son similares a la Figura 4.5, cuyas verdaderas proporciones se pueden ver en la Figura 4.6 — páginas 65 y 68, respectivamente. Tampoco les interesa mostrar ángulos correctamente, aparte de los ángulos “prácticamente rectos” que sirven a los cálculos de área y por lo tanto tienen un papel estructural.

Figura\(6.1\): Un plano de campo neosumerio (siglo XXI a. C.), dejado como dibujado en la tablilla, redibujado a la derecha en proporciones correctas Después de F. Thureau-Dangin, “Un catastro chaldéen”. Revue d'Assyriologie 4 (1897—98), 13—27.

Practicar la “geometría mental” presupone que se ha entrenado primero la geometría del concreto; así, deben haber existido dibujos reales de algún tipo. Sin embargo, las operaciones de cortar y pegar no se realizan fácilmente en una tableta de arcilla. El ábaco de polvo, utilizado por las calculadoras fenicias en el primer milenio antes de Cristo y luego tomado por los geometros griegos, ¹ es mucho más conveniente para este propósito. Aquí es fácil cancelar una parte de una figura y volver a dibujarla en una nueva posición. También sería conveniente un patio escolar sembrado de arena (cf. página 33).

De la misma manera, el polvo o la arena parecen haber servido en los primeros pasos del aprendizaje del guión. A partir de esta fase inicial, se conocen las tablillas en las que se inscriben los modelos que se supone que han reproducido los alumnos para aprender los personajes cuneiformes. De la siguiente fase también tenemos las tablillas de arcilla escritas por los estudiantes, pero desde la primera fase el trabajo de los estudiantes no ha dejado huellas arqueológicas, lo que significa que probablemente éstas habrán sido dibujadas en arena o polvo. Por lo tanto, no hay razón para asombrarse de que no se hayan encontrado los dibujos geométricos de la enseñanza del álgebra y la cuasiálgebra.