10.1: Apéndice A- Problemas para el Lector

Los problemas presentados en los Capítulos 2 — 5 eran tan diferentes uno de los demás que fue necesario acompañar a cada uno de ellos con un copioso comentario. Con el fin de permitir al lector que quiera explorar algunos textos babilónicos antiguos sin ser sostenido firmemente de la mano, este apéndice contiene problemas en la traducción únicamente, o a lo sumo acompañados de las aclaraciones más necesarias. Algunas son contrapartes de problemas que se presentaron anteriormente y provienen de las mismas tabletas.

TMS XVI #2

13 El 4to de la anchura a aquella por la que la longitud va más allá de la anchura, para unir,

14\(15^{\prime}\). Tú,\(15^{\prime}\) a 4 subir, 1 ya ves, ¿qué es?

15 4 y 1 postulación.

16\(15^{\prime}\) dispersión. \(10^{\prime}\), el ir más allá, y\(5^{\prime}\), el unido, postular. \(20^{\prime}\), la anchura,

17 a\(10^{\prime}\), el ir más allá, unir,\(30^{\prime}\) la longitud, y\(20^{\prime}\), para arrancar, postular. \(5^{\prime}\)a 4 elevar,

18\(20^{\prime}\) ya ves. \(20^{\prime}\), el ancho, a 4 subir,\(1^{\circ} 20^{\prime}\) ya ves.

19\(30^{\prime}\), la longitud, a 4 subir, 2 ya ves. \(20^{\prime}\), la anchura,

20 de\(1^{\circ} 20^{\prime}\) arrancar, 1 ya ves. 1

21 de 2, los largos, arrancan, 1 ya ves, ¿qué es?

22 De 4, de la cuarta, 1 arranca, 3 ves. igi 4 desprenderse,\(15^{\prime}\) ya ves.

23\(15^{\prime}\) a 3 subir, ya\(45^{\prime}\) ves, tanto como (hay) de anchuras postulan. Postura para arrancar.

24 1 tanto como (hay) de longitudes postular. [...] 1 toma, a 1 longitud

25 subir,\(30^{\prime}\) ya ves. \(20^{\prime}\)el ancho,\(20^{\prime}\) a\(45^{\prime}\), (tanto como (hay) de) anchos, subir,

26\(15^{\prime}\) ves,\(15^{\prime}\) para\(15^{\prime}\) unirte,\(30^{\prime}\) ya ves, 30 la longitud.

Comentario: ver #1 de la misma tablilla, página 27.

TMS VII #1

1 El 4to del ancho al largo que me he unido, su 7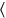 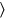a 10 me he ido,

2 tanto como el montón de largo y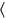 ancho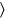. Tú, 4 posit; 7 posit;

3 10 postular;\(5^{\prime}\) a 7 subir, 35′ ya ves.

4\(30^{\prime}\) y\(5^{\prime}\) singular. \(5^{\prime}\), el escalón, a 10 levantar,

5\(50^{\prime}\) ya ves. \(30^{\prime}\)y\(20^{\prime}\), postular. \(5^{\prime}\), el escalón, a 4, del cuarto de la anchura,

6 subir:\(20^{\prime}\) ya ves,\(20^{\prime}\), el ancho. \(30^{\prime}\)a 4, de la cuarta,

7 subir, 2 ya ves. 2 postular, longitudes. \(20^{\prime}\)de\(20^{\prime}\) arrancar,

8 y de 2,\(30^{\prime}\) arranca,\(1^{\circ} 30^{\prime}\) ya ves.

9 De 4, de la cuarta, 1 arranca, 3 {...} ya ves.

10 igi 3 desprenderse,\(20^{\prime}\) ya ve. \(20^{\prime}\)para\(1^{\circ} 30^{\prime}\) plantear:

11\(30^{\prime}\) ya ves,\(30^{\prime}\) la longitud. \(30^{\prime}\)de\(50^{\prime}\) arrancar,\(20^{\prime}\) ya ves,\(20^{\prime}\) el ancho.

12 Da la vuelta. 7 a 4, del cuarto, subir, 28 ya ves.

13 10 de 28 arrancar, 18 ya vees. igi 3 desprender,

14\(20^{\prime}\) ya ves. \(20^{\prime}\)a 18 subir, 6 ves, 6 (para) la longitud.

15 6 de 10 arrancan, 4 (para) el ancho. \(5^{\prime}\)a 6 elevar,

16\(30^{\prime}\) la longitud. \(5^{\prime}\)a 4 subir,\(20^{\prime}\) ya ves,\(20^{\prime}\) el ancho.

Comentario: ver #2 de la misma tablilla, página 34.

IVA 8389 #1

Obv. I

1 De 1 bùr 4 gur de grano que he recogido,

2 de 1 segundo bùr 3 gur de grano que he recogido.

3 grano sobre grano,\(8‵20\) fue más allá

4 Mis parcelas las he acumulado:\(30‵\).

5 Mis parcelas ¿qué?

6\(30‵\), el bùr, postular. \(20‵\), el grano que ha recogido, postula.

7\(30‵\), el segundo bùr, postular.

8\(15‵\), el grano que ha recogido,

9\(8‵20\) que el grano sobre el grano fue más allá,

10 y\(30‵\) la acumulación de las superficies de las parcelas postula:

11\(30‵\) la acumulación de las superficies de las parcelas

Descanso de 12 a dos:\(15‵\).

13\(15‵\) y\(15‵\) hasta dos veces postular:

14 igi\(30‵\), del bùr, desprender:\(2^{\prime \prime}\).

15\(2^{\prime \prime}\) a\(20‵\), el grano que ha recogido,

16 subir,\(40^{\prime}\) el grano falso; a\(15‵\) lo que hasta dos veces

17 que has postergado,

18 subir, ¡\(10‵\)que te sostenga la cabeza!

19 igi 30, del segundo bùr, desprender,\(2^{\prime \prime}\).

20\(2^{\prime \prime}\) a\(15‵\), el grano que ha recogido,

21 levantar,\(30^{\prime}\) el grano falso; a 15 que hasta dos veces

22 has postpuesto, subir,\(7‵30\).

23\(10‵\) que sostiene tu cabeza

24 sobre\(7‵30\) lo que va más allá? \(2‵30\)va más allá.

25\(2‵30\) que va más allá, de\(8‵20\)

26 que el grano sobre el grano va más allá,

Obv. II

1 arranca:\(5‵50\) te vas.

2\(5‵50\) que te queda

3 que tu cabeza sostenga!

4\(40^{\prime}\), el cambio, y\(30^{\prime}\), el cambio,

5 acumulan:\(1^{\circ} 10^{\prime}\). El igi no lo sé.

6 Qué\(1^{\circ} 10^{\prime}\) puedo postular

7\(5‵50\) que me da tu cabeza?

8\(5‵\) postular. \(5‵\)a 1°10 subir.

9\(5‵50\) te da.

10\(5‵\) que has postulado, de los\(15‵\) cuales hasta dos veces

11 has postpuesto, de una lágrima,

12 a uno se unen:

13 El primero es\(20‵\), el segundo es\(10‵\).

14\(20‵\) (es) la superficie de la primera parcela,\(10‵\) (es) la superficie de la segunda parcela.

15 Si\(20‵\) (es) la superficie de la primera parcela,

16\(10‵\) la superficie de la segunda parcela, sus granos ¿qué?

17 igi\(30‵\), del bùr, desprender:\(2^{\prime \prime}\).

18\(2^{\prime \prime}\) a\(20‵\), el grano que ha recogido,

19 elevar,\(40^{\prime}\). A\(20‵\), la superficie de la primera parcela,

20 elevar,\(13‵20\) el grano de\(20‵\), la superficie de la parcela.

21 igi\(30‵\), del segundo bùr, desprender:\(2^{\prime \prime}\).

22\(2^{\prime \prime}\) a\(15‵\), el grano que ha recogido, levantar,\(30^{\prime}\).

23\(30^{\prime}\) a\(10‵\), la superficie de la segunda parcela

24 elevar, 5 el grano de la superficie de la segunda parcela.

25\(13‵30\) el grano de ^¿la superficie^? de la primera parcela

26 sobre 5 el grano de ^¿la superficie^? de la segunda parcela

27 ¿qué va más allá? \(8‵20\)va más allá.

Este problema pertenece a una de las dos tabletas gemelas, que contiene un total de diez problemas sobre la renta pagada por dos paquetes de un campo. En una parcela la renta es de 4 gur de grano por bùr, en la otra es de 3 gur por bùr. El presente problema nos informa también que la superficie total es\(30`\) (sar = 1 bùr), y que la diferencia entre las rentas totales de las dos parcelas es\(8`20\) (sìla). Los otros problemas dan, por ejemplo, las dos áreas, o la diferencia entre las áreas junto con la renta total.

Como se explica en la página 17, el bùr y el gur son unidades pertenecientes a la vida práctica. Para trabajar en el sistema de valor posicional necesitamos convertirlas en las unidades estándar sar y sìla (1 bùr =\(30‵\) sar, 1 gur =\(5‵\) sìla); como vemos, la diferencia entre las dos rentas ya se da en sìla, y la superficie total en sar.

A un lector moderno puede resultarle extraño que las dos rentas por bùr, que en las líneas I. 1-2 se dan en gur (per bùr), se traduzcan a sìla en líneas I. 6-7 sin multiplicación; en general, como vemos, el texto no salta ningún paso intermedio. La explicación es que la conversión se realiza por medio de una “tabla metrológica” (probablemente una tabla aprendida de memoria). Precisamente porque tales conversiones tenían que hacerse con tanta frecuencia, los escribas tenían tablas que no sólo expresaban los valores convertidos de las unidades prácticas sino también de sus múltiplos. Sin embargo, no tenían tablas para conversiones combinadas, por lo que la conversión final a sìla per sar pide cálculo.

El lector moderno también puede preguntarse que el texto no indique de una vez por todas el valor del bùr per sìla y su igi. Una vez más la razón es que el texto describe la técnica calculacional babilónica antigua: la calculadora escribe en una pequeña tablilla para trabajo aproximado los tres números 20 (\(20`\)sìla per bùr), 30 (\(30``\)sar per bùr) y 2 (\(2^{\prime}\), igi\(30`\) —y posteriormente, por medio de la tabla de multiplicación , el producto 40 (\(20`\cdot 2^{\prime \prime}=40^{\prime}\)sìla per sar).

Puede ser necesaria una pequeña explicación para facilitar la comprensión del procedimiento: primero el texto determina cuál sería la diferencia entre las dos rentas si las dos parcelas hubieran sido iguales en superficie, es decir,\(15`\) sar cada una. Esta diferencia no es lo bastante grande —es\(2`30\) sìla,\(5`50\) sìla demasiado pequeña— y por lo tanto la primera parcela debe ser agrandada. Cada vez que se transfiere un sar de la segunda a la primera parcela, la diferencia crece por\(40^{\prime}+30^{\prime}\) sìla (los dos “cambios” de II.4 ¹); el número de sar que debe transferirse se encuentra entonces por división.

Al final encontramos una verificación numérica. Tales verificaciones no son raras en los textos babilónicos antiguos a pesar de que su presencia no es una norma general.

IVA 8390 #1

Obv. I

1 Largo y ancho que he hecho sujetar:\(10‵\) la superficie.

2 La longitud a sí misma la he hecho sostener:

3 una superficie que he construido.

4 Tanto como la longitud sobre el ancho fue más allá

5 he hecho bodega, a 9 he repetido:

6 tanto como esa superficie que la longitud por sí misma

7 se hizo bodega.

8 El largo y el ancho ¿qué?

9\(10‵\) la posición de la superficie,

10 y 9 (a) que ha repetido postula:

11 El igualado de 9 (a) que ha repetido ¿qué? 3.

12 3 a la posición de longitud

13 3 a la posición de ancho.

14 Ya que “tanto como la longitud sobre el ancho fue más allá

15 he hecho bodega”, ha dicho

16 1 de 3 que a la anchura que has postergado

17 arrancan: 2 te vas.

18 2 que le ha dejado a la posición de ancho.

19 3 que a la longitud que has postergado

20 a 2 que al ancho que has postulado subir, 6.

21 igi 6 desprender:\(10^{\prime}\).

22\(10^{\prime}\) a\(10‵\) la superficie subir,\(1‵40\).

23 ¿El igual de\(1‵40\) qué? 10.

Obv. II

1 10 a 3 que a la longitud que has postergado

2 subir, 30 la longitud.

3 10 a 2 que al ancho que has postergado

4 subir, 20 el ancho.

5 Si 30 el largo, 20 el ancho,

6 la superficie ¿qué?

7 30 la longitud a 20 el ancho subir,\(10‵\) la superficie.

8 30 la longitud junto con 30 hacen que sostenga:\(15‵\).

9 30 la longitud sobre 20 el ancho ¿qué va más allá? 10 va más allá.

10 10 junto con 10 hacen sujeción:\(1‵40\).

11\(1‵40\) a 9 repetir:\(15‵\) la superficie.

12\(15‵\) la superficie, tanto como\(15‵\) la superficie que la longitud

13 por sí mismo se hizo aferrarse.

Como soporte para la interpretación, puede servir un diagrama (Figura 1). Entonces el texto casi se explica a sí mismo, en particular si se tiene en cuenta BM 13901 #10 (página 46) y BM 15285 #24 (página 93).

Figura\(1\): La geometría del IVA 8390 #1.

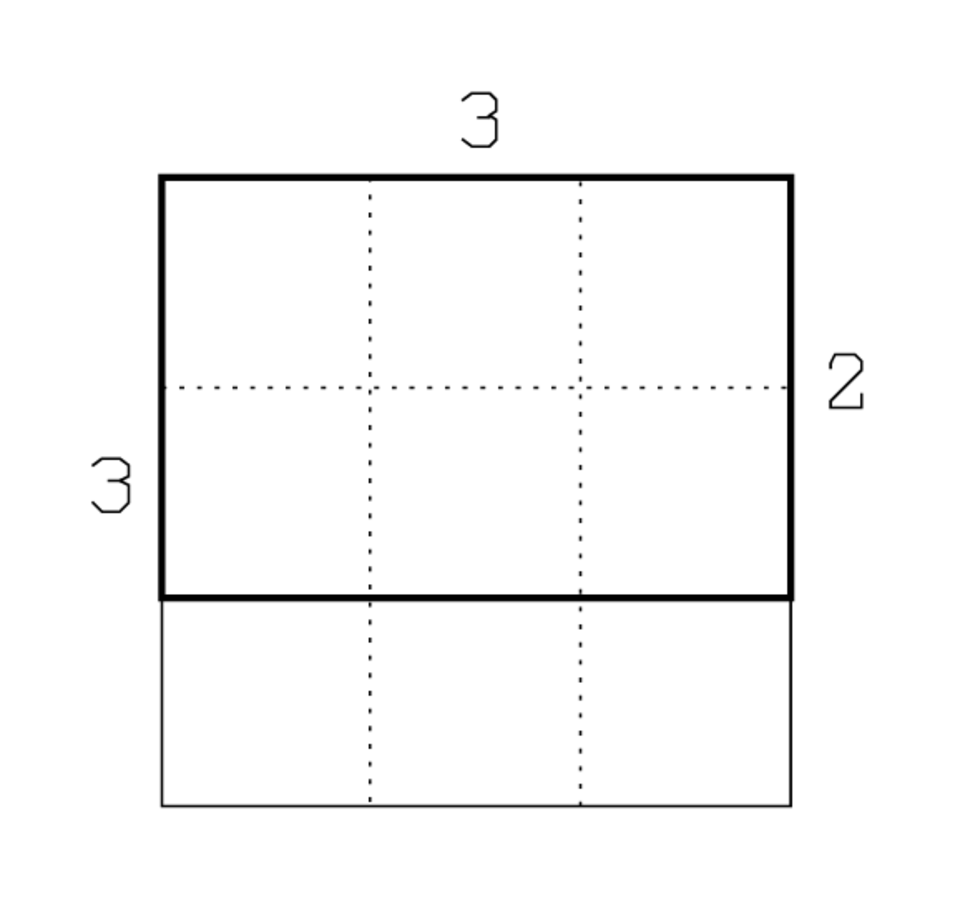
Se debe tomar nota del uso de las operaciones multiplicativas “make hold”, “raise” y “repeat”. Que “afianzar” realmente implica que una construcción está subrayada en I.3, como también hemos visto en AO 8862 #2 (página 60). El “levantamiento” en I. 20 y II. 7 es de especial interés: encuentra el área de rectángulos, pero como estos ya están en su lugar, no hay necesidad de construirlos. Por lo tanto, el área es meramente calculada.

IVA 8520 #1

Obv.

1 El 13 del montón del igûm y el igibûm

2 a 6 he repetido, desde el interior del igûm

3 He arrancado:\(30^{\prime}\) me queda. 1 la superficie. El igûm y el igibûm ¿qué?

4 Desde “el decimotercer del montón del igûm y el igibûm

5 a 6 he repetido, desde el interior del igûm

6 He arrancado:\(30^{\prime}\) me he ido”, ha dicho,

7 13, de la decimotercera, postular; 6 a lo que ha repetido postular;

8 1, la superficie, postular; y\(30^{\prime}\) que ha dejado postular.

9 Del 13, del decimotercero, 6 a lo que ha repetido

10 arrancan. 7 te vas.

11 7 que dejas y 6 a las que has repetido,

12 ¡Que tu cabeza sostenga!

13 7 a 6 subir, 42 a 1, la superficie, subir, 42.

14 42, ¡que te sostenga la cabeza!

15 13, de la decimotercera, a la\(30^{\prime}\) que se ha ido

16 subir,\(6^{\circ} 30^{\prime}\) a dos break:\(3^{\circ} 15^{\prime}\).

17\(3^{\circ} 15^{\prime}\) junto con\(3^{\circ} 15^{\prime}\) make hold:\(10^{\circ} 33^{\prime} 45^{\prime \prime}\).

18 To\(10^{\circ} 33^{\prime} 45^{\prime \prime}\), 42 que sostiene tu cabeza

19 unirse,\(52^{\circ} 33^{\prime} 45^{\prime \prime}\).

20 ¿El igual de\(52^{\circ} 33^{\prime} 45^{\prime \prime}\) qué? \(7^{\circ} 15^{\prime}\).

21\(7^{\circ} 15^{\prime}\) y\(7^{\circ} 15^{\prime}\), su contraparte, establece:

22\(3^{\circ} 15^{\prime}\), la bodega hecha, de una lágrima, a la otra se unen:

23 El primero es\(10^{\circ} 30\), el otro es 4.

24 Qué a 7, que sostiene tu cabeza, debo postular

25 lo que me\(10^{\circ} 30^{\prime}\) da? \(1^{\circ} 30^{\prime}\)postular. \(1^{\circ} 30^{\prime}\)a 7 elevar,

26\(10^{\circ} 30^{\prime}\) te da. \(1^{\circ} 30^{\prime}\)que has postergado es el igûm.

27 igi 6, que sostiene tu cabeza, despegar,\(10^{\prime}\).

28\(10^{\prime}\) a 4 subir,\(40^{\prime}\) es el igibûm.

29 Ya que\(1^{\circ} 30^{\prime}\) es el igûm,\(40^{\prime}\) es el igibûm, ¿la superficie es qué?

30\(1^{\circ} 30^{\prime}\), el igûm, a\(40^{\prime}\), el igibûm, subir, 1 es la superficie.

31\(1^{\circ} 30^{\prime}\), el igûm, y\(40^{\prime}\), el igibûm, montón:\(2^{\circ} 10^{\prime}\).

Rev.

1 ¿El decimotercer de\(2^{\circ} 10^{\prime}\) qué? \(10^{\prime}\).

2\(10^{\prime}\) a 6 repetir: 1, de\(1^{\circ} 30\),

3 el igûm, arranca:\(30^{\prime}\) te vas

Al igual que YBC 6967 (página 46), este problema trata de un par de números de la tabla de recprocals. Ambos textos hablan de su producto como “la superficie”, de acuerdo con la representación geométrica. Pero hay una diferencia: esta vez el producto es 1, no\(1`\) como en YBC 6967.

En cuanto a la estructura matemática y al procedimiento, se puede comparar con TMS IX #3 (página 57).

Str 368

Obv.

1 He tomado una caña, su medida no lo sé.

2 1 kùš he cortado. 1 sesenta (pasos a lo largo) la longitud he ido.

3 (Con) lo que he cortado lo he agrandado

4 con 30 (escalones) de ese (a lo largo) del ancho que he ido.

5\(6‵15\) es la superficie. La cabeza (longitud inicial) de la caña ¿qué?

6 Usted, por su procedimiento,

\(1‵\)Postura 7 y 30. (Para) la caña que no conoces

8 1 posit, a 1 sesenta que te has ido

9 levantas:\(1‵\) es la longitud falsa.

10 30 a esta 1 subida, 30 es la anchura falsa.

11 30, la anchura falsa a\(1‵\), la longitud falsa,

12 subir,\(30‵\) la superficie falsa.

13\(30‵\) a\(6‵15\), la verdadera superficie,

Rev.

1 aumento:\(3``` 7`` 30`\) te da.

2\(5′\) que has cortado a la falsa subida de longitud,

3 5 te da. 5 al falso aumento de ancho,

4\(2‵30\) te da. \(\frac{1}{2}\)de\(2‵30\) descanso,\(1‵15\)

5\(1‵15\) hacer encuentro,\(1`` 33` 45\)

6 para\(3``` 7`` 30`\) unirse,\(3``` 9`` 3` 45\).

7 ¿Qué es igual? \(13‵45\)es igual.

8\(1‵15\) que has hecho encuentro al interior se unen,

9\(15‵\) te da. igi\(30‵\), la superficie falsa, desprender,\(2^{\prime \prime}\).

10\(2^{\prime \prime}\) para\(15‵\) levantar,\(30′\) es la cabeza de la caña.

Esta es la versión rectangular de la “caña rota” (ver página 70), similar al IVA 7532. En esta variante, el campo es rectangular, y la caña se rompe una sola vez solamente.

YBC 6504 #1

Obv.

1 Tanto como el largo sobre el ancho va más allá, he hecho confrontarse, desde el interior de la superficie

2 Lo he arrancado:\(8^{\prime} 20^{\prime \prime}\). Largo sobre ancho\(10^{\prime}\) va más allá.

3 Por su procedimiento,\(10^{\prime}\) usted sostiene:

4\(1^{\prime} 40^{\prime \prime}\) a\(8^{\prime} 20^{\prime \prime}\) que te unes:\(10^{\prime}\) postula.

5 La mitad de\(10^{\prime}\) ustedes rompen:\(5^{\prime}\) postula.

6\(5^{\prime}\) haces bodega:\(25^{\prime \prime}\) postula.

7\(25^{\prime \prime}\), la superficie, a\(10^{\prime}\) que te unes:\(10^{\prime} 25^{\prime \prime}\) postulas.

8 Por\(10^{\prime} 25^{\prime \prime}\),\(25^{\prime}\) es igual. \(5^{\prime}\)para\(25^{\prime}\) unirte a:

9\(30^{\prime}\), la longitud, usted postula. \(5^{\prime}\)de\(25^{\prime}\) tu lágrima:

10\(20^{\prime}\), el ancho, postula.

Este problema trata del mismo rectángulo mutilado que #4 de la misma tablilla (ver página 79): Juntos, efectivamente, los cuatro problemas de la tablilla representan una variante en teresting del grupo cerrado donde se da la “superficie” de un rectángulo junto con la longitud; con la anchura; con la suma de los lados; o con su diferencia (ver nota 3, página 108). En la presente tablilla, la “superficie” es reemplazada en todas partes por el mismo rectángulo mutilado.

En este primer problema, conocemos el lado de la plaza que ha sido “arrancado”. Por lo tanto, se reduce fácilmente al tipo que conocemos por YBC 6967 (página 46). Al seguir las operaciones se debe tener en cuenta que el número\(10^{\prime}\) ocurre en dos roles diferentes.

Excepcionalmente en este tipo, la “unión” de\(5^{\prime}\) precede al “desgarro”. La tablilla parece pertenecer a la misma fase temprana y grupo de texto que AO 8862, y comparte esta particularidad con tres textos de Eshhunna (pertenecientes así a una fase incluso anterior). En efecto, parece que la escuela es responsable de la petición de que las operaciones siempre tengan sentido concreto, así como fue responsable de proscribir líneas generales —esta petición no es evidencia de “un intelecto primitivo que aún no está listo para la abstracción”, como se ha supuesto, sino de una mente crítica que refleja sobre cómo justificar lo que se hace.

YBC 6504 #3

Rev.

1 Tanto como el largo sobre el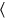 ancho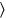 va más allá, hecho encuentro, desde el interior de la superficie he arrancado,

2\(8^{\prime} 20^{\prime \prime}\). \(30^{\prime}\)la longitud, su anchura ¿qué?

3 encuentro\(30^{\prime}\) hecho:\(15^{\prime}\) postula.

4\(8^{\prime} 20^{\prime \prime}\) de adentro\(15^{\prime}\) te arrancas,\(6^{\prime} 40^{\prime \prime}\) postulas.

5 La mitad de\(30^{\prime}\) ustedes rompen:

6 encuentro\(15^{\prime}\) hecho:\(3^{\prime} 45^{\prime \prime}\) postula.

7\(3^{\prime} 45^{\prime \prime}\) a\(6^{\prime} 40^{\prime \prime}\) que te unes:\(10^{\prime} 25^{\prime \prime}\) postula.

8 Por\(10^{\prime} 25^{\prime \prime}\),\(15^{\prime}\) es igual. \(15^{\prime}\)de\(25^{\prime}\) ti arranca:

9\(10^{\prime}\) postula. \(10^{\prime}\)de\(30^{\prime}\) ti arranca:

10\(20^{\prime}\), el ancho, postula.

\(\left(\ell-w, 30^{\prime}\right)\). Estos se pueden reconfigurar como un gnomon, como se muestra en el diagrama. Podemos ver el proceso como un “cambio de variable”, el problema ahora concierne a un cuadrado\(\square(\ell-w)\) y a 30 de sus lados, y su solución sigue el libro para tales problemas.

Figure47.png "/>

Figura\(2\): La geometría detrás de YBC 6504 #3, en proporciones ligeramente distorsionadas.

BM 85200+IVA 6599 #23

Rev. I

19 Una excavación. Tanto como he hecho confrontarse a sí mismo, y 1 kùš, yendo más allá, esa es la profundidad. \(1^{\circ} 45^{\prime}\)de suciedad que he arrancado.

20 Tú,\(5^{\prime}\), yendo más allá, a 1, la conversión,\(5^{\prime}\) subes, ves; a 12 subir, 1 ves.

21\(5^{\prime}\) hacer confrontarse a sí mismo,\(25^{\prime \prime}\) ya ves. \(25^{\prime \prime}\)a 1 subir,\(25^{\prime \prime}\) ya vees. igi 25 desprender,

22\(2‵24\) ya ves. \(2‵24\)para\(1^{\circ} 45^{\prime}\) levantar,\(4‵12\) ya ves.

23 de “igual, 1 unido”, 6 ^¿1^? es/son iguales (es). 6\(5^{\prime}\) subir,\(30^{\prime}\) ya ves, se enfrenta a sí mismo. 6 (error para 7) la profundidad.

24 El procedimiento.

Este problema proviene de la misma tablilla que el “problema de excavación” BM 85200+IVA 6599 #6 que se trató anteriormente (página 89), y su solución sigue los mismos principios. Ahora el “suelo” es cuadrado, y la profundidad excede el lado de 1 kùš. Como “cuerpo de referencia” se elige un cubo de lado 1 kùš, que permite el uso de una tabla de\(n^{2} \cdot(n+1)\), llamada “igual, 1 unido”. Se han encontrado tablas de este tipo.

Db ₂ —146

Obv.

1 Si, sobre un (rectángulo con) diagonal, (alguien) te pregunta

2 así,\(1^{\circ} 15\) la diagonal,\(45^{\prime}\) la superficie;

3 de largo y ancho correspondientes a qué? Usted, por su procedimiento,

4\(1^{\circ} 15^{\prime}\), su diagonal, su contraparte establece:

5 hacerlos sostener:\(1^{\circ} 33^{\prime} 45^{\prime \prime}\) sube,

6\(1^{\circ} 33^{\prime} 45^{\prime \prime}\) ^¿puede tu^? mano ^¿sostener^?

7\(45^{\prime}\) tu superficie a dos trae:\(1^{\circ} 30^{\prime}\) sube.

8 De\(1^{\circ} 33^{\prime} 45^{\prime \prime}\) corte: {...}\(3^{\prime} 45^{\prime \prime}\) el resto.

9 El igual de\(3^{\prime} 45^{\prime \prime}\) toma:\(15^{\prime}\) sube. Su media parte,

10\(7^{\prime} 30^{\prime \prime}\) sube, para\(7^{\prime} 30^{\prime \prime}\) levantar:\(56^{\prime \prime} 15^{\prime \prime \prime}\) sube

11\(56^{\prime \prime} 15^{\prime \prime \prime}\) tu mano. \(45^{\prime}\)tu superficie sobre tu mano,

\(45^{\prime} 56^{\prime \prime} 15^{\prime \prime \prime}\)Aparece 12. El igual de\(45^{\prime} 56^{\prime \prime} 15^{\prime \prime \prime}\) tomar:

13\(52^{\prime} 30^{\prime \prime}\) sube,\(52^{\prime} 30^{\prime \prime}\) su contraparte se acostó,

14\(7^{\prime} 30^{\prime \prime}\) que has hecho aferrarte a uno

15 unirse: de uno

16 cortado. 1 tu largo, 45 el ancho. Si 1 la longitud,

17 45 el ancho, la superficie y la diagonal correspondientes a qué?

18 Tú, por tu fabricación, la longitud te aferras:

19 1 sube... que tu cabeza sostenga.

Rev.

20...:\(45^{\prime}\), el ancho, hacer bodega:

\(33^{\prime} 45^{\prime \prime}\)Aparece el 21. A su longitud se unen:

22\(1^{\circ} 33^{\prime} 45^{\prime \prime}\) aparece. El igual de\(1^{\circ} 33^{\prime} 45^{\prime \prime}\) tomar:

23\(1^{\circ} 15^{\prime}\) surge. \(1^{\circ} 15^{\prime}\)tu diagonal. Su longitud

24 a la subida de ancho,\(45^{\prime}\) su superficie.

25 Así el procedimiento.

Este es uno de los textos de la región de Eshhunna, y así pertenece a la fase más temprana (y como vemos, utiliza la frase “a uno unirse, de un corte”, sin respetar la “norma de concreción”). Con justa precisión se puede fechar a c. 1775 a. C. El problema es uno de los acertijos que la Antigua escuela babilónica tomó prestados de los topógrafos acadios (ver páginas 106 107); resulta, resuelto precisamente de la misma manera, en un manual hebreo del 116 ce, es decir, 1900 años después. En el texto vemos varias reminiscencias de este origen, por ejemplo el pasaje introductorio “Si, sobre un (ractangle con) diagonal, (alguien) te pregunta así” y la referencia al cuadrado en la longitud en la línea 21 simplemente como “tu longitud”; ambas características reverberan en BM 13901 #23.

Figura\(3\): La geometría de Db _2-146.

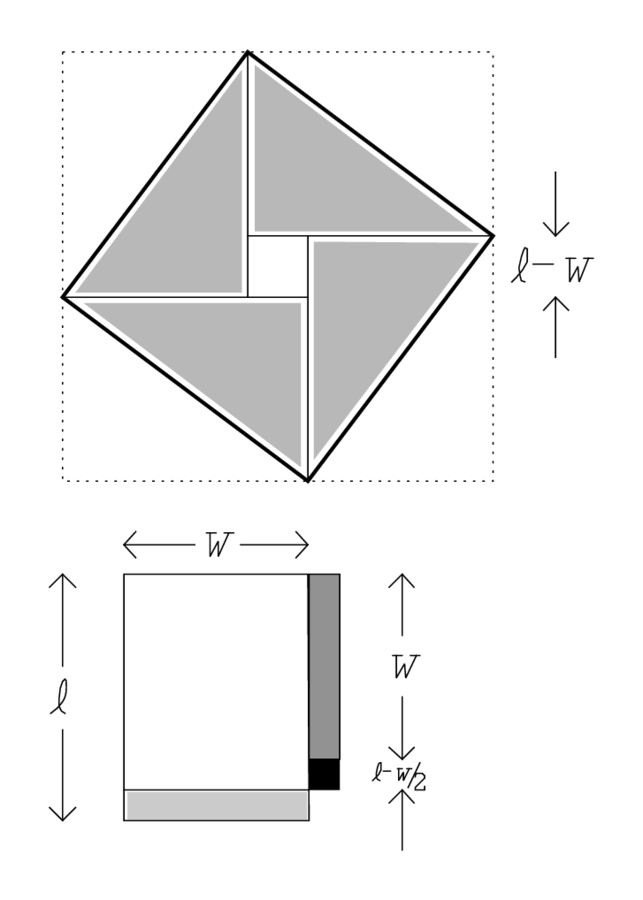
Las líneas 1-9 encuentran la diferencia entre la longitud y la anchura del rectángulo; el método se muestra en la parte superior de la Figura 3. Posteriormente, se encuentran los lados a partir de esta diferencia y el área por el procedimiento que ya conocemos perfectamente, por ejemplo de YBC 6967 (ver página 46), y que corresponde al diagrama inferior de la figura. (Sin embargo, el uso de “elevar” en la Obv. 10 muestra que el procedimiento se supone que está soportado por el diagrama superior ya existente).

La “mano” de las líneas 6 y 11 es una referencia al tablero de ajuste de cuentas en el que la calculadora realizó sus adiciones y restas. La “media parte” de la línea 9 (muttatum) es sinónimo de “resto”.

Al final tenemos pruebas con un rastro inconfundible de la “regla pitagórica” en formulación abstracta (la longitud se mantiene, sin la identificación habitual de su valor numérico).

Notas al pie

1

La tablilla está dañada en este punto, pero las huellas de signos que quedan bien podrían provenir de la palabra takkirtum, que significa “cambio” o “modificación” pero no ocurre en otros textos matemáticos. En todo caso, esta duda filológica no toca la interpretación del procedimiento matemático.