4.6: Evolución de la Virulencia

Última actualización
Guardar como PDF

Page ID: 117595

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Los microorganismos evolucionan continuamente debido a las presiones de selección en sus ambientes. Los antibióticos son una fuente común de presión de selección sobre las bacterias patógenas, y el desarrollo de cepas resistentes a los antibióticos presenta un importante desafío para la salud de la ciencia médica. Las bacterias y los virus también compiten directamente entre sí por el éxito reproductivo que resulta en la evolución de la virulencia. Aquí, utilizando el modelo de enfermedad endémica SIR, estudiamos cómo puede evolucionar la virulencia.

En aras de la argumentación, asumiremos que una población está inicialmente en equilibrio con una enfermedad endémica causada por un virus de tipo silvestre; es decir,$S, I$ y$R$ se supone que son distintos de cero y en valores de equilibrio. Ahora supongamos que algunas partículas de virus mutan por un proceso aleatorio, no dirigido que ocurre de forma natural. Queremos determinar las condiciones bajo las cuales el virus mutante reemplazará al virus de tipo silvestre en la población. En términos matemáticos, queremos determinar la estabilidad lineal del equilibrio de la enfermedad endémica a la introducción de una cepa viral mutante.

Suponemos que el virus de tipo silvestre original tiene tasa de infección$\beta$$\gamma$, tasa de eliminación y tasa de mortalidad relacionada con la enfermedad$c$, y que el virus mutante tiene tasas correspondientes$\beta^{\prime}, \gamma^{\prime}$ y$c^{\prime} .$ asumimos además que un el individuo infectado con un virus de tipo silvestre o mutante gana inmunidad a la infección posterior tanto de formas virales de tipo silvestre como mutantes. Por lo tanto, nuestro modelo tiene una sola clase susceptible$S$, dos clases infecciosas distintas$I$ y$I^{\prime}$ dependiendo del virus que cause la infección, y una sola clase recuperada$R$. El diagrama apropiado es

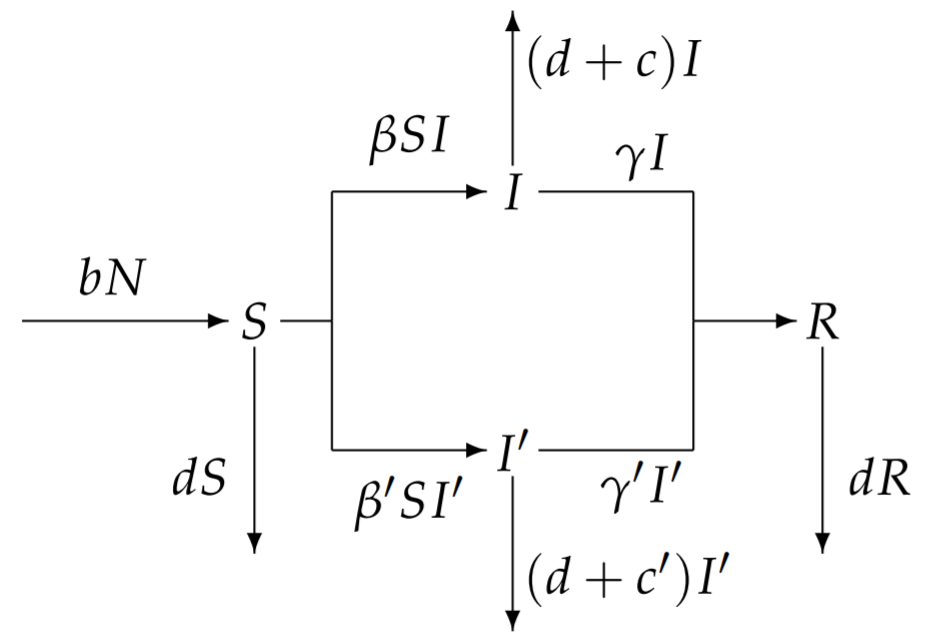
$clipboard_e1e1983ef71bdd1678a1c14b188424480.png$

con ecuaciones diferenciales correspondientes

\[\begin{align} \frac{d S}{d t} &=b N-d S-S\left(\beta I+\beta^{\prime} I^{\prime}\right) \\[4pt] \frac{d I}{d t} &=\beta S I-(d+c+\gamma) I \\[4pt] \frac{d I^{\prime}}{d t} &=\beta^{\prime} S I^{\prime}-\left(d+c^{\prime}+\gamma^{\prime}\right) I^{\prime} \\[4pt] \frac{d R}{d t} &=\gamma I+\gamma^{\prime} I^{\prime}-d R \end{align} \nonumber \]

Si la población está inicialmente en equilibrio con el virus de tipo silvestre, entonces tenemos$\dot{I}=0$ con$I \neq 0$, y el valor de equilibrio para$S$ se determina a partir de (4.6.2) para ser

\[S_{*}=\frac{d+c+\gamma}{\beta}, \nonumber \]

que corresponde a una relación reproductiva básica$\beta S_{*} /(d+c+\gamma)$ de unidad.

Perturbimos este equilibrio de enfermedad endémica introduciendo un pequeño número de infecciosos portadores del virus mutado, es decir, al dejar$I^{\prime}$ ser pequeños. En lugar de resolver el problema de estabilidad mediante un análisis jacobiano, podemos examinar directamente la ecuación para$d I^{\prime} / d t$ dada por (4.6.3). Aquí, con$S=S_{*}$ dado por (4.6.5), tenemos

\[\frac{d I^{\prime}}{d t}=\left[\frac{\beta^{\prime}(d+c+\gamma)}{\beta}-\left(d+c^{\prime}+\gamma^{\prime}\right)\right] I^{\prime} \nonumber \]

y$I^{\prime}$ aumenta exponencialmente si

\[\frac{\beta^{\prime}(d+c+\gamma)}{\beta}-\left(d+c^{\prime}+\gamma^{\prime}\right)>0 \nonumber \]

o después de algún álgebra elemental,

\[\frac{\beta^{\prime}}{d+c^{\prime}+\gamma^{\prime}}>\frac{\beta}{d+c+\gamma} \nonumber \]

Nuestro resultado (4.6.8) sugiere que los virus endémicos (u otros microorganismos) tenderán a evolucionar (i) para transmitirse más fácilmente entre las personas$\left(\beta^{\prime}>\beta\right) ;$ (ii) para hacer que las personas enfermen más tiempo$\left(\gamma^{\prime}<\gamma\right)$, y; (iii) ser menos mortales$c^{\prime}<c$. En otras palabras, los virus evolucionan para aumentar sus proporciones reproductivas básicas. Por ejemplo, nuestro modelo sugiere que los virus evolucionan para ser menos mortales porque los muertos no propagan la enfermedad. Nuestro resultado no sería aplicable, sin embargo, si los muertos de hecho propagaran la enfermedad, posibilidad si la disposición de los muertos no se hacía con el cuidado suficiente, tal vez por ciertas tradiciones culturales como el lavado familiar del cadáver.