3.3: Linealidad local

Última actualización
Guardar como PDF

Page ID: 116012

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Las dos últimas secciones examinaron la tasa de cambio tanto en el caso discreto como en el continuo. La primera aplicación de tasa de cambio en un punto es hacer proyecciones para valores de la función cercanos a ese punto. Queremos encontrar la ecuación de una función lineal que pueda ser utilizada para aproximar nuestra función. Esto es sencillo usando la versión punto-pendiente de una ecuación lineal.

Para el caso discreto, dada una función$y=f(x)\text{,}$ donde conocemos el valor de,$mf(a+1)\text{,}$ el cambio marginal en$f(x)$ para llegar a$x=a+1\text{,}$ entonces nuestra aproximación lineal discreta tiene la forma:

\[ \text{discrete linear}\, f_a (x)=f(a)+mf(a+1)*(x-a)\text{.} \nonumber \]

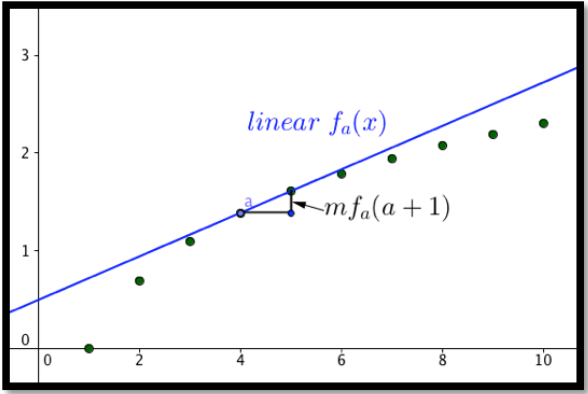
$clipboard_e338acbee7dbcd69c795579fd3aca9470.png$

En el caso diferenciable, dada una función$y=f(x)\text{,}$ donde conocemos el valor de,$f'(a)\text{,}$ la derivada de$f(x)$ al$x=a\text{,}$ entonces nuestra aproximación lineal tiene la forma:

\[ \linear f_a (x)=f(a)+f'(a)*(x-a)\text{.} \nonumber \]

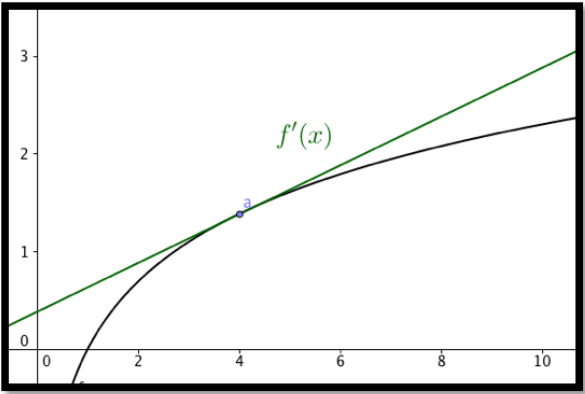
$clipboard_e16a113bf40165544829474f26d172a7a.png$

Las dos fórmulas son casi las mismas. El caso discreto utiliza la pendiente de una línea secante obtenida al observar puntos donde los valores x difieren en 1. En el caso diferenciable observamos la pendiente de la línea tangente. Una de las razones para observar la aproximación lineal de una función es que las funciones lineales son fáciles de evaluar.

Ejemplo 3.3.1: Estimación de Ganancias.

El beneficio de vender 10,000 gizmos es de 487,253 dólares. También sabemos que la ganancia marginal (10001) =$45. Estimar el beneficio de vender 10,013 gizmos.

Solución

Utilizamos la fórmula de arriba:

\[ \text{discrete linear profit}_a (x)=\profit(a)+\Mprofit(a+1)*(x-a)\text{.} \nonumber \]

Relleno de los valores del problema rinde:

\ begin {align*}\ text {beneficio lineal discreto} _ {10000} (x)\ amp =487253+45* (x-10000)\\ texto {beneficio lineal discreto} _ {10000} (10013)\ amp =487253+45* (13) =487838\ text {.} \ end {alinear*}

Por lo tanto, estimamos que la ganancia de la venta de 10013 gizmos es de 487,838 dólares.

Ejemplo 3.3.2: Estimación de Raíces Cuadradas.

Figura$3.3.3.$ Video presentación de este ejemplo

Usa la información acerca$f(x)=\sqrt{x}$ de cerca$x_0=100$ para estimar las raíces cuadradas del 96 al 104. Comprueba la exactitud de tus aproximaciones.

Solución

Primero usamos Excel para encontrar el valor de la función y su derivada en 100. Para la derivada utilizamos la aproximación de la calculadora.

$clipboard_e1ff2b00d602f9a5142e991a27e412e1f.png$

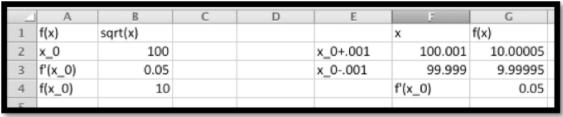
$clipboard_ece023e5a8c6042a28f7e11a86edf8d30.png$

Por lo tanto, la aproximación lineal es

\ begin {alinear*}\ lineal f (x)\ amp = f (100) +f' (100) (x-100)\\ amp =10+ (0.05) (x-100)\ text {.} \ end {alinear*}

Podemos configurar la hoja de trabajo para calcular la aproximación y darnos el error, tanto como número como como porcentaje de la respuesta correcta.

$clipboard_eab3dc50341d59a30db34ccbe758c20cd.png$

$clipboard_e8299ca72f91b90ab52df18df8261b53a.png$

Entonces es sencillo calcular valores y verificar la precisión. En el dominio dado, la aproximación lineal tiene un error por debajo de 0.03%.

Ejemplo 3.3.4: Estimación de Reciprocales.

Figura$3.3.5.$ Video presentación de este ejemplo

Utilice la información acerca$f(x)=100/x$ de near$x_0=400$ para estimar los recíprocos de los enteros de 396 a 404. Comprueba la exactitud de tus aproximaciones.

Solución

Una vez más, utilizamos Excel para encontrar el valor de la función y su derivada en 400. Para la derivada utilizamos la aproximación de la calculadora.

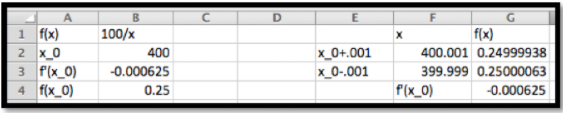
$clipboard_e44743c74ca75df0d5da6994854cc5068.png$

Por lo tanto, la aproximación lineal es

\ begin {alinear*}\ lineal f (x)\ amp = f (400) +f' (400) (x-400)\\ amp =.25+ (-0.000625) (x-400)\ text {.} \ end {alinear*}

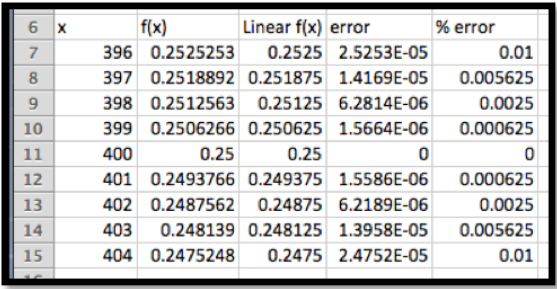
$clipboard_ee7e4ff6d4717b380c7a7b552810dc9bc.png$

Entonces es sencillo calcular valores y verificar la precisión. En el dominio dado, la aproximación lineal tiene un error por debajo de 0.01%.

Ejemplo 3.3.6: Estimación de funciones exponenciales.

Figura$3.3.7.$ Video presentación de este ejemplo

Para aproximar el interés con la composición continua es útil tener una aproximación lineal de$f(r)=exp(r)$ cuando$r$ está cerca de 0. Usa la información acerca$f(r)=exp(r)$ de near$r_0=0$ para estimar la función exponencial para números cercanos a 0. Comprueba la precisión de tus aproximaciones y da un dominio donde la aproximación sea lo suficientemente buena para usar.

Solución

Una vez más, utilizamos Excel para encontrar el valor de la función y su derivada en 0. Para la derivada utilizamos la aproximación de la calculadora.

$clipboard_e7fa60fd4397a5e6f47fd29feb3897c3f.png$

Por lo tanto, la aproximación lineal es

\ begin {alinear*}\ lineal f (x)\ amp = f (0) +f' (0) (r-0)\\ amp = 1+ (1) (r)\ text {.} \ end {alinear*}

Esto es mucho más fácil de calcular que la función exponencial. Sin embargo cuando comprobamos la precisión nos encontramos con que no es muy precisa para otros valores enteros.

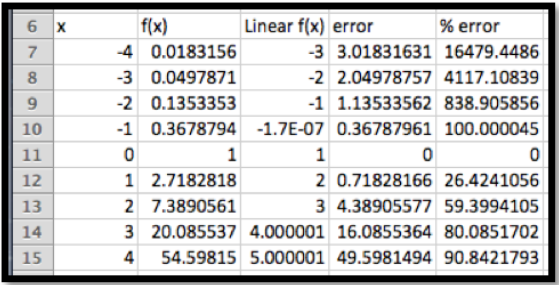
$clipboard_ee9cefc4ed3983ca13db3904c081f43b1.png$

Eso nos lleva de vuelta a la última parte de la pregunta, que pide un dominio donde la aproximación sea lo suficientemente buena para usar. La frase “lo suficientemente buena para usar” dependerá de la configuración, pero estaremos contentos con una estimación que esté dentro del 1%. Ya que vamos a utilizar esto para las tasas de interés, nos interesan las tasas positivas.

Modificamos la hoja de trabajo para permitir el uso de un tamaño de paso.$\Delta x\text{,}$ Luego experimentamos con el tamaño del paso hasta que obtenemos un dominio donde el error está por debajo del 1%.

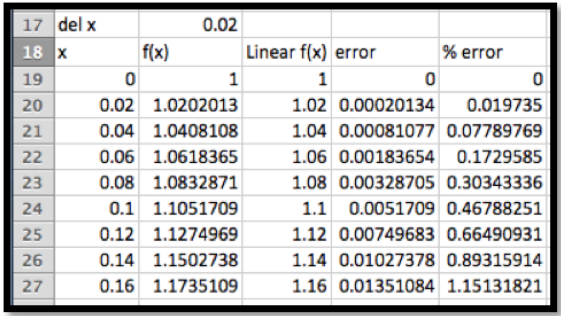
$clipboard_e4129ecac7cecd7db355e4c54348c5500.png$

Vemos que$\exp(r)\approx 1+r$ para$0\le r\lt 0.15\text{.}$ Esto nos da una aproximación que podemos utilizar para tarifas de hasta 15%.

El último ejemplo ilustra que las aproximaciones lineales solo deben usarse para un dominio limitado. El tamaño del dominio donde la aproximación lineal es “suficientemente buena” dependerá de la definición de “suficientemente bueno” o del error aceptable en nuestra aproximación. El buen dominio también dependerá de qué tan lejos esté la gráfica de lo lineal, o de qué tan rápido se esté doblando.

clase=”

Ejercicios: Linealidad Local

Para el ejercicio$3.3.1–3.3.5$, para la función dada y el valor para$x_0\text{:}$

Dar la fórmula para la aproximación lineal discreta.
Evaluar la aproximación en$x_1\text{.}$

Ejercicio 1:

$x_0=10\text{,}$$f(10)=50\text{,}$$mf(11)=6\text{,}$y$x_1=15\text{.}$

Contestar: \ begin {align*} f (x)\ amp\ approx f (10) +mf (11) * (x-10)\\ f (x)\ amp\ approx 50+6* (x-10)\ text {.} \ end {alinear*}

A continuación evaluamos la aproximación lineal a 15:

\[ f(15)\approx 50+6*(15-10)=50+30=80\text{.} \nonumber \]

Ejercicio 2:

$x_0=15\text{,}$$\profit(15)=50\text{,}$$\Mprofit(16)=2\text{,}$y$x_1=6\text{.}$

Ejercicio 3:

$x_0=20\text{,}$$f(19)=191\text{,}$$f(20)=200\text{,}$$f(21)=210\text{,}$y$x_1=28\text{.}$

Contestar: \[ f(x)\approx f(20)+mf(21)*(x-20)\text{.} \nonumber \]

Tenga en cuenta que tenemos que computar$mf(21)\text{.}$

\ begin {align*} mf (21)\ amp =f (21) -f (20) = 210-200=10\\ f (x)\ amp\ approx 200+10* (x-20)\ text {.} \ end {alinear*}

A continuación evaluamos la aproximación lineal a 28:

\[ f(28)\approx 200+10*(28-20)=200+80=280\text{.} \nonumber \]

Ejercicio 4:

$x_0=50\text{,}$$\revenue(49)=1007\text{,}$$\revenue(50)=1000\text{,}$$\revenue(51)=994\text{,}$y$x_1=45\text{.}$

Ejercicio 5:

$x_0=100\text{,}$$cost(99)=3740\text{,}$$cost(100)=3743\text{,}$$cost(101)=3754\text{,}$y$x_1=112\text{.}$

Contestar: \[ \cost(x)\approx \cost(100)+\Mcost(101)*(x-100)\text{.} \nonumber \]

Tenga en cuenta que tenemos que computar$\Mcost(101)$

\ begin {reunir*}\ Mcosto (101) =\ costo (101) -\ costo (100) =3754-3743=11\\ costo (x)\ approx3743+11* (x-100)\ text {.} \ end {reunir*}

A continuación evaluamos la aproximación lineal en 112:

\[ \cost(112)\approx 3743+11*(112-100)=3743+132=3875\text{.} \nonumber \]

Para el ejercicio$3.3.6–3.3.10$, para la función dada y el valor para$x_0\text{:}$

Calcular la aproximación numérica de la derivada en$x_0\text{.}$
Dar la fórmula para la aproximación lineal en ese punto.
Evaluar la aproximación en$x_1\text{.}$
Evaluar la función en$x_1$ y calcular la precisión de la aproximación.

Ejercicio 6:

$f(x)=\ln(x)\text{,}$$x_0=100\text{,}$y$x_1=105\text{.}$

Ejercicio 7:

$g(x)=\sqrt{x}\text{,}$$x_0=81$y$x_1=85\text{.}$

Contestar

\[ g(x)\approx g(81)+g'(81)*(x-81)\text{.} \nonumber \]

\[ g'(81)\approx \frac{g(81+.001)-g(81-.001)}{0.002}= \frac{\sqrt{81.001}-\sqrt{80.999}}{0.002}=.056\text{.} \nonumber \]