3.4: Optimización

Última actualización
Guardar como PDF

Page ID: 116011

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En la Sección 3.2 notamos que los puntos altos y bajos de la gráfica de una función a menudo coincidieron con un punto donde la derivada de la función era 0. En un entorno empresarial, a menudo nos preocupa encontrar los valores máximos y mínimos de una función, porque uno u otro será el mejor, u óptimo valor. Por lo general, queremos maximizar funciones como ganancias, servicios públicos, ingresos y participación de mercado. Por lo general, queremos minimizar funciones como el costo y la responsabilidad. Utilizaremos el mismo proceso básico para optimizar, si el extremo que estamos encontrando es máximo y mínimo.

Recordemos, dijimos que la derivada puede ser pensada como la pendiente de la línea aparente, obtenida al hacer zoom en la gráfica de una función. Claramente, no podemos tener un extremo en un punto interior del dominio si la derivada es distinta de cero, porque podríamos ir ya sea más alto o más bajo moviéndonos un poco hacia la derecha o hacia la izquierda. Así solo podemos tener extremos en un punto crítico, un lugar cuando la derivada es cero o indefinida, o en un punto final donde no podemos ir tanto a la izquierda como a la derecha. Esto nos da una pequeña lista de puntos candidatos para el valor óptimo.

Nuestro proceso de optimización será encontrar todos los puntos candidatos, luego ver cuál da los valores más altos y más bajos. Cuando nuestra curva tiene un punto que es máximo o mínimo en algún intervalo alrededor del punto, lo llamamos máximo o mínimo relativo. Si es el punto más alto o más bajo para todo el dominio de la función se denomina máximo o mínimo global.

Ejemplo 3.4.1: Función de Beneficio para Widgets.

Figura$3.4.2.$ Video presentación de este ejemplo

Hemos determinado que la función de ganancia para vender widgets es

\[ \profit(\quantity)=\quantity*(400-\quantity)-5000\text{,} \nonumber \]

con la función válida en el intervalo$0\le \quantity\le 500\text{.}$ Encuentra el beneficio mínimo y máximo en el intervalo dado.

Solución

Solución. 1 Solución A: sin cálculo

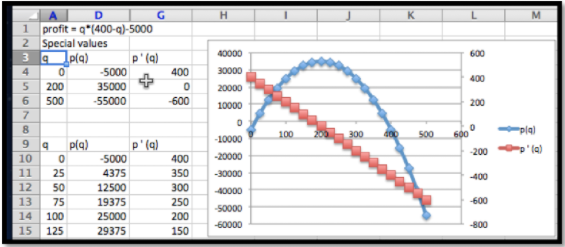
Se eligió el primer ejemplo porque se puede hacer sin usar ningún cálculo, por lo que primero lo resolvemos con métodos más fáciles. La función de ganancia es una función cuadrática en cantidad, por lo que es una parábola que apunta hacia abajo. La ubicación del vértice es en la$\quantity=200\text{,}$ que obtenemos de los coeficientes de los términos cuadrático y lineal. Por lo tanto, tenemos que verificar este punto y los dos puntos finales. Conectando valores, obtenemos$(0,-5000)\text{,}$$(200, 35000)$ y$(500, -55000)\text{.}$ El máximo ocurre cuando vendemos 200 widgets y nuestra ganancia es de $35,000, el mínimo ocurre cuando vendemos 500 widgets y nuestra pérdida es de $55,000. Un mínimo relativo ocurre cuando vendemos 0 widgets y nuestra pérdida es de $5,000.

Solución. 2 Solución B: con cálculo

Queremos configurar el problema para poder graficar la función de ganancia y su derivada en la misma gráfica. Nos haremos la aproximación calculadora de la derivada. Como hicimos en la última sección, configuramos una hoja de trabajo con columnas para$q\text{,}$$q+.001\text{,}$$q-0.001\text{,}$$p(q)\text{,}$$p(q+.001)\text{,}$$p(q-0.001)\text{,}$ y$p'(q)\text{.}$ Esto permite que la mayor parte de la hoja de trabajo se complete con relleno rápido.

$clipboard_ecfe07b5ec062590b6b8b7107f349f823.png$

Luego miramos los valores, y comparamos la tabla con una gráfica. Encontramos los mismos tres puntos candidatos y los mismos valores máximos y mínimos.

$clipboard_e668d6351d4a9c81187ff5ad2978e3166.png$

Para un segundo ejemplo queremos mirar una función donde no podemos encontrar el máximo por medios algebraicos.

Ejemplo 3.4.3: Aceite de Cumquat.

Figura$3.4.4.$ Video presentación de este ejemplo

Hemos determinado que la función de ganancia para la venta de petróleo cumquat es

\[ \profit(\quantity)=(10\quantity-20)*exp(-\quantity/50)-10\text{.} \nonumber \]

Entendemos que la función es válida en el intervalo$0\le \quantity\le 400\text{,}$ donde la cantidad se mide en miles de pintas y el beneficio se mide en miles de dólares. Encuentra el beneficio mínimo y máximo en el intervalo dado.

Solución

La hoja de cálculo se configura como en el primer ejemplo, pero con la función cambiada.

$clipboard_efff061e016905d1cb49a0a92302d4f91.png$

Mirando la gráfica y la gráfica esperamos encontrar mínimos locales en los puntos finales, y el máximo cuando$q$ está cerca de 50. Utilizamos meta buscar encontrar donde la derivada es cero. Como vemos a continuación, Goal Seek no encuentra un punto donde la derivada sea cero. En cambio, encuentra un punto donde la derivada está “lo suficientemente cerca” a cero. Por defecto, Excel entiende que “lo suficientemente cerca” está dentro de 0.001.

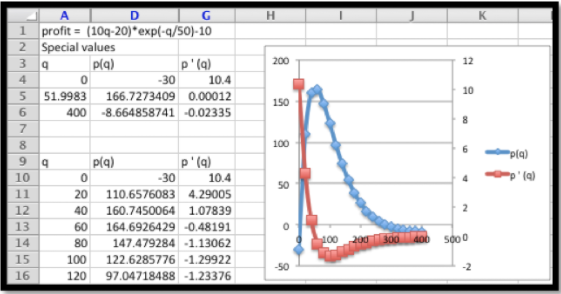
$clipboard_e84ea9bcad84be21d9b9fa105540e1ce2.png$

Si la definición por defecto de “lo suficientemente cerca” es lo suficientemente buena para nuestros fines, entonces la ganancia máxima de $166,727 ocurre cuando vendemos 51,998 pintas de petróleo. (De hecho, vender 2 pintas más de petróleo arrojará 0.01 centavos adicionales.) El beneficio mínimo ocurre cuando no vendemos ningún producto, en cuyo caso tenemos una pérdida de $30,000.

Una de las cosas a tener en cuenta sobre el último ejemplo es la robustez del método. Desde un punto de vista algebraico, la función era bastante fea. Todo lo que necesitábamos saber para usar el método era que la función era lo suficientemente suave, que cuando acercamos el zoom a una escala de$x$ cambio de 0.001 la gráfica parecía una línea recta.

A lo largo de la sección hemos buscado lugares donde la derivada sea cero cuando se busca extrema. No hemos prestado atención a cómo decidimos si el punto que encontramos es un máximo local o un mínimo local. Hay varios enfoques que podríamos usar. Ya que estamos calculando la derivada podríamos señalar que un máximo local es un lugar donde la función va de aumentar a disminuir, por lo que la derivada va de positiva a negativa. (De igual manera, un mínimo local se encuentra en un lugar donde la derivada va de positiva a negativa.) También hay una prueba que analiza la derivada de la derivada. Esas pruebas serán más útiles en el próximo capítulo cuando estemos encontrando una fórmula para la derivada por medios simbólicos. Sin embargo, con la técnica numérica que estamos utilizando, la prueba más fácil es que un máximo local sea mayor o igual a puntos un poco tanto a la izquierda como a la derecha. Simplemente conectamos puntos un poco a cada lado para probar. Dado que un cambio$q$ de 0.001 hace que la gráfica se vea como una línea recta plana, cambiamos$q$ por 0.01.

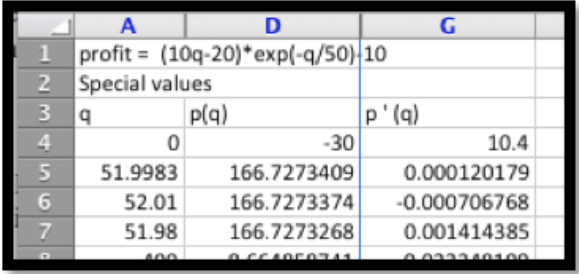
$clipboard_e9c98722e9a250c157bad58c48763776d.png$

Como se esperaba, las ganancias bajan a medida que nos alejamos de nuestro máximo esperado.

Ejemplo 3.4.5: Gizmo Profit.

Figura$3.4.6.$ Video presentación de este ejemplo

Una planta puede producir entre 150 y 300 artilugios. La función de ganancia para la planta es:

\[ \profit(\quantity)=4 \quantity^2-1300 \quantity+125000\text{.} \nonumber \]

Encuentra el nivel de producción que maximiza las ganancias.

Solución

Establecimos el problema como antes, utilizando la búsqueda de objetivos en la derivada para encontrar puntos críticos, y verificando los extremos del intervalo.

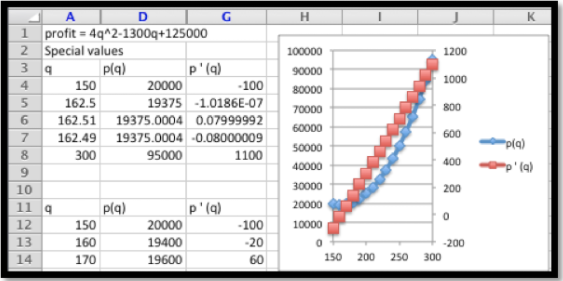
$clipboard_e805b176b90ee8b1280f5243112d8158e.png$

Tenemos tres candidatos para los extremos, los dos puntos finales y el punto crítico en 162.5. No obstante al mirar los puntos al lado del punto crítico, vemos que es un mínimo local. También vemos, el de nuestros 3 puntos candidatos, el que da el máximo beneficio es el punto final correcto, cuando la cantidad es de 300.

Para nuestros tres primeros ejemplos hemos estado tratando de encontrar el mínimo o máximo de una función que se nos ha dado en función de una variable. A veces necesitamos hacer un poco de trabajo para obtener la función en ese formato.

Ejemplo 3.4.7: Minimización de Costos de Materiales.

Figura$3.4.8.$ Video presentación de este ejemplo

Estoy fabricando goop, un líquido que hay que poner en latas. Usaremos latas que tengan una forma cilíndrica estándar. Encuentra la altura y el radio de una lata de 1 litro que utiliza una cantidad mínima de superficie metálica.

$clipboard_e568fc5219e6286530756495e7877b66d.png$

Solución

Usando geometría básica recordamos las fórmulas para el volumen y área de superficie de un cilindro.

\ begin {alinear*}\ texto {volumen}\ amp =\ pi\ texto {radio} ^2*\ texto {altura}\\ texto {área}\ amp =2\ pi\ texto {radio} ^2+2\ pi*\ texto {radio} *\ texto {altura} *\ texto {altura}\ texto {.} \ end {align*}

Ya que estoy midiendo volumen en litros, quiero medir radio y altura en decímetros para que las unidades funcionen correctamente. Para optimizar, necesitamos reducir el problema a una sola función de una sola variable. Se nos dice que el volumen es 1, por lo que podemos resolver para la altura en función del radio, luego enchufarlo a la ecuación para área. Entonces el área es una función de una sola variable, radio, y podemos encontrar los puntos críticos y verificar por un mínimo.

\ begin {alinear*}\ texto {altura}\ amp =1/ (\ pi\ texto {radio} ^2)\\\ texto {área}\ amp =2\ pi\ texto {radio} ^2+\ frac {2} {\ texto {radio}}\ texto {.} \ end {align*}

Como ahora tenemos área en función del radio variable único podemos tomar una derivada para encontrar el punto crítico, luego encontrar la forma óptima.

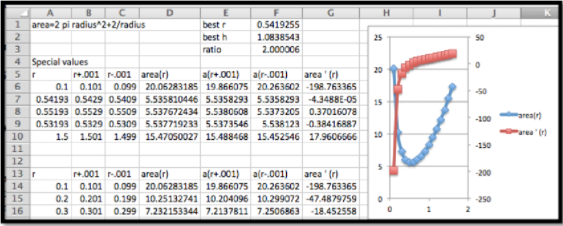
$clipboard_ef58b735ee3f27bc6aca6d96dfb34883e.png$

Resolviendo para donde la derivada de área es cero, encontramos que el radio de la lata debe ser de 0.5419 decilitros. Tapamos ese valor de nuevo en la fórmula para la altura en términos de radio y vemos que la altura debe ser de 1.083854 decilitros. Para entender la forma de la lata vemos que la altura es el doble del radio, o lo mismo que el diámetro de la lata. La lata tiene una forma óptima cuando es la forma de una lata de pintura grande.

Hay tres detalles técnicos dignos de mencionar del último ejemplo. Primero, en Excel, la mejor manera de poner$\pi$ una fórmula es con la constante PI (). Segundo, la función para área se define en un intervalo abierto donde el radio es positivo. No hay área máxima para una lata de volumen fijo. (Por ineficiente que sea nuestra lata, siempre podemos empeorarla, moviéndonos más lejos de lo óptimo). Tercero, también hay que señalar que para este problema, queríamos varios números como parte de nuestra respuesta. La hoja de trabajo para el problema pone la mejor altura y radio en la parte superior, donde el lector puede encontrarlo fácilmente.

En este último ejemplo tuvimos que reducir dos ecuaciones en dos incógnitas a una sola ecuación en una desconocida para poder optimizar. También es posible que necesitemos producir una ecuación a partir de datos.

Ejemplo 3.4.9: Ganancias maximizadas y puntos de equilibrio.

Figura$3.4.10.$ Video presentación de este ejemplo

Para la producción y venta de widgets tenemos los siguientes datos sobre ganancias basadas en ventas.

Cantidad	10	100	200	250	300	400
Beneficio	-$2,083	$31,040	48,587	49,845	46,146$	23,670

Encuentra los puntos de equilibrio y la cantidad que maximiza el beneficio.

Solución

Al mirar una gráfica rápida de los datos, voy a suponer que la función de ganancia es una parábola orientada hacia abajo, por lo que encuentro el polinomio cuadrático que mejor se ajuste a los datos. Usando líneas de tendencia, mi función de ganancia es

\[ \profit(q)=-1.002 q^2+477.22 q=6720.9\text{.} \nonumber \]

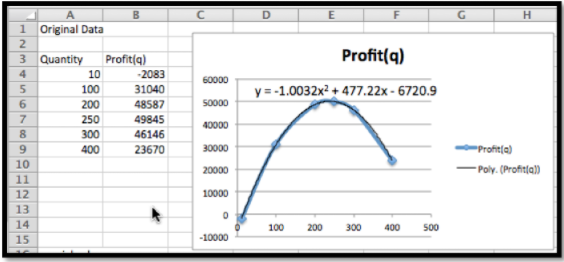
$clipboard_e6e28067d8ffff0d175ac9aced45e0f5b.png$

Ahora pongo la tabla para valores especiales con búsqueda de gol. Utilizo puntos de partida de 20 y 450 para los puntos de break even y 250 para el máximo. Para encontrar puntos de equilibrio, I Goal Seek sobre la función de ganancia. Para encontrar el punto máximo, I Goal Seek sobre la derivada de la función de ganancia.

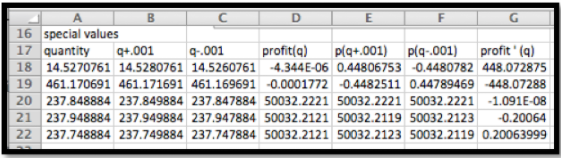
$clipboard_e10f085546c3e03f2583b767220c16c07.png$

Redondeando al número entero más cercano en cada caso, mis puntos de equilibrio son para vender 15 y 460 widgets. Mi ganancia máxima de $50,032 ocurre cuando vendo 238 widgets.

Ejemplo 3.4.11: Minimización de Gastos.

Figura$3.4.12.$ Video presentación de este ejemplo

Estamos dirigiendo un negocio y queremos minimizar los gastos de equipo. Para un equipo en particular, los costos pueden dividirse en gastos iniciales para comprar el equipo, gastos anuales fijos para mantener el equipo en el inventario y costos de reparación que anticipamos que aumentarán a medida que el equipo envejece. Una prensa de widgets cuesta $10,000 para comprar, y los gastos operativos son $500 al año, y los costos totales de reparación son$300t^2$ durante los primeros$t$ años. ¿Cuál es el tiempo óptimo para usar una prensa de widget antes de reemplazarla?

Solución

Mi ecuación de costo anual es el costo total dividido por$t\text{.}$ Este costo anual es:

\[ \AnnualCost(t)=10000/t+500+300t\text{.} \nonumber \]

Yo creo una hoja de cálculo que calcula el costo y su derivado durante los primeros 10 años.

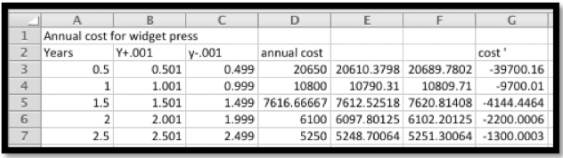
$clipboard_e9758fdd2c313d9021b030c540c3e4213.png$

Al observar los datos, el costo mínimo anual se obtiene manteniendo la prensa entre 5.5 y 6.0 años. Usando Goal seek en el derivado, encuentro que el costo mínimo anual de $3,964.10 se obtiene manteniendo la prensa por 5.77 años.

clase=”

Ejercicios: Optimización

Para la función y dominio dados:

Trazar la función y su derivada en la misma gráfica.
Identificar las regiones donde la función está aumentando y las regiones donde la función está disminuyendo.
Identificar el máximo y mínimo local para el dominio dado.
Identificar el máximo y mínimo global para el dominio dado

Ejercicio 1:

$f(x)=-2x^2+17x+23$en el intervalo$0\le x\le 50\text{.}$

Responder

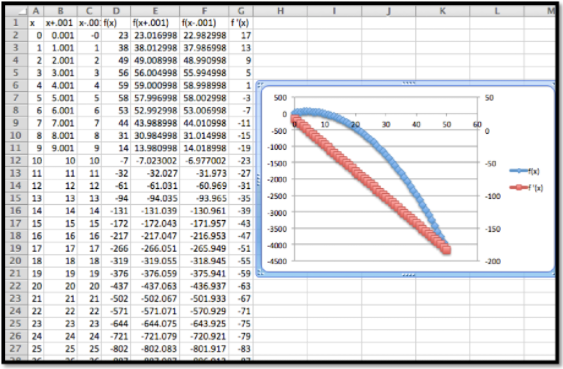
La configuración de estos problemas en Excel sigue el mismo proceso.

Creamos columnas para$x, x+.001, x-.001, f(x), f(x+.001), f(x-.001)\text{,}$ y$f'(x)$
Una vez que ingresas$f(x)\text{,}$ haciendo un relleno rápido correcto, encuentra fácilmente$f(x+.001)$$f(x-.001)\text{,}$ y luego$f'(x)$ es fácil de calcular.
Una vez que$f'\text{,}$ graficas$f$ y suele ser una buena idea graficar la derivada usando el eje secundario: haz doble clic en la función derivada y elige el botón apropiado en el cuadro de diálogo.

$clipboard_ea7a57c1bbc05628429bd6146271b4073.png$

La tabla se trunca en$x = 25\text{,}$ pero el resto se utilizó para crear la gráfica.