3.5: Una introducción a Solver

Última actualización
Guardar como PDF

Page ID: 116007

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Debemos esperar, siempre que veamos una operación que se usa mucho en el mundo de los negocios, que Excel tenga un comando bastante simple para lograr el resultado. En la sección 1.5 presentamos Goal Seek, una herramienta que forma parte de Excel, y que puede ser utilizada para resolver una ecuación para una raíz desde un punto de partida determinado. En la última sección, señalamos que se pueden encontrar candidatos para un máximo o mínimo local de una función al encontrar la derivada y usar Objetivo Buscar para encontrar donde la derivada es 0. En esta sección presentamos Solver, un Add-In to Excel. Es más fácil pensar en solver como una versión más poderosa de Goal Seek. Será más fácil caminar por el uso de Solver mientras se trabaja un ejemplo.

Ejemplo 3.5.1: Usar Solver para recopilar información sobre la Gráfica.

Figura Presentación en$3.5.2.$ video de este ejemplo

Dejar$f(x)=9 x-x^2+7$ en el intervalo$-1\le x \le 14\text{.}$

Solución

Como siempre, comenzamos por usar herramientas más simples. En este caso es útil tener Excel bosquejar una gráfica y utilizar la información que recabamos en curso previo. Por la forma de la función sabemos que la gráfica es una parábola que apunta hacia abajo.

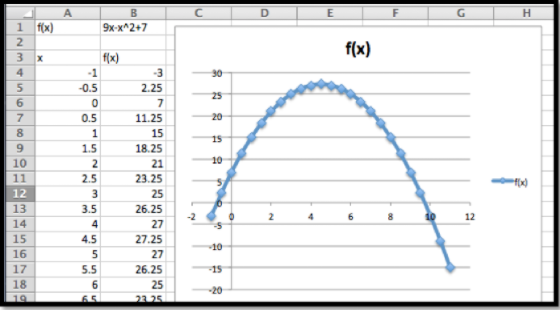
$clipboard_e6d04c1db7d91ddc14146589a879f1b27.png$

Mirando el gráfico y la imagen vemos que el vértice está cerca de También$x=4.5\text{.}$ vemos que las intercepciones x están cerca de$x=-0.5$ y$x=9.5\text{.}$

A continuación, queremos asegurarnos de que Solver esté instalado. Debe estar en la sección Análisis de la pestaña Datos.

$clipboard_e6c78f8a89efe27013f1d681517a77bc8.png$

Si no lo encuentra ahí, debe ir a la ayuda en línea para Excel, y buscar ayuda en Solver. Bajo el tema “Definir y resolver un problema usando Solver”, seleccione primero “Definir y resolver un problema”, luego “Si no ve Solver en Análisis en la pestaña Datos”.

Primero queremos usar Solver para encontrar una raíz. Usando el mismo enfoque que usamos con Goal seek, nos gustaría que la celda B5 se estableciera igual a 0 cambiando el valor de la celda A5. (Como hemos configurado el problema, podríamos usar solver comenzando con cualquiera de las celdas que dan un valor para que$f(x)\text{.}$ elegí la que tiene$f(x)$ más cerca del resultado deseado.)

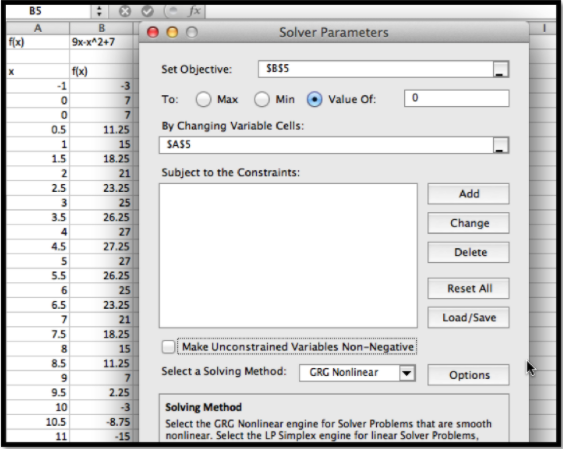
$clipboard_ee035f84b999f39c7f5540a214141bf93.png$

Solver encuentra una solución con Se$x=-0.72015\text{.}$ nos da un cuadro de diálogo que nos pregunta si queremos mantener la solución solucionador o restaurar nuestro valor original.

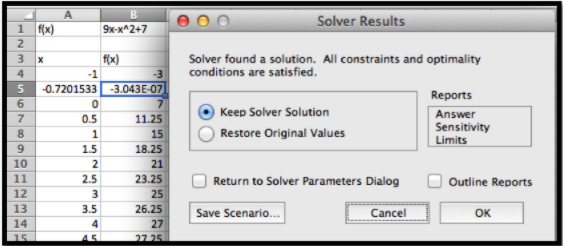
$clipboard_e901b9a38bfc97ce4e7262459b00b7a1a.png$

Al igual que con Goal Seek, si volvemos a usar Solver, comenzando por$x$ más cerca de 9, encontraremos una solución$x=9.72015\text{.}$

No obstante, la razón por la que presentamos Solver, es que puede hacer las cosas sería más difícil con Goal Seek. De la gráfica, y nuestro conocimiento o parábolas, sabemos que la gráfica tiene un solo máximo. Para encontrar el máximo con Goal Seek, necesitamos darnos cuenta de que el máximo ocurre cuando la derivada es 0, definir la derivada numérica, luego establecer la derivada igual a 0. Con Solver, simplemente le pedimos que encuentre el máximo. Encuentra el vértice en$x=4.5\text{.}$

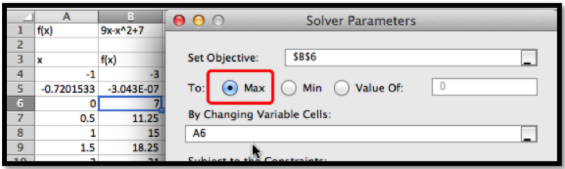
$clipboard_e3ba0ae909ed8261c4173c545f39cec4b.png$

También nos gustaría poder encontrar un mínimo. A partir de la imagen, sabemos que una parábola que apunta hacia abajo no tiene un mínimo absoluto. Sin embargo, en los negocios, normalmente nos preocupan las funciones definidas en un dominio finito. Para este problema, consideremos solo el intervalo$0\le x\le 15\text{.}$ Queremos que el mínimo aparezca en la celda B7, por lo que queremos constreñir la celda A7. Si iniciamos Solver, luego pulsamos el botón de agregar, obtenemos un cuadro de diálogo para ingresar la primera restricción, que A7$\ge 0\text{.}$

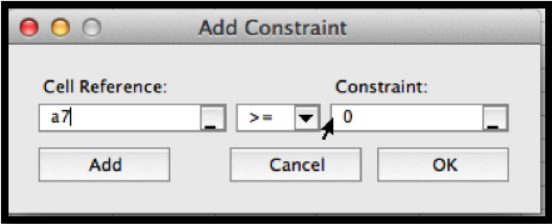
$clipboard_eeafcee625f76215c0cf197f453a5e1dc.png$

De manera similar, agregamos la restricción que A7 15 y le pedimos al solucionador un mínimo.

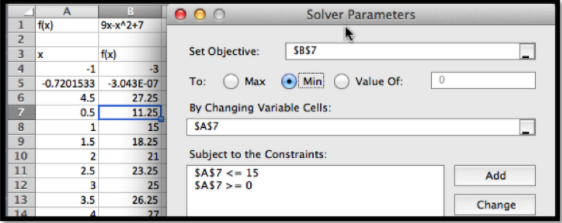
$clipboard_e83e3ed3670aa6a97d128a8c538122c4a.png$

Desde que iniciamos la búsqueda del mínimo en$x=0.5\text{,}$ Solver encuentra el mínimo en$x=0\text{.}$ Este es un “mínimo local”. Cualquier$x$ valor en el intervalo que está cerca da un valor mayor para la función.

También nos gustaría encontrar el mínimo al otro extremo del intervalo. Para ello es útil conocer un poco de las matemáticas detrás de lo que está haciendo solver. Solver utiliza derivados desde el punto de partida para decidir la dirección que debe mirar y hasta dónde debe llegar para encontrar la siguiente conjetura para su respuesta. Esta es una modificación de una técnica llamada método de Newton. En cuanto a nuestra imagen, dependiendo de si le decimos que encuentre un valor máximo, mínimo o especificado, Solver intenta deslizarse hacia arriba o hacia abajo de la gráfica hasta encontrar un buen candidato, lo que nos da como solución. En realidad está buscando el primer máximo o mínimo local al que llegue. No busca otros candidatos. Entonces si empezamos en$x=0.5$ él se deslizará hacia la izquierda para encontrar una respuesta. Para encontrar el mínimo en el otro extremo del intervalo necesitamos un punto de partida donde la gráfica ya esté inclinada hacia abajo hacia la derecha. Empezar en$x=8$ debería funcionar. Establecimos solucionador.

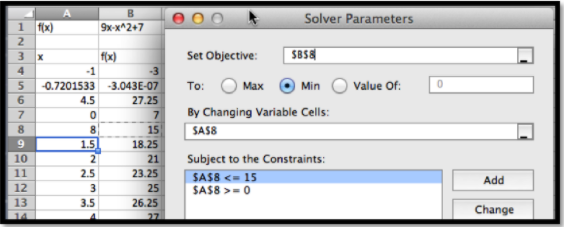
$clipboard_e5034f2b01a571a193e90549bbf4975a1.png$

Solver encuentra que la curva tuvo un mínimo en$x=15$ con$f(x)=-83\text{.}$

Para recapitular, usando Solver en el intervalo$0\le x\le 15\text{,}$ que encontramos tiene$x=9.72015\text{,}$ una raíz en un máximo en$x=4.5\text{,}$ y mínimos locales en$x=0$ y También$x=15\text{.}$ encontramos los valores de$f(x)$ en todos esos puntos. Sin embargo, se eligió este ejemplo porque podíamos obtener los mismos resultados con el trabajo simplemente usando las propiedades de las parábolas. Así, ahora queremos hacer las mismas preguntas sobre un problema que no podemos resolver algebraicamente.

Ejemplo 3.5.3: Una Gráfica Engañosa.

Figura Presentación en$3.5.4.$ video de este ejemplo

Use solver para recopilar información, sobre el intervalo$0\le x\le 15\text{,}$ en la gráfica de$f(x)=(x^3-4x^2+4x+3) e^{(-x/2)}\text{.}$

Solución

Como siempre, empieza por mirar una gráfica.

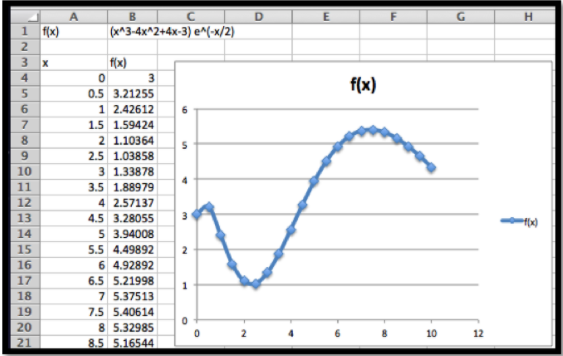
$clipboard_e6e8e9ee09accadd37c09b51cb17357aa.png$

De la gráfica espero que la función no tenga raíces en el intervalo. Tiene mínimos locales cerca de 0, 2.5 y 10. Tiene máximos locales cerca de 0.5, y 8. Voy a necesitar agregar restricciones para encontrar los mínimos locales en los límites. Para que mi hoja de trabajo sea fácil de leer agrego dos columnas adicionales para los valores x e y de punto interesante, y relleno conjeturas.

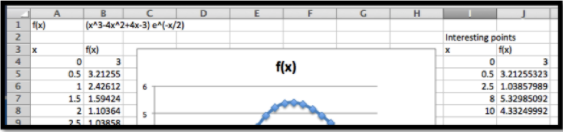
$clipboard_e5ac9a70f61a20b2b5c47959de130e72f.png$

Después de usar Solver, encuentro que los mínimos locales ocurren en 0, 2.326 y 10, y los máximos locales ocurren en 0.29115 y 7.3827. El valor máximo para la función en el intervalo es 5.409 y el mínimo es 1.0149. Verificamos que los puntos finales,$x=0$ y$x=10\text{,}$ son ambos mínimos locales.

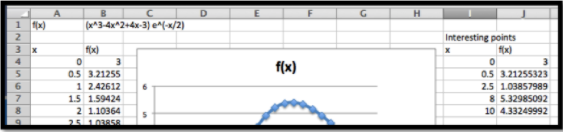
$clipboard_e1502c9d64a8ef5fc6b877f4d8e0d79c4.png$

Esta función puede ser utilizada para ilustrar una limitación de nuestro método. Si hubiéramos graficado las funciones a intervalos a intervalos de tamaño 1 en lugar de 0.5, obtenemos una imagen diferente.

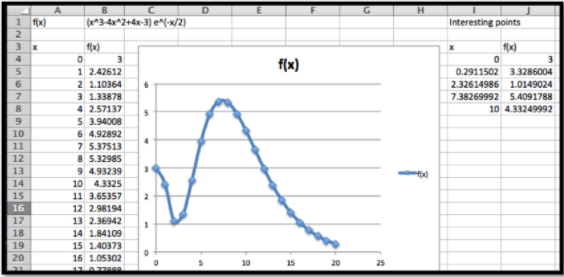
$clipboard_ef437f3df15ddcfc30e0c8927b0c8c9a4.png$

En ese caso, faltamos el máximo local en 0.29 y confundimos el punto final izquierdo con un máximo local. Dado que Solver no usa la imagen, no será engañada por ella. Este ejemplo señala que si bien la gráfica es útil como guía, necesitamos verificar que no hemos sido engañados al no graficar con suficiente resolución.

Advertencia: En Ejemplo$3.5.3$ vimos que confiar en la gráfica podría engañarnos. El otro lado es un ejemplo donde confiar en Solver puede engañarnos. Mencionamos anteriormente que Solver utiliza una variante del método de Newton para encontrar valores. En términos aproximados, encuentra repetidamente la aproximación lineal y se desliza hacia arriba o hacia abajo de esa línea hasta la respuesta deseada. Si empezamos cerca de la respuesta, este es un método muy efectivo para encontrar una solución numérica. Sin embargo es fácil construir problemas donde esto lleva a un callejón sin salida o a la respuesta equivocada. En particular, el método tiene gran dificultad con problemas donde la función no es diferenciable o donde tiene varias curvas. Considera el siguiente ejemplo.

Ejemplo 3.5.5: Solucionador Engañador.

Figura Presentación en$3.5.6.$ video de este ejemplo

Use solver para recopilar información, sobre el intervalo$-2\le x\le 2\text{,}$ en la gráfica de

\[ f(x)=\begin{cases} -5x-3\amp x\lt 0\\ 4(x-1)^2 \amp x \gt 0\\ \end{cases}\text{.} \nonumber \]

Solución

Como siempre, empieza por mirar una gráfica. Utilizamos la función IF para producir casos.

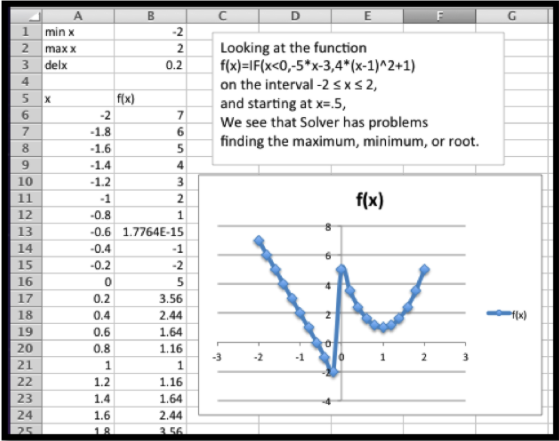
$clipboard_e8ad93c14939e2bbaeb177c3fe5214e32.png$

Es bastante fácil ver que la función alcanza un máximo de 7 at$x=-2\text{,}$ y tiene una raíz$x=-0.6\text{.}$ en En este intervalo la función no tiene un mínimo, pero se acerca a -3 cuando se$x$ acerca a 0 desde el lado negativo. Si empezamos en$x=0.5$ e intentamos deslizarnos hacia arriba o hacia abajo de la curva, vamos en la dirección equivocada para encontrar la raíz o el mínimo. Para encontrar el máximo también necesitamos bajar antes de poder subir al máximo.

Cuando miramos al solucionador, obtenemos los resultados equivocados pero esperados. La función no sólo deja de ser diferenciable en$x=0\text{,}$ ella tiene un salto ahí. Solver encuentra el máximo y mínimo local más cercano. Para la raíz, nos dice que no puede encontrar una solución factible.

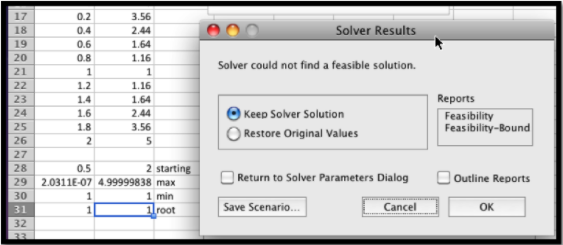
$clipboard_e945e82e70b8ca637cb2edd4667b615f8.png$

La lección que hay que aprender es que solucionador nos ayudará a encontrar nuestros puntos candidatos, pero aún así necesitamos entender el comportamiento de las funciones lo suficientemente bien como para dar un buen punto de partida.

Un avance de las cosas por venir — Extrema de funciones de dos variables.

Hay otra característica de Solver a la que volveremos más adelante en el curso. Goal Seek preguntó qué celda debería cambiarse para alcanzar nuestra meta deseada. Solver nos permite especificar un número de celdas que podemos cambiar. Esto significa que trabajará con funciones de varias variables. Esto nos permitirá arrojar algo de luz sobre una de las “cajas negras” que usamos anteriormente en este curso, la capacidad de Excel para encontrar una línea de tendencia, o la curva que mejor se ajuste a un conjunto de datos.

Ejemplo 3.5.7: Utilice Solver para encontrar una línea de mejor ajuste a un conjunto de datos.

Figura Presentación en$3.5.8.$ video de este ejemplo

Encuentre una línea de mejor ajuste a los siguientes datos.

x	1	2	3	4	5
y	35	46	78	84	114

Solución

Como mencionamos en la Sección 1.4, cuando se nos pide encontrar una línea de mejor ajuste, se nos pide crear una función de predicción$\prediction(x)=A x+B\text{,}$ con$A$ y se$B$ elige para minimizar la suma de los cuadrados del error entre los valores reales y los valores predichos. Construimos una hoja de trabajo que encuentra la suma de errores cuadrados. Comenzamos con nuestras variables, A y B, establecidas en 5.

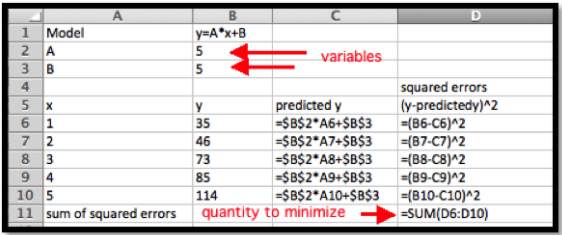
$clipboard_e3aac3fb9cc6b42307f354b3009e5359c.png$

Pedimos a Solver minimizar D11 cambiando B2 y B3. Para comparación pedimos el mejor ajuste Trendline usando la gráfica de dispersión.

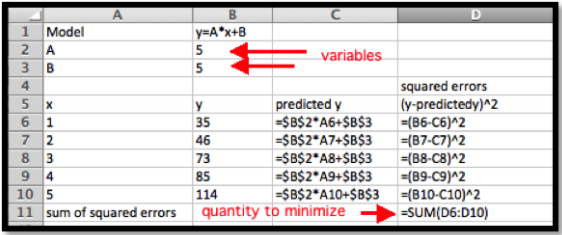
$clipboard_e30b641b6ce2757deb8c034c21621ade6.png$

Vemos que obtenemos las mismas respuestas, sujetas a reglas de redondeo.

La herramienta Trendline tiene la ventaja de ser más fácil de usar en muchos casos. Encontrar la mejor curva de ajuste con solver tiene la ventaja de mostrar lo que entendemos por mejor ajuste. También funcionará con modelos que quizás no hayan sido programados en la herramienta Trendline.

clase=”

Ejercicios: Una introducción al solucionador

En Ejercicio se$3.5.1–3.5.7$ le da una función y un intervalo se define sobre:

Hacer un gráfico de valores y trazar una gráfica de la función.
Encuentra cualquier raíz para la función.
Encuentra máximos y mínimos relativos para la función. (Recuerde incluir los puntos finales.).
Encuentra el máximo y mínimo absoluto de la función en el intervalo.

Ejercicio 1:

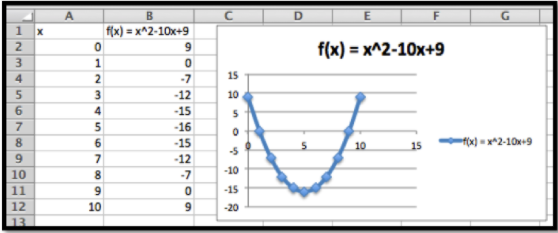
$f(x)=x^2-10x+9\text{,}$en el intervalo$0\le x\le 10\text{.}$

Contestar

$clipboard_ef622367f32ad37a45737fed1ba820b6e.png$