4.4: Diferenciación mediante álgebra computacional
- Page ID
- 115968
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Como señalamos en el capítulo 1, en este libro nos estamos limitando a herramientas matemáticas que el estudiante puede esperar razonablemente encontrar en un ambiente de trabajo genérico. Esa es una de las razones para enfocarse en el uso de hojas de cálculo y Excel. Sin embargo, también veremos el uso de herramientas web gratuitas, particularmente como un medio de hacer manipulación simbólica. La diferenciación es una de esas operaciones que se pueden realizar con herramientas gratuitas disponibles en la web. Se esperará que el alumno de este curso haga rutinariamente diferenciación simbólica a mano. No obstante, es bueno poder revisar tu trabajo. También queremos herramientas que funcionen de manera confiable con problemas más desordenado.
Al trabajar con derivados, hemos analizado tres problemas básicos:
- Dada una función, encontrar una fórmula para su derivada. Esto corresponde a encontrar la función marginal.
- Dada una función, encuentra el valor de la derivada en un punto determinado. Esto lo hacemos cuando queremos una tasa de cambio en un punto determinado.
- Dada una función, encuentra donde la derivada es 0. Esto lo hacemos cuando estamos tratando de encontrar valores mínimos o máximos de la función.
Hay una serie de sitios web que tomarán derivados simbólicos. Comenzamos con Wolfram|Alpha, que está disponible en http://www.wolframalpha.com.
: Utilice Wolfram|Alpha para encontrar la derivada de\(x^3+5x+7\text{.}\)
Solución
Cuando llamas al sitio web, obtienes una barra de entrada tanto como lo harías con tu motor de búsqueda favorito.


La interfaz para Wolfram|Alpha es bastante robusta. Podemos hacer la pregunta en inglés sencillo. En nuestro caso nos gustaría encontrar la derivada de x^3+5x+7 con respecto a x. Algunas de las formas de hacer esa pregunta son:
- encontrar la derivada de (x^3+5x+7)
- encontrar la derivada de (x^3+5x+7) con respecto a x
- derivada de (x^3+5x+7)
- diferenciar (x^3+5x+7) con respecto a x
- diferenciar (x^3+5x+7)
- D (x^3+5x+7)
- d/dx (x^+5x+7)
- (x^3+5x+7) '
Para todos estos, el sitio web proporciona la misma respuesta.
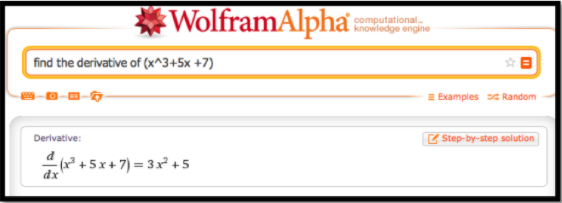
Tenga en cuenta que la respuesta nos dice la pregunta que Wolfram|Alpha está respondiendo. Esto nos ayuda a comprobar que hemos sido entendidos correctamente.
Vale la pena señalar que Wolfram|Alpha tiene la opción de mostrar soluciones paso a paso.


Wolfram|Alpha entiende la convención de que la variable para problemas matemáticos es típicamente x Si no especificamos la variable con respecto a la que estamos diferenciando, adivinará que x es nuestra variable. Otras letras se tratan como constantes a menos que usemos notación de función con paréntesis. Así podemos usar Wolfram|Alpha para verificar nuestras reglas de diferenciación.
Utilice Wolfram|Alpha para recordar la regla del cociente.
Solución

Cabe señalar que Wolfram|Alpha no funcionará con nombres largos de variables como Principal o MonthlyPayment. Simplemente necesitamos cambiar las variables para trabajar con Wolfram|Alpha.
El costo de los widgets viene dado por:
\(cost=2000+10*quantity+.001*quantity^2\)
Encuentra la tasa de cambio de costo con respecto a la cantidad cuando cantidad=1000. (Estamos utilizando la derivada para estimar el costo marginal.)
Solución
Como usaremos Wolfram|Alpha, queremos convertir la ecuación para usar variables de una sola letra.
c=2000+10*q+.001*q^2.
Queremos evaluar la derivada con respecto a q cuando q=1000.

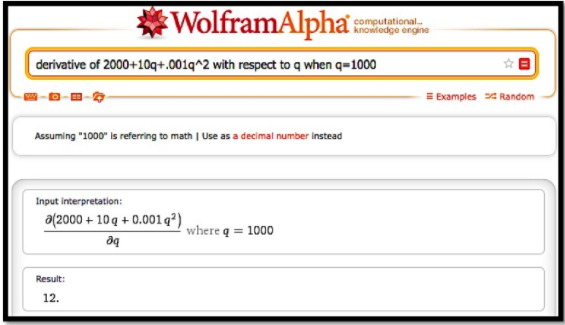
Así, cuando quantity=1000, aumentar la producción en 1 widget aumenta el costo en $12.
El tercer problema derivado básico fue encontrar un máximo o mínimo. Para problemas extremos, queremos encontrar donde la derivada es 0, ya que los extremos solo pueden ocurrir en puntos finales y puntos críticos.
Las funciones de costo y precio de demanda de los widgets vienen dadas por:
\[ cost=2000+10*quantity+.001*quantity^2 \nonumber \]
\[ revenue=\frac{100*quantity}{1+.01*quantity} \nonumber \]
Encuentra la cantidad que maximiza las ganancias.
Solución
Simplificamos los nombres de variables a q, c, p y r para cantidad, costo, beneficio e ingresos, respectivamente. Nuestra fórmula para obtener ganancias es:
\[ p=r-c=100q/(1+.01q)-(2000+10q+.001q^2 ) \nonumber \]
Al buscar un máximo, siempre empezamos por mirar una gráfica de la función en cuestión.

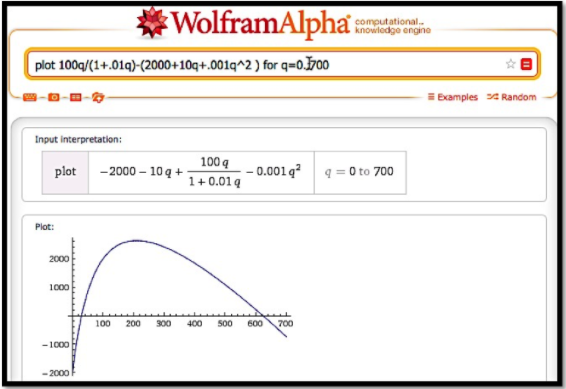
De la gráfica, queda claro que tenemos un solo máximo para la función de ganancia y se produce cerca de q=200. Para encontrar este punto, queremos tomar la derivada y ponerla igual a cero, o queremos usar el comando solve en la derivada. Entramos en el comando
solve (derivado 100q/ (1+.01q) - (2000+10q+.001q^2) con respecto a q)

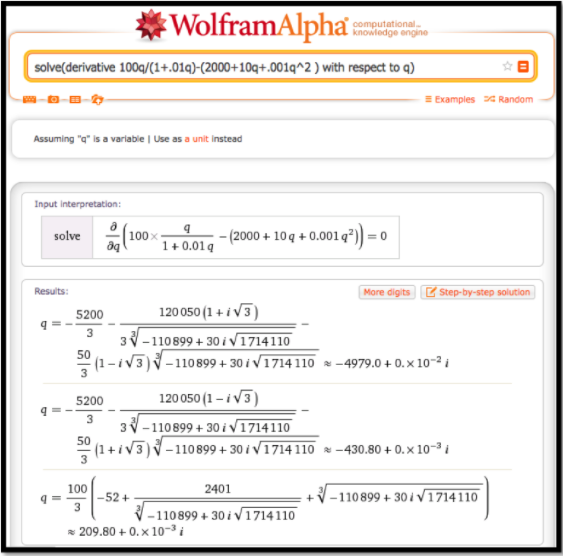
Necesitamos hacer un poco de interpretación ya que Wolfram|Alpha está usando métodos numéricos con números complejos. En particular, las respuestas tienen una parte imaginaria cero. También estamos buscando un número positivo. Por lo tanto, concluimos que la ganancia se maximiza en 209.8 widgets.
Al buscar software libre en la web para tomar derivados comenzamos con Wolfram|Alpha porque podemos usarlo a lo largo del libro cuando Excel no resuelve nuestras necesidades. También es apoyado por la compañía que produce Mathematica®, por lo que debería estar disponible en el futuro previsible. Otra fuente útil son los solucionadores de Symbolab https://www.symbolab.com/solver. Symbolab cuenta con una colección de solucionadores para los temas de este curso.

También cuenta con una sección que permite hacer ejercicio y practicar con las técnicas que hemos aprendido. Al igual que WolframAlpha, da la opción de soluciones paso a paso. Encuentro el sitio un poco más fácil de usar para los estudiantes de matemáticas.
Para problemas individuales, es posible que queramos usar otro software. Para encontrar derivados, una búsqueda rápida en la web encontró http://www.derivative-calculator.net/ lo cual es más agradable si simplemente está revisando su trabajo. Al igual que con Wolfram|Alpha, la calculadora derivada le muestra el problema en forma matemática para que pueda verificar su sintaxis.

Sin embargo, el formato de show steps es más agradable ya que al pasar el cursor sobre un paso se muestra el cambio para ese paso en la siguiente línea.


También puede encontrar otros sitios web para hacer derivados.
clase=”Ejercicios: Diferenciación mediante problemas de álgebra computacional
Para 1-12, encuentre la derivada de la función dada
\(f(x)=x \ln(x)\)
- Contestar
-
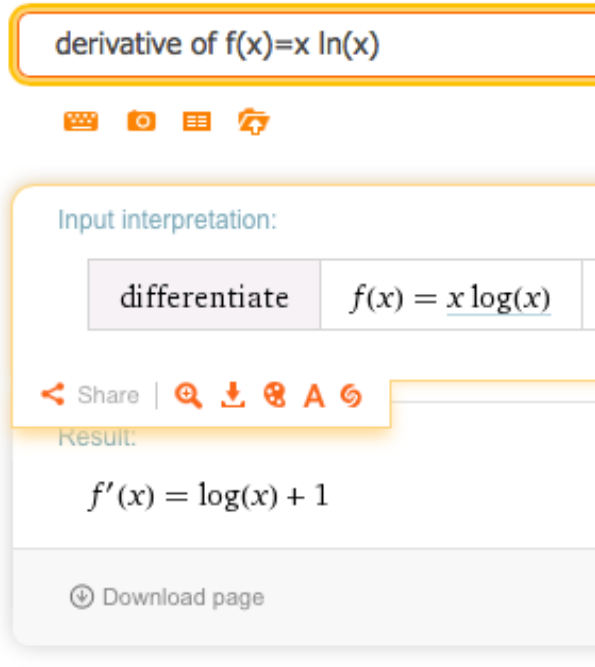

Entonces\(f' (x)= \ln(x)+1\text{.}\)
\(g(t)=e^{.07t} (-t^2+3t+5)\)
\(h(t)=t^2 e^{-0.06t}\)
- Contestar
-
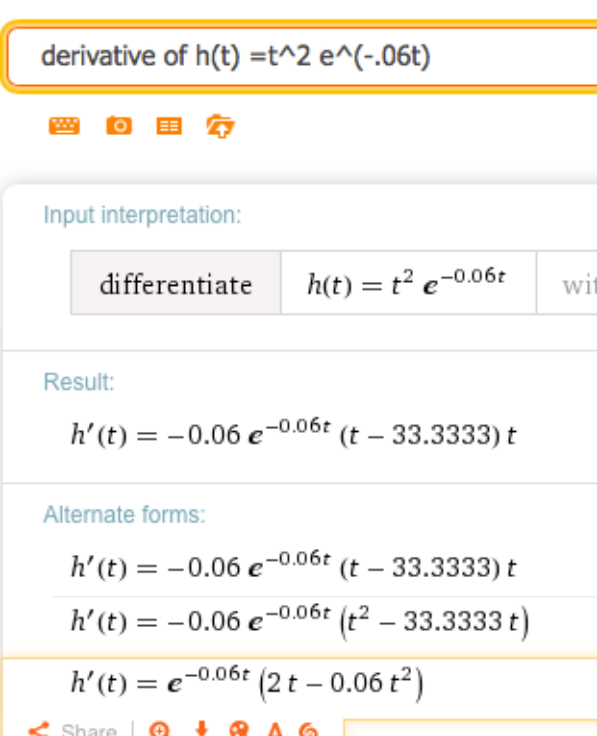

Wolfram devuelve varias formas (difieren por algún álgebra simple). Podemos elegir la que tenga la forma que nos resulte más útil. En este caso podríamos elegir por ejemplo:
\[ h' (t)=e^{-0.06t} (2t-0.06 t)^2 \nonumber \]
Es una respuesta agradable y compacta que evita aproximaciones decimales.
\(k(x)=(2x+5)^{37}\)
\(m(x)=\ln(\ln(\ln(x^2+3)))\)
- Contestar
-

Wolfram escribe ln como log pero aun así significa base que\(e\text{.}\) el log común de x sería log (10, x). Para seguir con nuestra notación diríamos
\[ m'(x)=\frac{2 x}{(x^2+3)ln(x^2+3)ln(ln(x^2+3))} \nonumber \]
Tenga en cuenta que Wolfram nos permite copiar el texto. Hoover sobre la respuesta y debajo de “A” y encontrarás texto plano que se puede copiar. Esto se puede editar en un documento Word o un documento Excel.
\(n(x)=\frac{e^x}{\ln(x^2+3)}\)
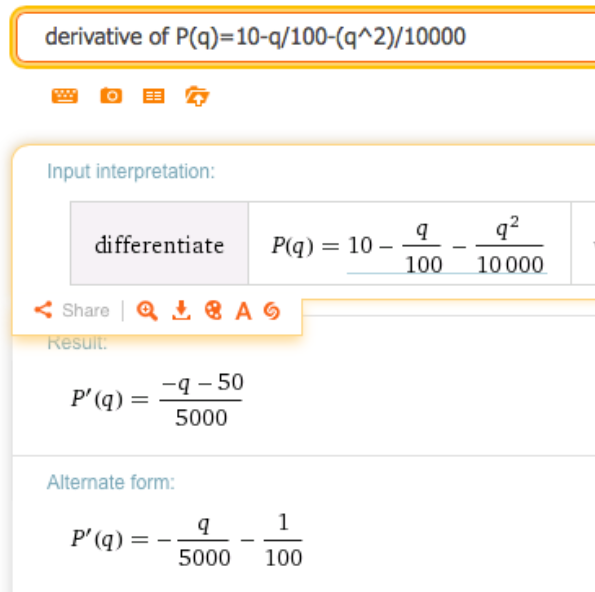
\(price=10-\frac{quantity}{100} -\frac{quantity^2}{10000}\)
- Contestar
-
Wolfram no funciona bien con variables de palabra completa. Edita la ecuación (puedes hacer esto en Wolfram) y let\(Price = P(q)\) y\(quantity = q\text{.}\) Esto da la siguiente derivada: