7.1: Aproximación de integrales definidas como sumas

Última actualización
Guardar como PDF

Page ID: 115999

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

El enfoque estándar para la acumulación es reducir el problema a un problema de área. Si dejamos que f (t) sea una función de velocidad, entonces el área bajo la curva y=f (t) entre un valor inicial de t=a y un valor de parada de t=b es la distancia recorrida en ese período de tiempo. En el caso más fácil, la velocidad es constante y usamos la fórmula simple

\[ distance = velocity * time \nonumber \]

Ejemplo 7.1.1: Distancia con Velocidad Constante.

Encuentra la distancia recorrida si voy 60 mph de 12:30 a 3:00.

Solución

Este problema es fácil de hacer sin ningún cálculo. Si graficamos la función de velocidad

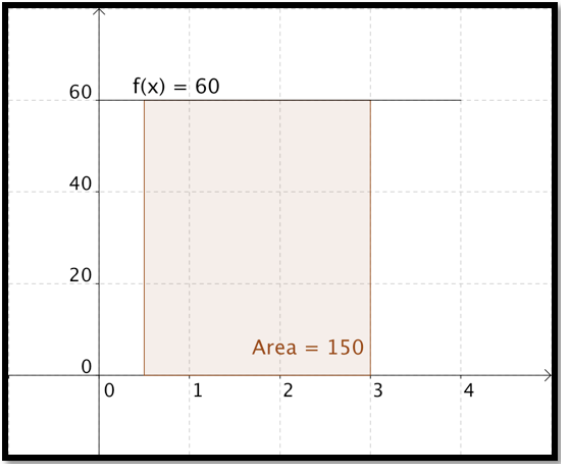
$clipboard_ef8400ed0ff057279ae8b40658a1e97e3.png$

encontramos el área del rectángulo tomando tiempos base altura y señalando$60*(3-0.5)=150\text{.}$ Tenga en cuenta que hacemos el mismo cálculo si pregunto cuánto gano en un periodo de 2.5 años si gano $60K al año, o cuánto petróleo se produce en 2 horas y media forman un pozo petrolero que produce 60 barriles de petróleo por hora.

De manera similar, si la función que estoy acumulando es lineal, puedo encontrar área usando la fórmula de área de un triángulo, una media altura de tiempo base.

Ejemplo 7.1.2: Aproximación del área bajo una función cuadrática.

La pregunta se vuelve más difícil cuando quiero encontrar el área bajo una curva que no sea lineal. Supongamos por ejemplo que queremos encontrar el área bajo la curva

\[ y = x * (4-x) \nonumber \]

entre x=0 y x=4.

Solución

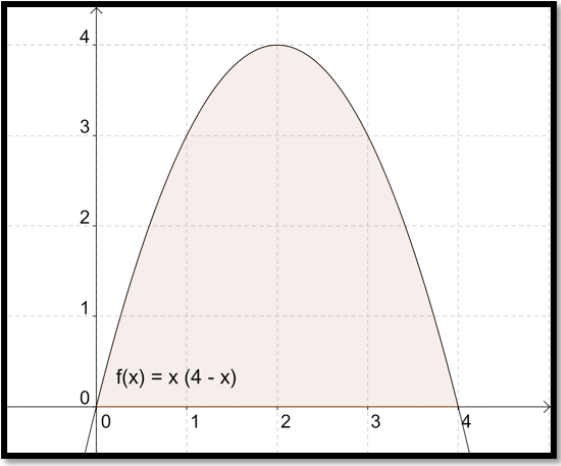
$clipboard_ee3a533c53ab2b7dc3901759e5f663ecb.png$

Ya no tenemos una fórmula agradable a partir de la geometría para la zona. Así comenzamos a hacer aproximaciones. La aproximación más fácil es señalar que el área tiene que ser menor que el área del rectángulo de 4 por 4 que podamos dibujar alrededor de la región.

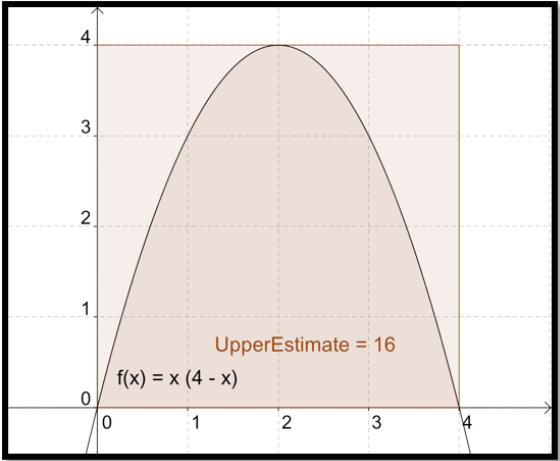
$clipboard_e30dffbb6b3117c0205767c7f97545adf.png$

Podemos mejorar nuestra estimación dividiendo el intervalo [0, 4] en 4 subintervalos iguales y luego tomando el área combinada de los 4 rectángulos que necesitamos para contener la región. Esto reduce nuestra estimación superior de 16 a 14.

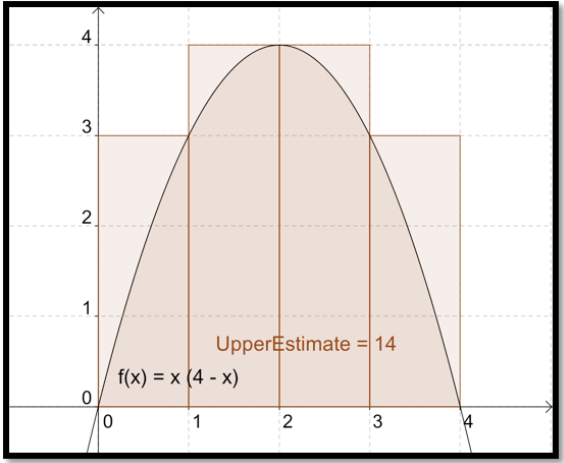
$clipboard_e7c0218e610105fe845dc161cd1276285.png$

De igual manera podríamos obtener una mejor estimación observando 8 subintervalos y viendo que el área debajo de la parábola no es superior a 12.5

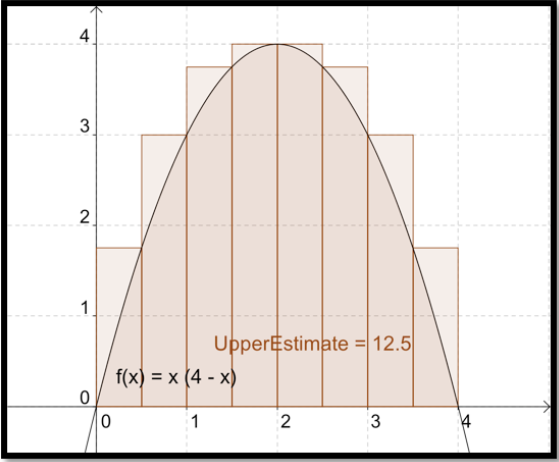
$clipboard_eb859d497bf92bb58ae6027353e63e7e0.png$

Si continuamos el proceso con 100 subintervalos, nuestra estimación se reduce a 10.83. A partir de la imagen, parece una estimación bastante buena.

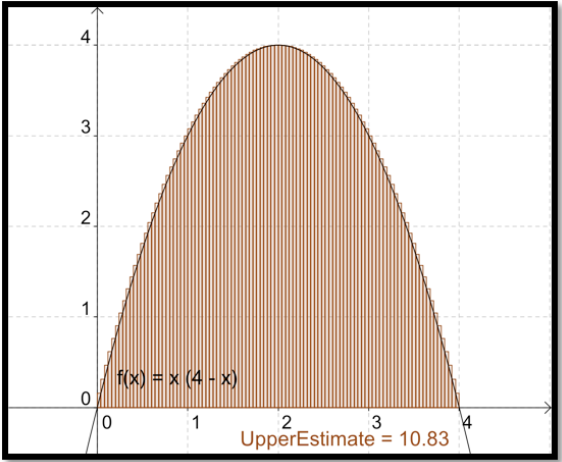
$clipboard_ee0feb074bdb1b3fefd967446f465fda3.png$

Podemos cambiar el número de subdivisiones con el interactivo a continuación.

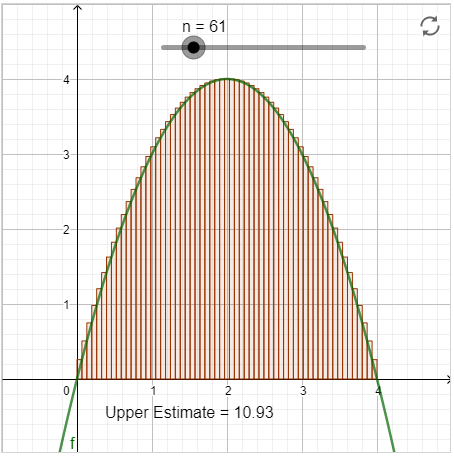
$clipboard_e63c143f560c7e6760710da75f57c6623.png$

Figura$7.1.3.$ GeoGebra: Aproximación de la suma superior

Si bien este proceso sería muy largo y tedioso a mano, el proceso de encontrar el área de cada uno de los 100 rectángulos y agregar las áreas es bastante fácil en Excel. Antes de ir a Excel, queremos hacer un pequeño ajuste en nuestro método. El método que utilizamos siempre da una sobreestimación. También requiere que sepamos donde la función alcanza un máximo en cada subintervalo. Será más fácil si estimamos el área tomando siempre la altura del rectángulo en el extremo derecho del subintervalo. Con 4 subintervalos esto da una estimación de 10 para nuestra área.

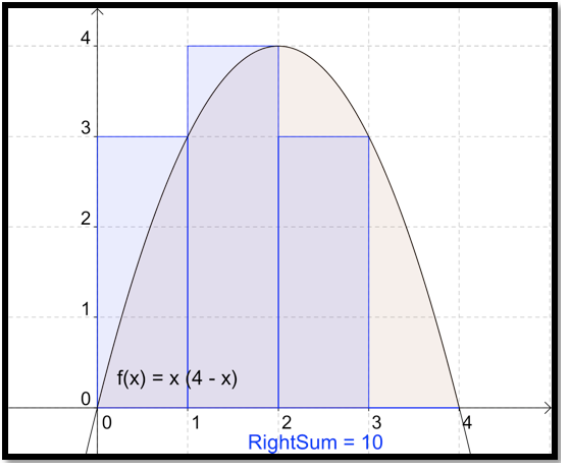
$clipboard_e6631d17add612ac30426a3973403144d.png$

Cuando aumentamos el número de subintervalos a 100, una vez más obtenemos una estimación bastante buena del área. A partir de la imagen, es difícil ver diferencia entre el área definida por la curva y el área definida por los rectángulos.

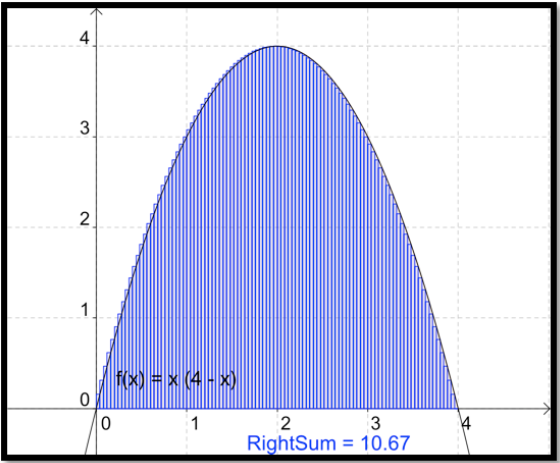
$clipboard_e7eb7a40fb840f335b885805efa022b81.png$

Ejemplo 7.1.4:

Encuentra el área bajo la curva$y=x*(4-x)$ con$x$ entre 0 y 4 con Excel

Solución

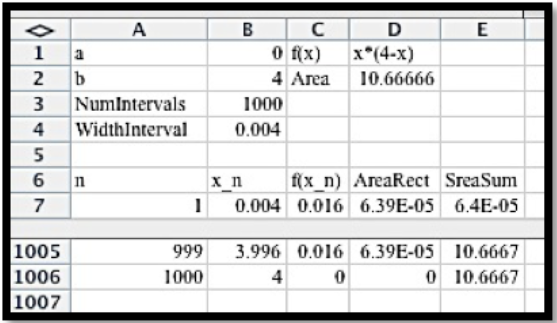
Aproximaremos el área con 100 rectángulos. Configuramos una hoja de trabajo para encontrar el área del primer rectángulo.

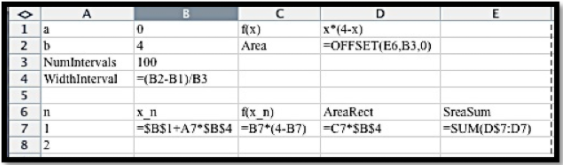
$clipboard_ea97fde5111ef5898208966a6ea7675d0.png$

Siguiendo nuestra práctica estándar, configuramos la pregunta y la respuesta en áreas etiquetadas en la parte superior de la hoja de trabajo. El ancho de un subintervalo es el ancho de todo el intervalo dividido por el número de subintervalos. La columna$x_n$ es para el valor x en el lado derecho del n-ésimo subintervalo. El valor de$x_n$ es el punto de partida más n veces el ancho de un subintervalo. Luego evaluamos la función en$x_n\text{.}$ El área del n-ésimo rectángulo es la altura, o$f(x_n)\text{,}$ veces el ancho del subintervalo. La última columna es el área total para los primeros n rectángulos. El área para 100 rectángulos es nuestra estimación de área.

Para encontrar el área llenamos rápidamente nuestra hoja de trabajo.

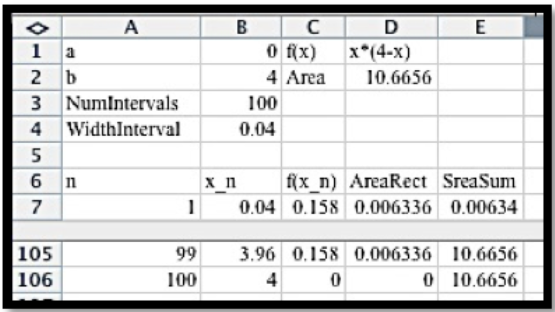
$clipboard_e48f60bd0afe42dce211f22cc6409d61c.png$

Para una estimación más precisa dividimos en rectángulos más pequeños.

$clipboard_e36529e9da2ec3950601c60e50c8f7c74.png$

Si bien 100 subintervalos estarán lo suficientemente cerca para la mayoría de los problemas que nos interesan es, el “área”, o integral definida se definirá como el límite de esta suma ya que el número de subintervalos va al infinito. Por lo tanto

\[ \int_a^bf(x) dx=\lim_{n\to \infty} \sum_{i=1}^nf (x_i)\Delta x \nonumber \]

con$\Delta x=\frac{b-a}{n}$ y$x_i=a+i*\Delta x\text{.}$

Las sumas de la forma,$\sum_{i=1}^n f(x_i)\Delta x$ con$\Delta x=\frac{b-a}{n}$ y$x_i=a+i*\Delta x\text{,}$ se llaman sumas de Riemann. El límite, escrito$\int_a^bf(x) dx\text{,}$ se llama integral definida.

Como ayuda de memoria, vale la pena señalar que el símbolo utilizado para la suma es una sigma mayúscula, o S para suma en el alfabeto griego. Cuando tomamos el límite utilizamos un signo integral, que es una S estilizada en el alfabeto latino.

Vale la pena señalar que en esta definición estamos encontrando “área señalizada bajo una curva”. Si la función$f(x)$ es negativa a lo largo del intervalo, la integral también será negativa, en la misma tendríamos un cambio negativo en nuestro extracto bancario si estuviéramos retirando dinero de manera constante. De igual manera podemos obtener una integral negativa cuando se invierten los extremos del intervalo. Si estoy constantemente agregando dinero a una cuenta, el cambio neto es negativo si mido desde 5 años en el futuro hasta hoy.

Debemos señalar que, para funciones lo suficientemente agradables como para ser consideradas en esta clase, llegamos al mismo límite mediante el uso de rectángulos con la función evaluada en el lado derecho del rectángulo o el lado izquierdo del rectángulo, o cualquier punto del rectángulo que elijamos. Elegir el lado derecho para la evaluación hace que nuestras fórmulas sean un poco más simples.

Ejemplo 7.1.5: Valor Presente de un Flujo de Ingresos.

El valor actual estimado del flujo de ingresos, en miles de millones de dólares, de una empresa que se compra es$f(x)=\exp(-0.06*x)*0.235\text{.}$ El valor presente de ese flujo de ingresos es el área de la región bajo la curva$y=f(x)$ de$x=0$ a$x=15\text{.}$ Usar 500 intervalos para estimar el valor presente.

Solución

Aunque los datos en la pregunta para este ejemplo son bastante diferentes del ejemplo anterior, la configuración de la hoja de trabajo para evaluar la suma de Riemann es la misma.

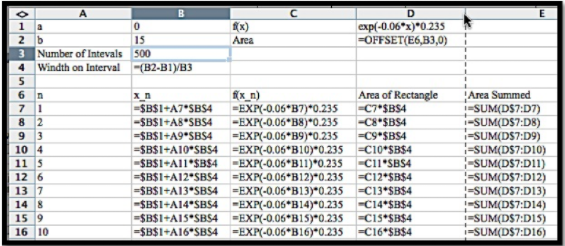
$clipboard_e69aab58f23683634e5644e947c881a1f.png$

Con 500 intervalos estimamos que el valor actual del flujo de ingresos valdrá 2.3222 mil millones de dólares. Si solo hubiéramos usado 100 intervalos, la estimación habría sido de $2.318 mil millones, mientras que 1000 intervalos da una estimación de $2.3232 mil millones.

Ejercicios: Aproximación de Integrales Definidas como Problemas de Sumas

Ejercicio 1:

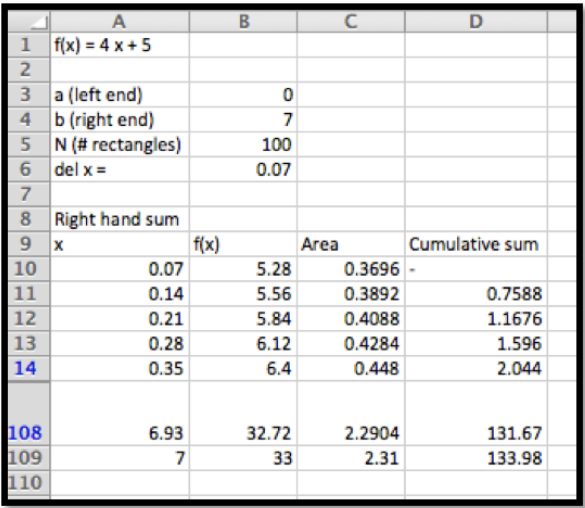
Deje$f(x) = 4 x + 5\text{.}$ Estimar el área debajo$f(x)$ en el intervalo$0 \le x \lt 7$ usando 100 rectángulos y una regla de mano derecha.

Contestar: Los comandos de Excel son:

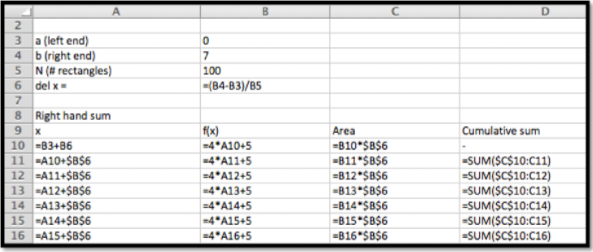
$clipboard_e207adfbe5ec595c9f9e8ae2e3b58dc64.png$

La respuesta se da de la siguiente manera. Tenga en cuenta que en esta captura de pantalla la parte central del lado lateral estaba oculta para que la imagen sea de un tamaño razonable

El área es aproximadamente 133.98

$clipboard_e69aef8ca4312d6104695bcd7512d018c.png$