7.2: El teorema fundamental del cálculo
- Page ID
- 116000
En la última sección definimos la integral definida,\(\int_a^b f(t)dt\text{,}\) el área señalizada bajo la curva\(y= f(t)\) de\(t=a\) a\(t=b\text{,}\) como el límite del área encontrada al aproximar la región con rectángulos cada vez más delgados. También vimos que podemos encontrar fácilmente una aproximación razonable al área usando Excel para encontrar tal suma con un número bastante grande de rectángulos.
En el caso trivial donde tenemos una función constante\(f(t)=c\) podemos encontrar el área del área con una fórmula simple,\(\int_a^b c\ dt=c(b-a)=cb-ca\text{.}\) Si definimos una función de área,\(F(x)\text{,}\) como el área bajo la curva\(y=f(t)\) desde\(t=0\) hasta\(t=x\text{,}\) entonces la función de área en este caso es\(F(x)=c*x\text{.}\) Nos gustaría para poder evaluar más integrales con un proceso como este, donde tenemos una función de área simple.
Pasamos la variable independiente de\(t\) para la función\(f\) a\(x\) para la función\(F\) porque tenemos dos variables independientes en nuestra discusión y queremos mantenerlas separadas para evitar confusiones. Consideraremos\(f\) como una función de\(t\text{,}\) y queremos encontrar el área bajo la gráfica de\(f(t)\text{.}\) Consideraremos\(F\) como una función de\(x\text{,}\) y entenderla como el área bajo la curva\(y=f(t)\) desde algún punto de partida\(t=a\) hasta\(t=x\text{.}\)
Comenzamos explorando casos donde podemos justificar una función de área sin usar cálculo. Luego veremos algunos casos en los que podemos verificar experimentalmente la función de área con Excel. Finalmente daremos la regla general para la función de área, el Teorema Fundamental del Cálculo, y daremos alguna justificación.
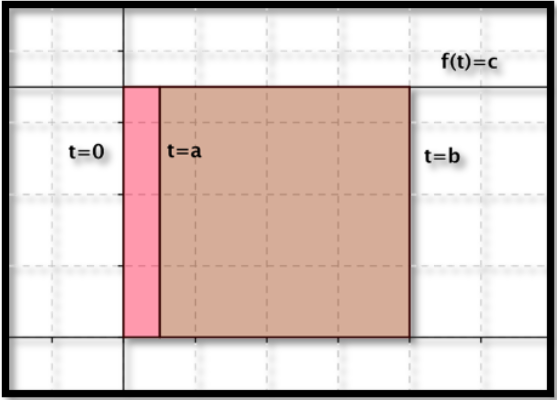
Dejar\(f(t)=c\text{.}\) Para una función constante,\(f(t)=c\text{,}\) el área bajo la curva será el área de un rectángulo de alto\(c\) y ancho\(b-a\text{.}\) La función de área obvia es\(F(x)=c*x\text{.}\)
Solución
Entonces
\[ \int_a^b c dt=F(b)-F(a)=c*b-c*a=c(b-a). \nonumber \]
Vale la pena señalar que esta fórmula da “área firmada”. Si c o b-a es negativo, el “área” es negativa.
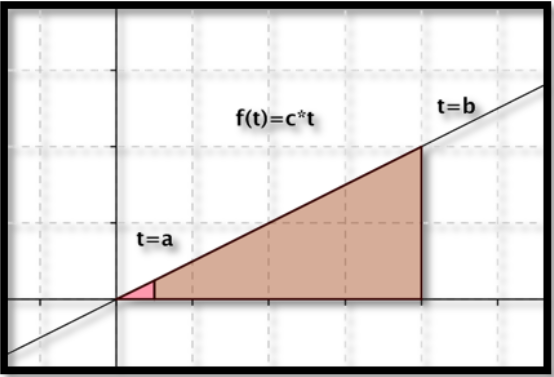
Let\(f(t) = c*t\text{.}\) Para una función lineal,\(f(t) = c*t\text{,}\) el área bajo la curva de 0 a\(b\) será el área de un triángulo de alto\(c*b\) y ancho\(b\text{.}\)

Solución
La función de área obvia es\(F(x)=c*x^2/2\text{.}\) Si también\(a\) es distinta de cero, el área es la diferencia de las áreas de dos triángulos.
\[ \int_a^b c*t dt=F(b)-F(a)= \frac{c*b^2}{2}-\frac{c*a^2}{2}=\frac{c (b^2-a^2 )}{2}. \nonumber \]
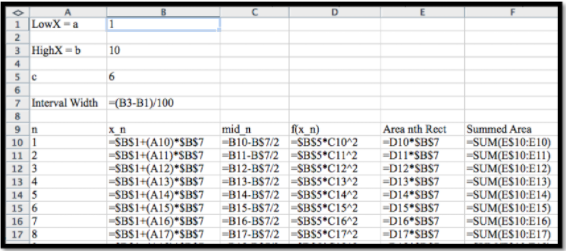
Como consideramos encontrar área con sumas de Excel y Riemann, en lugar de usar una regla de la derecha para los rectángulos, vamos a usar una regla de punto medio donde encontramos el área de rectángulos evaluados a la mitad de cada intervalo.

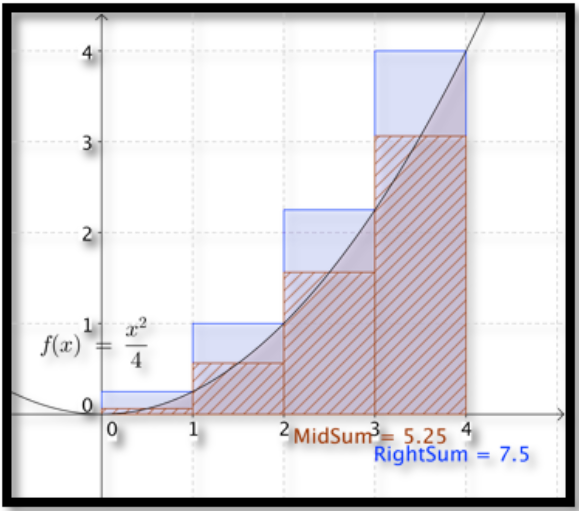
La regla de la derecha usa una fórmula más fácil, así que la usamos primero. Para el i-ésimo rectángulo evaluamos en\(x_i=a+i\Delta x\text{.}\) Para la fórmula de punto medio, evaluamos en el punto medio del intervalo, en\(mid_i=a+i\Delta x-\Delta x/2\text{.}\) Como sugiere la imagen, la fórmula de punto medio da una mejor aproximación. La regla de la derecha siempre sobreestima una función creciente. La regla de punto medio es exacta para funciones lineales donde el punto medio es el valor promedio.
En ambos ejemplos hemos examinado la función area tiene como derivada la función original. Nos gustaría usar Excel para probar algunos casos más. En las hojas de trabajo que configuramos en la última sección, SuMarea es la función de área que estamos buscando. Trazaremos la función de área y usaremos una curva de mejor ajuste para encontrar la ecuación de la función de área.
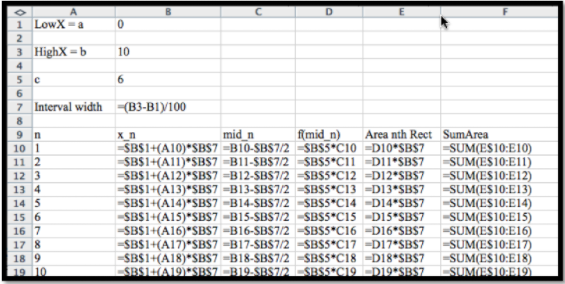
Repita el último ejemplo, encontrando el área debajo\(f(x)=6x\text{,}\) con Excel. Con una función lineal hemos utilizado lo siguiente para producir una función de área.

Solución
La columna C tiene nuestra lista de\(t\) valores en el centro de cada intervalo. La columna D tiene el valor de\(f(t)\) evaluado en esos puntos. El área del rectángulo es la altura\(f(mid_n)\) por el ancho, Ancho de intervalo. SuMarea es nuestra función de área de carrera. Cuando trazamos la función de área tenemos algo que parece ser cuadrático con coeficiente inicial\(c/2\) y coeficientes lineales y constantes muy pequeños. De hecho los coeficientes lineales y constantes son cero hasta un factor de redondeo para números del tamaño que estamos usando.

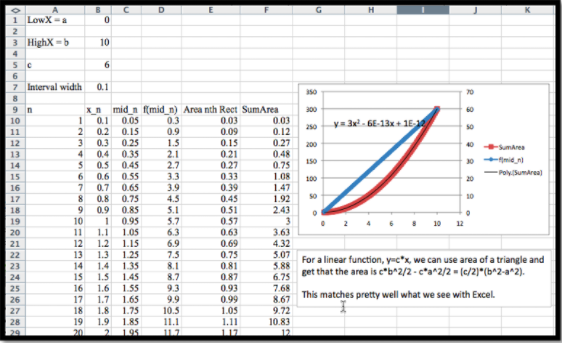
Esto coincide con el resultado que tuvimos resolviendo el problema con la geometría. Sin embargo, podemos repetir el proceso con Excel y usar funciones de orden superior.
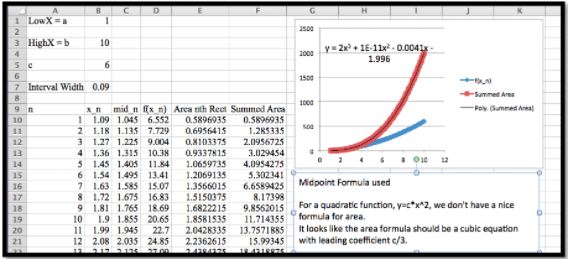
Encuentra la función de área cuando\(f(t) = 6t^2\text{.}\)
Solución
Para este problema esencialmente repetimos el trabajo del ejemplo anterior con una función cuadrática para\(f(t)\text{.}\)

Cuando trazamos la función de área obtenemos un ajuste muy bueno con una función cúbica. Una vez más, permitiendo la forma en que las curvas de mejor ajuste pueden devolver pequeños valores aleatorios para coeficientes que deberían ser cero, vemos que si\(f(t) =c*t^2\text{,}\) entonces la función de área relacionada es
\[ F(x)=c*t^3/3\text{.} \nonumber \]

Encuentra el área cuando\(f(x)=6 x^3\text{.}\)
Solución
Una vez más, podemos usar Excel para producir una función de área. La función de área parece ser\(F(x)=1.5 x^4\text{.}\)

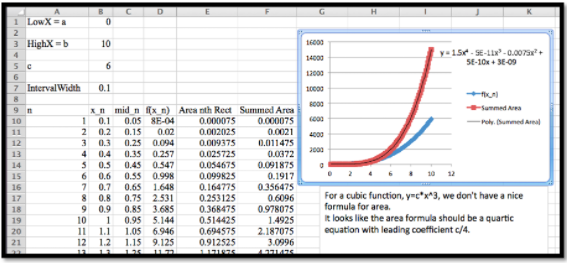
En todos los ejemplos anteriores observamos que la función area,\(F(x)\text{,}\) tiene\(f(x)\text{,}\) la curva que estamos encontrando el área bajo, como su derivada. Así, en estos casos, el área es un anti-derivado de\(f(x)\text{.}\) Esta observación generaliza al Teorema Fundamental del Cálculo, el cual tiene dos versiones:
Dejar\(f(x)\) ser una función continua en el intervalo\([a, b]\text{.}\) En ese intervalo definir una función de área por\(F(x)=\int_a^x f(t) dt\text{.}\) Entonces\(\frac{d}{dx} F(x)=f(x)\text{.}\)
Dejar\(f(x)\) ser una función continua en el intervalo\([a, b]\text{.}\) Supongamos que\(F(x)\) es cualquier función continua, diferenciable con\(\frac{d}{dx} F(x)=f(x)\text{.}\) Then\(\int_a^b f(t) dt=F(b)-F(a)\text{.}\)
En la práctica utilizamos la segunda versión del teorema fundamental para evaluar integrales definidas. Encontramos una función\(F(x)\) cuya derivada es el integrando\(f(x)\) y luego evaluamos\(F(x)\) en los puntos finales. Es más fácil probar o justificar la primera versión del teorema fundamental. El argumento básico señala que es\(F(x)=\int_a^xf(t) \ dt\text{,}\) entonces formalmente
\[ \frac{d}{dx} F(x)=\lim_{h\to 0} \frac{(F(x+h)-F(x))}{h}. \nonumber \]

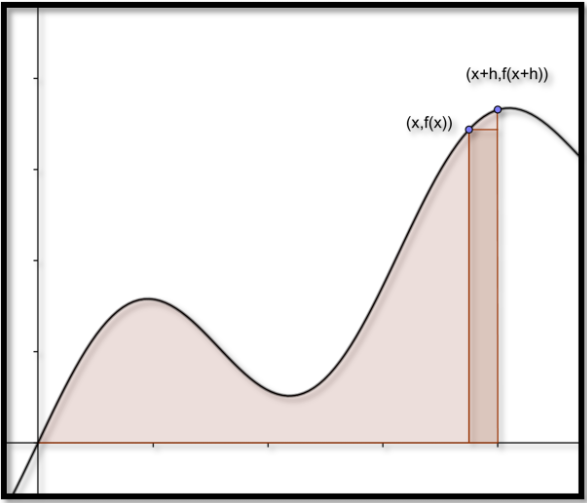
Pero si\(h\) es pequeño,\(F(x+h)-F(x)\) es aproximadamente el área de un rectángulo de altura\(f(x)\) y con\(h\text{,}\) ello el\(F'(x) = f(x)\text{.}\) Observamos entonces que cualesquiera dos antiderivados de una función difieren por una constante.
En el ejemplo 7.1.4 de la sección anterior, utilizamos sumas de Riemann con intervalos de 100 y 1000 para aproximar el área inferior\(y = x*(4-x)\) con\(x\) entre 0 y 4. Encontrar el área usando el teorema fundamental del cálculo,
Solución
Reescribimos la curva como\(f(x) = 4x – x^2\) y notamos que una anti-derivada de\(f(x)\) es\(F(x) = 2 x^2 - x^3/3\text{.}\) Entonces
\[ \int_0^4 f(x)\ dx=F(4)-F(0)=\left(32-\frac{64}{3}\right)-(0)=10 \frac{2}{3}. \nonumber \]
Para obtener la misma respuesta a 4 decimales, necesitábamos usar 1000 intervalos con sumas de Riemann. Claramente, es más fácil resolver este problema con el teorema fundamental del cálculo que hacer una aproximación con tantos intervalos.
Vamos\(f(x)=x^2 e^{-x}\text{.}\) Nos dicen\(F(x)=(x^2+2 x+2) (-e^{-x})\) es un anti-derivado de\(f(x)\text{.}\) Verificar el anti-derivado y encontrar el área bajo la curva con\(x\) entre 0 y 2.
Solución
Usando la regla del producto,
\[ F'(x)=(2x+2) (-e^{-x}) + (x^2+2x+2) (e^{-x})=x^2 e^{-x}=f(x) \nonumber \]
El área es
\[ F(2) – F(0) = 10(-e^{-2}) – 2(e^{0}) = -2 – 10/e^2 = -3.3534 \nonumber \]
También queremos revisitar nuestros tres primeros ejemplos a la luz del teorema fundamental si el cálculo. En todos esos ejemplos utilizamos Excel para encontrar una curva que mejor se ajuste a una función de área. Ahora podemos verificar nuestro trabajo tomando la derivada, ajustando los parámetros según sea necesario para encontrar un anti-derivado. Para funciones constantes y lineales ya hemos hecho el ajuste porque pudimos encontrar la función de área a partir de la geometría.
Ejemplo 3a: Encuentra la función de área cuando\(f(t) = 6t^2\text{.}\)
Solución
Ya hemos usado Excel para encontrar una curva que mejor se ajuste.

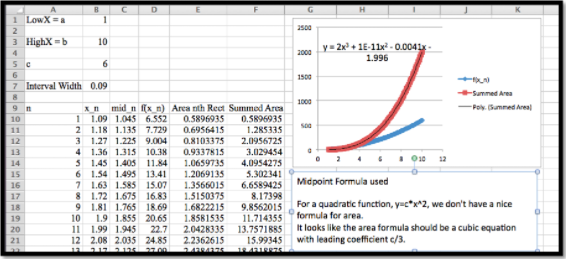
Por lo tanto, sospechamos que el anti-derivado debe ser un polinomio cúbico. Necesitamos
\[ 6t^2=d/dt (at^3+bt^2+ct+d)=3at^2+2bt+c. \nonumber \]
Estableciendo coeficientes iguales para cada potencia, vemos\(a = 2\) y\(b = c = 0\text{.}\) así nuestra función de área tiene la forma\(F(t) = 2 t^3 + d\text{.}\) Dado que\(F(0)\) es el área de una región entre\(t = 0\) y\(t = 0\text{,}\) concluimos\(d = 0\) y nuestra función de área es\(F(t) = 2 t^3\text{.}\)
Encuentra el área cuando\(f(x) = 6 x^3\text{.}\)
Solución
Usando Excel adivinamos la función de área Ahora\(F(x) = 1.5 x^4\text{.}\) podemos verificar que la derivada de\(F(x)\) es\(f(x)\text{,}\) así que hemos encontrado una anti-derivada.
Cabe señalar que el uso del teorema fundamental para evaluar integrales requiere que seamos capaces de encontrar un anti-derivado de una función. Encontrar un anti-derivado puede ser bastante difícil o incluso una tarea imposible. El método que acabamos de usar a menudo se conoce como el método de “adivinar y verificar” para encontrar antiderivados. Analizaremos los métodos para encontrar antiderivados en las siguientes secciones.
clase=”Ejercicios: El teorema fundamental de los problemas de cálculo
Vamos Se\(f(x) = 4 x + 5\text{.}\) nos dice que\(F(x) = 2 x^2 + 5 x + 7\) es un anti-derivado.
- Verificar que\(f(x)\) sea un derivado de\(F(x)\text{.}\)
- Utilizar el teorema fundamental del cálculo para evaluar\(\int_1^5 f(x)\ dx\text{.}\)
- Aproximado\(\int_1^5 f(x)\ dx\text{,}\) usando sumas de Riemann y 100 intervalos.
- Contestar
-
- \[ F' (x)=\frac{d}{dx} (2 x^2+ 5 x + 7)=4x+5 \nonumber \]


