7.8: Aplicaciones Económicas de lo Integral

Última actualización
Guardar como PDF

Page ID: 115986

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Hemos visto la integral definida como el área señalizada bajo una curva. Esto nos permite calcular el beneficio total, o ingresos, o costo, a partir de las funciones marginales relacionadas. Hemos analizado una serie de aplicaciones donde esto se interpretó como una acumulación a lo largo del tiempo, incluyendo la producción total de un pozo petrolero y el valor actual de una corriente de ingresos. Para algunas aplicaciones queremos mirar el área entre dos curvas. Por ejemplo, considerando la ganancia como el área entre las curvas de costo e ingresos.

En esta sección veremos más aplicaciones desde finanzas y economía donde los conceptos se pueden describir fácilmente en términos como del área entre curvas.

Excedente de consumo y productor

Cuando miramos las curvas de oferta y demanda encontramos un punto de equilibrio donde la cantidad que se ofrecía a la venta era igual a la cantidad que la gente quería comprar.

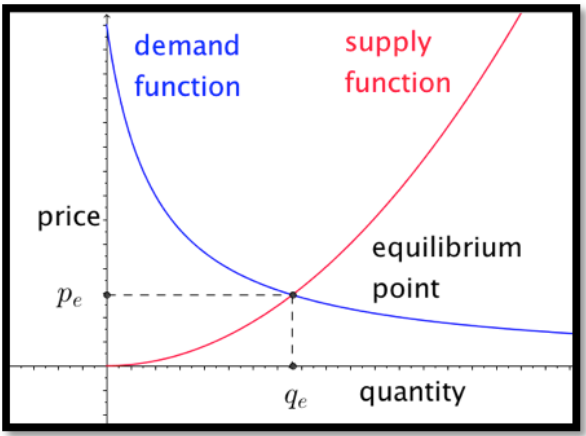
$clipboard_e0f93745059c91883d334a509b0a6b083.png$

No obstante, en ese modelo, había gente que estaba dispuesta a vender por menos del precio de equilibrio y gente que estaba dispuesta a comprar por más que el precio de equilibrio. Estas personas consiguieron un trato excepcionalmente bueno en la transacción. Nos gustaría medir ese beneficio, ya que podemos pensarlo como el beneficio extra que obtienen los proveedores y compradores en la transacción. Observamos que cada lado tendrá un incentivo para maximizar ese beneficio.

Centrarse primero en el lado del consumidor. El área bajo la función demanda, desde 0 hasta la cantidad vendida, mide la disposición de los consumidores a gastar. El área en el rectángulo con esa misma base y altura igual al precio de venta mide el gasto real del consumidor. La diferencia entre los dos es una cantidad que llamaremos excedente de consumo.

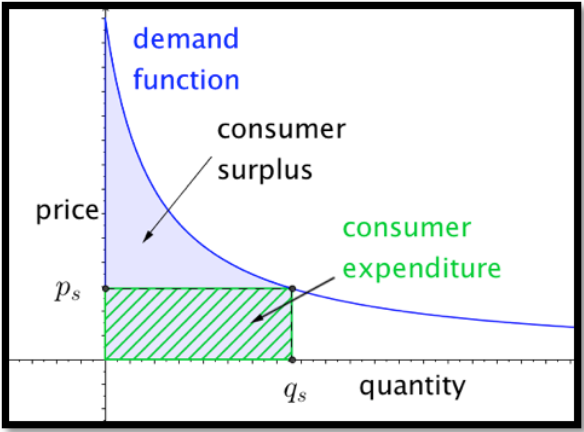
$clipboard_e87af2798355b48549a06a70b0f8ec7a7.png$

En términos de cálculo:

\[ Willingness\ To\ Spend= \int_0^{q_s} demand\ function(q) dq \nonumber \]

\[ consumer\ expendature= \int_0^{q_s} p_s dq \nonumber \]

\[ consumer surplus= \int_0^{q_s} (demand\ function(q)- p_s ) dq \nonumber \]

Mientras el precio permanezca en la curva de función de demanda, un precio menor significa una mayor cantidad vendida y un mayor superávit del consumidor.

De manera similar, podemos enfocarnos en el lado productor. El área bajo la función de suministro, desde 0 hasta la cantidad vendida, mide la necesidad de ingresos de los productores. El área en el rectángulo con esa misma base y altura igual al precio de venta mide los ingresos reales del productor. La diferencia entre los dos es una cantidad que llamaremos excedente productor.

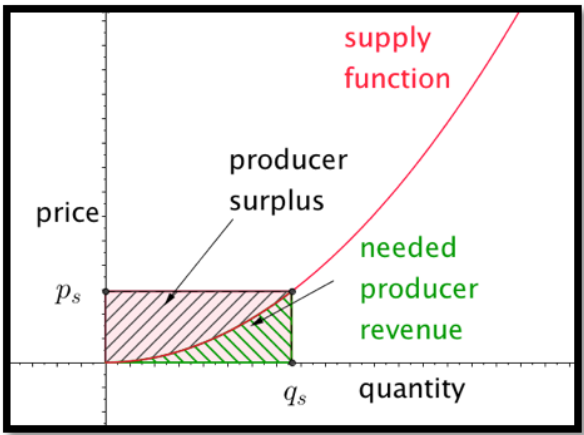
$clipboard_ed44f72a11a26179fd14a9b194aebe400.png$

En términos de cálculo:

\[ Needed\ revenue= \int_0^{q_s} supply function(q) dq \nonumber \]

\[ producer\ revenue= \int_0^{q_s} p_s dq \nonumber \]

\[ producer\ surplus= \int_0^{q_s} ( p_s-supply function(q)) dq \nonumber \]

Mientras el precio permanezca en la curva de función de oferta, un precio más alto significa una mayor cantidad vendida y un mayor superávit del productor. Consideremos primero un ejemplo donde las funciones de oferta y demanda son lo suficientemente simples como para que todos los cálculos se puedan hacer a mano.

Ejemplo 7.8.1: Excedente de Productor con Funciones Lineales.

Estoy tratando de vender widgets y he determinado que las funciones de oferta y demanda son:

\[ supply price(quantity)=4+quantity \nonumber \]

\[ demand price(quantity)=106- 2*quantity \nonumber \]

Encuentra el precio y la cantidad de equilibrio. Encuentre los excedentes de productor y consumidor cuando las playeras se vendan al precio de equilibrio. Si los productores forman un cártel, encuentren el precio que maximice el excedente del productor.

Solución

Al establecer el precio de oferta y el precio de demanda iguales entre sí, encontramos una cantidad de equilibrio de 34 y un precio de equilibrio de 38. Las fórmulas para los excedentes de consumidor y productor se convierten en:

\[ consumer surplus= \int_0^{34} ((106-2q)-38) dq \nonumber \]

\[ producer surplus= \int_0^{34} ( 38-(4+q)) dq \nonumber \]

Para evaluar las integrales podemos notar que cada una es un triángulo de base 34. Uno tiene una altura de 34 y el otro tiene una altura de 68. Usando geometría, el excedente del consumidor es de $1,156 y el excedente del productor es de 578 dólares.

Para encontrar el excedente máximo del productor, necesitamos convertir el punto final en una variable. Si los productores actúan como cártel

\[ producer\ surplus= \int_0^x ( (106-2x)-(4+q)) dq=\int_0^x ( 102-2x-q) dq \nonumber \]

\[ =\left.\left((102-2x)q-\frac{q^2}{2}\right) \right|_0^x=((102-2x)x-\frac{x^2}{2}=102x-\frac{5x^2}{2} \nonumber \]

Podemos encontrar el máximo de esto tomando su derivada y fijándola igual a 0. El máximo ocurre cuando$x=\frac{102}{5}=20.4\text{.}$ En ese punto el excedente del productor es de $1,040.40

Ahora probamos un ejemplo donde necesitamos otras técnicas para evaluar las integrales.

Ejemplo 7.8.2: Excedente de Productor con Integración Numérica.

Una tienda que intenta vender camisetas en el campus ha determinado que las funciones de oferta y demanda son:

\[ supply price(quantity)=5+\ln (quantity+10) \nonumber \]

\[ demand price(quantity)=10+100/(quantity+2) \nonumber \]

Encuentra el precio y la cantidad de equilibrio. Encuentre los excedentes de productor y consumidor cuando las playeras se vendan al precio de equilibrio.

Solución

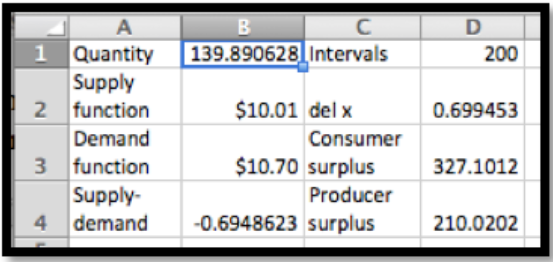
Cargamos las funciones de precio de oferta y demanda en excel y utilizamos Objetivo Buscar encontrar un precio de equilibrio. Redondeando a la unidad más cercana por cantidad y centavo por precio, tenemos un precio de equilibrio de $10.45 para una cantidad de 222 playeras.

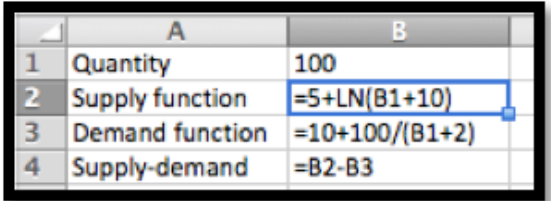
$clipboard_edaade3a35695f048480bab3f5c385f32.png$

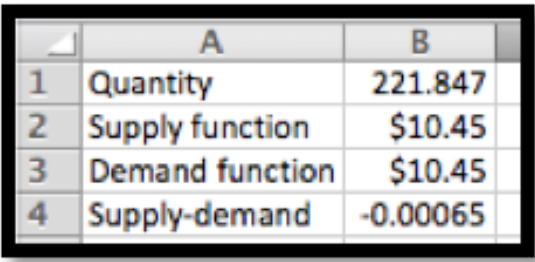
$clipboard_e90b3cc30a015caeaba805dd1d8e854d1.png$

Luego sustituimos estos valores en las ecuaciones para el excedente de consumidor y productor.

\[ consumer\ surplus= \int_0^{q_s} (demand\ function(q)- p_s ) dq \nonumber \]

\[ consumer\ surplus= \int_0^{222} ((10+100/(quantity+2))- 10.45) dq \nonumber \]

\[ producer\ surplus=\int_0^{q_s} ( p_s-supply\ function(q)) dq \nonumber \]

\[ producer\ surplus=\int_0^{222} ( 10.45-(5+\ln (quantity+10))) dq \nonumber \]

Para evaluar estas integrales utilizamos una aproximación de suma de Riemann, como la que se encuentra en la hoja de trabajo de ejemplo, o usamos Wolfram Alpha. En cualquier caso, redondeado al dólar más cercano, tenemos un superávit de consumo de 372 dólares y un excedente de productor de 191 dólares.

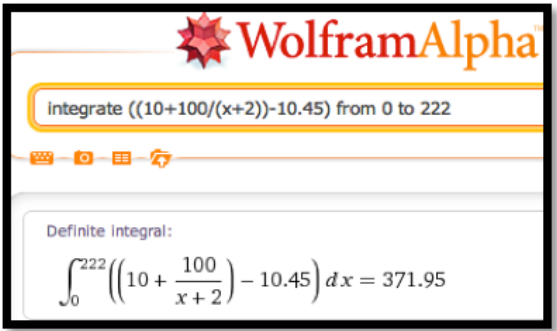
$clipboard_ebc669a7ad650c894e6956f7bd8c7b2ef.png$

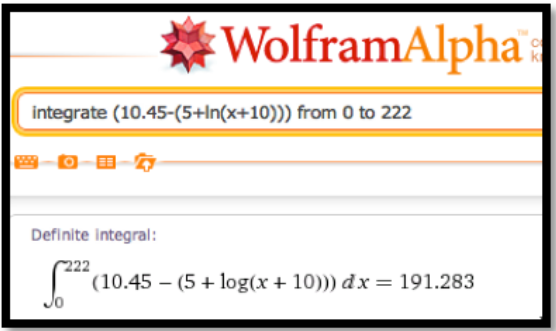
$clipboard_e5bd043222f898f9592809103b6b773dd.png$

La suma del excedente del consumidor y del excedente del productor se denomina ganancia social total. Al observar el excedente de los consumidores, asumimos que las ventas estaban determinadas por la oferta y que el punto precio-cantidad estaba en la curva de oferta. De igual manera, al observar el excedente de los productores asumimos que el precio está establecido por la demanda y el punto precio-cantidad estaba en la curva de demanda. Si ambos lados están formados por muchos individuos que actúan de manera independiente, el punto precio-cantidad es el punto de equilibrio, que está en ambas curvas. Vender en ese punto también maximiza la ganancia social total.

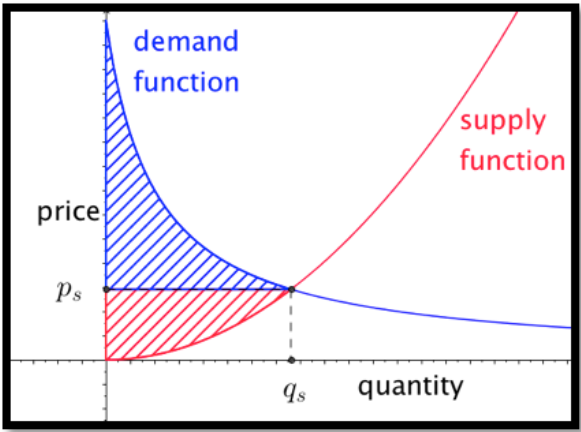
$clipboard_e88ec7da3b488e3fc2c74ac143df3afb2.png$

Sin embargo, si bien los productores o consumidores pueden organizarse y actuar como una unidad, pueden formar un cártel y limitar la cantidad vendida. Si los productores forman un cártel, pueden bajar la producción y subir el precio.

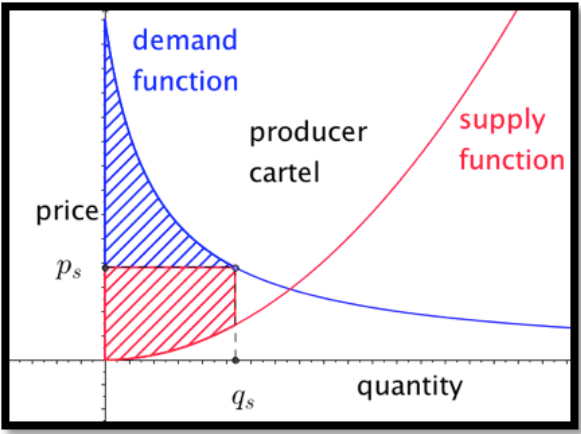
$clipboard_e22b9b4231caa4a2bd88f641f704e7699.png$

Como podemos ver en la imagen, esto siempre baja la ganancia social total. Sin embargo, para cierta reducción de cantidad se incrementa el excedente de los productores. En la ecuación para el excedente del productor el precio$p_s$ es más$demand\ function (q_s)$ bien que$supply\ function (q_s)\text{.}$ Si la cantidad baja demasiado el excedente del productor también bajará.

Ejemplo 7.8.3: Computación Pérdida de Ganancia Social.

Una tienda que intenta vender camisetas en el campus ha determinado que las funciones de oferta y demanda son:

\[ supply\ price(quantity)=5+\ln (quantity+10) \nonumber \]

\[ demand\ price(quantity)=10+100/(quantity+2) \nonumber \]

El dueño de la tienda tiene el monopolio en el campus y decide limitar la cantidad vendida a 200 playeras y cobrar lo que el mercado llevará. Encuentre el precio, el excedente del productor y los excedentes de consumo. Encuentra estos números si el propietario decide limitar las ventas a 50. ¿Cuántas playeras debe vender el dueño a qué precio para maximizar el excedente del productor? Si se maximiza el excedente del productor, ¿cuánto se reduce la ganancia social total?

Solución

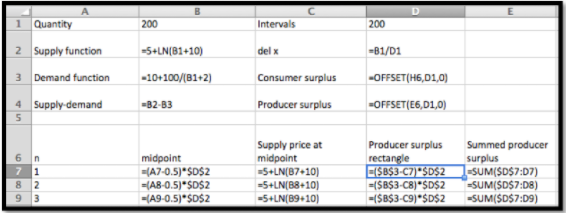
Las fórmulas involucradas para la oferta y la demanda son las mismas que usamos en el ejemplo 2. Con una ligera modificación si la hoja de trabajo de ese ejemplo podemos configurarla para calcular las sumas de Riemann aproximándose a los excedentes. En particular, utilizamos la función de demanda para encontrar la altura del excedente del productor. (Ver celda D7.)

$clipboard_e6a518a9aaba4c65c37a3b0e1f2768a06.png$

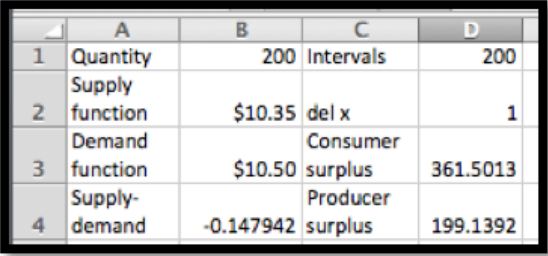
Si solo queremos vender 200 playeras, podemos subir el precio de $10.45 a $10.50. El excedente del productor sube de 191 dólares a 199 dólares. Sin embargo el superávit del consumidor cae de 372 dólares a 362 dólares.

$clipboard_e3e2cd98c91a74206c3e5e7b0265faab1.png$

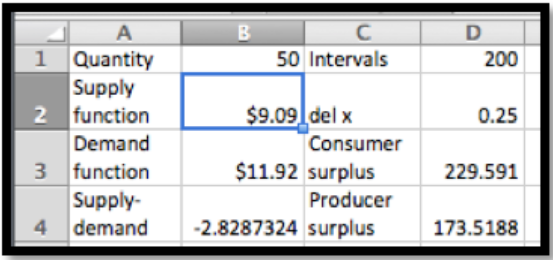
Si solo queremos vender 50 playeras, podemos subir el precio de $10.45 a $11.92. El excedente del productor cae de 191 dólares a 174 dólares. El excedente de consumo cae de 372 dólares a 230 dólares.

$clipboard_ec2a550bd0aacf097f39c5d88fdebef29.png$

Podemos usar solver para maximizar el excedente del Productor variando la cantidad. Una cantidad de 140 maximiza el excedente del productor en 210 dólares, pero está haciendo que la ganancia social total se haya reducido a 537 dólares desde 563 dólares.

$clipboard_e2d71314dfd399ea44d0a2c415daf18d6.png$

De igual manera, si los consumidores forman un cártel, pueden reducir artificialmente la demanda. Ya que entonces pagarán el precio de la oferta se disminuirá la ganancia social total, pero se podrá incrementar el excedente de los consumidores. En este caso el excedente del consumidor es la integral de la diferencia entre la función de demanda y el precio de oferta de la cantidad que se venderá.

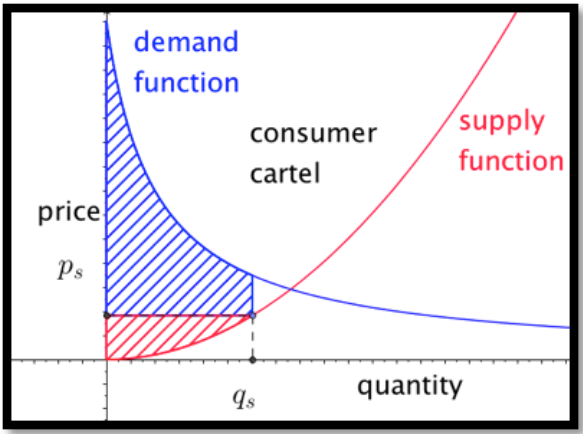
$clipboard_e8ca157e1888565ca1cdcad5efb995a22.png$

En el ejemplo que acabamos de ver, tanto las curvas de oferta como de demanda tienen una pequeña pendiente, por lo que el mercado es bastante elástico tanto desde el punto de vista de productores como de consumidores. En tal caso hay menos incentivo para formar un cártel. En otros mercados, como el gas y el petróleo, donde el mercado es más inelástico, hay más incentivo para dedicarse a prácticas monopolísticas.

Las curvas de Lorenz y el índice de Gini

Una pregunta que surge en la economía mira la equidad del ingreso o la distribución de la riqueza en un país. En las teorías económicas estándar, ya sea demasiada o muy poca equidad indica una falta de oportunidades y es un obstáculo para el crecimiento. No obstante, antes de poder abordar las ventajas o desventajas de un nivel de inequidad necesitamos poder cuantificar el nivel de equidad o inequidad. El método estándar es utilizar la curva de Lorenz y el índice de Gini.

La curva de Lorenz se define por una función$L(x)\text{,}$ con$0\le x\le 1\text{,}$ que mide la proporción de algo que se sostiene por la$x$ proporción inferior de la población. Así, si$L(0.2)=.1\text{,}$ para la función Lorenz por ingresos en un país, entonces el 20% inferior de la población gana el 10% de los ingresos del país. Dado que, bajo las definiciones habituales, una persona no puede tener ingresos negativos, las funciones de Lorenz son no negativas y van en aumento. Dado que las funciones de Lorenz se miden desde abajo, también tenemos$L(x)\le x$ para todos$x\text{.}$

Podemos hacer algunas observaciones más. La población en su conjunto tiene la totalidad de los ingresos de la población. Un conjunto vacío de la población no tiene ninguno de los ingresos de la población. Cualquier segmento inferior tendrá ingresos no negativos. En las fórmulas estas observaciones se convierten$L(1)=1\text{,}$$L(0)=0\text{,}$ y$L(x)\ge 0\text{,}$ para todos$x\text{,}$ respectivamente.

Si tuviéramos una equidad perfecta, nuestra función de Lorenz sería$L(x)=x\text{.}$ Cualquier curva de Lorenz que encontremos para una población real estará por debajo de esta curva. El índice de Gini (o coeficiente de Gini) mide el porcentaje que una curva real de Lorenz está por debajo de la curva ideal.

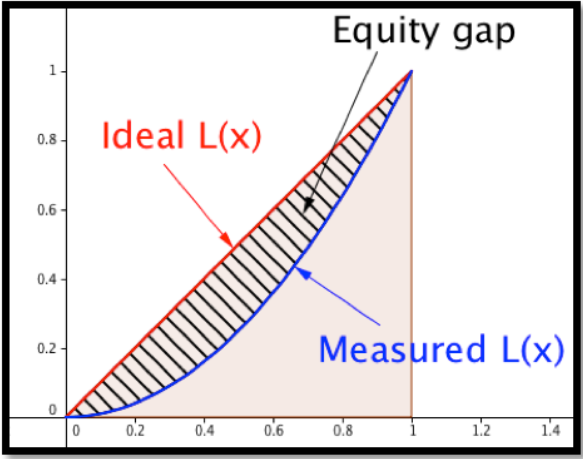
$clipboard_e4dcd5668bebe2b2ec8d2d2a7a708291c.png$

Computacionalmente,

\[ G=\frac{\int_0^1 (x-L(x))dx}{\int_0^1 x dx}=2\int_0^1 (x-L(x))dx. \nonumber \]

En la práctica este número suele multiplicarse por 100, reportando el porcentaje (0 a 100) en lugar de la proporción (0 a 1) del área bajo la función ideal y por encima de la función medida.

Ejemplo 7.8.4: Índice de Gini con una Fórmula para la Distribución del Ingreso.

La curva de Lorenz para el ingreso en un determinado país viene dada por$L(x)=.8x^3+.2x\text{.}$ ¿Qué proporción de los ingresos se obtiene por la mitad inferior de la población? Encuentra el índice de Gini.

Solución

Para encontrar la proporción ganada por la mitad inferior de la población sustituimos 0.5 en la ecuación.

\[ L(0.5)=(0.8) (0.5)^3+(0.2)(0.5)=0.1+0.1=0.2. \nonumber \]

Así, el 50% inferior de la población gana 20.% del ingreso total. Para calcular el índice de Gini, calculamos:

\[ G=2\int_0^1 (x-0.8x^3-0.2x)dx=(2)(0.4x^2-0.2x^4 ) |_0^1=.4 \nonumber \]

Por lo que el índice de Gini en este hipotético país es de 40. Para poner este número en contexto, el índice de Gini reportado para Estados Unidos en 2009 fue de 46.8.

En la práctica, el índice de Gini es una aplicación donde una aproximación numérica de una integral es el método más probable que se utilice. Es poco probable que obtengamos una fórmula para la distribución del ingreso. En cambio, es probable que encontremos puntos de datos. Dado que no existe un buen modelo de cómo se distribuirá el ingreso, simplemente podemos conectar los puntos con segmentos de línea y encontrar el área usando la fórmula de área para un trapecio.

Ejemplo 7.8.5: Índice de Gini con un Gráfico de Distribución del Ingreso.

Tenemos los siguientes datos de la oficina del censo sobre la distribución del ingreso en Estados Unidos en 2008. Calcular el índice de Gini.

Población% azulejo	0	20	40	60	80	90	100
Ingresos %azulejo	0	3.4	12.0	26.7	50.0	78.5	100

Solución

Recordamos que el área de un trapecio es (ancho) (altura promedio). Ponemos los datos en una hoja de cálculo.

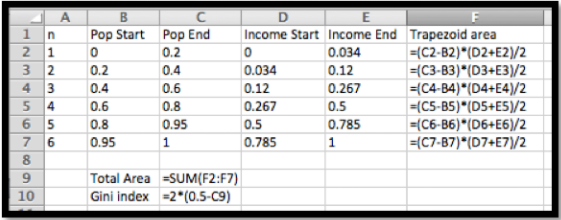
$clipboard_ef812fe258d2cb6784af846571777337e.png$

Después evaluamos las fórmulas.

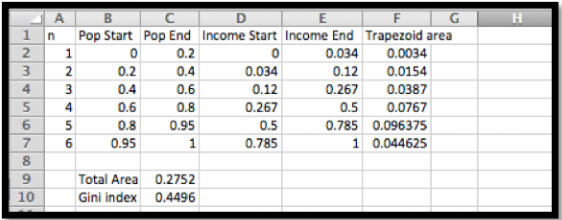
$clipboard_e595828261c7bf1b394756f8b94d7d2e9.png$

En porcentajes, el índice de Gini se aproxima a 45.

Ejercicios: Aplicaciones empresariales de los problemas integrales

clase=”

Para los ejercicios 1-6, supongamos que tenemos un mercado libre y que los bienes se venden en equilibrio de mercado. Encuentre el excedente del consumidor, el excedente del productor y la ganancia social total.

Ejercicio 1:

$SupplyPrice(q)= 50+q/2$y$DemandPrice(q)= 150-q/5\text{.}$

Responder: Las dos curvas se cruzan en el punto de equilibrio del mercado,$\left({\frac{1000}{7},\frac{850}{7}}\right)\text{.}$

\[ ProducerSurplus= \int_0^{1000/7} \left({\frac{850}{7}}\right)- \left({50+\frac{x}{2}}\right)\ dx=5102.04 \nonumber \]

\[ ConsumerSurplus= \int_0^{1000/7} \left({150-\frac{x}{5}}\right)-\left({\frac{850}{7}}\right)\ dx=2040.82. \nonumber \]

\[ TotalSocialGaine=ProducerSurplus+ConsumerSurplus=7142.86 \nonumber \]

Ejercicio 2:

$SupplyPrice(q)=\ln (q+10)$y$DemandPrice(q)= 100-q\text{.}$

Ejercicio 3:

$SupplyPrice(q)= 50(1-(0.99)^q)$y$DemandPrice(q)= 100(0.99)^q\text{.}$

Responder: Las dos curvas se cruzan en el punto de equilibrio del mercado,$(109.31, 33.33)\text{.}$

\[ ProducerSurplus= \int_0^{109.31} (33.33)- \left({50(1-(0.99)^q)}\right)\ dx=1494.79 \nonumber \]

\[ ConsumerSurplus= \int_0^{109.31} \left({100(0.99)^q}\right)-33.33)\ dx=2989.58. \nonumber \]

\[ TotalSocialGaine=ProducerSurplus+ConsumerSurplus=4484.37 \nonumber \]

Ejercicio 4:

$SupplyPrice(q)= 50(1-(0.95)^{q/10}$y$DemandPrice(q)= 150(0.95)^{q/10}\text{.}$

Ejercicio 5:

\[ SupplyPrice(q)=\begin{cases} 5&q\le 10\\ q^2/20&q>10\\ \end{cases} \nonumber \]

\[ DemandPrice(q)=\begin{cases} 100&q\le 10\\ 110-q&q>10\\ \end{cases} \nonumber \]

Responder

Las dos curvas se cruzan en el punto de equilibrio del mercado,$(37.958, 72.042)\text{.}$

\[ ProdSurplus= \int_0^{37.958} (72.042)- (SupplyPrice(q))\ dx=1789.732. \nonumber \]

El integral tiene que hacerse en dos partes con el descanso a las 10.

\[ ConsSurplus= \int_0^{37.958} DemandPrice(q)-72.042\ dx=670.405. \nonumber \]

\[ TotalSocialGain=ProdSurplus+ConsSurplus=2460.137. \nonumber \]

Ejercicio 6:

$SupplyPrice(q)= q/2$y

\[ DemandPrice(q)=\begin{cases} 200&q\le 10\\ 250*.8^{q/10}&q>10\\ \end{cases} \nonumber \]

Ejercicio 7:

Asumir OfertaPrecio (q) = 30+q y DemandPrice (q) = 170-q.

Encuentre el excedente del consumidor, el excedente del productor y la ganancia social total en el equilibrio del mercado.
Si los productores pueden formar un cártel y restringir la cantidad disponible a 50, vendiendo al precio de suministro por 50, ¿cuáles son el excedente del consumidor, el excedente del productor y la ganancia social total?
Encuentra el precio donde un cártel de productores maximizará el excedente del productor. Encuentra el excedente del productor a ese precio.

Responder

Las dos curvas se cruzan en el punto de equilibrio del mercado,$(70, 100)\text{.}$
\[ ProdSurplus= \int_0^{70} (100)- (30+q)\ dx=2450. \nonumber \]

\[ ConsSurplus= \int_0^{70} (170-q)-100\ dx=2450. \nonumber \]

\[ TotalSocialGain=ProdSurplus+ConsSurplus=4900. \nonumber \]