7.7: Aplicaciones de la Inversión Integral y Depreciación
- Page ID
- 115993
Habiendo mirado varias formas de evaluar integrales definidas, volvemos a problemas prácticos que podemos resolver siendo evaluando una integral. Dividiremos nuestras aplicaciones en esta sección en dos grupos. Los problemas en el primer grupo se reducen a la acumulación con el tiempo, y son análogos a encontrar el área bajo una curva, o encontrar una integral definida. Los problemas en el segundo grupo te piden encontrar un anti-derivado específico de una función. Se les llama problemas de valor límite.
Acumulación básica — El problema más directo para la integración es aquel en el que tengo una función para algún valor, como un flujo de ingresos, o materiales producidos, o un costo, y me interesa calcular cuánto se acumula en un intervalo especificado. Se trabaja a través de una serie de ejemplos donde la función de acumulación se complica progresivamente.
Mary dirige una pequeña tienda que está temporalmente desconectada de la red eléctrica. Un generador que proporciona energía utiliza 2 galones de combustible por hora. ¿Cuánto combustible necesita para mantener la tienda funcionando desde las 8 de la mañana hasta las 6 de la tarde?
Solución
Empezamos con un problema que es fácil de hacer sin cálculo para darnos confianza en nuestro método. Lo resolvemos primero con álgebra. Mary quiere hacer funcionar el generador por 10 horas y consume 2 galones de combustible por hora. Necesita (10 horas) (2 galones/hora) = 20 galones de combustible.
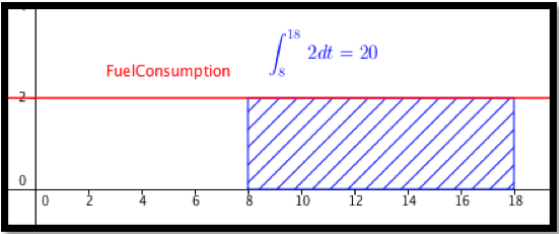
Para configurar el problema para el cálculo, usamos un reloj de 24 horas para poner tiempo en una línea numérica. Estamos acumulando\(FuelConsumption(t)=2\) de\(t=8\) a\(t=18\text{.}\) Necesitamos
\[ \int_8^{18} 2 dt=|2t|_8^{18}=(2*18)-(2*8)=20 \nonumber \]
galones de combustible.
\[ Marginal Cost(quantity)=50+quantity/1000 \nonumber \]
Encuentre el incremento en el costo a medida que la producción va de 50,000 a 80,000.
Solución
Dado que el cambio en el costo parece una suma de Riemann con 30,000 intervalos, aproximaremos el cambio de costo con la integral del costo marginal. Con esta función podemos encontrar fácilmente un antiderivado y evaluar. El cambio en el costo es
\[ \int_{50000}^{80000} 50+\frac{q}{1000} dq= \left.\left( 50q+\frac{q^2}{2000} \right)\right|_{50000}^{80000} \nonumber \]
\[ =(7,200,000)-(3,750,000)=3,450,000. \nonumber \]
El cambio en el costo de producción es de $3,450,000.


Un pozo petrolero en Texas produce inicialmente petróleo a una tasa de 2 millones de barriles de petróleo al año. La tasa de producción normalmente caerá 15% anual. ¿Cuánto petróleo se produce en un periodo de 5 años?
Solución
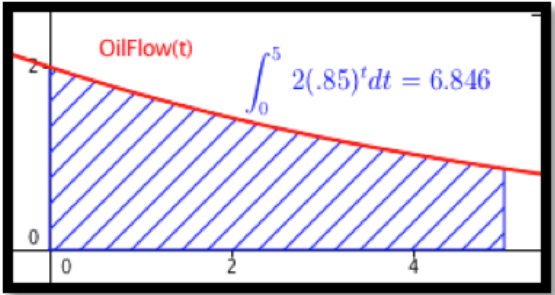
Queremos integrar nuestra tasa de producción de\(2(0.85)^t\) como\(t\) va de 0 a 5. Podemos utilizar nuestras fórmulas antidiferenciación para este problema.
\[ \int_0^5 2(0.85)^t dt= \left.\left(\frac{2(0.85)^t}{\ln (0.85)}\right)\right|_0^5=\frac{2}{\ln (0.85)} (0.85^5-1)=6.846. \nonumber \]
A lo largo de 5 años, el pozo producirá 6.846 millones de barriles de petróleo.

Su empresa está interesada en adquirir un flujo de ingresos que actualmente está produciendo son una tasa de 50+5 t mil dólares al año, donde t se mide en años. Para obtener el valor actual, se está descontando a una tasa de 6% /año compuesto continuamente. ¿Cuál es el valor actual de los primeros 10 años de ingresos del arroyo?
Solución
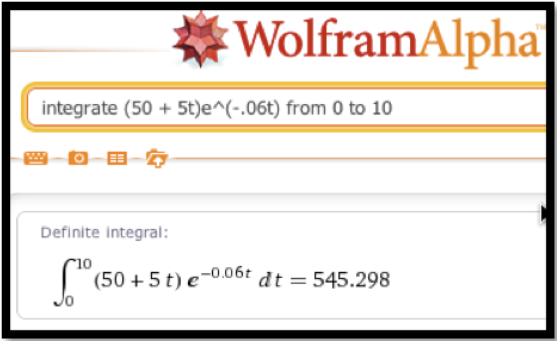
Para encontrar el ingreso total nos gustaría integrar\((50+5t)\) como\(t\) va de 0 a 10. Para encontrar el valor actual debemos descontar los ingresos con base en el momento en que lo recibamos. Así queremos integrar\((50+5t) e^{-0.06t}\) como\(t\) va de 0 a 10. Nosotros configuramos la integral\(\int_0^{10} (50+5t) e^{-0.06t} dt\text{.}\) Ya que no sabemos cómo encontrar el antiderivado para esta función, encontramos el área ya sea con sumas de Excel y Riemann, o con Wolfram Alpha.


Con cualquiera de los dos métodos, encontramos que el valor actual del flujo de ingresos es de $545,298.

Problemas de valor límite: Los problemas de acumulación le pidieron encontrar el área bajo una curva entre dos puntos específicos. Para esos problemas, no nos interesa una formulación de una función de área general. Un segundo conjunto de aplicaciones comienza con un derivado y está interesado en encontrar el anti-derivado particular que cumpla ciertas condiciones iniciales. (Utilizamos las condiciones para encontrar el valor correcto de “+C” en el anti-derivado general.) Estos problemas a menudo se resuelven una vez para encontrar el anti-derivado general para un tipo particular de problema, y la solución general se usa luego como fórmula para encontrar la constante C.
Pongo 20,000 dólares en una cuenta de retiro que gana 4% de intereses compuestos continuamente. Vuelvo a invertir todas mis ganancias de la cuenta en la cuenta de retiro. Quisiera una fórmula sencilla para el director en algún momento en el futuro.
Solución
Ya tenemos la fórmula para el crecimiento continuo, pero merece la pena derivarlo de nuevo. Se nos dice
\[ Principal' (time)=.05*Principal(time) \nonumber \]
o
\[ \frac{Principal' (time)}{Principal(time)}=.05 \nonumber \]
Integrando ambos lados con respecto al tiempo, obtenemos
\[ \ln (Principal(time))=.05*time+C \nonumber \]
Exponenciar ambos lados da
\[ Principal(time)=\exp(0.05*time)*\exp(C)=e^C e^{.05*time}. \nonumber \]
Ya que sabemos que el Principal es de 20,000 dólares en el momento 0, lo vemos\(e^C=20000\) y nuestra ecuación se simplifica a
\[ Principal(time)=20000e^{.05*time}. \nonumber \]
Esta es la fórmula que tomamos sobre la fe en el último capítulo.
Depreciación Al calcular los costos de una empresa, necesitamos evaluar el costo de depreciación de los equipos de capital. Hay una serie de formas razonables de calcular la depreciación.
- Depreciación en línea recta, que supone que una pieza de equipo pierde la misma cantidad de valor cada año hasta que no tiene valor.
\[ Annual\ Depreciation\ Expense= \frac{Cost\ of\ fixed\ Asset-Residual\ Value}{Useful\ life\ of\ Asset\ (in\ years)} \nonumber \]
- El método de la suma de dígitos de la depreciación. Se asume que la tasa de depreciación es proporcional a la vida útil restante esperada de la pieza de equipo. Por ejemplo, con un método de suma de años y definiendo V (t) como el valor, EL es la vida útil esperada, k es una constante, y t es tiempo, tendríamos:
\[ V' (t)= -k (EL-t) \nonumber \]
-
La depreciación del saldo decreciente. Este método asume que la tasa de depreciación es proporcional al valor actual, con la tasa inicial de depreciación dos veces la tasa lineal, con la depreciación detenida cuando el valor es el valor de chatarra. Dejamos que N sea la vida estimada del activo y dejamos que la tasa de depreciación sea:
\[ Depreciation\ rate=1- \sqrt[N]{ \frac{residual\ value}{cost\ of\ fixed\ asset}} \nonumber \]
Usted compra un auto por $18,000 y quiere depreciarlo a $0 en 5 años. Encuentra una fórmula para el valor del auto. Suponemos que el valor disminuye una tasa constante, por lo que utilizamos depreciación lineal. Dar una fórmula simple para encontrar el valor contable del equipo después de 3.5 años.
Solución
La forma más fácil de hacer este problema no es usar cálculo, sino darnos cuenta queremos la ecuación de una línea y tenemos dos puntos.
\[ Value(0)=18000 \hbox{ and } Value(5)=0. \nonumber \]
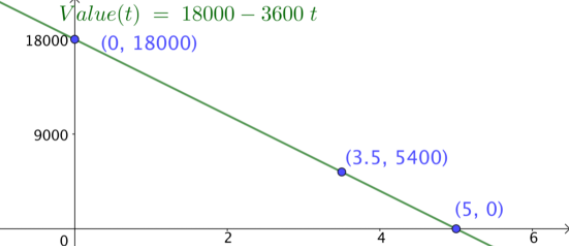
Tomando pendiente como subida sobre carrera, la pendiente es de -3,600 y la intercepción es de 18,000. Así nuestra ecuación es
\[ Value(time)=18000-3600*time. \nonumber \]
\[ Value(3.5)=5,400. \nonumber \]
Usando cálculo en el mismo problema que tenemos
\[ Value' (time)=-k\hbox{ for some constant }k, \nonumber \]
\[ Value(0)=18000\hbox{ and } Value(5)=0. \nonumber \]
.Integrar la primera ecuación da
\[ Value(time)=-k*time+C. \nonumber \]
Así, la depreciación en línea recta da una función de valor, que es una línea recta. Ahora conectamos valores conocidos para encontrar las constantes. Nos enchufamos\(time = 0\) para ver\(C = 18,000\text{.}\) Enchufamos\(time = 5\) para ver\(k = 3.600\text{.}\) Esto nos da la misma ecuación usando cálculo que obtuvimos usando álgebra. El valor contable del equipo a 3.5 años es de $5,400 con este método de depreciación.

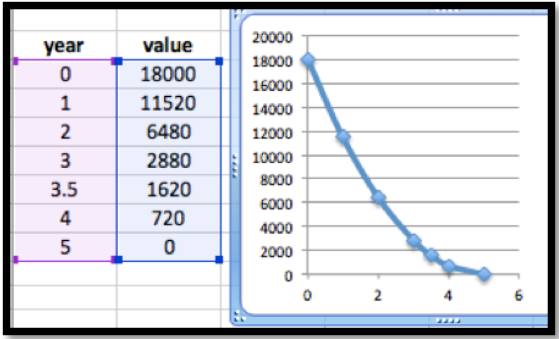
Después de comprar el mismo auto del ejemplo anterior, asumimos que la depreciación es proporcional a la cantidad de vida útil que le queda al equipo. (Un automóvil pierde más valor en su primer año que en su último año de vida). Producir una ecuación para el valor contable del mismo automóvil de $18,000 con este método.
Solución
Empezamos con la observación de que se nos da eso\(V' (t)=-k(EL-t)\) por alguna constante\(k\text{,}\) y lo sabemos\(V(0)=18,000\) y\(V(5)=0\text{.}\)
Con una vida útil esperada de 5, integrar la primera ecuación da
\[ Value(time)=-k*5*t+k*t^2/2+C. \nonumber \]
Así, el método de la suma de años da una función de valor que es cuadrática. Una vez más, conectamos puntos conocidos para encontrar las constantes. Conectamos por tiempo = 0 para ver C = 18,000. Conectamos por tiempo = 5 y obtenemos
\[ 0=-k*25+k*25/2+18,000. \nonumber \]
Resolviendo esto obtenemos\(k = 1,440\text{.}\) Nuestra fórmula de valor contable es entonces
\[ Value(time)=-7,200 t+720 t^2+18000. \nonumber \]
A 3.5 años el valor será
\[ Value(3.5)=-7,200*3.5+720*12.25+18000=1620. \nonumber \]
El valor contable a 3.5 años es de $1,620 con este método de depreciación.

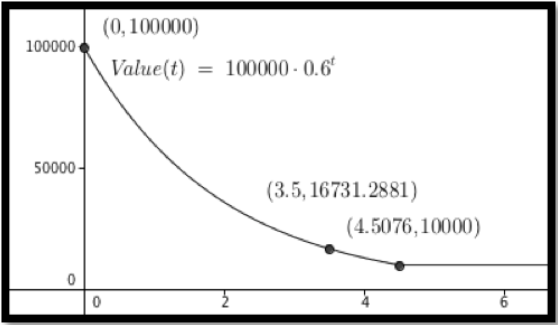
Este método de depreciación dice que un artículo pierde valor en proporción a su valor actual. El método estándar utiliza una tasa que es el doble de la tasa de depreciación lineal hasta que alcanzamos el valor de la chatarra, cuando la depreciación se detiene. Utilice este método para encontrar el valor contable de nuestro equipo de $100,000 a 3.5 años si el valor de la chatarra es de $10,000 y la vida útil es de 5 años.
Solución
En el ejemplo 5 vimos que el crecimiento proporcional o decaimiento dan una función exponencial. La función de valor básico es
\[ Value(time)=100000(1-2*.20)^{time}=100000(0.6)^{time}. \nonumber \]
Sin embargo, necesitamos encontrar cuándo la pieza de equipo deja de depreciarse. Resolviendo
\[ 10000=100000(0.6)^{time}. \nonumber \]
conseguimos
\[ .1=(0.6)^{time}. \nonumber \]
o
\[ time=\ln (0.1)/\ln (0.6) =4.508. \nonumber \]
Dado que 3.5 es menos de 4.5 años, el equipo sigue depreciándose. Su valor contable es\(100,000*(0.6)^{3.}5 = \$16,731\text{.}\)

Ejercicios: Aplicaciones de la integral: Problemas de inversión y depreciación
Los costos marginales para producir widgets es
\[ Marginal\ cost(q+1)=20-\frac{q}{10000} \nonumber \]
Encuentre el incremento en el costo al pasar de producir 60,000 unidades a producir 80,000 unidades.
- Contestar
-
\ begin {align*}\ hbox {costo aumentado}\ amp=\ int_ {start} ^ {stop}\ hbox {costo marginal}\ dq\\\ amp=\ int_ {60000} ^ {80000} (20-\ frac {q} {10000})\ dq\\ amp=\ izquierda. (20q-\ frac {q^2} {20000}\ |_ {60000} ^ {80000})\\\\ amp=1280000-1020000\\\ amp=260000\ final {alinear*}
El beneficio marginal para producir aparatitos es
\[ Marginal\ profit(q+1)=200-\frac{q}{1000}-\frac{q^2}{100,000,000} \nonumber \]
Encuentre el cambio en las ganancias al pasar de producir 70,000 unidades a producir 90,000 unidades.
Las proyecciones de ventas diarias para un artículo de moda son:
\[ Daily\ Sales(t)=100 t^2 e^{-t/5} \nonumber \]
Encuentra las ventas totales estimadas durante los primeros 100 días.
- Contestar
-


Esperamos ventas de unas 25000 unidades.
Las proyecciones diarias de ventas para un nuevo artículo son:
\[ Daily\ Sales(t)=100+10t-\frac{t^2}{100} \nonumber \]
Encuentra las ventas totales estimadas durante los primeros 200 días.
La producción de un pozo petrolero inicia a una tasa de 10,000 barriles anuales y disminuye exponencialmente a una tasa de 10% anual. ¿Cuánto se produce en 6 años?
- Contestar
-

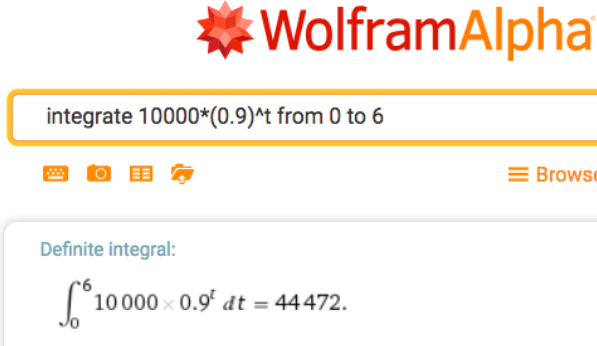
Esperamos 44,472 barriles de petróleo a lo largo de los 6 años.
Un pozo petrolero produce 15 mil barriles al año. La tasa de producción disminuye continuamente a una tasa de 10% anual. El pozo estará tapado como improductivo cuando produzca 3,000 barriles anuales. ¿Cuánto producirá antes de ser tapado?
Un flujo de ingresos produce a una tasa de 40,000 dólares anuales. Suponemos que la tasa de inversión libre de riesgo es de 3% anual. ¿Cuál es el valor actual del flujo de ingresos a lo largo de 20 años?
- Contestar
-

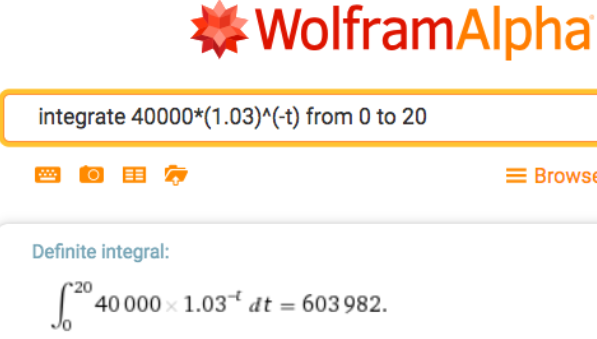
Evaluamos el valor de los ingresos por valor de 603,982 dólares.
Un flujo de ingresos produce a una tasa de\($40,000+$2,000t\) dólares por año con\(t\) medidas en años. Suponemos que la tasa de inversión libre de riesgo es de 3% anual. ¿Cuál es el valor actual del flujo de ingresos a lo largo de 20 años?

