7.4: Elegir una lista de prioridades
- Page ID
- 110812
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Exploraremos dos algoritmos para seleccionar una lista de prioridades.
Algoritmo de tiempo
El algoritmo de tiempo decreciente adopta el enfoque de tratar de sacar las tareas muy largas del camino lo antes posible colocándolas primero en la lista de prioridades.
Cree la lista de prioridades enumerando las tareas en orden desde el tiempo de finalización más largo hasta el tiempo de finalización más corto.
Considera el problema de programación representado por el dígrafo a continuación. Cree una lista de prioridades usando el algoritmo de lista de tiempo decreciente, luego úsela para programar dos procesadores usando el algoritmo de procesamiento de listas.
Solución
Para usar el algoritmo de lista de tiempo decreciente, creamos nuestra lista de prioridades enumerando las tareas en orden desde el tiempo de tarea más largo hasta el tiempo de tarea más corto. Si hay un empate, primero enumeraremos la tarea con un número de tarea más pequeño (no por ninguna buena razón, sino solo por consistencia).
Para este dígrafo, el algoritmo de tiempo decreciente crearía una lista de prioridades de:
\(\mathrm{T}_{6}(10), \mathrm{T}_{3}(7), \mathrm{T}_{10}(7), \mathrm{T}_{1}(6), \mathrm{T}_{5}(5), \mathrm{T}_{4}(4), \mathrm{T}_{7}(4), \mathrm{T}_{2}(3), \mathrm{T}_{8}(3), \mathrm{T}_{9}(2)\)
Una vez que tenemos la lista de prioridades, podemos crear el horario usando el algoritmo de procesamiento de listas. Con dos procesadores, obtendríamos:
Tiempo 0: Identificamos tareas listas, y asignamos\(\mathrm{T}_{3}\) a\(\mathrm{P}_{1}\) y\(\mathrm{T}_{1}\) a\(\mathrm{P}_{2}\)
Lista de prioridades:\(\mathrm{T}_{6}, \cancel{(\mathrm{T}_{3})}, \mathrm{T}_{10}, \cancel{(\mathrm{T}_{1})}, \mathrm{T}_{5}, (\mathrm{T}_{4}), \mathrm{T}_{7}, (\mathrm{T}_{2}), \mathrm{T}_{8}, \mathrm{T}_{9}\)

Tiempo 6:\(\mathrm{P}_{2}\) completa\(\mathrm{T}_{1}\). No se preparan nuevas tareas, por lo que\(\mathrm{T}_{4}\) se asigna a\(\mathrm{P}_{2}\).
Lista de prioridades:\(\mathrm{T}_{6}, \cancel{(\mathrm{T}_{3})}, \mathrm{T}_{10}, \xcancel{(\mathrm{T}_{1})}, \mathrm{T}_{5}, \cancel{(\mathrm{T}_{4})}, \mathrm{T}_{7}, (\mathrm{T}_{2}), \mathrm{T}_{8}, \mathrm{T}_{9}\)

Tiempo 7:\(\mathrm{P}_{1}\) completa\(\mathrm{T}_{3}\). No se preparan nuevas tareas, por lo que\(\mathrm{T}_{2}\) se asigna a\(\mathrm{P}_{1}\).
Lista de prioridades:\(\mathrm{T}_{6}, \xcancel{(\mathrm{T}_{3})}, \mathrm{T}_{10}, \xcancel{(\mathrm{T}_{1})}, \mathrm{T}_{5}, \cancel{(\mathrm{T}_{4})}, \mathrm{T}_{7}, \cancel{(\mathrm{T}_{2})}, \mathrm{T}_{8}, \mathrm{T}_{9}\)

Tiempo 10: Ambos procesadores completan sus tareas. \(\mathrm{T}_{6}\)se prepara, y se le asigna a\(\mathrm{P}_{1}\). No hay otras tareas listas, así que\(\mathrm{P}_{2}\) ociosas.
Lista de prioridades:\(\cancel{\mathrm{T}_{6}}, \xcancel{(\mathrm{T}_{3})}, \mathrm{T}_{10}, \xcancel{(\mathrm{T}_{1})}, \mathrm{T}_{5}, \xcancel{(\mathrm{T}_{4})}, \mathrm{T}_{7}, \xcancel{(\mathrm{T}_{2})}, \mathrm{T}_{8}, \mathrm{T}_{9}\)

Tiempo 20: Con\(\mathrm{T}_{6}\) completo,\(\mathrm{T}_{5}\) y\(\mathrm{T}_{7}\) estar listo, y se asignan a\(\mathrm{P}_{1}\) y\(\mathrm{P}_{2}\) respectivamente.
Lista de prioridades:\(\xcancel{(\mathrm{T}_{6})}, \xcancel{(\mathrm{T}_{3})}, \mathrm{T}_{10}, \xcancel{(\mathrm{T}_{1})}, \cancel{(\mathrm{T}_{5})}, \xcancel{(\mathrm{T}_{4})}, \cancel{(\mathrm{T}_{7})}, \xcancel{(\mathrm{T}_{2})}, \mathrm{T}_{8}, \mathrm{T}_{9}\)

Tiempo 24:\(\mathrm{P}_{2}\) completa\(\mathrm{T}_{7}\). No hay nuevos artículos listos, así que\(\mathrm{P}_{2}\) ociosos.
Tiempo 25:\(\mathrm{P}_{1}\) completa\(\mathrm{T}_{5}\). \(\mathrm{T}_{8}\)y\(\mathrm{T}_{9}\) se preparen, y se les asignen.
Lista de prioridades:\(\xcancel{(\mathrm{T}_{6})}, \xcancel{(\mathrm{T}_{3})}, \mathrm{T}_{10}, \xcancel{(\mathrm{T}_{1})}, \xcancel{(\mathrm{T}_{5})}, \xcancel{(\mathrm{T}_{4})}, \xcancel{(\mathrm{T}_{7})}, \xcancel{(\mathrm{T}_{2})}, \cancel{(\mathrm{T}_{8})}, \cancel{(\mathrm{T}_{9})}\)

Tiempo 27:\(\mathrm{T}_{9}\) se completa. No hay artículos listos, así que\(\mathrm{P}_{2}\) ociosos.
Tiempo 28:\(\mathrm{T}_{8}\) se completa. \(\mathrm{T}_{10}\)se prepara, y se le asigna a\(\mathrm{P}_{1}\).
Lista de prioridades:\(\xcancel{(\mathrm{T}_{6})}, \xcancel{(\mathrm{T}_{3})}, \cancel{(\mathrm{T}_{10})}, \xcancel{(\mathrm{T}_{1})}, \xcancel{(\mathrm{T}_{5})}, \xcancel{(\mathrm{T}_{4})}, \xcancel{(\mathrm{T}_{7})}, \xcancel{(\mathrm{T}_{2})}, \xcancel{(\mathrm{T}_{8})}, \xcancel{(\mathrm{T}_{9})}\)

Este es nuestro horario terminado, con un tiempo de finalización de 35.
Usando el algoritmo de tiempo decreciente, la lista de prioridades condujo a un horario con un tiempo de finalización de 35. ¿Esto es bueno? Ciertamente parece que hubo mucho tiempo de inactividad en este horario. Para tener una idea de lo bueno o malo que es este horario, podríamos calcular el tiempo crítico, el tiempo mínimo para completar el trabajo. Para encontrar esto, buscamos la secuencia de tareas con el mayor tiempo total de finalización. Para esta dígrafa esa secuencia parecería ser:\(\mathrm{T}_{2}, \mathrm{T}_{6}, \mathrm{T}_{5}, \mathrm{T}_{8}, \mathrm{T}_{10},\) con tiempo de secuencia total de 28. De esto podemos concluir que nuestro horario no es horrible, pero existe la posibilidad de que exista un mejor horario.
Determina la lista de prioridades para el dígrafo desde Pruébalo Ahora 1 usando el algoritmo de tiempo decreciente.
- Contestar
-
\(\mathrm{T}_{7}, \mathrm{T}_{1}, \mathrm{T}_{4,} \mathrm{T}_{2}, \mathrm{T}_{9}, \mathrm{T}_{5}, \mathrm{T}_{3}, \mathrm{T}_{6,} \mathrm{T}_{8}\)
Algoritmo de ruta
Una secuencia de tareas en el dígrafo se llama ruta. En el ejemplo anterior, vimos que el camino crítico dicta el tiempo mínimo de finalización para un horario. Quizás, entonces, tendría sentido considerar el camino crítico a la hora de crear nuestro horario. Por ejemplo, en el último horario, los procesadores comenzaron a trabajar en las tareas 1 y 3 porque eran tareas más largas, pero comenzar en la tarea 2 antes habría permitido que el trabajo comenzara en la tarea larga 6 antes.
El algoritmo de ruta crítica le permite crear una lista de prioridades basada en la idea de rutas críticas.
- Encuentra el camino crítico.
- La primera tarea en la ruta crítica se agrega a la lista de prioridades.
- Eliminar esa tarea del dígrafo
- Repetir, encontrar la nueva ruta crítica con el dígrafo revisado
El dígrafo original del Ejemplo 3 tiene ruta crítica\(\mathrm{T}_{2}, \mathrm{T}_{6}, \mathrm{T}_{5}, \mathrm{T}_{8}, \mathrm{T}_{10},\) por lo que\(\mathrm{T}_{2}\) se agrega primero a la lista de prioridades. Eliminando\(\mathrm{T}_{2}\) del dígrafo, ahora se ve así:
Solución
La ruta crítica (ruta más larga) en el dígrafo restante ahora es\(\mathrm{T}_{6}, \mathrm{T}_{5}, \mathrm{T}_{8}, \mathrm{T}_{10},\) así que\(\mathrm{T}_{6}\) se agrega a la lista de prioridades y se elimina.
Ahora hay dos caminos con la misma longitud más larga:\(\mathrm{T}_{1}, \mathrm{T}_{5}, \mathrm{T}_{8}, \mathrm{T}_{10}\) y\(\mathrm{T}_{3}, \mathrm{T}_{7}, \mathrm{T}_{8}, \mathrm{T}_{10}\). Podemos agregar\(\mathrm{T}_{1}\) a la lista de prioridades (o\(\mathrm{T}_{3}\) — usualmente agregamos la que tiene un número de artículo más pequeño) y eliminarla, y continuar con el proceso.
Estoy seguro de que puedes imaginar que buscar el camino crítico cada vez que eliminas una tarea del dígrafo se volvería realmente agotador, especialmente para un dígrafo grande. En la práctica, el algoritmo de ruta crítica se está implementando primero trabajando desde el final hacia atrás. Esto se llama el algoritmo de reflujo.
- Introducir un vértice “final” y asignarle un tiempo de 0, mostrado entre paréntesis
- Muévase hacia atrás a cada vértice que tenga una flecha al final y asígnele un tiempo crítico
- Desde cada uno de esos vértices, retroceda y asigna esos vértices a los tiempos críticos. Observe que el tiempo crítico para el vértice anterior será el tiempo de esa tarea más el tiempo crítico para el vértice posterior.
Ejemplo: Considera este segmento de dígrafo.
En este caso, si ya se ha determinado que T2 tiene un tiempo crítico de 10, entonces T1 tendrá un tiempo crítico de 5+10 = 15
Si ya ha asignado un tiempo crítico a un vértice, reemplázalo solo si el nuevo tiempo es mayor.
Ejemplo: En el dígrafo siguiente, T1 debe etiquetarse con un tiempo crítico de 16, ya que es el más largo de 5+10 y 5+11.
4. Repita hasta que todos los vértices estén etiquetados con sus tiempos críticos
Una vez que haya completado el algoritmo de reflujo, puede crear fácilmente la lista de prioridades de ruta crítica utilizando los tiempos críticos que acaba de encontrar.
- Aplicar el algoritmo de reflujo al dígrafo
- Cree la lista de prioridades enumerando las tareas en orden desde el tiempo crítico más largo hasta el tiempo crítico más corto
Esta versión del Algoritmo de Ruta Crítica suele ser la más fácil de implementar.
Aplicando esto a nuestro dígrafo del ejemplo anterior, comenzamos a aplicar el algoritmo de reflujo.
Solución
Agregamos un vértice final y le damos un tiempo crítico de 0.
Luego volvemos a\(\mathrm{T}_{4}, \mathrm{T}_{9},\) y\(\mathrm{T}_{10}\), etiquetándolos con sus tiempos críticos
De cada vértice marcado con un tiempo crítico, retrocedemos. \(\mathrm{T}_{7}\), por ejemplo, se etiquetará con un tiempo crítico 11 — el tiempo de tarea de 4 más el tiempo crítico de 7 para\(\mathrm{T}_{10}\). Porque\(\mathrm{T}_{5}\), hay dos caminos hasta el final. Utilizamos el más largo, etiquetando T 5 con tiempo crítico\(5+7 = 12\).
Continuar con el proceso hasta que se etiqueten todos los vértices. Observe que el tiempo crítico para el\(\mathrm{T}_{5}\) final fue reemplazado más tarde por el camino aún más largo a través\(\mathrm{T}_{8}\).
Ahora podemos crear rápidamente la lista de prioridades de ruta crítica enumerando las tareas en orden decreciente de tiempo crítico:
Lista de prioridades:\(\mathrm{T}_{2}, \mathrm{T}_{6}, \mathrm{T}_{1}, \mathrm{T}_{3}, \mathrm{T}_{5}, \mathrm{T}_{7}, \mathrm{T}_{8}, \mathrm{T}_{10}, \mathrm{T}_{4}, \mathrm{T}_{9}\)
Aplicando esta lista de prioridades usando el algoritmo de procesamiento de listas, obtenemos el horario:

En este caso particular, pudimos lograr el mínimo tiempo de finalización posible con este horario, sugiriendo que este horario es óptimo. Esto ciertamente no siempre es así.
Determine la lista de prioridades para el dígrafo desde Pruébalo Ahora 1 usando el algoritmo de ruta crítica.
- Contestar
-
Aplicando el algoritmo de reflujo, obtenemos esto:
La lista de prioridades de ruta crítica es:\(\mathrm{T}_{7}, \mathrm{T}_{1}, \mathrm{T}_{4}, \mathrm{T}_{2}, \mathrm{T}_{8}, \mathrm{T}_{5}, \mathrm{T}_{9}, \mathrm{T}_{3}, \mathrm{T}_{6}\)
Este ejemplo está diseñado para mostrar que el algoritmo de ruta crítica no siempre funciona maravillosamente. Programe las tareas en el dígrafo a continuación en tres procesadores usando el algoritmo de ruta crítica.
Solución
Para crear una lista de prioridades de ruta crítica, primero podríamos aplicar el algoritmo de reflujo:
Esto produce la lista de prioridades de ruta crítica:\(\mathrm{T}_{1}, \mathrm{T}_{6}, \mathrm{T}_{7}, \mathrm{T}_{8}, \mathrm{T}_{4}, \mathrm{T}_{5}, \mathrm{T}_{9}, \mathrm{T}_{2}, \mathrm{T}_{3}\).
La aplicación del algoritmo de procesamiento de listas a esta lista de prioridades conduce a la programación:
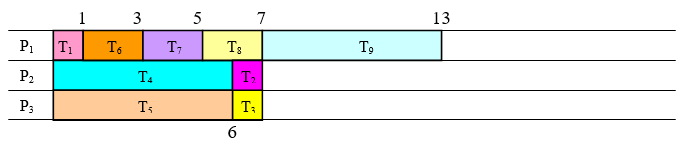
Este horario tiene tiempo de finalización de 13.
Por observación, podemos ver que existe un horario mucho mejor para el ejemplo anterior:

En la mayoría de los casos el algoritmo de ruta crítica conducirá a un muy buen horario. Hay casos, así, donde no lo hará. Desafortunadamente, no se conoce ningún algoritmo para producir siempre el horario óptimo.


