7.5: Ejercicios
- Page ID
- 110816
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Habilidades
- Cree un dígrafo para el siguiente conjunto de tareas:
\ (\ begin {array} {|l|l|l|}
\ hline\ text {Tarea} &\ text {Tiempo requerido} &\ begin {array} {l}
\ text {Tareas que deben ser}\\
\ text {completado primero}
\ end {array}\\ hline
\ mathrm {A} & 3 &\\\ hline\
\ hline\ mathrm {B } & 4 &\
\ hline\ mathrm {C} & 7 &\
\ hline\ mathrm {D} & 6 &\ mathrm {A},\ mathrm {B}\\
\ hline\ mathrm {E} & 5 &\ mathrm {B}\
\ hline\ mathrm {F} & 5 &\ mathrm {D},\ mathrm {E}\\
\ hline\ mathrm {G} & amp; 4 &\ mathrm {E}\\
\ hline
\ end {array}\)
- Cree un dígrafo para el siguiente conjunto de tareas:
\ (\ begin {array} {|l|l|l|}
\ hline\ text {Tarea} &\ text {Tiempo requerido} &\ begin {array} {l}
\ text {Tareas que deben ser}\\
\ text {completado primero}
\ end {array}\\ hline
\ mathrm {A} & 3 &\\\ hline\
\ hline\ mathrm {B } & 4 &\\ hline
\ mathrm {C} & 7 &\\\ hline\
mathrm {D} & 6 &\ mathrm {A}\\\ hline\ mathrm {E} & 5 &
\ mathrm {A}\\\ hline\ mathrm {F} & 5 &\ mathrm {B}\\
\ hline\ mathrm {G} & 4 &\ mathrm {B}\\ hline
\ mathrm {G} & 4 &\ mathrm {B}\\\ hline\ mathrm {rm {D},\ mathrm {E}\\
\ hline
\ end {array}\)
Usa este dígrafo para los siguientes 2 problemas.
- Usando la lista de prioridades\(\mathrm{T}_{4}, \mathrm{T}_{1}, \mathrm{T}_{7}, \mathrm{T}_{3}, \mathrm{T}_{6}, \mathrm{T}_{2}, \mathrm{T}_{5}\), programe el proyecto con dos procesadores.
- Usando la lista de prioridades\(\mathrm{T}_{5}, \mathrm{T}_{2}, \mathrm{T}_{3}, \mathrm{T}_{7}, \mathrm{T}_{1}, \mathrm{T}_{4}, \mathrm{T}_{6}\), programe el proyecto con dos procesadores.
Utilice este dígrafo para los siguientes 4 problemas.
- Usando la lista de prioridades,\(\mathrm{T}_{4}, \mathrm{T}_{3}, \mathrm{T}_{9}, \mathrm{T}_{10}, \mathrm{T}_{8}, \mathrm{T}_{5}, \mathrm{T}_{6}, \mathrm{T}_{1}, \mathrm{T}_{7}, \mathrm{T}_{2}\) programe el proyecto con dos procesadores.
- Usando la lista de prioridades,\(\mathrm{T}_{2}, \mathrm{T}_{4}, \mathrm{T}_{6}, \mathrm{T}_{8}, \mathrm{T}_{10}, \mathrm{T}_{1}, \mathrm{T}_{3}, \mathrm{T}_{5}, \mathrm{T}_{7}, \mathrm{T}_{9}\) programe el proyecto con dos procesadores.
- Usando la lista de prioridades,\(\mathrm{T}_{4}, \mathrm{T}_{3}, \mathrm{T}_{9}, \mathrm{T}_{10}, \mathrm{T}_{8}, \mathrm{T}_{5}, \mathrm{T}_{6}, \mathrm{T}_{1}, \mathrm{T}_{7}, \mathrm{T}_{2}\) programe el proyecto con tres procesadores.
- Usando la lista de prioridades,\(\mathrm{T}_{2}, \mathrm{T}_{4}, \mathrm{T}_{6}, \mathrm{T}_{8}, \mathrm{T}_{10}, \mathrm{T}_{1}, \mathrm{T}_{3}, \mathrm{T}_{5}, \mathrm{T}_{7}, \mathrm{T}_{9}\) programe el proyecto con tres procesadores.
- Utilice el algoritmo de tiempo decreciente para crear una lista de prioridades para el dígrafo a partir de #3, y programe con dos procesadores.
- Utilice el algoritmo de tiempo decreciente para crear una lista de prioridades para el dígrafo a partir de #3, y programe con tres procesadores.
- Utilice el algoritmo de tiempo decreciente para crear una lista de prioridades para el dígrafo a partir de #5, y programe con dos procesadores.
- Utilice el algoritmo de tiempo decreciente para crear una lista de prioridades para el dígrafo a partir de #5, y programe con tres procesadores.
- Utilice el algoritmo de tiempo decreciente para crear una lista de prioridades para el problema a partir de #1, y programe con dos procesadores.
- Utilice el algoritmo de tiempo decreciente para crear una lista de prioridades para el problema a partir de #2, y programe con dos procesadores.
- Con el dígrafo de #3:
a. Aplicar el algoritmo de reflujo para encontrar el tiempo crítico para cada tarea
b. Encontrar la ruta crítica para el proyecto y el tiempo mínimo de finalización
c. Utilice el algoritmo de ruta crítica para crear una lista de prioridades y una programación en dos procesadores.
- Con el dígrafo de #3, utilice el algoritmo de ruta crítica para programar en tres procesadores.
- Con el dígrafo de #5:
a. Aplicar el algoritmo de reflujo para encontrar el tiempo crítico para cada tarea
b. Encontrar la ruta crítica para el proyecto y el tiempo mínimo de finalización
c. Utilice el algoritmo de ruta crítica para crear una lista de prioridades y una programación en dos procesadores.
- Con el dígrafo de #5, utilice el algoritmo de ruta crítica para programar en tres procesadores.
- Utilice el algoritmo de ruta crítica para programar el problema desde #1 en dos procesadores.
- Utilice el algoritmo de ruta crítica para programar el problema desde #2 en dos procesadores.
Conceptos
- Si se agrega un requisito de pedido adicional a un dígrafo, ¿puede alargarse el tiempo óptimo de acabado? ¿Puede acortarse el tiempo óptimo de acabado?
- ¿Un horario óptimo no tendrá siempre tiempo de inactividad?
- Considera el dígrafo a continuación.
- ¿Cuántas listas de prioridades podrían crearse para estas tareas?
- ¿Cuántos horarios únicos crean esas listas de prioridades?
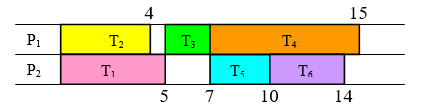
- Cree un dígrafo y una lista de prioridades que conduzcan al siguiente horario.
- ¿Es posible crear un dígrafo con tres tareas para las cuales cada lista de prioridades posible crea un horario diferente? Si es así, créelo.
- ¿Es posible crear un dígrafo con cuatro tareas para las cuales cada lista de prioridades posible crea un horario diferente? Si es así, créelo.
Exploración
- Las tareas independientes son aquellas que no tienen requisitos de pedido; se pueden completar en cualquier orden.
a. Considerar tres tareas, con tiempos de finalización 2, 2 y 4 horas respectivamente. Construya dos horarios diferentes en dos procesadores con diferentes tiempos de finalización para mostrar que la lista de prioridades sigue siendo importante con tareas independientes.
b. Elija un conjunto de tareas independientes con diferentes tiempos de finalización e implemente el algoritmo de lista de tiempos decrecientes y el algoritmo de ruta crítica. ¿Qué observas?
c. ¿El uso de la lista de tiempos decrecientes o algoritmos de ruta crítica con tareas independientes siempre producirá un horario óptimo? ¿Por qué o por qué no?
d. ¿El uso de la lista de tiempos decrecientes o algoritmos de ruta crítica con tareas independientes siempre producirá el mismo horario? ¿Por qué o por qué no?
- En grupo, elige diez tareas necesarias para hacer una fiesta de cumpleaños para un amigo o niño (por ejemplo, limpiar la casa o comprar un pastel). Determine los requisitos de orden para las tareas, cree un dígrafo y programe las tareas para dos personas.
29-37: Al final del capítulo se señaló que no existe ningún algoritmo para determinar si un horario arbitrario es óptimo, pero hay casos especiales donde podemos determinar que un horario es efectivamente óptimo. En cada uno de los siguientes escenarios, determine
- Si el escenario es incluso posible
- Si el horario podría ser óptimo o no
- Si podemos o no estar seguros de que el horario es óptimo
- Un trabajo tiene un tiempo crítico de 30 horas, y el tiempo de finalización para el horario en 2 procesadores es de 30 horas.
- La suma de todos los tiempos de tarea para un trabajo es de 40 horas, y el tiempo de finalización para el horario en 2 procesadores fue de 15 horas
- La suma de todos los tiempos de tarea para un trabajo es de 100 horas, el tiempo crítico del trabajo fue de 40 horas y el tiempo de finalización para el horario en 2 procesadores fue de 50 horas.
- La suma de todos los tiempos de tarea para un trabajo es de 50 horas, y el tiempo de finalización para el horario en 2 procesadores fue de 40 horas.
- Un trabajo tiene un tiempo crítico de 30 horas, y el tiempo de finalización para el horario en 3 procesadores es de 20 horas.
- La suma de todos los tiempos de tarea para un trabajo es de 60 horas, y el tiempo de finalización para el horario en 3 procesadores fue de 20 horas.
- El tiempo crítico para un trabajo es de 25 horas, y el tiempo de finalización para el horario en 2 procesadores fue de 30 horas.
- La suma de todos los tiempos de tarea para un trabajo es de 20 horas, y el tiempo de finalización para el horario en 2 procesadores fue de 25 horas.
- Con base en tus observaciones en los escenarios anteriores, escribe pautas para cuando puedas determinar que un horario es óptimo.