Saltar al contenido principal
LibreTexts Español

8.7: Ejercicios

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    110655

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Habilidades

    1. Actualmente Marko tiene 20 tulipanes en su patio. Cada año planta 5 más.
      1. Escribe una fórmula recursiva para el número de tulipanes que Marko tiene
      2. Escribe una fórmula explícita para el número de tulipanes que Marko tiene
    1. Pam es un Disc Jockey. Cada semana compra 3 nuevos álbumes para mantener actualizada su colección. Actualmente es dueña de 450 álbumes.
      1. Escribe una fórmula recursiva para el número de discos que Pam tiene
      2. Escribe una fórmula explícita para el número de discos que Pam tiene
    1. Las ventas de una tienda (en miles de dólares) crecen según la regla recursiva\(P_n=P_{n-1} + 15\), con población inicial\(P_0=40\).
      1. Calcular\(P_1\) y\(P_2\)
      2. Encuentra una fórmula explícita para\(P_n\)
      3. Usa tu fórmula para predecir las ventas de la tienda en 10 años
      4. ¿Cuándo superarán las ventas de la tienda los 100.000 dólares?
    1. El número de casas en un pueblo ha ido creciendo según la regla recursiva\(P_n=P_{n-1} + 30\), con población inicial\(P_0=200\).
      1. Calcular\(P_1\) y\(P_2\)
      2. Encuentra una fórmula explícita para\(P_n\)
      3. Usa tu fórmula para predecir el número de casas en 10 años
      4. ¿Cuándo llegará el número de casas a 400 casas?
    1. Una población de escarabajos está creciendo según un modelo de crecimiento lineal. La población inicial (semana 0) fue\(P_0=3\), y la población después de 8 semanas es\(P_8=67\).
      1. Encuentra una fórmula explícita para la población de escarabajos en la semana\(n\)
      2. ¿Después de cuántas semanas llegará la población de escarabajos a 187?
    1. El número de farolas en un pueblo está creciendo linealmente. Hace cuatro meses\((n = 0)\) había 130 luces. Ahora\((n = 4)\) hay 146 luces. Si esta tendencia continúa,
      1. Encuentra una fórmula explícita para el número de luces en el mes\(n\)
      2. ¿Cuántos meses tardarán en llegar a las 200 luces?
    1. La población de Tacoma en el año 2000 era de alrededor de 200 mil, y había ido creciendo alrededor de 9% cada año.
      1. Escribir una fórmula recursiva para la población de Tacoma
      2. Escribir una fórmula explícita para la población de Tacoma
      3. Si esta tendencia continúa, ¿cuál será la población de Tacoma en 2016?
      4. ¿Cuándo predice este modelo que la población de Tacoma supere los 400 mil?
    1. La población de Portland en 2007 era de aproximadamente 568 mil, y había estado creciendo alrededor de 1.1% cada año.
      1. Escribir una fórmula recursiva para la población de Portland
      2. Escribe una fórmula explícita para la población de Portland
      3. Si esta tendencia continúa, ¿cuál será la población de Portland en 2016?
      4. Si esta tendencia continúa, ¿cuándo llegará la población de Portland a 700 mil?
    1. Las enfermedades tienden a propagarse según el modelo de crecimiento exponencial. En los primeros días del SIDA, la tasa de crecimiento rondaba el 190%. En 1983, alrededor de 1700 personas en Estados Unidos murieron de SIDA. Si la tendencia hubiera continuado sin control, ¿cuántas personas habrían muerto de SIDA en 2005?
    1. La población del mundo en 1987 era de 5 mil millones y la tasa de crecimiento anual se estimó en 2 por ciento anual. Suponiendo que la población mundial siga un modelo de crecimiento exponencial, encuentre la población mundial proyectada en 2015.
    1. Se inicia un cultivo de bacterias con 300 bacterias. Después de 4 horas, la población ha crecido a 500 bacterias. Si la población crece exponencialmente,
      1. Escribir una fórmula recursiva para el número de bacterias
      2. Escribir una fórmula explícita para el número de bacterias
      3. Si esta tendencia continúa, ¿cuántas bacterias habrá en 1 día?
      4. ¿Cuánto tiempo tarda el cultivo en triplicar su tamaño?
    1. Una especie nativa de lobo ha sido reintroducida en un bosque nacional. Originalmente se trasplantaron 200 lobos. Después de 3 años, la población había crecido a 270 lobos. Si la población crece exponencialmente,
      1. Escribe una fórmula recursiva para el número de lobos
      2. Escribe una fórmula explícita para el número de lobos
      3. Si esta tendencia continúa, ¿cuántos lobos habrá en 10 años?
      4. Si esta tendencia continúa, ¿cuánto tiempo tardará la población en crecer a 1000 lobos?
    1. Cien truchas se siembran en un lago. Ausente restricción, su población crecerá 70% al año. El lago puede sostener un máximo de 2000 truchas. Utilizando el modelo de crecimiento logístico,
      1. Escribe una fórmula recursiva para el número de truchas
      2. Calcular el número de truchas después de 1 año y después de 2 años.
    1. Diez plantas de mora comenzaron a crecer en mi patio. Ausente restricción, las moras se esparcirán en 200% al mes. Mi patio sólo puede sostener unas 50 plantas. Utilizando el modelo de crecimiento logístico,
      1. Escribir una fórmula recursiva para el número de plantas de mora en mi patio
      2. Calcular el número de plantas después de 1, 2 y 3 meses
    1. En 1968, el salario mínimo de Estados Unidos era de $1.60 por hora. En 1976, el salario mínimo era de $2.30 por hora. Supongamos que el salario mínimo crece según un modelo exponencial donde n representa el tiempo en años posteriores a 1960.
      1. Encuentra una fórmula explícita para el salario mínimo.
      2. ¿Qué predice el modelo para el salario mínimo en 1960?
      3. Si el salario mínimo era de $5.15 en 1996, ¿es esto por encima, por debajo o igual a lo que predice el modelo?

    Conceptos

    1. La población de un pueblo pequeño puede ser descrita por la ecuación\(P_­n = 4000 + 70n\), donde\(n\) está el número de años después de 2005. Explique con palabras qué nos dice esta ecuación sobre cómo está cambiando la población.
    1. La población de un pueblo pequeño puede ser descrita por la ecuación\(P_­n = 4000(1.04)n\), donde\(n\) está el número de años después de 2005. Explique con palabras qué nos dice esta ecuación sobre cómo está cambiando la población.

    Exploración

    La mayoría de los ejemplos del texto examinaron cantidades crecientes, pero las ecuaciones lineales y exponenciales también pueden describir cantidades decrecientes, ya que los siguientes problemas explorarán.

    1. Un camión nuevo cuesta $32,000. El valor del automóvil se depreciará con el tiempo, lo que significa que perderá valor. Para efectos fiscales, la depreciación suele calcularse linealmente. Si el camión vale $24,500 después de tres años, escriba una fórmula explícita para el valor del automóvil después de\(n\) años.
    1. La inflación hace que las cosas cuesten más, y que nuestro dinero compre menos (de ahí que tus abuelos digan: “En mis días, podrías comprar una taza de café por una moneda de cinco mil dólares”). Supongamos que la inflación disminuye el valor del dinero en un 5% cada año. En otras palabras, si tienes $1 este año, el próximo año solo te comprará $0.95 en cosas. ¿Cuánto te comprarán $100 en 20 años?
    1. Supongamos que tienes un tazón de 500 caramelos M&M, y cada día comes\(\frac{1}{4}\) de los caramelos que tienes. ¿Cambia linealmente o exponencialmente el número de caramelos que quedan? Escribe una ecuación para modelar el número de caramelos que quedan después de n días.
    1. Un objeto cálido en una habitación más fría disminuirá de temperatura exponencialmente, acercándose a la temperatura ambiente de acuerdo con la fórmula donde Tn es la temperatura después de n minutos,\(r\) es la velocidad a la que cambia la temperatura, a es una constante, y Tr es la temperatura de la habitación. Los investigadores forenses pueden usar esto para predecir la hora de muerte de una víctima de homicidio. Supongamos que cuando se descubrió un cuerpo\((n = 0)\) era de 85 grados. Después de 20 minutos, la temperatura se midió nuevamente para ser de 80 grados. El cuerpo estaba en una habitación de 70 grados.
      1. Use la información dada con la fórmula proporcionada para encontrar una fórmula para la temperatura del cuerpo.
      2. ¿Cuándo murió la víctima, si el cuerpo comenzó a 98,6 grados?
    1. Las ecuaciones recursivas pueden ser muy útiles para modelar situaciones complicadas para las que las ecuaciones explícitas serían difíciles de interpretar. Como ejemplo, consideremos un lago en el que actualmente residen 2000 peces. La población de peces crece un 10% cada año, pero cada año 100 peces son cosechados del lago por personas que pescan.
      1. Escribir una ecuación recursiva para el número de peces en el lago después de n años.
      2. Calcular la población después de 1 y 2 años. ¿La población parece estar aumentando o disminuyendo?
      3. ¿Cuál es el número máximo de peces que se podrían cosechar cada año sin hacer que la población de peces disminuya a largo plazo?
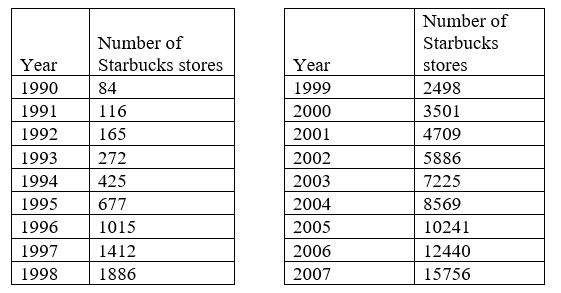
    1. El número de tiendas Starbucks creció después de que se abrieran por primera vez. A continuación se muestra el número de tiendas de 1990-2007, según lo informado en su página web corporativa [1].
      1. Trazar cuidadosamente los datos. ¿Se parece estar cambiando lineal o exponencialmente?
      2. Intente encontrar una ecuación para modelar los datos escogiendo dos puntos para trabajar. ¿Qué tan bien modela la ecuación los datos?
      3. Intente usar una ecuación de la forma, donde k es una constante, para modelar los datos. Este tipo de modelo se llama modelo Power. Compara tus resultados con los resultados de la parte\(b\). Nota: para utilizar este modelo, necesitará tener 1990 corresponder con\(n = 1\) en lugar de\(n = 0\).

    clipboard_e723972894bc819360fb5aa9fe3e212fd.png

    1. Thomas Malthus fue un economista que planteó el principio de que la población crece a partir de un modelo de crecimiento exponencial, mientras que los alimentos y los recursos crecen a partir de un modelo de crecimiento lineal. En base a esto, Malthus predijo que eventualmente la demanda de alimentos y recursos superaría a la oferta, con consecuencias de pesimismo y penumbra. Investiga un poco sobre Malthus para responder a estas preguntas.
      1. ¿Qué cambios sociales propuso Malthus para evitar el desenlace de la fatalidad que estaba prediciendo?
      2. ¿Por qué crees que sus predicciones no ocurrieron?
      3. ¿Cuáles son las similitudes y diferencias entre la teoría de Malthus y el modelo de crecimiento logístico?

    [1] www.Starbucks.com/aboutus/Company_Timeline.pdf recuperado en mayo de 2009

    This page titled 8.7: Ejercicios is shared under a CC BY-SA 3.0 license and was authored, remixed, and/or curated by David Lippman (The OpenTextBookStore) via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.