17.11: Formas de Argumentos Válidos

En lugar de hacer una tabla de verdad para cada argumento, es posible que podamos reconocer ciertas formas comunes de argumentos que son válidos (o inválidos). Si podemos determinar que un argumento se ajusta a una de las formas comunes, podemos declarar inmediatamente si es válido o no válido.

La Ley del Desapego (Modus Ponens)

La ley del desapego se aplica cuando un condicional y su antecedente se dan como premisas, y lo consecuente es la conclusión. La forma general es:

\(\begin{array} {ll} \text{Premise:} & p \rightarrow q \\ \text{Premise:} & p \\ \text{Conclusion:} & q \end{array}\)

El nombre latino, modus ponens, se traduce como “modo que afirma”.

Ejemplo 36

Recordemos este argumento de un ejemplo anterior:

\(\begin{array} {ll} \text{Premise:} & \text{If you bought bread, then you went to the store.} \\ \text{Premise:} & \text{You bought bread.} \\ \text{Conclusion:} & \text{You went to the store.} \end{array}\)

En forma simbólica:

\(\begin{array} {ll} \text{Premise:} & b \rightarrow s \\ \text{Premise:} & b \\ \text{Conclusion:} & s \end{array}\)

Este argumento tiene la estructura descrita por la ley del desapego. (La segunda premisa y la conclusión son simplemente las dos partes de la primera premisa desprendidas entre sí.) En lugar de hacer una tabla de la verdad, podemos decir que este argumento es válido al afirmar que satisface la ley del desapego.

La Ley de la Contraposición (Modus Tollens)

La ley de la contraposición se aplica cuando se dan como premisas un condicional y la negación de su consecuente, y la negación de su antecedente es la conclusión. La forma general es:

\(\begin{array} {ll} \text{Premise:} & p \rightarrow q \\ \text{Premise:} & \sim q \\ \text{Conclusion:} & \sim p \end{array}\)

El nombre latino, modus tollens, se traduce como “modo que niega”.

Observe que la segunda premisa y la conclusión parecen la contrapositiva de la primera premisa\(\sim q \rightarrow \sim p\), pero se han desapegado. Se puede pensar en la ley de la contraposición como una combinación de la ley del desapego y el hecho de que lo contrapositivo es lógicamente equivalente al enunciado original.

Ejemplo 37

\(\begin{array} {ll} \text{Premise:} & \text{If I drop my phone into the swimming pool, my phone will be ruined.} \\ \text{Premise:} & \text{My phone isn’t ruined.} \\ \text{Conclusion:} & \text{I didn’t drop my phone into the swimming pool.} \end{array}\)

Si dejamos\(d=\mathrm{I}\) caer el teléfono en la piscina y\(r=\) el teléfono se arruina, entonces podemos representar el argumento de esta manera:

\(\begin{array} {ll} \text{Premise:} & d \rightarrow r \\ \text{Premise:} & \sim r \\ \text{Conclusion:} & \sim d \end{array}\)

La forma de este argumento coincide con lo que necesitamos para invocar la ley de la contraposición, por lo que es un argumento válido.

Pruébalo ahora 14

¿Es válido este argumento?

\(\begin{array} {ll} \text{Premise:} & \text{If you brushed your teeth before bed, then your toothbrush will be wet.} \\ \text{Premise:} & \text{Your toothbrush is dry.} \\ \text{Conclusion:} & \text{You didn’t brush your teeth before bed.} \end{array}\)

Responder

Deje\(b=\) cepillarse los dientes y el\(w=\) cepillo de dientes esté mojado

\(\begin{array} {ll} \text{Premise:} & b \rightarrow w \\ \text{Premise:} & \sim w \\ \text{Conclusion:} & \sim b \end{array}\)

Este argumento es válido por la Ley de Contraposición.

La propiedad transitiva (silogismo hipotético)

El inmueble transitivo tiene como premisas una serie de condicionales, donde el consecuente de uno es el antecedente del siguiente. La conclusión es un condicional con el mismo antecedente que la primera premisa y el mismo consecuente que la premisa final. La forma general es:

\(\begin{array} {ll} \text{Premise:} & p \rightarrow q \\ \text{Premise:} & q \rightarrow r \\ \text{Conclusion:} & p \rightarrow r \end{array}\)

El ejemplo anterior sobre la compra de una camisa en el centro comercial es un ejemplo que ilustra la propiedad transitiva. Describe una reacción en cadena: si sucede lo primero, entonces sucede lo segundo, y si sucede lo segundo, entonces sucede lo tercero. Por lo tanto, si queremos ignorar lo segundo, podemos decir que si sucede lo primero, entonces sabemos que va a pasar lo tercero. No tenemos que mencionar la parte de comprar jeans; simplemente podemos decir que el primer evento lleva al evento final. Incluso podríamos tener más de dos premisas; siempre y cuando formen una reacción en cadena, la propiedad transitiva nos dará un argumento válido.

Ejemplo 38

\(\begin{array} {ll} \text{Premise:} & \text{If a soccer player commits a reckless foul, she will receive a yellow card.} \\ \text{Premise:} & \text{If Hayley receives a yellow card, she will be suspended for the next match.} \\ \text{Conclusion:} & \text{If Hayley commits a reckless foul, she will be suspended for the next match.} \end{array}\)

Si dejamos\(r=\) cometer una falta imprudente,\(y=\) recibir una tarjeta amarilla y\(s=\) ser suspendidos, entonces nuestro argumento se ve así:

\(\begin{array} {ll} \text{Premise:} & r \rightarrow y \\ \text{Premise:} & y \rightarrow s \\ \text{Conclusion:} & r \rightarrow s \end{array}\)

Este argumento tiene la estructura exacta requerida para usar la propiedad transitiva, por lo que es un argumento válido.

Pruébalo ahora 15

¿Es válido este argumento?

\(\begin{array} {ll} \text{Premise:} & \text{If the old lady swallows a fly, she will swallow a spider.} \\ \text{Premise:} & \text{If the old lady swallows a spider, she will swallow a bird.} \\ \text{Premise:} & \text{If you brushed your teeth before bed, then your toothbrush will be wet.} \\ \text{Premise:} & \text{If you brushed your teeth before bed, then your toothbrush will be wet.} \\\text{Premise:} & \text{If the old lady swallows a bird, she will swallow a cat.} \\ \text{Premise:} & \text{If the old lady swallows a cat, she will swallow a dog.} \\\text{Premise:} & \text{If the old lady swallows a dog, she will swallow a goat.} \\ \text{Premise:} & \text{If the old lady swallows a goat, she will swallow a cow.} \\ \text{Premise:} & \text{If the old lady swallows a cow, she will swallow a horse.} \\ \text{Premise:} & \text{If the old lady swallows a horse, she will die, of course.} \\ \text{Conclusion:} & \text{If the old lady swallows a fly, she will die, of course.} \end{array}\)

Responder

Este argumento es válido por la Propiedad Transitiva, que puede involucrar a más de dos premisas, siempre y cuando continúen la reacción en cadena. El local se\(f \rightarrow s, s \rightarrow b, b \rightarrow c, c \rightarrow d\)\(d \rightarrow g, g \rightarrow w, w \rightarrow h, h \rightarrow x\) puede reducir a\(f \rightarrow x. \) (Porque ya habíamos usado\(c\) y\(d\) decidimos usar\(w\) para vaca y\(x\) para la muerte. Si la anciana se traga la mosca, eventualmente se comerá un caballo y morirá.

Silogismo Disyuntivo

En un silogismo disyuntivo, las premisas consisten en una o declaración y la negación de una de las opciones. La conclusión es la otra opción. La forma general es:

\(\begin{array} {ll} \text{Premise:} & p \vee q \\ \text{Premise:} & \sim p \\ \text{Conclusion:} & q \end{array}\)

El orden de las dos partes de la disyunción no es importante. En otras palabras, podríamos tener las premisas\(p \vee q\) y\(\sim q,\) y la conclusión\(p\)

Ejemplo 39

\(\begin{array} {ll} \text{Premise:} & \text{I can either drive or take the train.} \\ \text{Premise:} & \text{I refuse to drive.} \\ \text{Conclusion:} & \text{I will take the train.} \end{array}\)

Si dejamos\(d=I\) conducir y\(t=I\) tomar el tren, entonces la representación simbólica del argumento es:

\(\begin{array} {ll} \text{Premise:} & d \vee t \\ \text{Premise:} & \sim d \\ \text{Conclusion:} & t \end{array}\)

Este argumento es válido porque tiene la forma de un silogismo disyuntivo. Tengo dos opciones, y una de ellas no va a pasar, entonces la otra debe suceder.

Pruébalo ahora 16

¿Es válido este argumento?

\(\begin{array} {ll} \text{Premise:} & \text{Alison was required to write a 10-page paper or give a 5-minute speech.} \\ \text{Premise:} & \text{Alison did not give a 5-minute speech.} \\ \text{Conclusion:} & \text{Alison wrote a 10-page paper.} \end{array}\)

Responder

Let\(p=\) escribió una ponencia y\(s=\) dio un discurso.

\(\begin{array} {ll} \text{Premise:} & p \vee s \\ \text{Premise:} & -s \\ \text{Conclusion:} & p \end{array}\)

Este argumento es válido por el silogismo disyuntivo. Alison tuvo que hacer uno u otro; ella no eligió el discurso, así que debió haber elegido el papel.

Ten en cuenta que, cuando estés determinando la validez de un argumento, debes asumir que las premisas son verdaderas. Si no estás de acuerdo con alguna de las premisas, necesitas mantener tu opinión personal fuera de ella. Tu trabajo es fingir que las premisas son verdaderas y luego determinar si te obligan a aceptar la conclusión. Se puede atacar las premisas en un tribunal de justicia o en una discusión política, claro, pero aquí nos estamos enfocando en la estructura de los argumentos, no en la verdad de lo que realmente dicen.

Acabamos de mirar cuatro formas de argumentos válidos; hay dos formas comunes que representan argumentos inválidos, a los que también se les llama falacias.

La falacia de lo Converso

La falacia de lo contrario surge cuando un condicional y su consecuente se dan como premisas, y el antecedente es la conclusión. La forma general es:

\(\begin{array} {ll} \text{Premise:} & p \rightarrow q \\ \text{Premise:} & q \\ \text{Conclusion:} & p \end{array}\)

Observe que la segunda premisa y la conclusión parecen lo contrario de la primera premisa\(q \rightarrow p\), pero se han desapegado. La falacia de lo contrario intenta incorrectamente afirmar que lo contrario de una declaración es equivalente a esa afirmación.

Ejemplo 40

\(\begin{array} {ll} \text{Premise:} & \text{If I drink coffee after noon, then I have a hard time falling asleep that night.} \\ \text{Premise:} & \text{I had a hard time falling asleep last night.} \\ \text{Conclusion:} & \text{I drank coffee after noon yesterday.} \end{array}\)

Si dejamos\(c=\mathrm{I}\) tomar café después del mediodía y\(h=\mathrm{I}\) nos cuesta conciliar el sueño, entonces nuestro argumento se ve así:

\(\begin{array} {ll} \text{Premise:} & c \rightarrow h \\ \text{Premise:} & h \\ \text{Conclusion:} & c \end{array}\)

Este argumento utiliza el razonamiento inverso, por lo que es un argumento inválido. Podría haber muchas otras razones por las que no podía quedarme dormido: podría estar preocupado por el dinero, mis vecinos podrían haber estado encendiendo fuegos artificiales,...

Pruébalo ahora 17

¿Es válido este argumento?

\(\begin{array} {ll} \text{Premise:} & \text{If you pull that fire alarm, you will get in big trouble.} \\ \text{Premise:} & \text{You got in big trouble.} \\ \text{Conclusion:} & \text{You must have pulled the fire alarm.} \end{array}\)

Responder

\(f=\)Dejé tirado alarma de incendio y\(t=\) se metió en grandes problemas.

\(\begin{array} {ll} \text{Premise:} & f \rightarrow t \\ \text{Premise:} & t \\ \text{Conclusion:} & f \end{array}\)

La falacia de lo inverso

La falacia de lo inverso ocurre cuando un condicional y la negación de su antecedente se dan como premisas, y la negación de lo consecuente es la conclusión. La forma general es:

\(\begin{array} {ll} \text{Premise:} & p \rightarrow q \\ \text{Premise:} & \sim p \\ \text{Conclusion:} & \sim q \end{array}\)

Nuevamente, fíjense que la segunda premisa y la conclusión parecen la inversa de la primera premisa\(\sim p \rightarrow \sim q\), pero se han desapegado. La falacia de la inversa intenta incorrectamente afirmar que la inversa de una declaración es equivalente a esa declaración.

Ejemplo 41

\(\begin{array} {ll} \text{Premise:} & \text{If you listen to the Grateful Dead, then you are a hippie.} \\ \text{Premise:} & \text{Sky doesn’t listen to the Grateful Dead.} \\ \text{Conclusion:} & \text{Sky is not a hippie.} \end{array}\)

Si dejamos\(g=\) escuchar a The Grateful Dead y\(h=\) es hippie, entonces este es el argumento:

\(\begin{array} {ll} \text{Premise:} & g \rightarrow h \\ \text{Premise:} & \sim g \\ \text{Conclusion:} & \sim h \end{array}\)

Este argumento no es válido porque utiliza razonamiento inverso. La primera premisa no implica que todos los hippies escuchen a los Grateful Dead; podría haber algunos hippies que escuchen Phish en su lugar.

Pruébalo ahora 18

¿Es válido este argumento?

\(\begin{array} {ll} \text{Premise:} & \text{If a hockey player trips an opponent, he will be assessed a 2-minute penalty.} \\ \text{Premise:} & \text{Alexei did not trip an opponent.} \\ \text{Conclusion:} & \text{Alexei will not be assessed a 2-minute penalty.} \end{array}\)

Responder

Vamos\(t=\) tropezó y\(p=\) consiguió un penalti.

\(\begin{array} {ll} \text{Premise:} & t \rightarrow p \\ \text{Premise:} & \sim t \\ \text{Conclusion:} & \sim p \end{array}\)

Este argumento no es válido porque tiene la forma de la Falacia de la Inversa. Alexei pudo haber recibido una sanción por una infracción que no sea tropezar.

Por supuesto, los argumentos no se limitan a estas seis formas básicas; algunos argumentos tienen más premisas, o premisas que necesitan ser reordenadas antes de que se pueda ver lo que realmente está sucediendo. Hay muchas otras formas de argumentos que no son válidos. Sin embargo, si un argumento no parece ajustarse al patrón de ninguna de estas formas comunes, es posible que desee usar un diagrama de Venn o una tabla de verdad en su lugar.

Lewis Carroll, autor de Las aventuras de Alicia en el país de las maravillas, fue profesor de matemáticas y lógica, y escribió dos libros sobre lógica. En ellas, propondría premisas como rompecabezas, para ser conectadas mediante silogismos. El siguiente ejemplo es uno de esos acertijos.

Ejemplo 42

Resuelve el rompecabezas. Es decir, encontrar una conclusión lógica a partir de estas premisas.

Todos los bebés son ilógicos.

No se desprecia a nadie que pueda manejar a un cocodrilo.

Las personas ilógicas son despreciadas.

Dejar\(b=\) es un bebé,\(d=\) es despreciado,\(i=\) es ilógico, y\(m=\) puede manejar a un cocodrilo.

Entonces podemos escribir las premisas como:

\(b \rightarrow i\)

\(m \rightarrow \sim d\)

\(i \rightarrow d\)

Escribir correctamente la segunda premisa puede ser un desafío; puede reformularse como “Si puedes manejar a un cocodrilo, entonces no te desprecian”.

Utilizando la propiedad transitiva con la primera y tercera premisas, podemos concluir que\(b \rightarrow d\), que todos los bebés son despreciados. Usando el contrapositivo de la segunda premisa,\(d \rightarrow \sim m\), entonces podemos usar la propiedad transitiva con\(b \rightarrow d\) para concluir que\(b \rightarrow \sim m\), que los bebés no pueden manejar cocodrilos. Si bien es una tontería, esta es una conclusión lógica desde las premisas dadas.

Ejemplo 43

\(\begin{array} {ll} \text{Premise:} & \text{If I work hard, I’ll get a raise.} \\ \text{Premise:} & \text{If I get a raise, I’ll buy a boat.} \\ \text{Conclusion:} & \text{If I don’t buy a boat, I must not have worked hard.} \end{array}\)

Si dejamos\(h=\) trabajar duro,\(r=\) conseguir un aumento y\(b=\) comprar un barco, entonces podemos representar simbólicamente nuestro argumento:

\(\begin{array} {ll} \text{Premise:} & h \rightarrow r \\ \text{Premise:} & r \rightarrow b \\ \text{Conclusion:} & \sim b \rightarrow \sim h \end{array}\)

Usando la propiedad transitiva con las dos premisas, podemos concluir que\(h \rightarrow b\), si trabajo duro, entonces compraré una embarcación. Cuando nos enteramos de lo contrapositivo, vimos que la declaración condicional\(h \rightarrow b\) es equivalente a\(\sim b \rightarrow \sim h\). Por lo tanto, la conclusión es efectivamente un silogismo lógico derivado de las premisas.

Pruébalo ahora 19

¿Es válido este argumento?

\(\begin{array} {ll} \text{Premise:} & \text{If I go to the party, I’ll be really tired tomorrow.} \\ \text{Premise:} & \text{If I go to the party, I’ll get to see friends.} \\ \text{Conclusion:} & \text{If I don’t see friends, I won’t be tired tomorrow.} \end{array}\)

Responder

\(p=\)Déjate ir a la fiesta,\(t=\) cansarte y\(f=\) ver amigos.

\(\begin{array} {ll} \text{Premise:} & p \rightarrow t \\ \text{Premise:} & p \rightarrow f \\ \text{Conclusion:} & -f \rightarrow \sim t \end{array}\)

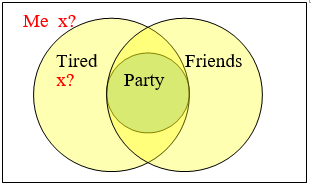Podríamos intentar reescribir la segunda premisa usando lo contrapositivo a estado\(\sim f \rightarrow \sim p\), pero eso no nos permite formar un silogismo. Si no veo amigos, entonces no fui a la fiesta, pero eso no es suficiente para afirmar que no voy a estar cansado mañana. A lo mejor me quedé despierta toda la noche viendo películas.

Un diagrama de Venn puede ayudar, si lo configuramos correctamente. El círculo “partidista” debe estar completamente contenido dentro de la intersección de los otros círculos. Sabemos que estoy en algún lugar fuera del círculo de “amigos”, pero no podemos determinar si estoy en el círculo “cansado”. Todo lo que realmente sabemos con certeza es que no fui a la fiesta.