8.1: Principal, Tarifa, Tiempo
- Page ID
- 110767
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Sus inversiones pueden estar en riesgo si los mercados de acciones y bonos se desploman, como predice una historia en Globe and Mail. Te preguntas si deberías cambiar tu dinero en inversiones a corto plazo relativamente seguras hasta que el mercado vuelva a explotar. Considera su cuenta de ahorros de alto interés, pero se da cuenta de que solo los primeros $60,000 de su cuenta de ahorros están asegurados. Quizás deberías poner algo de ese dinero en letras del tesoro en su lugar.
De cara al futuro, ¿de qué ingresos vivirás una vez que ya no estés trabajando? A medida que tu carrera se desarrolla, necesitas ahorrar dinero para financiar tu estilo de vida en la jubilación. Algún día tendrás $100,000 o más que debes invertir y reinvertir para alcanzar tus metas financieras de jubilación.
Para tomar tales decisiones, primero se debe entender cómo calcular el interés simple. En segundo lugar, es necesario comprender las características de las diversas opciones financieras que utilizan interés simple. Armado con este conocimiento, ¡puedes tomar decisiones financieras inteligentes!
El mundo de las finanzas calcula los intereses de dos maneras diferentes:
- Interés Simple. Un sistema de interés simple se aplica principalmente a las transacciones financieras a corto plazo, con un marco de tiempo inferior a un año. En este sistema, que se explora en este capítulo, los intereses devengan pero no se componen.
- Interés Compuesto. Un sistema de interés compuesto se aplica principalmente a las transacciones financieras a largo plazo, con un marco de tiempo de un año o más. En este sistema, que explora el siguiente capítulo, los intereses se devengan y se agravan sobre los intereses devengados anteriormente.
Interés Sencillo
En un entorno de interés simple, calculas los intereses únicamente sobre la cantidad de dinero al inicio de la transacción. Cuando finaliza el plazo de la transacción, se agrega el monto del interés simple al monto inicial. Por lo tanto, a lo largo de toda la transacción la cantidad de dinero colocada en la cuenta permanece sin cambios hasta que expire el plazo. Es sólo en esta fecha cuando aumenta la cantidad de dinero. Así, un inversionista tiene más dinero o un prestatario debe más dinero al final.
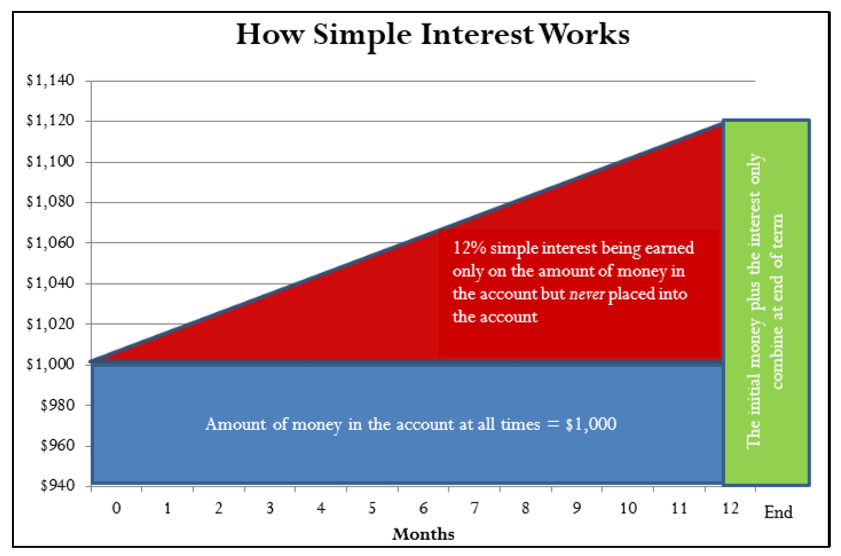
La figura ilustra el concepto de interés simple. En este ejemplo, supongamos que $1,000 se coloca en una cuenta con 12% de interés simple por un periodo de 12 meses. Durante todo el plazo de esta transacción, la cantidad de dinero en la cuenta siempre es igual a $1,000. Durante este periodo, los intereses se devengan a una tasa del 12%, pero el interés nunca se coloca en la cuenta. Cuando la transacción termina después de 12 meses, los $120 de interés y los $1,000 iniciales se combinan para sumar $1,120.
Un préstamo o inversión siempre implica dos partes, una dando y otra recibiendo. No importa en qué parte se encuentre en la transacción, el monto de los intereses permanece sin cambios. La única diferencia radica en si estás ganando o pagando los intereses.
- Si consigues un préstamo personal de un banco, el banco te da el dinero y tú recibes el dinero. En esta situación, el banco gana el interés simple y te están cobrando intereses simples sobre tu préstamo. En la cifra, esto significa que debes devolver no solo los $1,000 que tomaste prestado inicialmente sino $120 adicionales en intereses.
- Si colocas tu dinero en una cuenta de inversión del banco, has dado el dinero y el banco ha recibido el dinero. En esta situación, ganas el simple interés de tu dinero y el banco paga intereses simples a tu cuenta de inversión. En la figura, esto significa que el banco debe devolverte tus $1,000 iniciales al final más $120 adicionales de intereses devengados.
La Fórmula
La mejor manera de entender cómo se calcula el interés simple es pensar en la siguiente relación:
Monto de interés simple = Cuánto a Qué tasa de interés simple para Cuanto tiempo
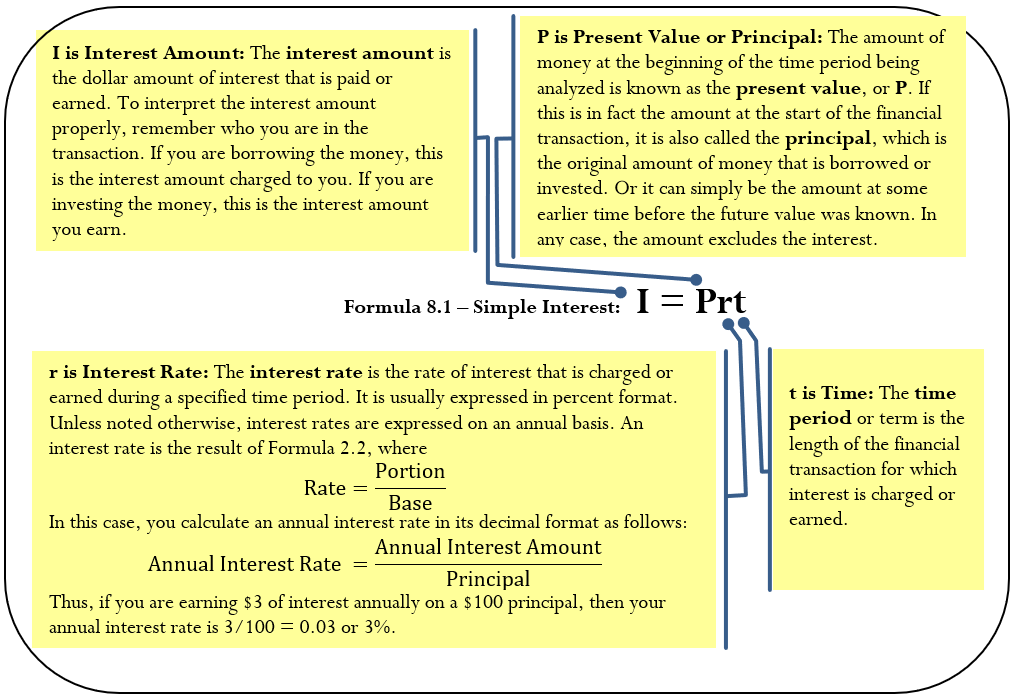
Observe que las variables clave son la cantidad, la tasa de interés simple y el tiempo. La Fórmula 8.1 combina estos elementos en una fórmula de simple interés.
Cómo funciona
Siga estos pasos cuando calcule la cantidad de interés simple:
Paso 1: La Fórmula 8.1 tiene cuatro variables, y es necesario identificar tres para cualquier cálculo que implique interés simple. Si es necesario, dibuje una línea de tiempo para ilustrar cómo se mueve el dinero a lo largo del tiempo.
Paso 2: Asegurar que la tasa de interés simple y el periodo de tiempo se expresen con una unidad común. Si no lo están ya, es necesario convertir una de las dos variables a las mismas unidades que la otra.
Paso 3: Aplicar la Fórmula 8.1 y resolver para la variable desconocida. Utilice álgebra para manipular la fórmula si es necesario.
Supongamos que tiene $500 ganando 3% de interés simple por un periodo de nueve meses. ¿Cuánto interés gana?
Paso 1: Tenga en cuenta que su principal es de $500, o\(P=\$ 500\). Se supone que la tasa de interés es anual, así\(r=3 \%\) por año. El periodo de tiempo es de nueve meses.
Paso 2: Convertir el periodo de tiempo de meses a años:\(t=\dfrac{9}{12}\).
Paso 3: De acuerdo con la Fórmula 8.1,\(I=\$ 500 \times 3 \% \times=\$ 11.25\). Por lo tanto, el monto de interés que gana sobre la inversión de $500 en el transcurso de nueve meses es de $11.25.
Notas Importantes
Recordemos que las ecuaciones algebraicas requieren que todos los términos se expresen con una unidad común. Este principio sigue siendo cierto para la Fórmula 8.1, particularmente en lo que se refiere a la tasa de interés y al periodo de tiempo. Por ejemplo, si tienes una tasa de interés anual del 3% durante nueve meses, entonces
- El tiempo debe expresarse anualmente a partir\(\dfrac{9}{12}\) de un año para igualar la tasa de interés anual, o
- La tasa de interés debe expresarse mensualmente como\(\dfrac{3\%}{12} = 0.25\%\) por mes para que coincida con el número de meses.
No importa cuál haga siempre y cuando exprese tanto la tasa de interés como el tiempo en la misma unidad. Si una de estas dos variables es su algebraica desconocida, la unidad de la variable conocida determina la unidad de la variable desconocida. Por ejemplo, suponga que está resolviendo la Fórmula 8.1 para el periodo de tiempo. Si la tasa de interés utilizada en la fórmula es anual, entonces el periodo de tiempo se expresa en número de años.
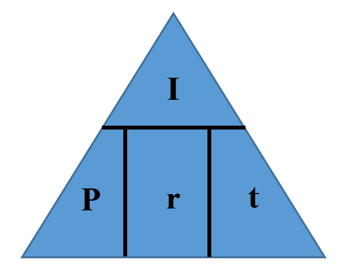
Caminos hacia el éxito
Cuatro variables están involucradas en la fórmula de interés simple, lo que significa que se pueden conocer tres cualquiera, requiriendo que resuelvas para la cuarta variable faltante. Para reducir el desorden de fórmulas, la técnica del triángulo ilustrada aquí te ayuda a recordar cómo reorganizar la fórmula según sea necesario.
- Si tienes una deuda por la que no has hecho ningún pago, sin embargo, se le está cobrando intereses simples sobre el principal, ¿adeudarías más o menos dinero en el futuro?
- Contestar
-
- Más, porque los intereses se ganan y por lo tanto se agregan a su cuenta de ahorros.
- Más, porque adeuda al principal y adeuda los intereses, lo que aumenta su monto total adeudado
Julio pidió prestado $1,100 a María hace cinco meses. Cuando primero pidió prestado el dinero, coincidieron en que pagaría a María un 5% de interés simple. Si Julio le devuelve el dinero hoy, ¿cuánto interés le debe?
Solución
Calcula la cantidad de intereses que Julio le debe a María (\(I\)).
Lo que ya sabes
Paso 1:
Los términos de su acuerdo son los siguientes:\(P = \$1,100, r = 5\%, t = 5\) meses
Cómo llegarás allí
Paso 2:
La tasa es anual, y el tiempo es en meses. Convertir el tiempo a un número anual.

Paso 3:
Aplicar Fórmula 8.1.
Realizar
Paso 2:
Cinco meses de 12 meses en un año es\(\dfrac{5}{12}\) de un año, o\(t=\dfrac{5}{12}\).
Paso 3:
\[I=\$ 1,100 \times 5 \% \times \dfrac{5}{12}=\$ 1,100 \times 0.05 \times 0.41 \overline{6}=\$ 22.92 \nonumber \]
Para que Julio le devuelva a María, debe reembolsarle el principal de $1,100 prestado más un adicional de $22.92 de simple interés según su acuerdo.
Una inversión de $3,500 obtuvo 70 dólares de interés en el transcurso de seis meses. ¿Qué tasa anual de interés simple obtuvo la inversión?
Solución
Calcular la tasa de interés anual (\(r\)).
Lo que ya sabes
Paso 1:
Se conocen el principal, el monto de interés y el tiempo:\(P = \$3,500, I = \$70, t = 6\) meses
Cómo llegarás allí
Paso 2:
La tasa de interés calculada debe ser anual, por lo que también debes expresar el periodo de tiempo anualmente.

Paso 3:
Aplicar Fórmula 8.1, reordenando para\(r\).
Realizar
Paso 2:
Seis meses de cada 12 meses en un año es\(\dfrac{6}{12}\) de un año, o\(t=\dfrac{6}{12}\).
Paso 3:
\[\$ 70=\$ 3,500 \times r \times \dfrac{6}{12} \nonumber \]
\[r=\dfrac{\$ 70}{\$ 3,500 \times \dfrac{6}{12}}=\dfrac{\$ 70}{\$ 1,750}=0.04 \text { or } 4 \% \nonumber \]
Para $3,500 para ganar $70 intereses simples en el transcurso de seis meses, la tasa de interés simple anual debe ser del 4%.
¿Qué cantidad de dinero invertido al 6% anual de interés simple durante 11 meses gana $2,035 de interés?
Solución
Calcular la cantidad de dinero originalmente invertido, que se conoce como el valor presente o principal, simbolizado por\(P\).
Lo que ya sabes
Paso 1:
Se conocen la tasa de interés, el tiempo y los intereses devengados:\(r = 6\%, t = 11\) meses,\(I = \$2,035\)
Cómo llegarás allí
Paso 2:
Convertir el tiempo de meses a una base anual para igualar la tasa de interés.

Paso 3:
Aplicar Fórmula 8.1, reordenando para\(P\).
Realizar
Paso 2:
Once meses de 12 meses en un año es\(\dfrac{11}{12}\) de un año, o\(t=\dfrac{11}{12}\).
Paso 3:
\[\$ 2,035=P \times 6 \% \times \dfrac{11}{12} \nonumber \]
\[P=\dfrac{\$ 2,035}{6 \% \times \dfrac{11}{12}}=\dfrac{\$ 2,035}{0.06 \times 0.91 \overline{6}}=\$ 37,000 \nonumber \]
Para generar $2,035 de interés simple al 6% en un plazo de 11 meses, se deben invertir $37,000.
¿Por cuántos meses se deben invertir 95,000 dólares para ganar $1,187.50 de interés simple a una tasa de interés del 5%?
Solución
Calcular el tiempo en meses (\(t\)) que toma el dinero para adquirir los intereses.
Lo que ya sabes
Paso 1:
Se conocen la cantidad de dinero invertido, los intereses devengados y la tasa de interés:\(P = \$95,000.00, I = \$1,187.50, r = 5\%\)
Cómo llegarás allí
Paso 2:
Expresa el tiempo en meses. Convertir la tasa de interés a un formato “por mes”.

Paso 3: Aplicar la Fórmula 8.1, reordenando para\(t\).
Realizar
Paso 2:
5% por año convertido en una tarifa mensual es\(r=\dfrac{0.05}{12}\)
Paso 3:
\[\$ 1,187.50=\$ 95,000 \times \dfrac{0.05}{12} \times t \nonumber \]
\[t=\dfrac{\$ 1,187.50}{\$ 95,000 \times \dfrac{0.05}{12}}=\dfrac{\$ 1,187.50}{\$ 95,000 \times 0.0041 \overline{6}}=3 \text { months } \nonumber \]
Por 95,000 dólares para ganar $1,187.50 al 5% de interés simple, se debe invertir por un periodo de tres meses.
Hora y Fechas
En los ejemplos de interés simple hasta el momento, el periodo de tiempo equivalía a un número exacto de meses. Si bien esto es conveniente en muchas situaciones, las instituciones y organizaciones financieras calculan los intereses con base en el número exacto de días en la transacción, lo que cambia el monto del interés.
Para ilustrar esto, suponga que tuvo dinero ahorrado para todos los meses de julio y agosto, dónde\(t=\dfrac{2}{12}\) o\(t=0.1\) de un año. No obstante, si se utiliza el número exacto de días, los 31 días de julio y los 31 días de agosto suman 62 días. En un año de 365 días que es\(t=\frac{62}{365} \text { or } t=0.169863\) de un año. Observe que se produce una diferencia de 0.003196. Por lo tanto, para ser precisos en la realización de cálculos simples de intereses, debe calcular el número exacto de días involucrados en la transacción.
Cómo averiguar los días
En la práctica, al contar el número de días en una transacción se incluye el primer día pero no el último día. Esto se debe a que los intereses se calculan sobre el saldo diario de cierre, no sobre los saldos intermedios a lo largo de un día. Por ejemplo, si pediste prestado $500 el 3 de junio y lo devolviste con intereses el 5 de junio, el saldo de cierre el 3 y 4 de junio es de $500. No obstante, el 5 de junio se restablece un saldo cero. Por lo tanto, usted cuenta el 3 y 4 de junio como días de interés pero no el 5 de junio, por lo que deberá dos días de interés, no tres.
Hay tres formas comunes de calcular el número de días involucrados en una transacción.
Método 1: Usa tus nudillos
Puedes usar tus nudillos como una ayuda para recordar qué meses del año tienen más o menos días.
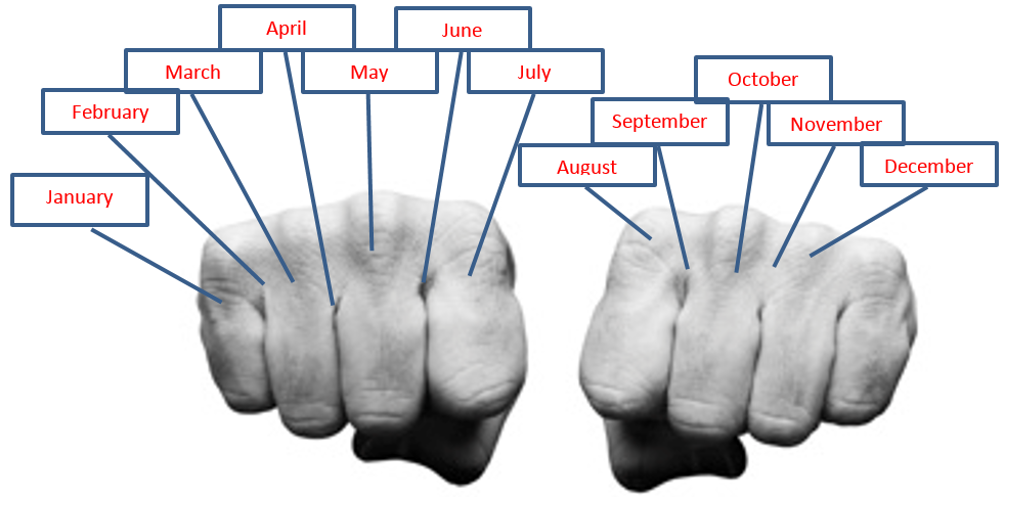
Pon tus nudillos uno al lado del otro y comienza en tu nudillo más exterior. Cada nudillo representa un mes con 31 días. Cada valle entre los nudillos representa un mes que no tiene 31 días (30 en total excepto febrero, que tiene 28 o 29). Ahora empieza a contar meses. Tu primer nudillo (meñique) es enero, que tiene 31 días. A continuación está tu primer valle, que es febrero y no tiene 31 días. Tu próximo nudillo (dedo anular) es marzo, que tiene 31 días... y así sucesivamente. Cuando llegues a tu último nudillo (tu dedo índice), muévete al primer nudillo de la otra mano (un dedo índice nuevamente). Observe que julio y agosto son los dos meses espalda con espalda con 31 días.
Si estás intentando calcular el número de días entre el 20 de marzo y el 4 de mayo, usa tus nudillos para recordar que marzo tiene 31 días y abril tiene 30 días. Los cálculos se ilustran en la tabla aquí.
| Fecha de inicio | Fecha de finalización | Días entre Fechas |
|---|---|---|
| 20 de marzo | 31 de marzo | 31 − 20 = 11 días |
| 31 de marzo (que precede al 1 de abril, por lo que es el día “0" para abril) | 30 de abril | 30 − 0 = 30 días |
| 30 de abril (que precede al 1 de mayo, por lo que es el día “0" para mayo) | 4 de mayo | 4 − 0 = 4 días |
| TOTAL | 11 + 30 + 4 = 45 días |
¿Por qué la fecha de finalización de una línea se convierte en la fecha de inicio de la siguiente línea? Recuerda que cuentas el primer día, pero no el último día. Por lo tanto, en la primera línea el 31 de marzo aún no se ha contado y se debe contar en la segunda línea. En última instancia, una transacción que se extiende del 20 de marzo al 4 de mayo implica 45 días como periodo de tiempo.
Método 2: Usar una tabla de números de serie
En la tabla de la página siguiente, a los días del año se les asigna un número de serie. El número de días entre dos fechas cualesquiera en el mismo año calendario es simplemente la diferencia entre los números de serie para las fechas.
Usando el ejemplo del Método 1, cuando las fechas estén dentro del mismo año calendario, encuentre el número de serie para la fecha posterior, el 4 de mayo (Día 124) y el número de serie para la fecha anterior, el 20 de marzo (Día 79). Después, encuentra la diferencia entre los dos números de serie (\(124-79=45\)días).
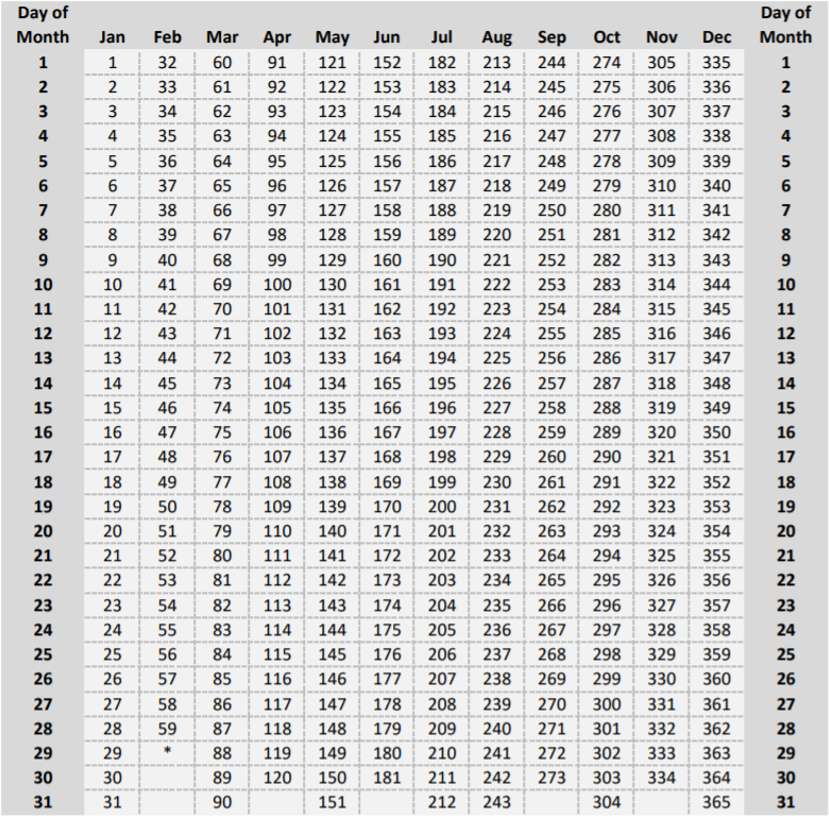
*Para los años bisiestos, el 29 de febrero se convierte en el Día 60 y el número de serie para cada día subsiguiente se incrementa en 1.
Método 3: Usar la función de fecha BAII Plus
Tu calculadora BAII Plus está programada con la capacidad de calcular el número de días involucrados en una transacción de acuerdo con el principio de contar el primer día pero no el último día. La función “Fecha” se encuentra en la segunda repisa por encima del número uno. Para utilizar esta función, abra la ventana pulsando 2nd 1.

- Desplázate entre las cuatro líneas de visualización usando tus\(\downarrow\) flechas\(\uparrow\) y. Hay cuatro variables:
- DT1 es la fecha de inicio de la transacción.
- DT2 es la fecha de finalización de la transacción.
- DBD son los días entre fechas, que es tu\(t\) en la Fórmula 8.1.
- ACT o 360 es el método de cálculo de los días entre fechas. En ACT (para “real”), la calculadora calcula el DBD con base en el número correcto de días en el mes. En 360, el DBD se basa en tratar cada mes como teniendo 30 días (\(30 \times 12=360\)días). Para todos los cálculos, establezca la calculadora en el modo ACT. Activa esta configuración presionando 2nd SET.
- Para ingresar una fecha en la calculadora, la calculadora utiliza el formato MM.DDYY donde:
- MM es el valor numérico del mes; no es necesario ingresar el cero inicial en meses con solo un dígito.
- DD es el día del mes; siempre debes ingresar este valor con dos dígitos usando un cero a la izquierda para los días 1 a 9 en un mes.
- YY son los dos últimos dígitos del año; siempre debes ingresar esto con dos dígitos. Si su pregunta no involucra un año, seleccione el año apropiado de su elección.
- Siempre y cuando conozca dos de las variables DT1, DT2 o DBD, puede calcular la tercera. Ingrese dos cualquiera de las tres variables, presionando ENTRAR después de cada una y asegurando que la ventana muestre la variable de salida que está buscando, y luego presione CPT.
Usando el ejemplo del Método 1, para calcular el tiempo del 20 de marzo al 4 de mayo primero es necesario elegir un año arbitrariamente, quizás 2011. Por lo tanto, realice la siguiente secuencia:
\[\text{2nd DATE}\nonumber \]
\[\text{2nd CLR Work (to erase previous calculations)}\nonumber \]
\[3.2011 \text{ENTER }\downarrow \text{(this is March 20, 2011)}\nonumber \]
\[5.0411 \text{ENTER }\downarrow \text{(this is May 4, 2011)}\nonumber \]
\[\text{CPT}\nonumber \]
\[\text{Answer: }45\nonumber \]
Ten en cuenta que la respuesta es la misma a la que llegaste manualmente usando tus nudillos.
Notas Importantes
Al resolver para\(t\), los decimales pueden aparecer en su solución. Por ejemplo, si se calcula\(t\) en días, la respuesta puede aparecer como 45.9978 o 46.0023 días; sin embargo, los intereses se calculan sólo en días completos. Esto ocurre porque el monto de interés (\(I\)) utilizado en el cálculo se ha redondeado a dos decimales. Dado que el monto del interés es impreciso, el cálculo de\(t\) es impreciso. Cuando esto ocurre,\(t\) redondear al entero más cercano.
Cosas a tener en cuenta
Calcular mal el número de días en febrero tiene que ser uno de los errores más comunes. Para ayudarte a recordar cuántos días hay en febrero, recuerda tu conocimiento de los años bisiestos.
- Febrero tiene 28 días excepto los años bisiestos, en los que tiene 29 días.
- Los años bisiestos son aquellos años que son uniformemente divisibles por cuatro o 400. Sin embargo, aquellos años que son uniformemente divisibles por 100 (excepto los años que son uniformemente divisibles por 400) no son años bisiestos. Aquí hay algunos ejemplos para ilustrar esta regla:
- El año 1900 no fue un año bisiesto, ya que es divisible uniformemente por 100 y no por 400.
- El año 1996 fue un año bisiesto, ya que es divisible de manera uniforme por cuatro y no por 100.
- El año 2000 fue uno de esos años de excepción, y fue un año bisiesto ya que es uniformemente divisible por 400.
- El año 2004 volvió a ser un año bisiesto ya que es divisible de manera uniforme por cuatro y no por 100. Así, en este siglo 2004, 2008, 2012, 2016, 2020, 2024, y así sucesivamente a cuatro patas son todos años bisiestos con 29 días.
- El año 2100 no será un año bisiesto, ya que es uniformemente divisible por 100.
Tenga en cuenta que cuando se trata del número total de días en un año, los cálculos simples de intereses ignoran el día 366 en un año bisiesto. Por lo tanto, supongamos que un año tiene 365 días en todos los cálculos.
Caminos hacia el éxito
Al ingresar dos fechas ya sea en la calculadora o en Excel, el orden en el que claves las fechas no es importante. Si por casualidad coloca el último día de la transacción en el primer campo (DT1 o Fecha de Inicio) y el día de inicio de la transacción en el último campo (DT2 o Fecha de finalización), entonces el número de días se computará como un número negativo ya que las fechas se invierten. Ignorar el signo negativo en estas instancias. Usando el ejemplo, en tu calculadora si habías ingresado el 4 de mayo en DT1 y el 20 de marzo en DT2, el DBD calcula como −45, en el que ignoras el signo negativo para determinar que la respuesta es de 45 días.
Azul le pidió prestados $4,200 a Hannah el 3 de noviembre de 2011. Su acuerdo requería que Azul devolviera el préstamo el 14 de abril de 2012, con 8% de interés simple. Además del director, ¿cuánto interés le debe Azul a Hannah el 14 de abril?
Solución
Calcula la cantidad de interés simple (\(I\)) que Azul le debe a Hannah en su préstamo.
Lo que ya sabes
Paso 1:
Se conocen el principal, la tasa de interés simple y las fechas:\(P = \$4,200, r = 8\%\); Fecha de inicio = 3 de noviembre de 2011; Fecha de finalización = 14 de abril de 2012
Cómo llegarás allí
Paso 1 (continuación):
Calcular el número de días en la transacción. Tenga en cuenta que esta transacción involucra febrero de 2012, que es un año bisiesto.
Paso 2:
La tarifa es anual y el tiempo es en días. Convertir el tiempo a un número anual.

Paso 3:
Aplicar Fórmula 8.1.
Realizar
Paso 1 (continuación):
| Fecha de inicio | Fecha de finalización | Días entre Fechas |
|---|---|---|
| Noviembre 3, 2011 | Noviembre 30, 2011 | 30 − 3 = 27 |
| Noviembre 30, 2011 | diciembre 31, 2011 | 31 − 0 = 31 |
| diciembre 31, 2011 | 31 de enero de 2012 | 31 − 0 = 31 |
| 31 de enero de 2012 | Febrero 29, 2012 | 29 − 0 = 29 |
| Febrero 29, 2012 | 31 de marzo de 2012 | 31 − 0 = 31 |
| 31 de marzo de 2012 | abril 14, 2012 | 14 − 0 = 14 |
| TOTAL | 27 + 31 + 31 + 29 + 31 + 14 = 163 días |
Paso 2:
163 días de 365 días en un año es\(t=\dfrac{163}{365}\)
Paso 3:
\[I=\$ 4,200 \times 8 \% \times \dfrac{163}{365}=\$ 4,200 \times 0.08 \times 0.446575=\$ 150.05 \nonumber \]
Para obtener el número de días, utilice la función FECHA:
| DT1 | DT2 | DBD | Modo |
|---|---|---|---|
| 11.0311 | 4.1412 | Respuesta: 163 | ACTO |
Azul tomó prestado el dinero por un periodo de 163 días y le debe a Hannah 150.05 dólares de simple interés sobre su préstamo, además de reembolsar el principal de $4,200.
El 13 de septiembre de 2011, Aladdin decidió devolverle al Genie su préstamo de $15,000 al 9% de interés simple. Si le pagó al Genio el principal más $1,283.42 de intereses, ¿en qué día le pidió prestado el dinero al Genio?
Solución
Para determinar la fecha de inicio, se debe calcular el tiempo involucrado en esta transacción\(t\), o,.
Lo que ya sabes
Paso 1:
Se conocen el principal, el monto de interés, la tasa de interés simple y la fecha de finalización:\(P = \$15,000.00, I = \$1,283.42, r = 9\%\); Fecha de finalización = 13 de septiembre de 2011
Cómo llegarás allí
Paso 2:
El tiempo es en días, pero la tasa es anual. Convertir la tarifa a una tarifa diaria.

Paso 3:
Aplicar Fórmula 8.1, reordenando para\(t\).
Paso 3 (continuación):
Usando la Fecha de Fin, use la t para determinar la Fecha de Inicio.
Realizar
Paso 2:
Convertir la tasa de interés a diaria:\(r=\dfrac{9 \%}{365}\).
Paso 3:
\[t=\dfrac{\$ 1,283.42}{\$ 15,000 \times \dfrac{0.09}{365}}=346.998741 \text { days } \rightarrow 347 \text { days } \nonumber \]
Paso 3 (continuación):
El número de días es cercano a un año. Retrocede 365 días e inicia el 13 de septiembre de 2010. Observe que 347 días es 365 − 347 = 18 días cortos de un año completo. Sumando 18 días al 13 de septiembre de 2010, equivale al 1 de octubre de 2010. Esta es la fecha de inicio.
Instrucciones de la calculadora
Para calcular la fecha de inicio, utilice la función FECHA:
| DT1 | DT2 | DBD | Modo |
|---|---|---|---|
| Respuesta: 01/10/2010 | 9.1311 | 347 | ACTO |
Si Aladdin le debía al Genie $1,283.42 de simple interés al 9% sobre un principal de $15,000, debió haber tomado prestado el dinero 347 días antes, que es el 1 de octubre de 2010.
Tasas de interés variables
No todas las tasas de interés se mantienen constantes. Hay dos tipos de tasas de interés:
- Fijo. Una tasa de interés fija es una tasa de interés que no se modifica durante la duración de la transacción.
- Variable. Una tasa de interés variable es una tasa de interés que está abierta a fluctuaciones a lo largo de la duración de una transacción. Esta tasa de interés variable suele estar vinculada a la tasa prima, que es una tasa de interés establecida por el Banco de Canadá que suele formar la tasa de préstamo más baja para los préstamos más seguros. A la mayoría de las personas y empresas se les suele cobrar la tasa prime más un porcentaje (típicamente 0.5% a 5%) para llegar a la tasa de interés variable. El Banco de Canadá ajusta periódicamente esta tasa debido a consideraciones económicas y financieras en Canadá.
En todos los ejemplos anteriores de esta sección, se fijó la tasa de interés (\(r\)) durante la duración de la transacción. Cuando\(r\) fluctúa, debes romper la pregunta en periodos de tiempo o fragmentos de tiempo para cada valor de\(r\). En cada uno de estos fragmentos de tiempo, se calcula la cantidad de interés simple ganado o cargado y luego suma los montos de interés para formar el total de los intereses devengados o cobrados.
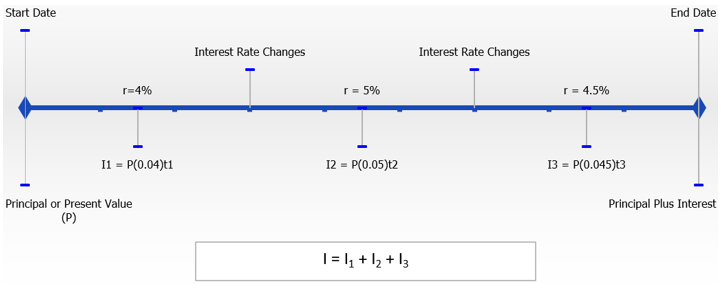
Esta cifra ilustra este proceso con una tasa variable que cambia dos veces en el transcurso de la transacción. Para calcular el monto total de interés, es necesario ejecutar la Fórmula 8.1 para cada uno de los fragmentos de tiempo. Después, totalizar los montos de interés de cada uno de los tres fragmentos de tiempo para calcular el monto de interés (\(I\)) para toda la transacción.
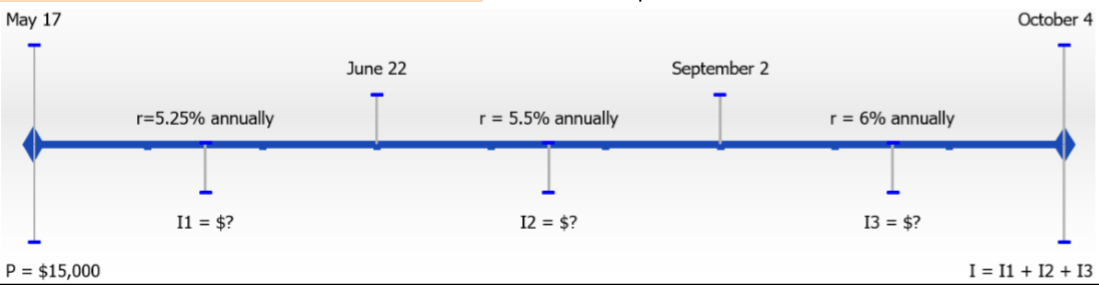
Julio tomó prestados 10,000 dólares el 17 de mayo a una tasa de interés variable de prime + 3% cuando la tasa prime era de 2¼%. El 22 de junio la tasa prime aumentó ¼%, y el 2 de septiembre volvió a aumentar ½%. ¿Cuánto interés pagará Julio cuando devuelva su préstamo el 4 de octubre?
Solución
Calcular la cantidad de intereses que Julio debe por todo el periodo de tiempo de su préstamo, o bien\(I\), del 17 de mayo al 4 de octubre.
Lo que ya sabes
Paso 1:
Hay una tasa de interés inicial y luego cambia dos veces en el transcurso de la transacción. Eso significa que hay tres periodos de tiempo y tres tipos de interés diferentes. El principal también se conoce:\(P = \$10,000\).
| Fecha | Tasa de interés |
|---|---|
| Del 17 de mayo al 22 de junio | 2¼% + 3% = 5¼% |
| 22 de junio al 2 de septiembre | 5¼% + ¼% = 5½% |
| Septiembre 2 a Octubre | 4 5½% + ½% = 6% |
Cómo llegarás allí
Paso 1 (continuación):
Calcular el número de días para cada uno de los tres periodos de tiempo.
Paso 2:
Las tarifas son anuales mientras que cada una de las horas son en días. Convertir cada una de las veces a un número anual.
Paso 3:
Para cada periodo de tiempo, aplique la Fórmula 8.1.
Paso 3 (continuación):
Suma los tres montos de interés para llegar al total de los intereses pagados.
| Fechas | Cálculos | Número total de días | Convertir\(t\) a anual | Calcular interés |
|---|---|---|---|---|
| Paso 1 (continuación) | \ (t\) a anual” style="vertical-align:middle; "> Paso 2 | Paso 3 | ||
| Del 17 de mayo al 22 de junio | 17 de mayo al 31 de mayo = 14 días 31 de mayo al 22 de junio = 22 días | 14 + 22 = 36 días | \ (t\) a anual” style="vertical-align:middle; ">\(\dfrac{36}{365}\) | \ (\ begin {alineado} I_ {1} &=\ $15,000 (0.0525)\ izquierda (\ dfrac {36} {365}\ derecha)\\ &=\ $77.671232 \ end {alineado}\) |
| 22 de junio al 2 de septiembre | 22 de junio al 30 de junio = 8 días 30 de junio al 31 de julio = 31 días 31 de julio al 31 de agosto = 31 días 31 de agosto al 2 de septiembre = 2 días | 8 + 31 + 31 + 2 = 72 días |
\ (t\) a anual” style="vertical-align:middle; ">\(\dfrac{72}{365}\) | \ (\ begin {alineado} I_ {2} &=\ $15,000 (0.055)\ izquierda (\ dfrac {72} {365}\ derecha)\\ &=\ $162.739726 \ end {alineado}\) |
| Septiembre 2 a Octubre 4 | 2 de septiembre a 30 de septiembre = 28 días 30 de septiembre al 4 de octubre = 4 días | 28 + 4 = 32 | \ (t\) a anual” style="vertical-align:middle; ">\(\dfrac{32}{365}\) | \ (\ begin {alineado} I_ {3} &=\ $15,000 (0.06)\ izquierda (\ dfrac {32} {365}\ derecha)\\ &=\ $78.904109 \ end {alineado}\) |
| \ (t\) a anual” rowspan="1" style="vertical-align:middle; "> Paso 3 (continuación): TOTAL | $319.32 | |||
Instrucciones de la calculadora
Escoja arbitrariamente el año 2011 y utilice la función DATE:
| Fragmento de tiempo | DT1 | DT2 | DBD | Modo |
|---|---|---|---|---|
| 1 | 5.1711 | 6.2211 | Respuesta: 36 | ACTO |
| 2 | 6.2211 | 9.0211 | Respuesta: 72 | ACTO |
| 3 | 9.0211 | 10.0411 | Respuesta: 32 | ACTO |
Julio debe $319.32 de simple interés en su fecha de reembolso del 4 de octubre.


