8.2: Mover dinero con intereses simples
- Page ID
- 110790
¿Se puede calcular la cantidad de dinero requerida para cumplir una meta futura? Asume que graduarás la universidad con tu diploma de administración de empresas en unos meses y ya te has registrado en tu universidad local para continuar con tus estudios hacia una licenciatura en comercio. Estimas tu matrícula total, cuotas y libros de texto en $8,000. Después de investigar algunas inversiones a corto plazo, encuentra que la mejor tasa de interés simple que se puede obtener es 4.5%. ¿Cuánto dinero debes invertir hoy para que crezca con interés al dinero de colegiatura necesario?
En el apartado anterior, calculaste la cantidad de intereses devengados o cobrados sobre una inversión o préstamo. Si bien es bueno saber este número, la mayoría de las veces los inversionistas están interesados únicamente en cuánto en total, incluyendo tanto el principal como los intereses, se adeuda o se ahorra. Además, para calcular el monto de interés en la Fórmula 8.1, debes conocer el principal. Cuando las personas planean para el futuro, conocen la cantidad futura de dinero que necesitan pero no saben cuánto dinero deben invertir hoy para llegar a esa meta. Este es el caso en el ejemplo de apertura anterior, por lo que necesita una técnica adicional para manejar el interés simple.
Esta sección explora cómo calcular el principal y el interés juntos en un solo cálculo. Agrega la flexibilidad de averiguar cuánto dinero hay al inicio del periodo de tiempo siempre y cuando conozcas el valor al final, o viceversa. De esta manera, se puede resolver casi cualquier situación de interés simple.
Valor de Vencimiento (o Valor Futuro)
El valor de vencimiento de una transacción es la cantidad de dinero resultante al final de una transacción, cantidad que incluye tanto el interés como el principal juntos. Se le llama valor de vencimiento porque en el mundo financiero la terminación de una transacción financiera se conoce como el “vencimiento” de la transacción. El monto del principal con intereses en algún momento en el futuro, pero no necesariamente al final de la transacción, se conoce como el valor futuro.
La Fórmula
Para cualquier transacción financiera que implique intereses simples, es cierto lo siguiente:
\[\text{Amount of money at the end }=\text{ Amount of money at the beginning }+\text{ Interest}\nonumber \]
Aplicando álgebra, puede resumir esta expresión mediante la siguiente ecuación, donde el valor futuro o valor de madurez se denota comúnmente con el símbolo\(S\):
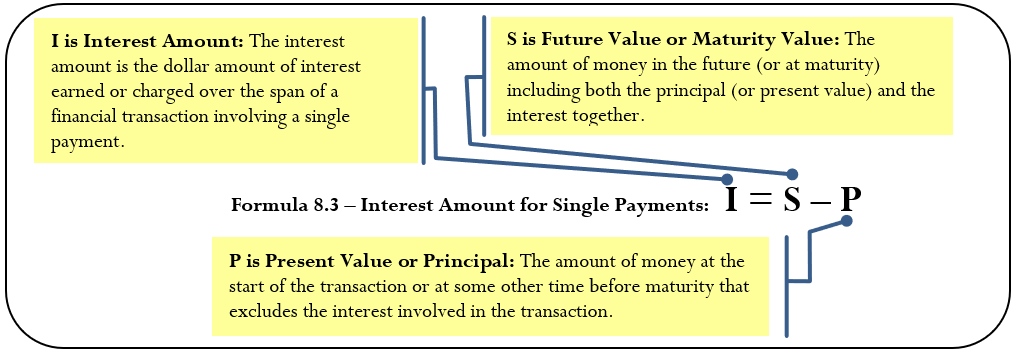
\[S=P+I\nonumber \]
Sustituyendo en la Fórmula 8.1,\(I = Prt\), produce la ecuación
\[S=P+Prt\nonumber \]
Simplifique esta ecuación factorizando\(P\) en el lado derecho para llegar a la Fórmula 8.2.
Dependiendo del escenario financiero, qué información conoce y qué variable necesita calcular, es posible que necesite una segunda fórmula que ofrezca un método alternativo para calcular el monto en dólares de interés simple.
Cómo funciona
Siga estos pasos cuando trabaje con pagos únicos que involucren intereses simples:
Paso 1: La Fórmula 8.2 tiene cuatro variables, tres cualquiera de las cuales debes identificar para trabajar con un solo pago que implique intereses simples.
- Si falta el\(P\) o pero\(S\)\(I\) se conoce el, aplique la Fórmula 8.3 para determinar el valor desconocido.
- Si solo\(I\) se conoce el monto de interés y ni se identifica\(P\) ni\(S\) se identifica, recuerde que el monto de interés es una porción y que la tasa de interés es producto de tasa y tiempo (por ejemplo, 6% anual durante nueve meses es una tasa de interés devengada de 4.5%). Aplicar la Fórmula 2.2 en tasa, porción y base para resolver por base, que es el valor presente o\(P\).
- Si es necesario, dibuje una línea de tiempo para ilustrar cómo se mueve el dinero a través del tiempo.
Paso 2: Asegurar que la tasa de interés simple y el periodo de tiempo se expresen con una unidad común. Si no es así, es necesario convertir una de las dos variables para lograr lo común.
Paso 3: Aplicar la Fórmula 8.2 y resolver para la variable desconocida, manipulando la fórmula según sea necesario.
Paso 4: Si necesita calcular el monto de los intereses, aplique la Fórmula 8.3.
Supongamos que hoy tienes $10,000 que vas a invertir al 7% de interés simple durante 11 meses. ¿Cuánto dinero vas a tener en total al final de los 11 meses? ¿Cuánto interés gana?
Paso 1: El principal es\(P = \$10,000\), la tasa de interés simple es 7% anual, o\(r= 0.07\), y el tiempo es\(t = 11\) meses.
Paso 2: El tiempo es en meses, pero para igualar la tasa se necesita expresar anualmente como\(t=\dfrac{11}{12}\).
Paso 3: Aplicar la Fórmula 8.2 para calcular el valor futuro incluyendo los intereses,
\(S=\$ 10,000 \times(1+0.07 \times)=\dfrac{11}{12}\$ 10,641.67\). Esta es la cantidad total después de 11 meses.
Paso 4: Aplicar la Fórmula 8.3 para calcular los intereses devengados,\(I=\$ 10,641.67-\$ 10,000.00=\$ 641.67\). También podrías aplicar la Fórmula 8.1 para calcular el monto del interés; sin embargo, la Fórmula 8.3 es mucho más fácil de usar. Los 10.000 dólares ganan 641.67 dólares en interés simple durante los próximos 11 meses, resultando en 10.641.67 dólares en total.
Cosas a tener en cuenta
Al igual que con la Fórmula 8.1, el error más común en la aplicación de la Fórmula 8.2 es no asegurar que la tasa y el tiempo se expresen en las mismas unidades. Antes de continuar, ¡comprueba siempre estas dos variables!
Caminos hacia el éxito
Al resolver la Fórmula 8.2 tanto por tasa como por tiempo, generalmente es más fácil usar la Fórmula 8.3 y la Fórmula 8.1 en su lugar. Siga estos pasos para resolver por tarifa o tiempo:
- Si se le ha proporcionado tanto el valor presente como el valor futuro, aplique la Fórmula 8.3 para calcular el monto de interés (\(I\)).
- Aplique y reorganice la Fórmula 8.1 para resolverla por tarifa o tiempo según sea necesario.
En cada una de las siguientes situaciones, determinar qué enunciado es correcto.
- Si tienes un valor futuro de $5,000 y hay intereses involucrados, entonces tu valor actual es
- Más de $5,000
- El mismo
- Menos de $5,000
- Si tuviste un capital de $10,000 ganando 10% de interés simple por cualquier periodo menor a un año, ganas
- Más de $1,000 de interés
- Exactamente $1,000 intereses
- Menos de $1,000 de interés
- Si tomaste un préstamo por $2,500 a una tasa de interés simple del 5% por seis meses y no hiciste pagos durante ese período de tiempo, debes
- Más de $2,500
- Exactamente $2,500
- Menos de $2,500
- Responder
-
- Menos de $5,000. Al cobrar o ganar intereses, el valor presente siempre es menor que el valor futuro.
- Menos de $1,000 de interés. Los $10,000 ganan exactamente $1,000 intereses por año, por lo que cualquier período de tiempo inferior a un año produce una cantidad de interés menor.
- Más de $2,500. Cuando se cobran intereses, el valor futuro siempre es mayor que el valor actual
Acabas de heredar 35.000 dólares del patrimonio de tu tío y planeas comprar una casa dentro de cuatro meses a partir de hoy. Si usas tu herencia como pago inicial de la casa, ¿cuánto podrás poner si tu dinero gana 4¼% interés simple? ¿Cuánto interés te habrás ganado?
Solución
Calcular la cantidad de dinero dentro de cuatro meses incluyendo tanto el principal como los intereses devengados. Este es el valor de vencimiento (\(S\)). También calcular los intereses devengados (\(I\)).
Lo que ya sabes
Paso 1:
Se conocen el principal, la tasa de interés y el marco temporal:\(P = \$35,000, r = 4¼\%\) por año\(t = 4\) meses
Cómo Llegarás
Paso 2:
Si bien la tasa es anual, el tiempo es en meses. Convertir el tiempo a un número anual.
Paso 3:
Aplicar Fórmula 8.2.
Paso 4:
Aplicar la Fórmula 8.3 para calcular el monto del interés.
Realizar
Paso 2:
Cuatro meses de cada 12 meses en un año es\(t=\dfrac{4}{12}\)
Paso 3:
\[S=\$ 35,000 \times\left(1+4\dfrac{1}{4} \% \times \dfrac{4}{12}\right)=\$ 35,000 \times(1+0.0425 \times 0 . \overline{3})=\$ 35,495.83 \nonumber \]
Paso 4:
\[I = \$35,495.83 − \$35,000.00 = \$495.83 \nonumber \]
Dentro de cuatro meses tendrás $35,495.83 como pago inicial hacia tu casa, lo que incluye $35,000 en principal y $495.83 de intereses.
Recuerda el abridor de sección, donde necesitabas $8,000 para la matrícula en el otoño y la mejor tasa de interés simple que pudiste encontrar fue de 4.5%. Asume que tienes ocho meses antes de que necesites pagar tu colegiatura. ¿Cuánto dinero necesitas para invertir hoy?
Solución
Calcula la cantidad principal de dinero hoy (\(P\)) que debes invertir de tal manera que gane intereses y termine en los $8,000 requeridos para la colegiatura.
Lo que ya sabes
Paso 1:
Se conocen el valor futuro, la tasa de interés y el período de tiempo:\(S = \$8,000, r = 4.5\%\) por año\(t = 8\) meses
Cómo Llegarás
Paso 2:
Si bien la tasa es anual, el tiempo es en meses. Convertir el tiempo a un número anual.
Paso 3:
Aplicar Fórmula 8.2, reordenando para\(P\).
Realizar
Paso 2:
Ocho meses de 12 meses en un año es\(t=\dfrac{8}{12}\)
Paso 3:
\[\begin{aligned} &\$ 8,000=P\left(1+4.5 \% \times \dfrac{8}{12}\right)\\ &P=\dfrac{\$ 8,000}{(1+0.045 \times 0.\overline {6})}=\$ 7,766.99 \end{aligned} \nonumber \]
Si coloca $7,766.99 en la inversión, crecerá a $8,000 en los ocho meses.
Estás sentado en una oficina de tu institución financiera local el 4 de agosto. El oficial bancario te dice: “Te haremos mucho. Si adelantamos esa línea de crédito y hoy pides prestados 20,000 dólares, cuando quieras reembolsar ese saldo el 1 de septiembre solo tendrás que pagarnos $20,168.77, ¡lo que no es mucho más!” Antes de responder, decide evaluar la declaración. Calcular la tasa de interés simple que el funcionario bancario utilizó en sus cálculos.
Solución
Determine la tasa de interés que se le cobraría en su línea de crédito, o\(r\).
Lo que ya sabes
Paso 1:
Se conocen el principal, el monto de vencimiento y el período de tiempo: 4\(P = $20,000.00, S = $20,168.77, t =\) de agosto al 1 de septiembre
Cómo Llegarás
Paso 1 (continuación):
Calcular el número de días en la transacción.
Paso 2:
Dado que las tasas de interés suelen expresarse anualmente, convierte el tiempo de días a un número anual.
Paso 3:
Usa la combinación de Fórmula 8.3 y Fórmula 8.1. Primero calcule el monto de interés usando la Fórmula 8.3.
Paso 3 (continuación):
Después aplique la Fórmula 8.1, reordenando para\(r\).
Realizar
Paso 1 (continuación):
| Fecha de inicio | Fecha de Finalización | Días entre Fechas |
|---|---|---|
| 4 de agosto | 31 de agosto | 31 − 4 = 27 |
| 31 de agosto | 1 de septiembre | 1 − 0 = 1 |
| TOTAL | 27 + 1 = 28 días | |
Paso 2:
28 días de 365 días en un año es\(t=\dfrac{28}{365}\)
Paso 3:
\[I = \$20,168.77 − \$20,000.00 = \$168.77 \nonumber \]
Paso 3 (continuación):
\[r=\dfrac{\$ 168.77}{\$ 20,000.00 \times \dfrac{28}{365}}=0.110002 \text { or } 11.0002 \% \nonumber \]
Instrucciones de la calculadora
Asumir el año 2011 y utilizar la función DATE:
| DT1 | DT2 | DBD | Modo |
|---|---|---|---|
| 08.0411 | 09.0111 | Respuesta: 28 | ACTO |
La tasa de interés en la línea de crédito ofrecida es de 11.0002% (tenga en cuenta que probablemente sea exactamente 11%; lo más probable es que el extra 0.0002% se deba al monto redondeado de interés utilizado en el cálculo).
Pagos equivalentes
La vida pasa. A veces los planes financieros mejor establecidos no se cumplen. Quizás has perdido tu trabajo. A lo mejor un conductor imprudente totalizó tu vehículo, que ahora tienes que reemplazar a un gasto que debes luchar para que se ajuste a tu presupuesto. No importa el motivo, se encuentra incapaz de hacer el pago de su deuda como se prometió.
En el lado positivo, tal vez acabas de recibir una gran herencia inesperadamente. ¿Y si compraste un boleto rasca y acabas de ganar $25,000? Ahora que tienes el dinero, tal vez quieras pagar esa deuda antes de tiempo. ¿Se puede hacer?
Ya sea pagando con retraso o temprano, cualquier monto pagado debe ser equivalente a la obligación financiera original. Como has aprendido, cuando mueves dinero hacia el futuro acumula intereses simples. Cuando mueves dinero al pasado, los intereses simples deben ser removidos del dinero. Este principio se aplica tanto a pagos anticipados como atrasados:
- Pagos atrasados. Si una deuda se paga con retraso, entonces se debe imponer una sanción económica que sea justa para ambas partes involucradas. Esa penalización debe reflejar una tasa de interés vigente y agregarse al pago original. Supongamos que le debes $100 a tu amigo y que una tasa justa actual de interés simple es del 10%. Si paga esta deuda con un año de retraso, entonces se debe agregar una multa por intereses atrasados del 10% de $10, haciendo que su pago de deuda sea de 110 dólares. Esto no es diferente de que tu amigo reciba los $100 hoy e invirtiéndolo él mismo al 10% de interés para que se acumule a 110 dólares en un año.
- Pagos Anticipados. Si una deuda se paga anticipadamente, debería haber algún incentivo financiero (de lo contrario, ¿por qué molestarse?). Por lo tanto, un beneficio de interés, uno que refleje una tasa de interés actual sobre el pago anticipado, debe deducirse del pago original. Asume que le debes a tu amigo 110 dólares dentro de un año y que una tasa justa actual de interés simple es del 10%. Si paga esta deuda hoy, entonces se debe deducir un beneficio de interés anticipado del 10% de $10, haciendo su pago de deuda hoy $100. Si tu amigo entonces invierte este dinero al 10% de interés simple, dentro de un año tendrá los 110 dólares, que es lo que se suponía que debías pagar.
Observe en estos ejemplos que una tasa de interés simple del 10% significa $100 hoy es lo mismo que tener 110 dólares dentro de un año. Esto ilustra el concepto de que dos pagos son pagos equivalentes si, una vez que se tiene en cuenta una tasa de interés justa, tienen el mismo valor el mismo día. Así, en general estás encontrando dos montos en distintos momentos del tiempo que tienen el mismo valor, como se ilustra en la siguiente figura.
Cómo funciona
Los pasos requeridos para calcular un pago equivalente no son diferentes a los de los pagos únicos. Si se está realizando un pago anticipado, entonces usted conoce el valor futuro, por lo que resuelve para el valor presente (que elimina los intereses). Si se está realizando un pago atrasado, entonces usted conoce el valor presente, por lo que resuelve para el valor futuro (lo que suma la penalización de interés).
Caminos hacia el éxito
Ser financieramente inteligente significa prestar atención a cuando realizas tus pagos de deuda. Si no recibe ningún beneficio económico por realizar un pago anticipado, entonces ¿por qué hacerlo? La elección prudente es quedarse con el dinero usted mismo, invertirlo a la mejor tasa de interés posible y pagar la deuda cuando venza. ¡Cualquiera que sea el interés que se gane es suyo para mantener y aún así cumple con sus obligaciones de deuda de manera oportuna!
Erin le debe hoy 1.500 dólares a Charlotte. Desafortunadamente, Erin tuvo algunos gastos inesperados y no puede hacer el pago de su deuda. Después de discutir el tema, coinciden en que Erin puede hacer el pago nueve meses de retraso y que una tasa de interés simple justa sobre el pago atrasado es del 5%. ¿Cuánto necesita pagar Erin dentro de nueve meses? ¿Cuál es el monto de su penalización tardía?
Solución
Un pago atrasado es un monto de valor futuro (\(S\)). La penalización tardía es igual al interés (\(I\)).
Lo que ya sabes
Paso 1:
Se conocen el pago de hoy, la tasa de interés acordada y el tiempo de demora en el pago:\(P = \$1,500, r = 5\%\) anualmente,\(t = 9\) meses
Cómo Llegarás
Paso 2:
Si bien la tasa es anual, el tiempo es en meses. Convertir el tiempo a un número anual.
Paso 3:
Aplicar Fórmula 8.2.
Paso 4:
Aplicar la Fórmula 8.3 para calcular el monto de la multa por intereses atrasados.
Realizar
Paso 2:
Nueve meses de cada 12 meses en un año es\(t=\dfrac{9}{12}\).
Paso 3:
\[S=\$ 1,500 \times\left(1+5 \% \times \dfrac{9}{12}\right)=\$ 1,500 \times(1+0.05 \times 0.75)=\$ 1,556.25 \nonumber \]
Paso 4:
\[I = \$1,556.25 − \$1,500.00 = \$56.25 \nonumber \]
El pago atrasado de Erin es de $1,556.25, que incluye una multa de interés de $56.25 por realizar el pago con nueve meses de retraso.
Rupert le debe a Aminata dos pagos de deuda: 600 dólares dentro de cuatro meses y 475 dólares a partir de ahora once meses. Rupert entró hoy en algo de dinero y le gustaría pagar ambas deudas de inmediato. Aminata ha coincidido en que una tasa de interés justa es del 7%. ¿Qué cantidad debería pagar hoy Rupert? ¿Cuál es el monto total de su beneficio de pago anticipado?
Solución
Un pago anticipado es un monto de valor presente (\(P\)). Ambos pagos se trasladarán al día de hoy y se sumarán. El beneficio de pago anticipado será el monto total de los intereses retirados (\(I\)).
Lo que ya sabes
Paso 1:
Se conocen los dos pagos, la tasa de interés y las fechas de vencimiento de los pagos:\(r = 7\%\) anualmente
Primer pago:\(S = \$600, t = 4\) meses a partir de ahora
Segundo Pago:\(S = \$475, t = 11\) meses a partir de ahora
El pago de reemplazo se está realizando hoy.
Cómo Llegarás
Realiza los pasos 2 y 3 para cada pago:
Paso 2:
Si bien la tasa es anual, el tiempo es en meses. Convertir el tiempo a un número anual.
Paso 3:
Aplica la Fórmula 8.2, reordenándola para resolverla\(P\). Una vez calculas ambos\(P\), se pueden sumar para llegar al pago total.
Paso 4:
Para cada pago, aplique la Fórmula 8.3 para calcular el beneficio de interés anticipado asociado. Total de los dos valores de\(I\) para obtener el beneficio de interés temprano en general.
Realizar
Pago #1:
Paso 2:
Cuatro meses de cada 12 meses en un año es\(t=\dfrac{4}{12}\)
Paso 3:
\[\begin{aligned} \$ 600&=P\left(1+7 \% \times \dfrac{4}{12}\right)\\ P&=\dfrac{\$ 600}{(1+0.07 \times 0.\overline3)}\\ & =\$ 586.32 \end{aligned} \nonumber \]
Pago #2:
Paso 2:
Once meses de 12 meses en un año es\(t=\dfrac{11}{12}\)
Paso 3:
\[\begin{aligned} &\$ 475=P\left(1+7 \% \times \dfrac{11}{12}\right)\\ &P=\dfrac{\$ 475}{(1+0.07 \times 0.91 \overline{6})}=\$ 446.36 \end{aligned} \nonumber \]
Totales:
\(P\)hoy\(= $586.32 + $446.36 = $1,032.68\)
Paso 4:
Pago #1:\(I=S–P = $600 – $586.32 = $13.68 \)
Pago #2:\(I=S–P = $475 – $446.36 = $28.64 \)
\[I = \$13.68 + \$28.64 = \$42.32 \nonumber \]
Para liquidar ambas deudas hoy, Rupert paga $1,032.68, lo que refleja una reducción del beneficio de intereses de 42.32 dólares por el pago anticipado.