10.5: Aplicación - Inflación, Poder de Compra y Tasas de Cambio
- Page ID
- 110946
¿Cuánto recorta la inflación en los ingresos y la riqueza de las personas? En 1955, el promedio canadiense w orker ganaba un salario bruto anual de alrededor de $2,963.1 Para 2010, el trabajador canadiense promedio trajo a casa ingresos brutos anuales aproximados a $44,366.2 ¿Significa esto que los canadienses de hoy son 15 veces más ricos que nuestros abuelos? De discusiones anteriores en la sección 4.3 sobre inflación, ingresos reales y poder adquisitivo, ya se puede decir que no lo somos. El incremento real es en algo menos de 15 veces. Pero, ¿cuánto menos es?
Para responder a la pregunta, hay que expresar ambos ingresos con referencia al mismo año. O convertir los ingresos de 1955 a su equivalente en 2010 o viceversa. Para ayudar, ¿y si te dicen que la tasa de inflación de 1955 a 2010 promedió 3.91% 3 anuales? Para convertir, podrías usar el método de cambio porcentual o el método de ingreso real. Cada uno de estos plantea problemas, aunque:
• Para usar la fórmula de cambio porcentual de la sección 3.1, ¡tendrías que aplicarla 55 veces consecutivas! Claramente, esto no es práctico.
• Para utilizar la fórmula de ingresos reales de la sección 4.3, se necesitarían los números del índice de precios al consumidor para ambos años. Localizar los valores de IPC puede llevar mucho tiempo, especialmente durante años en el pasado distante. Otra complicación es que si se quiere proyectar valores futuros (como el ingreso equivalente en, digamos, 2020 en vez de 2010), los valores de IPC no existen para años futuros.
¡Tiene que haber una manera más fácil! En esta sección, verá cómo adaptar los conceptos y fórmulas de interés compuesto para adecuarse a aplicaciones tales como inflación, poder adquisitivo e incluso cambio porcentual.
Inflación
La inflación es el movimiento general al alza de los precios de los productos en una economía. Se mide por el cambio positivo en el índice de precios al consumidor. Las tasas históricas de inflación en Canadá se ilustran en la siguiente figura.
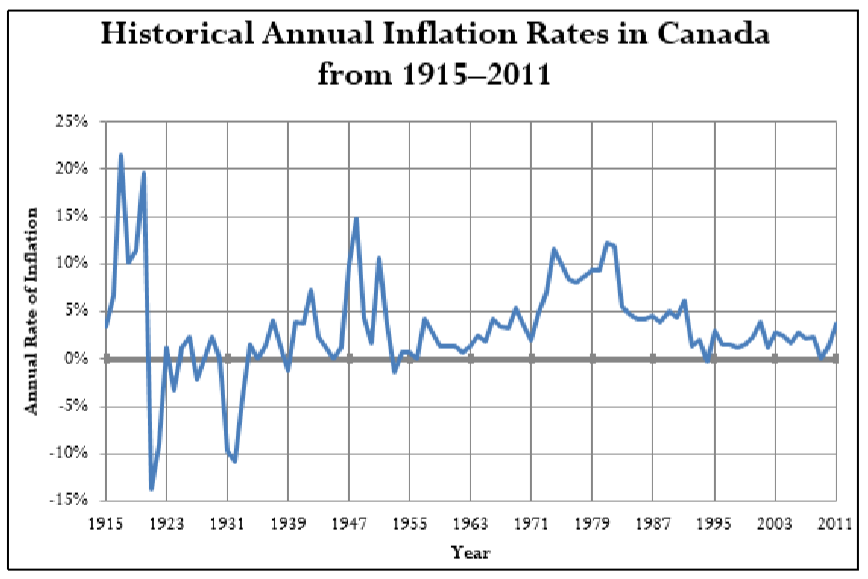
Tenga en cuenta que históricamente los precios siempre han subido a largo plazo. A corto plazo, sin embargo, ha habido periodos durante los cuales los precios se movieron a la baja. Esto se conoce como deflación, que se mide por el cambio negativo en el índice de precios al consumidor. Tales periodos de deflación generalmente no duran mucho; el periodo más largo registrado fue durante la Gran Depresión. Más recientemente, la deflación ocurrió durante algunos meses en 2009.
La inflación se expresa más comúnmente como una tasa anual; por lo tanto, la tratas matemáticamente como una tasa de interés compuesta anual. Esta es la tasa de interés nominal (\(IY\)) con una frecuencia de capitalización de uno, o\(CY\) = 1. Tenga en cuenta que si se ha producido deflación durante el periodo de tiempo en cuestión, la tasa de interés es un número negativo. Si tienes una serie de tasas de inflación, tratas esto como una tasa de interés variable. Si estás encontrando una tasa de inflación promedio por algún periodo de tiempo, tratas esto como encontrar la tasa de interés fija equivalente. Al usar las fórmulas de interés compuesto, asigne el valor presente a cualquier valor inicial en el problema en cuestión, mientras que el valor futuro es cualquier valor final. El número de períodos compuestos (\(N\)) aún refleja el número de compuestos entre los dos valores.
Cómo funciona
Se puede utilizar cualquiera de las fórmulas y técnicas del Capítulo 9 para trabajar con la inflación. El ejemplo inicial de ingresos en 1955 y 2010 ilustrará los procesos.
Resolviendo para el valor futuro
Si la variable desconocida es un valor final, aplique la Fórmula 9.3, resolviendo para el valor futuro. Si sólo se aplica una tasa de inflación (una tasa fija), esto requiere sólo una aplicación de la fórmula. Si la tasa de inflación cambia con el tiempo, aplica la fórmula varias veces o usa el método rápido de cálculo:
\[FV=PV \times\left(1+i_{1}\right)^{N_{1}} \times\left(1+i_{2}\right)^{N_{2}} \times \ldots \times\left(1+i_{n}\right)^{N_{n}} \nonumber \]
En el ejemplo, podrías trasladar los ingresos de 1955 a 2010. En este caso, el\(PV\) = $2,963,\(IY\) = 3.91%,\(CY\) = 1, y\(N\) = 55. Con una tasa de interés fija, aplicar la Fórmula 9.3 y calcular\(FV = $2,963(1 + 0.0391)^{55} = $24,427.87\). Por lo tanto, el ingreso equivalente 2010 de 1955 es de aproximadamente $24,427. Tenga en cuenta que los ingresos reales de 2010 son alrededor de 81% más altos, lo que implicaría que los canadienses se han vuelto más ricos de hecho.
Resolviendo para Valor Presente
Si la variable desconocida es un valor inicial, aplique la Fórmula 9.3, reordenando para el valor presente. Dependiendo de si la tasa de inflación es fija o variable, resuelva utilizando la misma técnica que para el valor futuro. En el ejemplo, podrías trasladar los ingresos de 2010 a 1955. En este caso, el\(FV\) = $44,366,\(IY\) = 3.91%,\(CY\) = 1, y\(N\) = 55. Con una tasa de interés fija, aplicar la Fórmula 9.3, reordenando y calculando\(PV\) = $44,366 ÷ (1 + 0.0391) 55 = $5,381.41.\(PV\) Por lo tanto, el ingreso equivalente de 1955 de 2010 es de aproximadamente $5,381. Tenga en cuenta que este ingreso es el mismo porcentaje (81%) superior al ingreso real de 1955, como encontró por el primer método.
Resolviendo para la Tarifa
Si la tasa de inflación promedio es la variable desconocida, entonces se deben conocer los valores de inicio y fin. En el ejemplo, supongamos que se desconoce la tasa de inflación promedio, pero se conocen los ingresos equivalentes de\(PV\) =2.963 dólares en 1955 y\(FV\) = $24,427.87 en 2010. El\(CY\) = 1 y\(N\) = 55 años. La aplicación de la Fórmula 9.3 da como resultado\(\$24,427.87 = \$2,963(1 + i)^{55}\). Resolviendo para\(i\) ti obtiene 3.91%. Esta es la tasa de inflación promedio (ya que\(CY\) = 1, entonces\(i = IY\)).
Resolviendo para el Término
Si la variable desconocida es la cantidad de tiempo entre los valores inicial y final, una vez más aplique la Fórmula 9.3 y reorganice para\(N\). En el ejemplo, supongamos que se conocen los valores inicial y final de\(PV\) = $2,963 en 1955 y\(FV\) = $24,427.87, pero se desconoce el año para el valor futuro. El\(IY\) = 3.91% y\(CY\) = 1. Aplicar la Fórmula 9.3 te da\(\$24,427.87 = $2,963(1 + 0.0391)^N\). Resolviendo para\(N\) da 55 años. El año de inicio de 1955 + 55 años es el año final de 2010, en el que se aplica el ingreso equivalente de $24,427.87.
Notas Importantes
Tu Calculadora BAII Plus
Los botones de valor de dinero en tiempo están diseñados para cálculos financieros y requieren que sigas la convención de cash flo w sign en todo momento. Recuerda que esta convención requiere que el dinero que te deje ser ingresado como número negativo, y que el dinero que estés recibiendo por ti sea ingresado como un número positivo.
Cuando se adapta esta función a cálculos económicos como la inflación, no se invierte ni se recibe dinero; los números se mueven a través del tiempo. Para obedecer el requisito de la calculadora de la convención de signos de flujo de efectivo, asegúrese de que los signos adjuntos a los valores presentes (\(PV\)) y futuros (\(FV\)) sean opuestos. La elección de cuál es positiva y cuál es negativa es arbitraria y no afecta el resultado del cálculo. Ignorar el signo de flujo de caja que se muestra en cualquier solución
Muchos expertos afirman hoy que el jubilado canadiense promedio en 2012 necesita aproximadamente 40,000 dólares en ingresos brutos anuales para jubilarse cómodamente. Supongamos que tienes 20 años en 2012. Históricamente en Canadá, la tasa de inflación ha promediado 3.16%. Si la tasa promedio de inflación continúa en el futuro, ¿qué ingreso bruto requerirá cuando se jubile a los 65 años?
Solución
Calcula el valor final (\(FV\)) para tus ingresos brutos anuales cuando te jubilas a los 65 años.
Lo que ya sabes
Paso 1:
Se conocen el valor actual, la tasa de inflación fija y el período de tiempo, como se ilustra en la línea de tiempo.
Años = 45

Cómo Llegarás
Paso 2:
Con a\(CY\) = 1, la\(i = IY\).
Paso 3:
Aplicar la Fórmula 9.2 para calcular el número de periodos compuestos.
Paso 4:
Calcular el valor futuro aplicando la Fórmula 9.3.
Realizar
Paso 2:
\(i\)= 3.16%
Paso 3:
\(N\)= 1 × 45 = 45
Paso 4:
\(FV = \$40,000(1 + 0.0316)^{45} = \$162,207.15\)
| N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|
| 45 | 3.16 | -40000 | 0 | Respuesta: 160,798.0247 | 1 | 1 |
Cuando te jubilas en 2057, si la inflación continúa promediando 3.16% anual, según los expertos tu ingreso bruto anual debe ser de $162,207.15 para que vivas cómodamente.
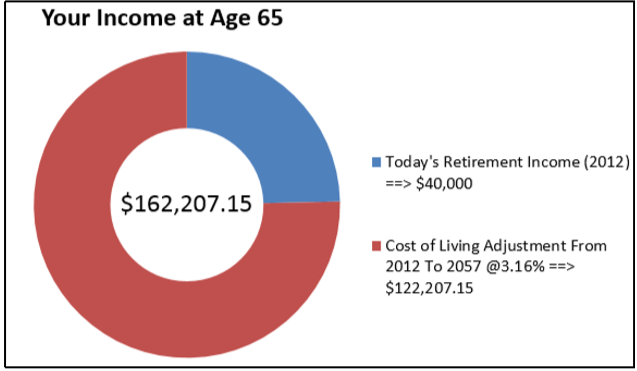
Instrucciones de Excel
Abra la plantilla de Excel titulada “Capítulo 9: Plantilla de Pagos Únicos e Intereses Compuestos”.

Poder adquisitivo
Recordemos de la sección 4.3 que el poder adquisitivo de un dólar es la cantidad de bienes y servicios que se pueden intercambiar por un dólar. El poder adquisitivo tiene una relación inversa con la inflación. Cuando ocurre la inflación y los precios aumentan, tu poder adquisitivo disminuye.
La Fórmula
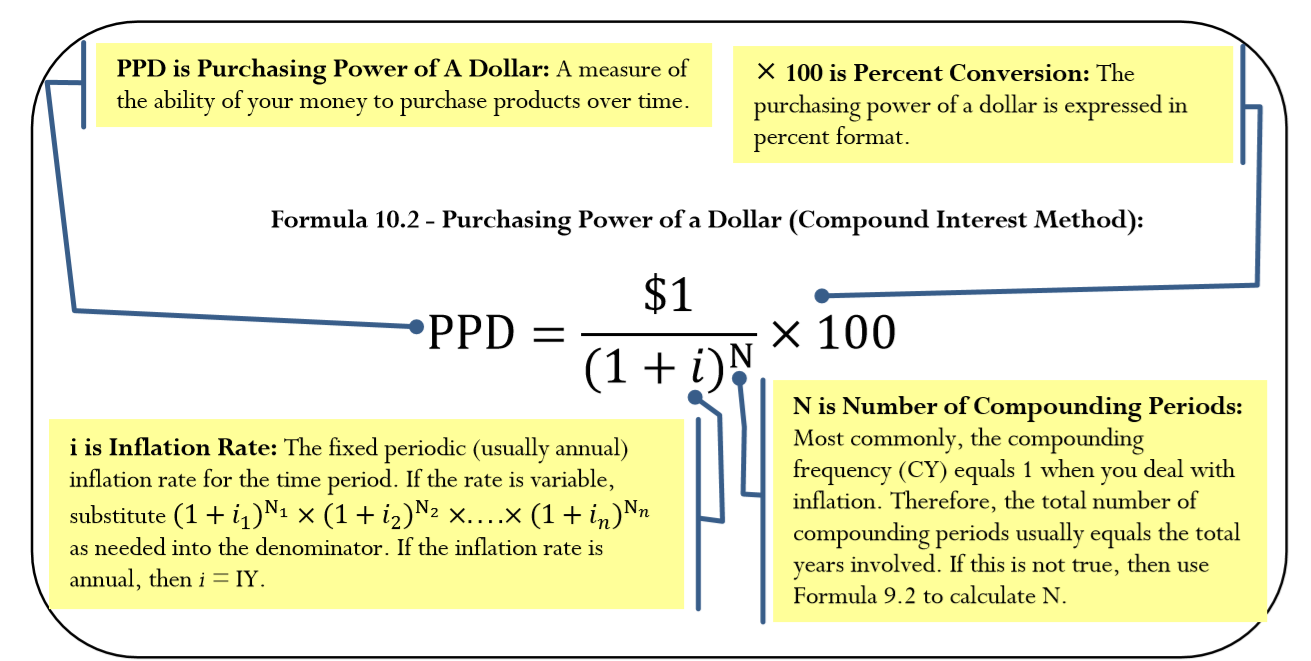
En la fórmula introducida en la sección 4.3, el denominador utilizó el IPC para representar el cambio en los precios de los productos. En las aplicaciones de interés compuesto, en su lugar se utiliza la tasa de inflación, como se muestra en la Fórmula 10.2.
Cómo funciona
Siga estos pasos para resolver una pregunta de poder adquisitivo usando interés compuesto:
Paso 1: Identificar la tasa de inflación (\(IY\)), la capitalización sobre la tasa de inflación (\(CY\)), y el término (Años). Normalmente,\(i = IY\) y\(N\) = Años; sin embargo, aplicar la Fórmula 9.1 y la Fórmula 9.2 si es necesario calcular\(i\) o\(N\).
Paso 2: Aplicar la Fórmula 10.2, resolviendo por el poder adquisitivo de un dólar.
Usando el ejemplo de ingresos, determine cómo ha cambiado el poder adquisitivo de un individuo de 1955 a 2010. Recordemos que la inflación promedio durante el periodo fue de 3.91% anual.
Paso 1: El\(IY\) = 3.91%,\(CY\) = 1, y Años = 55. La tasa anual deja\(i\) = 3.91% y\(N\) = 54.
Paso 2: A partir de la Fórmula 10.2, el\(PPD=\dfrac{\$ 1}{(1+0.0391)^{55}} \times 100=12.1296 \%\). Como interpretación aproximada, esto significa que si alguien pudiera comprar 100 artículos con $100 en 1955, esos mismos $100 solo comprarían alrededor de 12 de los mismos artículos en 2010.
Cosas a tener en cuenta
Determina exactamente cuál es la pregunta que te está pidiendo calcular con respecto al poder adquisitivo de un dólar.
- Si la pregunta pregunta: “¿Cuál es el poder adquisitivo de un dólar?” entonces tu respuesta es el resultado de la Fórmula 10.2.
- Si las preguntas se preguntan, “¿Cómo ha disminuido su poder adquisitivo?” entonces tu respuesta es 100% menos el resultado de la Fórmula 10.2.
Es fundamental Planear a la hora de resolver estas preguntas para que su solución aborde la pregunta planteada.
Cuál es el poder adquisitivo de tu dólar si los precios de los productos:
- ¿Doble?
- ¿Triple?
- ¿Cuádruple?
- Contestar
-
- 1/2 = 50%
- 1/3 =\(3.3\bar{3}\%\)
- 1/4 = 25%
Las tasas históricas de inflación en Canadá fueron de 3.13% de junio de 2007 a junio de 2008, − 0.26% de junio de 2008 a junio de 2009, y 0.96% de junio de 2009 a junio de 2010. Comparando junio de 2007 con junio de 2010, ¿cuál es el poder adquisitivo de un dólar de 2007 en 2010?
Solución
Calcular el poder adquisitivo de un dólar 2007 (\(PPD\)) en 2010.
Lo que ya sabes
Paso 1:
Se conocen las tasas y términos de inflación, como se ilustra en la línea de tiempo.
\(CY\)(para cada segmento de tiempo) = 1, Plazo (para cada segmento de tiempo) = 1 Año

Cómo Llegarás
Paso 1 (continuación):
Identificar la tasa de interés periódica (\(i\)) y el número de compuestos (\(N\)) para cada segmento de tiempo. Con\(CY\) = 1, entonces\(i = IY\) y\(N\) = Años.
Paso 2:
Aplicar la Fórmula 10.2, sustituyendo la versión de tasa de interés variable en el denominador.
Realizar
Paso 1 (continuación):
\(i_1\)= 3.13%,\(i_2\) = − 0.26%,\(i_3\) = 0.96%;\(N_1, N_2, N_3\) = 1
Paso 2:
\ [\ begin {alineado}
PPD &=\ dfrac {\ $1} {(1+0.0313)\ times (1-0.0026)\ times (1+0.0096)}\ times 100\\
&=96.2933\%
\ end {alineado}\ nonumber\]
Instrucciones de la calculadora
| Segmento de tiempo | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 3.13 | Respuesta: 0,969649 | 0 | -1 | 1 | 1 |
| 2 | \(\surd\) | -0.26 | Respuesta: 0,972177 | \(\surd\) | -0.969649 | \(\surd\) | \(\surd\) |
| 3 | \(\surd\) | 0.96 | Respuesta: 0,962933 | \(\surd\) | -0.972177 | \(\surd\) | \(\surd\) |
El poder adquisitivo de un dólar de junio de 2007 en junio de 2010 es de 96.2933%. Si $100 en junio de 2007 pudieran comprar 100 artículos, en junio de 2010 $100 solo podrían comprar alrededor de 96 artículos.
Tasas de Cambio
Recuerda de la sección 3.1 que podrías calcular un cambio porcentual entre números Antiguos y Nuevos. Si bien esta fórmula funciona bien cuando estás interesado en un solo porcentaje de cambio, se vuelve laborioso y tedioso cuando trabajas con una serie de cambios porcentuales. Por ejemplo, supongamos que el\(TSX\) tiene un valor de 12,000. El\(TSX\) entonces baja 4% cada mes durante cinco meses, y luego sube 4% cada mes durante cinco meses. ¿Cuál es el valor “Nuevo” para el\(TSX\)? ¡No son 12 mil! Si usa la fórmula para el cambio porcentual, necesita una serie de 10 cálculos que resuelvan para “Nuevo” cada vez, ¡un cálculo por cada mes! No es muy divertido. Matemáticamente, en una serie de cambios porcentuales, cada cambio se compone del anterior. Por lo tanto, puede utilizar fórmulas de interés compuesto para trabajar con cualquier serie de cambios porcentuales.
La Fórmula
Puede resolver cualquier serie de cambios porcentuales aplicando una versión adaptada de Fórmula 9.3 para las tasas de interés variables:

Cómo funciona
Siga estos pasos para adaptar la Fórmula 9.3 para aplicaciones de cambio porcentual:
Paso 1: Asigne el valor “Antiguo” a\(PV\) o el valor “Nuevo” a\(FV\) (dependiendo de cuál conozca).
Paso 2: Identifique su serie de cambios porcentuales (\(i_1\)a través\(i_n\)) y cuántas veces seguidas se produce cada valor porcentual de cambio (\(N_1\)a través\(N_n\)). Recuerda que las disminuciones son valores negativos.
Paso 3: Aplicar la versión adaptada de Fórmula 9.3, resolviendo para cualquiera\(FV\) o\(PV\).
A modo de ejemplo, averigua el nuevo valor para el\(TSX\) basado en un valor inicial de 12,000 con disminuciones de 4% durante cinco meses seguido de incrementos de 4% durante cinco meses.
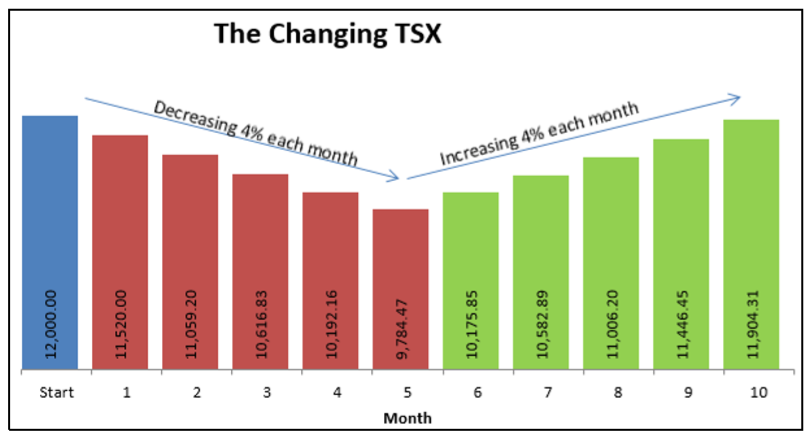
Paso 1: El valor “Viejo” es\(PV\) =12,000.
Paso 2: El primer cambio es una disminución de 4%, o\(i_1\) = − 4%. Ocurre por cinco meses seguidos, por lo tanto\(N_1\) = 5. A continuación, un incremento de 4%, o\(i_2\) = 4%, también ocurre cinco meses seguidos, por lo tanto\(N_2\) = 5.
Paso 3: Usa la Fórmula 9.3 para calcular\(FV = 12,000 × (1 − 0.04)^5 × (1 + 0.04)^5 = 11,904.31\). El valor “Nuevo” del\(TSX\) después de los 10 meses de cambio es de 11,904.31.
Notas Importantes
Puedes usar tu calculadora financiera f o estos cálculos no financieros tal como lo hiciste para la inflación. Debes seguir la convención de señales de flujo de caja asegurándote de eso\(PV\) y\(FV\) tener signos opuestos. No obstante, una vez más los signos no tienen ningún significado en estos cálculos.
Cosas a tener en cuenta
Cuando trabajas con tasas de inflación variables, poder adquisitivo de un dólar o tasas de cambio, puedes simplificar las tasas variables en una sola tasa fija usando un promedio geométrico antes de aplicar la fórmula de interés compuesto. Por ejemplo, usando el\(TSX\) ejemplo anterior, el promedio geométrico de los 10 meses de cambio es:
\[GAvg =\left [\sqrt[10]{(1-0.04)^{5} \times(1+0.04)^{5}}-1 \right] \times 100=-0.080032 \% \nonumber \]
Utilizando este valor calculado como tasa de interés periódica y sustituyendo a la Fórmula 9.3 se produce:
\[FV = 12,000 × (1 − 0.00080032)^{10} = 11,904.31\nonumber \]
De igual manera, se podría resolver Ejemplo\(\PageIndex{2}\) con este enfoque. Algunos estudiantes han encontrado esta técnica más fácil que trabajar con las tasas variables. De cualquier manera, ya sea que use tasas variables o el promedio geométrico como tasa fija, ambas técnicas producen la misma solución.
Si una cantidad disminuye\(x\%\) y luego aumenta en el mismo porcentaje, ¿por qué no llegas a la cantidad original como tu valor “Nuevo”?
- Contestar
-
La disminución inicial hará que el número base sea menor. Si el nuevo número de base se incrementa entonces en el mismo porcentaje, ese porcentaje se determina a partir de una base menor. No producirá el mismo valor que la disminución.
La ciudad de Vancouver rastrea el empleo en su área Metro Core. En 1971, aproximadamente 45 mil empleados del área Metro Core fueron clasificados como trabajadores de “servicio profesional y comercial”. De 1971 a 1981, el número de trabajadores creció alrededor de 4.5% anual. De 1981 a 1991, la tasa de crecimiento fue de alrededor de 3.1% anual, y de 1991 a 2001 la tasa de crecimiento fue de aproximadamente 1.5% por año.4 Redondeado al mil más cercano, ¿cuántas personas estaban empleadas en el campo “servicios profesionales y comerciales” en el área Metro Core de Vancouver en 2001?
Solución
Se busca el valor “Nuevo” (\(FV\)) del número de empleados después de los 30 años de cambios porcentuales.
Lo que ya sabes
Paso 1:
Se conoce el valor inicial y la estructura de la secuencia de cambios porcentuales, como se muestra en la línea de tiempo.
Cómo Llegarás
Paso 2:
Capturar los valores de\(i_n\) y\(N_n\) para cada valor de cambio porcentual consecutivo. Tenga en cuenta que la línea de tiempo tiene tres segmentos de tiempo, por lo que cada variable tiene tres valores.
Paso 3:
Aplicar Fórmula 9.3.

Realizar
Paso 2:
\[i_{1}=4.5 \%, N_{1}=10, i_{2}=3.1 \%, N_{2}=10, i_{3}=1.5 \%, N_{3}=10 \nonumber \]
Paso 3:
\ [\ begin {aligned}
&FV=45,000\ times (1+0.045) ^ {10}\ times (1+0.031) ^ {10}\ times (1+0.015) ^ {10}\
&FV=45.000\ times 1.045^ {10}\ times 1.031^ {10}\ times 1.015^ {10}\
&FV=45.000\ times 1.552969\ times 1.357021\ times 1.160540=110,058=110,000
\ end { alineado}\ nonumber\]
Instrucciones de la calculadora
| Segmento de tiempo | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| 1 | 10 | 4.5 | -45000 | 0 | Respuesta: 69,883,62398 | 1 | 1 |
| 2 | \(\surd\) | 3.1 | -69,883.62398 | \(\surd\) | Respuesta: 94,833,56372 | \(\surd\) | \(\surd\) |
| 3 | \(\surd\) | 1.5 | -94,833.56372 | \(\surd\) | Respuesta: 110,058.2223 | \(\surd\) | \(\surd\) |
De 1971 a 2001, el número de empleados en el campo de los “servicios profesionales y comerciales” en el área Metro Core de Vancouver creció de 45,000 a 110.000.
Referencias
- Statistics Canada, “Promedio anual, semanal y por hora, asalariados masculinos y femeninos, Industrias manufactureras, Canadá, 1934 a 1969”, adaptado de la Serie E60—68, www.statcan.gc.ca/pub/11-516-x/ sectione/E60 _68eng.csv, consultado el 28 de julio de 2010.
- Statistics Canada, “Ganancias, Semanal Promedio, por Provincia y Territorio”, adaptado de la tabla CANSIM 281-0027 y Catalogue no. 72-002-X, www40.statcan.gc.ca/ l01/cst01 /labr79-eng.htm, consultado el 11 de agosto de 2011.
- Statistics Canada, “Consumer Price Indexes for Canada, Monthly, 1914—2012 (V41690973 Series)”; todos los valores basados en mayo de cada año; www.bankofcanada.ca/rates/related/inflation-calculator/? page_moved=1, consultado el 26 de noviembre de 2012.
- Ciudad de Vancouver, “Employment Change in the Metro Core”, 22 de noviembre de 2005, http://s3.amazonaws.com/zanran_stora...es/7116122.pdf, consultado el 20 de agosto de 2013


