3.1: Aplicaciones de maximización
- Page ID
- 113909
En esta sección, aprenderás a:
- Reconocer la forma típica de un problema de programación lineal
- Formular problemas de programación lineal de maximización
- Gráfico de regiones de viabilidad para problemas de programación lineal de maximización
- Determinar soluciones óptimas para problemas de programación lineal de maximización.
Los problemas de aplicación en los negocios, la economía y las ciencias sociales y de la vida a menudo nos piden tomar decisiones sobre la base de ciertas condiciones. Las condiciones o limitaciones a menudo toman la forma de desigualdades. En esta sección, comenzaremos a formular, analizar y resolver tales problemas, a un nivel simple, para comprender los muchos componentes de dicho problema.
Un problema típico de programación lineal consiste en encontrar un valor extremo de una función lineal sujeta a ciertas restricciones. Estamos tratando de maximizar o minimizar el valor de esta función lineal, como maximizar las ganancias o ingresos, o minimizar el costo. Es por ello que estos problemas de programación lineal se clasifican como problemas de maximización o minimización, o simplemente problemas de optimización. La función que estamos tratando de optimizar se llama función objetiva, y las condiciones que deben satisfacerse se llaman restricciones.
Un ejemplo típico es maximizar el beneficio de producir varios productos, sujeto a limitaciones en los materiales o recursos necesarios para producir estos artículos; el problema requiere que determinemos la cantidad de cada artículo producido. Otro tipo de problema implica la programación; necesitamos determinar cuánto tiempo dedicar a cada una de las diversas actividades para maximizar los ingresos de (o minimizar el costo de) estas actividades, sujeto a limitaciones de tiempo y otros recursos disponibles para cada actividad.
En este capítulo, trabajaremos con problemas que involucran sólo dos variables, y por lo tanto, se pueden resolver graficando. En el siguiente capítulo, aprenderemos un algoritmo para encontrar una solución numéricamente. Eso nos proporcionará una herramienta para resolver problemas con más de dos variables. En ese momento, con un poco más de conocimiento sobre programación lineal, también exploraremos las muchas formas en que estas técnicas se utilizan en los negocios y una amplia variedad de otros campos.
Comenzamos resolviendo un problema de maximización.
Niki tiene dos empleos de medio tiempo, Job I y Job II. Ella nunca quiere trabajar más de un total de 12 horas a la semana. Ella ha determinado que por cada hora que trabaja en el Trabajo I, necesita 2 horas de tiempo de preparación, y por cada hora que trabaja en el Job II, necesita una hora de tiempo de preparación, y no puede gastar más de 16 horas en preparación.
Si Nikki gana $40 la hora en el Trabajo I, y $30 la hora en el Trabajo II, ¿cuántas horas debería trabajar a la semana en cada trabajo para maximizar sus ingresos?
Solución
Comenzamos por elegir nuestras variables.
- Let\(x\) = El número de horas semanales Niki trabajará en el Job I.
- Let\(y\) = El número de horas semanales Niki trabajará en el Job II.
Ahora escribimos la función objetiva. Dado que a Niki se le pagan 40 dólares la hora en el Trabajo I, y 30 dólares la hora en el Trabajo II, su ingreso total I viene dado por la siguiente ecuación.
\[I = 40x + 30y \nonumber \]
Nuestra siguiente tarea es encontrar las limitaciones. La segunda frase del problema dice: “Ella nunca quiere trabajar más de un total de 12 horas semanales”. Esto se traduce en la siguiente restricción:
\[x + y \leq 12 \nonumber \]
La tercera frase dice: “Por cada hora que trabaja en el Trabajo I, necesita 2 horas de tiempo de preparación, y por cada hora que trabaja en el Job II, necesita una hora de tiempo de preparación, y no puede dedicar más de 16 horas para la preparación”. A continuación se presenta la traducción.
\[2x + y \leq 16 \nonumber \]
El hecho de que\(x\) y nunca\(y\) pueda ser negativo está representado por las dos limitaciones siguientes:
\[x \geq 0 \text{, and } y \geq 0 \nonumber. \nonumber \]
Bueno, ¡buenas noticias! Nosotros hemos formulado el problema. Lo reafirmamos como
\ begin {array} {ll}
\ textbf {Maximizar} &\ mathrm {I} =40\ mathrm {x} +30\ mathrm {y}\
\\ textbf {Sujeto a:} &\ mathrm {x} +\ mathrm {y}\ leq 12\\
& 2\ mathrm {x} +\ mathrm {y}\ leq 16\
&\ mathrm {x}\ geq 0;\ mathrm {y}\ geq 0
\ fin {matriz}
Para resolver el problema, graficamos las restricciones y sombreamos la región que satisface todas las restricciones de desigualdad.
Se puede utilizar cualquier método apropiado para graficar las líneas de las restricciones. Sin embargo, a menudo el método más fácil es graficar la línea trazando la intercepción x y.
La línea para una restricción dividirá el plano en dos regiones, una de las cuales satisface la parte de desigualdad de la restricción. Se utiliza un punto de prueba para determinar qué porción del plano sombrear para satisfacer la desigualdad. Cualquier punto en el plano que no esté en la línea se puede utilizar como punto de prueba.
- Si el punto de prueba satisface la desigualdad, entonces la región del plano que satisface la desigualdad es la región que contiene el punto de prueba.
- Si el punto de prueba no satisface la desigualdad, entonces la región que satisface la desigualdad se encuentra en el lado opuesto de la línea desde el punto de prueba.
En la gráfica siguiente, después de graficar las líneas que representan las restricciones utilizando un método apropiado del Capítulo 1, se utilizó el punto (0,0) como punto de prueba para determinar que
- (0,0) satisface la restricción\(x + y \leq 12\) porque\(0 + 0 < 12\)
- (0,0) satisface la restricción\(2x + y \leq 16\) porque\(2(0) + 0 < 16\)
Por lo tanto, en este ejemplo, sombreamos la región que está por debajo y a la izquierda de ambas líneas de restricción, pero también por encima del eje x y a la derecha del eje y, con el fin de satisfacer aún más las restricciones\(x \geq 0\) y\(y \geq 0\).
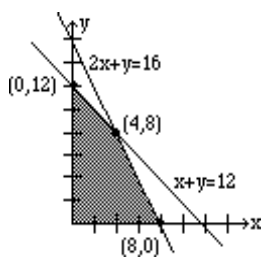
La región sombreada donde se cumplen todas las condiciones se denomina región de factibilidad o polígono de factibilidad.
El Teorema Fundamental de la Programación Lineal establece que el valor máximo (o mínimo) de la función objetiva siempre tiene lugar en los vértices de la región de factibilidad.
Por lo tanto, identificaremos todos los vértices (puntos de esquina) de la región de factibilidad. A estos puntos los llamamos puntos críticos. Se listan como (0, 0), (0, 12), (4, 8), (8, 0). Para maximizar los ingresos de Niki, sustituiremos estos puntos en la función objetiva para ver qué punto nos da el mayor ingreso por semana. A continuación enumeramos los resultados.
| Puntos Críticos | Ingresos |
|---|---|
| (0, 0) | 40 (0) + 30 (0) = $0 |
| (0, 12) | 40 (0) + 30 (12) = $360 |
| (4, 8) | 40 (4) + 30 (8) = $400 |
| (8, 0) | 40 (8) + 30 (0) = $320 |
Claramente, el punto (4, 8) da la mayor ganancia: 400 dólares.
Por lo tanto, concluimos que Niki debería trabajar 4 horas en el Job I, y 8 horas en el Job II.
Una fábrica fabrica dos tipos de gadgets, regulares y premium. Cada gadget requiere el uso de dos operaciones, montaje y acabado, y hay como máximo 12 horas disponibles para cada operación. Un gadget normal requiere 1 hora de montaje y 2 horas de acabado, mientras que un gadget premium necesita 2 horas de ensamblaje y 1 hora de acabado. Debido a otras restricciones, la compañía puede fabricar como máximo 7 gadgets al día. Si se obtiene una ganancia de $20 por cada gadget regular y $30 por un gadget premium, ¿cuántos de cada uno deben fabricarse para maximizar las ganancias?
Solución
Elegimos nuestras variables.
- Let\(x\) = El número de gadgets regulares fabricados cada día.
- y\(y\) = El número de gadgets premium fabricados cada día.
La función objetiva es
\[P = 20x + 30y \nonumber \]
Ahora escribimos las restricciones. En la cuarta frase se establece que la empresa puede fabricar como máximo 7 gadgets al día. Esto se traduce como
\[x + y \leq 7 \nonumber \]
Dado que el gadget regular requiere una hora de montaje y el gadget premium requiere dos horas de ensamblaje, y hay como máximo 12 horas disponibles para esta operación, obtenemos
\[x + 2y \leq 12 \nonumber \]
De igual manera, el gadget regular requiere dos horas de acabado y el gadget premium una hora. De nuevo, hay como máximo 12 horas disponibles para el acabado. Esto nos da la siguiente restricción.
\[2x + y \leq 12 \nonumber \]
El hecho de que\(x\) y nunca\(y\) pueda ser negativo está representado por las dos limitaciones siguientes:
\[x \geq 0 \text{, and } y \geq 0 \nonumber. \nonumber \]
Hemos formulado el problema de la siguiente manera:
\ [\ begin {array} {ll}
\ textbf {Maximizar} &\ mathrm {P} =20\ mathrm {x} +30\ mathrm {y}\\\ textbf {Sujeto a:} &
\ mathrm {x} +\ mathrm {y}\ leq 7\ &\ mathrm {x} +2\ mathrm {y}\ leq 12\\
& 2\ mathrm {x} +2\ mathrm {y}\ leq 12\\
& 2\ mathrm {x} {x} +\ mathrm {y}\ leq 12\\
&\ mathrm {x}\ geq 0;\ mathrm {y}\ geq 0
\ end {array}\ nonumber\]
Para resolver el problema, a continuación graficamos las restricciones y la región de factibilidad.
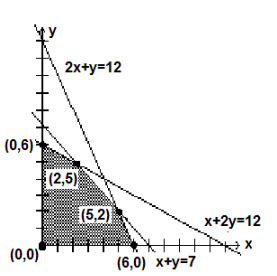
Nuevamente, hemos sombreado la región de factibilidad, donde se satisfacen todas las limitaciones.
Dado que el valor extremo de la función objetiva siempre tiene lugar en los vértices de la región de factibilidad, identificamos todos los puntos críticos. Se listan como (0, 0), (0, 6), (2, 5), (5, 2) y (6, 0). Para maximizar el beneficio, sustituiremos estos puntos en la función objetiva para ver qué punto nos da el máximo beneficio cada día. Los resultados se enumeran a continuación.
| Punto Crítico | Ingresos |
|---|---|
| (0, 0) | 20 (0) + 30 (0) = $0 |
(0, 6) |
20 (0) + 30 (6) = $180 |
(2, 5) |
20 (2) + 30 (5) = $190 |
(5, 2) |
20 (5) + 30 (2) = $160 |
| (6,0) | 20 (6) + 30 (0) = $120 |
El punto (2, 5) da la mayor ganancia, y esa ganancia es de 190 dólares.
Por lo tanto, concluimos que debemos fabricar 2 gadgets regulares y 5 gadgets premium diarios para obtener el beneficio máximo de $190.
Hasta el momento nos hemos centrado en “problemas de maximización estándar” en los que
- La función objetiva es ser maximizada
- Todas las restricciones son de la forma\(ax + by \leq c\)
- Todas las variables están restringidas por no negativas (\(x ≥ 0\),\(y ≥ 0\))
A continuación consideraremos un ejemplo donde ese no es el caso. Se dice que nuestro siguiente problema tiene “restricciones mixtas”, ya que algunas de las restricciones de desigualdad son de la forma\(ax + by ≤ c\) y otras son de la forma\(ax + by ≥ c\). Las restricciones de no negatividad siguen siendo un requisito importante en cualquier programa lineal.
Resolver gráficamente el siguiente problema de maximización.
\ [\ begin {array} {ll}
\ textbf {Maximizar} &\ mathrm {P} =10\ mathrm {x} +15\ mathrm {y}\
\\ textbf {Sujeto a:} &\ mathrm {x} +\ mathrm {y}\ geq 1\\
&\ mathrm {x} +2\ mathrm {y}\ leq 6\
& 2\ mathrm {x} +\ mathrm {y}\ leq 6\\
&\ mathrm {x}\ geq 0;\ mathrm {y}\ geq 0
\ end {array}\ nonumber\]
Solución
A continuación se muestra la gráfica.
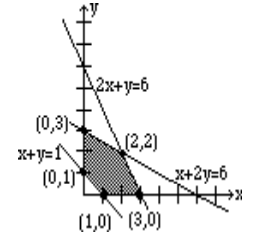
Los cinco puntos críticos se enumeran en la figura anterior. El lector debe observar que la primera restricción\(x + y ≥ 1\) requiere que la región de factibilidad esté delimitada por debajo por la línea\(x + y =1\); el punto de prueba (0,0) no satisface\(x + y ≥ 1\), por lo que sombreamos la región en el lado opuesto de la línea desde el punto de prueba (0,0).
| Punto crítico | Ingresos |
|---|---|
| (1, 0) | 10 (1) + 15 (0) = $10 |
| (3, 0) | 10 (3) + 15 (0) = $30 |
| (2, 2) | 10 (2) + 15 (2) = $50 |
| (0, 3) | 10 (0) + 15 (3) = $45 |
| (0,1) | 10 (0) + 15 (1) = $15 |
Claramente, el punto (2, 2) maximiza la función objetiva a un valor máximo de 50.
Es importante observar que si el punto (0,0) se encuentra en la línea para una restricción, entonces (0,0) no podría usarse como punto de prueba. Tendríamos que seleccionar cualquier otro punto que queramos que no se encuentre en la línea para usarlo como punto de prueba en esa situación.
Por último, abordamos una cuestión importante. ¿Es posible determinar el punto que da el valor máximo sin calcular el valor en cada punto crítico?
La respuesta es sí.
Por ejemplo\(\PageIndex{2}\), sustituimos los puntos (0, 0), (0, 6), (2, 5), (5, 2) y (6, 0), en la función objetiva\(P = 20x + 30y\), y obtuvimos los valores $0, $180, $190, $160, $120, respectivamente.
A veces esa no es la forma más eficiente de encontrar la solución óptima. En su lugar, podríamos encontrar el valor óptimo graficando también la función objetiva.
Para determinar el más grande\(P\), graficamos\(P = 20x + 30y\) para cualquier valor\(P\) de nuestra elección. Digamos, elegimos\(P = 60\). Nosotros graficamos\(20x + 30y = 60\).
Ahora movemos la línea paralela a sí misma, es decir, manteniendo la misma pendiente en todo momento. Ya que estamos moviendo la línea paralela a sí misma, la pendiente se mantiene igual, y lo único que está cambiando es la P. A medida que nos alejamos del origen, el valor de P aumenta. El mayor valor posible de P se realiza cuando la línea toca el último punto de esquina de la región de factibilidad.
La siguiente figura muestra los movimientos de la línea, y la solución óptima se logra en el punto (2, 5). En problemas de maximización, a medida que la línea se aleja del origen, este punto óptimo es el punto crítico más lejano.
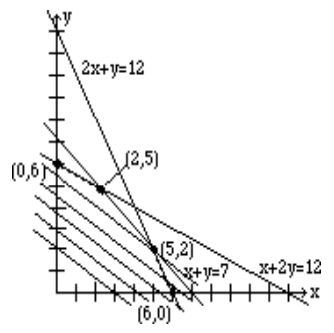
Resumimos:
Los problemas de programación lineal de maximización
- Escribe la función objetiva.
- Escribe las restricciones.
- Para los problemas de programación lineal de maximización estándar, las restricciones son de la forma:\(ax + by ≤ c\)
- Como las variables no son negativas, incluimos las restricciones:\(x ≥ 0\);\(y ≥ 0\).
- Grafica las restricciones.
- Sombra la región de factibilidad.
- Encuentra los puntos de esquina.
- Determinar el punto de esquina que da el valor máximo.
- Esto se hace encontrando el valor de la función objetiva en cada punto de esquina.
- Esto también se puede hacer moviendo la línea asociada a la función objetiva.


