5.5: Gráficas y propiedades de las funciones logarítmicas

Última actualización
Guardar como PDF

Page ID: 113693

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

En esta sección, usted:

examinar las propiedades de las funciones logarítmicas
examinar gráficos de funciones logarítmicas
examinar la relación entre gráficas de funciones exponenciales y logarítmicas

Recordemos que la función exponencial$f(x) = 2^x$ produce esta tabla de valores

$x$	-3	-2	-1	0	1	2	3
$f(x)$	1/8	1/4	1/2	1	2	4	8

Dado que la función logarítmica es una inversa de la exponencial,$g(x)=\log_{2}(x)$ produce la tabla de valores

$x$	1/8	1/4	1/2	1	2	4	8
$g(x)$	-3	-2	-1	0	1	2	3

En esta segunda tabla, fíjese que

A medida que aumenta la entrada, la salida aumenta.
A medida que aumenta la entrada, la salida aumenta más lentamente.
Dado que la función exponencial solo genera valores positivos, el logaritmo solo puede aceptar valores positivos como entradas, por lo que el dominio de la función log es$(0, \infty)$.
Dado que la función exponencial puede aceptar todos los números reales como entradas, el logaritmo puede tener cualquier número real como salida, por lo que el rango es todos los números reales o$(-\infty, \infty)$.

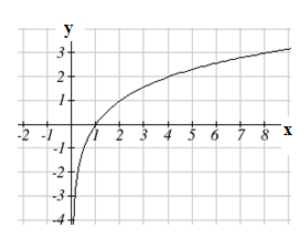
$5.5.png$

Trazando la gráfica de$g(x) = \log_{2}(x)$ desde los puntos de la tabla, observe que a medida que los valores de entrada para$x$ acercarse a cero, la salida de la función crece muy grande en la dirección negativa, lo que indica una asíntota vertical en$x = 0$.

En notación simbólica escribimos

como$x \rightarrow 0^{+}$,$f(x) \rightarrow-\infty$

y como$x \rightarrow \infty, f(x) \rightarrow \infty$

Fuente: El material de esta sección del libro de texto proviene de David Lippman y Melonie Rasmussen, Librería de texto abierto, Precálculo: Una investigación de funciones, “Capítulo 4: Funciones exponenciales y logarítmicas”, licenciado bajo licencia Creative Commons CC BY-SA 3.0. El material aquí se basa en material contenido en ese libro de texto pero ha sido modificado por Roberta Bloom, según lo permitido bajo esta licencia.

Gráficamente, en la función$g(x) = \log_{b}(x)$$b > 1$,, observamos las siguientes propiedades:

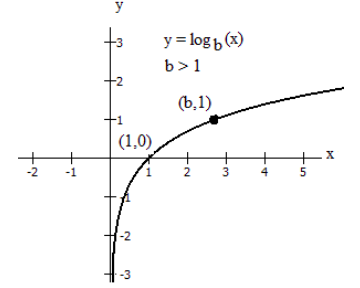
$5.5b.png$

La gráfica tiene una intercepción horizontal en (1, 0)
La línea x = 0 (el eje y) es una asíntota vertical; como$x \rightarrow 0^{+}, y \rightarrow-\infty$
La gráfica va en aumento si$b > 1$
El dominio de la función es$x > 0$, o (0,$\infty$)
El rango de la función es todos los números reales, o$(-\infty, \infty)$

Sin embargo, si la base$b$ es menor que 1, 0$b$ < < 1, entonces la gráfica aparece como abajo.
Esto se deduce de la propiedad log de bases recíprocas:$\log _{1 / b} C=-\log _{b}(C)$

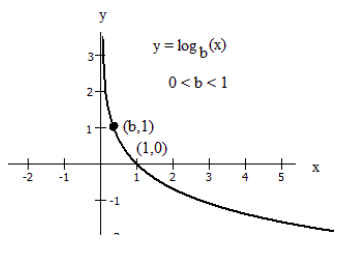
$5.5c.png$

La gráfica tiene una intercepción horizontal en (1, 0)
La línea x = 0 (el eje y) es una asíntota vertical; como$x \rightarrow 0^{+}, y \rightarrow \infty$
La gráfica es decreciente si 0 <$b$ < 1
El dominio de la función es$x$ > 0, o (0,$\infty$)
El rango de la función es todos los números reales, o$(-\infty, \infty)$

Al graficar una función logarítmica, puede ser útil recordar que la gráfica pasará por los puntos (1, 0) y ($b$, 1).

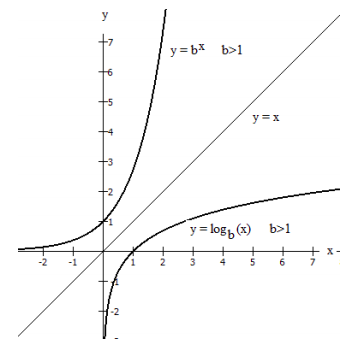
Finalmente, comparamos las gráficas de$y = b^x$ y$y = \log_{b}(x)$, que se muestran a continuación en los mismos ejes.

Debido a que las funciones son funciones inversas entre sí, para cada par ordenado específico
($h$,$k$) en la gráfica de$y = b^x$, encontramos el punto ($k$,$h$) con las coordenadas invertidas en la gráfica de$y = \log_{b}(x)$.

En otras palabras, si el punto con$x = h$ y$y = k$ está en la gráfica de$y = b^x$, entonces el punto con$x = k$ y$y = h$ se encuentra en la gráfica de$y = \log_{b} (x)$

El dominio de$y = b^x$ es el rango de$y = \log_{b} (x)$

El rango de$y = b^x$ es el dominio de$y = \log_{b} (x)$

Por esta razón, las gráficas aparecen como reflejos, o imágenes especulares, entre sí a través de la línea diagonal$y=x$. Esta es una propiedad de las gráficas de funciones inversas que los estudiantes deben recordar de su estudio de las funciones inversas en su clase de álgebra prerrequisito.

$5.5d.png$

	$\bf{y = b^x}$, con$\bf{b>1}$	$\bf{y = \log_{b} (x)}$, con$\bf{b>1}$
Dominio	\ (\ bf {y = b^x}\), con$\bf{b">1}$ "valign="top” width="188" class="lt-math-38599"> todos los números reales	\ (\ bf {y =\ log_ {b} (x)}\), con$\bf{b">1}$ "valign="top” width="189" class="lt-math-38599"> todos los números reales positivos
Rango	\ (\ bf {y = b^x}\), con$\bf{b">1}$ "valign="top” width="188" class="lt-math-38599"> todos los números reales positivos	\ (\ bf {y =\ log_ {b} (x)}\), con$\bf{b">1}$ "valign="top” width="189" class="lt-math-38599"> todos los números reales
Intercepta	\ (\ bf {y = b^x}\), con$\bf{b">1}$ "valign="top” width="188" class="lt-math-38599"> (0,1)	\ (\ bf {y =\ log_ {b} (x)}\), con$\bf{b">1}$ "valign="top” width="189" class="lt-math-38599"> (1,0)
Asíntotas	\ (\ bf {y = b^x}\), con$\bf{b">1}$ "valign="top” width="188" class="lt-math-38599"> La asíntota horizontal es la línea y = 0 (el eje x) Como$x \rightarrow-\infty, \: y \rightarrow 0$	\ (\ bf {y =\ log_ {b} (x)}\), con$\bf{b">1}$ "valign="top” width="189" class="lt-math-38599"> La asíntota vertical es la línea x = 0 (el eje y) Como$x \rightarrow 0^{+}, \: y \rightarrow-\infty$

	\(\bf{y = b^x}\), con\(\bf{b>1}\)	\(\bf{y = \log_{b} (x)}\), con\(\bf{b>1}\)
Dominio	\ (\ bf {y = b^x}\), con\(\bf{b">1}\) "valign="top” width="188" class="lt-math-38599"> todos los números reales	\ (\ bf {y =\ log_ {b} (x)}\), con\(\bf{b">1}\) "valign="top” width="189" class="lt-math-38599"> todos los números reales positivos
Rango	\ (\ bf {y = b^x}\), con\(\bf{b">1}\) "valign="top” width="188" class="lt-math-38599"> todos los números reales positivos	\ (\ bf {y =\ log_ {b} (x)}\), con\(\bf{b">1}\) "valign="top” width="189" class="lt-math-38599"> todos los números reales
Intercepta	\ (\ bf {y = b^x}\), con\(\bf{b">1}\) "valign="top” width="188" class="lt-math-38599"> (0,1)	\ (\ bf {y =\ log_ {b} (x)}\), con\(\bf{b">1}\) "valign="top” width="189" class="lt-math-38599"> (1,0)
Asíntotas	\ (\ bf {y = b^x}\), con\(\bf{b">1}\) "valign="top” width="188" class="lt-math-38599"> La asíntota horizontal es la línea y = 0 (el eje x) Como\(x \rightarrow-\infty, \: y \rightarrow 0\)	\ (\ bf {y =\ log_ {b} (x)}\), con\(\bf{b">1}\) "valign="top” width="189" class="lt-math-38599"> La asíntota vertical es la línea x = 0 (el eje y) Como\(x \rightarrow 0^{+}, \: y \rightarrow-\infty\)