7.1: Juegos y Conteo
- Page ID
- 113636
En esta sección, aprenderás a:
- Usar notación de conjuntos para representar uniones, intersecciones y complementos de conjuntos
- Usa diagramas de Venn para resolver problemas de conteo.
Introducción a los Sets
En esta sección, nos familiarizaremos con las operaciones de conjunto y las notaciones, para que podamos aplicar estos conceptos tanto a problemas de conteo como a problemas de probabilidad. Comenzamos definiendo algunos términos.
Un conjunto es una colección de objetos, y sus miembros se llaman los elementos del conjunto.
Nombramos el conjunto usando letras mayúsculas y encerramos sus miembros entre llaves. Supongamos que necesitamos enumerar a los miembros del club de ajedrez. Utilizamos la siguiente notación de conjunto.
C = {Ken, Bob, Tran, Shanti, Eric}
Un conjunto que no tiene miembros se denomina conjunto vacío. El conjunto vacío se denota con el símbolo\(\varnothing\).
Dos conjuntos son iguales si tienen los mismos elementos.
Set\(A\) es un subconjunto de un conjunto\(B\) si cada miembro de también\(A\) es miembro de\(B\).
Supongamos que C = {Al, Bob, Chris, David, Ed} y A = {Bob, David}. Entonces A es un subconjunto de C, escrito como A\(\subseteq\) C.
Cada conjunto es un subconjunto de sí mismo, y el conjunto vacío es un subconjunto de cada conjunto.
Dejar\(A\) y\(B\) ser dos conjuntos, entonces la unión de\(A\) y\(B\), escrito como\(A \cup B\), es el conjunto de todos los elementos que están ya sea en\(A\) o en\(B\), o en ambos\(A\) y\(B\).
Dejar\(A\) y\(B\0 be two sets, then the intersection of \(A\) y\(B\), escrito como\(A \cap B\), es el conjunto de todos los elementos que son comunes a ambos conjuntos\(A\) y\(B\).
Un conjunto universal\(U\) es el conjunto que consta de todos los elementos bajo consideración.
Dejar\(A\) ser cualquier conjunto, entonces el complemento de conjunto\(A\), escrito como\(\bar{\mathrm{A}}\), es el conjunto que consiste en elementos en el conjunto universal\(U\) que no están en\(A\).
Dos conjuntos A y B se denominan conjuntos disjuntos si su intersección es un conjunto vacío. Claramente, un conjunto y su complemento son disjuntos; sin embargo, dos conjuntos pueden ser disjuntos y no ser complementos.
Enumere todos los subconjuntos del conjunto de colores primarios {rojo, amarillo, azul}.
Solución
Los subconjuntos son\(\varnothing\), {rojo}, {amarillo}, {azul}, {rojo, amarillo}, {rojo, azul}, {amarillo, azul}, {rojo, amarillo, azul}
Tenga en cuenta que el conjunto vacío es un subconjunto de cada conjunto, y un conjunto es un subconjunto de sí mismo.
Vamos F = {Aikman, Jackson, Rice, Sanders, Young}, y vamos B = {Griffey, Jackson, Sanders, Thomas}.
Encuentra la intersección de los conjuntos F y B.
Solución
La intersección de los dos conjuntos es el conjunto cuyos elementos pertenecen a ambos conjuntos. Por lo tanto, F\(\cap\) B = {Jackson, Sanders}
Encuentra la unión de los conjuntos F y B dados de la siguiente manera.
- F = {Aikman, Jackson, Arroz, Lijadoras, Joven}
- B = {Griffey, Jackson, Sanders, Thomas}
Solución
La unión de dos conjuntos es el conjunto cuyos elementos están ya sea en A o en B o en ambos A y B. Observe que al escribir la unión de dos conjuntos, se evitan las repeticiones.
F\(\cup\) B = {Aikman, Griffey, Jackson, Arroz, Sanders, Thomas, Joven}
Deja que el conjunto universal U = {rojo, naranja, amarillo, verde, azul, índigo, violeta}, y P = {rojo, amarillo, azul}. Encuentra el complemento de P.
Solución
El complemento de un conjunto P es el conjunto que consiste en elementos en el conjunto universal U que no están en P. Por lo tanto,
\(\bar{P}\)= {naranja, verde, índigo, violeta}
Para lograr una mejor comprensión, supongamos que el conjunto universal U representa los colores del espectro, y P los colores primarios, luego\(\bar{P}\) representa aquellos colores del espectro que no son colores primarios.
Deja que el conjunto universal U = {rojo, naranja, amarillo, verde, azul, índigo, violeta}, y P = {rojo, amarillo, azul}. Encuentra un conjunto R para que R no sea el complemento de P sino que R y P sean disjuntos.
Solución
R = {naranja, verde} y P = {rojo, amarillo, azul} son disjuntos porque la intersección de los dos conjuntos es el conjunto vacío. Los conjuntos no tienen elementos en común. Sin embargo no son complementos porque su unión P\(\cup\) R = {rojo, amarillo, azul, naranja, verde} no es igual al conjunto universal U.
Dejar U = {rojo, naranja, amarillo, verde, azul, índigo, violeta}, P = {rojo, amarillo, azul}, Q = {rojo, verde}, y R = {naranja, verde, índigo}. Encuentra\(\overline{P \cup Q} \cap \overline{R}\).
Solución
Hacemos los problemas en pasos:
P\(\cup\) Q = {rojo, amarillo, azul, verde}
\(\overline{P \cup Q}\) = {naranja, índigo, violeta}
\(\overline{R}\) = {rojo, amarillo, azul, violeta}
\(\overline{P \cup Q} \cap \overline{R}\) = {violeta}
Diagramas de Venn
Ahora usamos diagramas de Venn para ilustrar las relaciones entre conjuntos. A finales del siglo XIX, un lógico inglés llamado John Venn desarrolló un método para representar la relación entre conjuntos. Él representó estas relaciones usando diagramas, que ahora se conocen como diagramas de Venn.
Un diagrama de Venn representa un conjunto como el interior de un círculo. A menudo, dos o más círculos están encerrados en un rectángulo donde el rectángulo representa el conjunto universal. Visualizar una intersección o unión de un conjunto es fácil. En esta sección, utilizaremos principalmente diagramas de Venn para ordenar diversas poblaciones y contar objetos.
Supongamos que una encuesta a los entusiastas de los automóviles mostró que durante un cierto período de tiempo, 30 condujeron autos con transmisiones automáticas, 20 condujeron autos con transmisiones estándar y 12 condujeron autos de ambos tipos. Si todos en la encuesta manejaban autos con una de estas transmisiones, ¿cuántas personas participaron en la encuesta?
Solución
Usaremos diagramas de Venn para resolver este problema.
Que el set A represente a aquellos entusiastas de los autos que conducían autos con transmisiones automáticas, y el set S representara a los entusiastas de los autos que conducían los autos con transmisiones estándar. Ahora usamos diagramas de Venn para ordenar la información dada en este problema.
Ya que 12 personas manejaban ambos autos, colocamos el número 12 de la región común a ambos conjuntos.
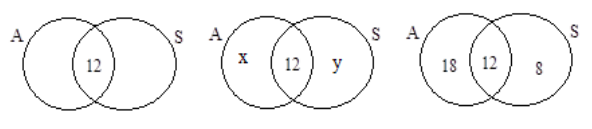
Debido a que 30 personas manejaban autos con transmisiones automáticas, el círculo A debe contener 30 elementos. Esto significa que
x + 12 = 30, o x = 18.
De igual manera, dado que 20 personas manejaban autos con transmisiones estándar, el círculo B debe contener 20 elementos.
Así, y + 12 = 20 que a su vez hace y = 8.
Ahora que toda la información está resuelta, es fácil leer del diagrama que 18 personas manejaban autos con transmisiones automáticas solamente, 12 personas manejaban ambos tipos de autos, y 8 conducían autos con transmisiones estándar solamente.
Por lo tanto, 18 + 12 + 8 = 38 personas participaron en la encuesta.
Una encuesta a 100 personas en California indica que 60 personas han visitado Disneyland, 15 han visitado Knott's Berry Farm y 6 han visitado ambos. ¿Cuántas personas han visitado ninguno de los dos lugares?
Solución
El problema es similar al del ejemplo anterior.
Que el conjunto D represente a las personas que han visitado Disneyland, y K el conjunto de personas que han visitado Knott's Berry Farm.
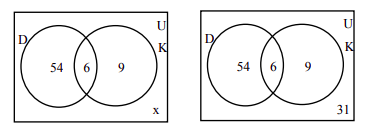
Llenamos las tres regiones asociadas a los conjuntos D y K de la misma manera que antes. Dado que 100 personas participaron en la encuesta, el rectángulo que representa el conjunto universal U debe contener 100 objetos. Que x represente a aquellas personas en el conjunto universal que no están ni en el conjunto D ni en K. Esto significa 54 + 6 + 9 + x = 100, o x = 31.
Por lo tanto, hay 31 personas en la encuesta que no han visitado ningún lugar.
Una encuesta a 100 personas conscientes del ejercicio dio como resultado la siguiente información:
- 50 trote, 30 natación y 35 ciclos
- 14 trotar y nadar
- 7 nadar y andar en bicicleta
- 9 trote y ciclo
- 3 personas participan en las tres actividades
- ¿Cuántos trotan pero no nadan ni pedalean?
- ¿Cuántos participan en una sola de las actividades?
- ¿Cuántos no participan en ninguna de estas actividades?
Solución
Que J represente al conjunto de personas que trotan, S el conjunto de personas que nadan y C que pedalean.
Al usar diagramas de Venn, nuestro objetivo final es asignar un número a cada región. Siempre comenzamos asignando primero el número a la región más interna y luego trabajando nuestra salida.
Te mostraremos la solución paso a paso. A medida que practiques resolver tales problemas, encontrarás que con la práctica no necesitarás dibujar múltiples copias del diagrama.
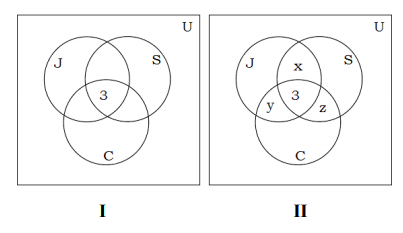
Colocamos un 3 en la región más interna de la figura I porque representa el número de personas que participan en las tres actividades. A continuación utilizamos la figura II para calcular x, y y z.
Ya que 14 personas trotan y nadan, x + 3 = 14, o x = 11.
El hecho de que 9 personas troten y pedaleen da como resultado y + 3 = 9, o y = 6.
Ya que 7 personas nadan y andan en bicicleta, z + 3 = 7, o z = 4.
Esta información se representa en la figura III.
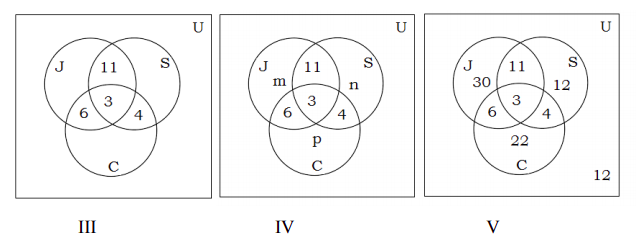
Ahora procedemos a encontrar las incógnitas m, n y p, como se muestra en la figura IV
Desde 50 personas trotan, m + 11 + 6 + 3 = 50, o m = 30.
30 personas nadan, por lo tanto, n + 11 + 4 + 3 = 30, o n = 12.
35 personas ciclo, por lo tanto, p + 6 + 4 + 3 = 35, o p = 22.
Al sumar todas las entradas en los tres conjuntos, obtenemos una suma de 88.
Dado que se encuestaron a 100 personas, el número dentro del conjunto universal pero fuera de los tres conjuntos es de 100 a 88, o 12.
En la figura V, se ordena toda la información, y las preguntas pueden ser respondidas fácilmente.
- El número de personas que trotan pero no nadan ni andan en bicicleta es de 30.
- El número que participan en una sola de estas actividades es de 30 + 12 + 22 = 64.
- El número de personas que no participan en ninguna de estas actividades es de 12.


