1.1.1: Valor posicional y nombres para números enteros
- Page ID
- 111179
- Encuentra el valor posicionar de un dígito en un número entero.
- Escribe un número entero en palabras y en forma estándar.
- Escribe un número entero en forma expandida.
Introducción
Las matemáticas implican resolver problemas que involucran números. Trabajaremos con números enteros, que son cualquiera de los números 0, 1, 2, 3 y así sucesivamente. Primero necesitamos tener un conocimiento profundo del sistema de números que utilizamos. Supongamos que los científicos que preparan un módulo de mando lunar saben que tiene que recorrer 382, 564 kilómetros para llegar a la luna. ¿Qué tan bien les iría si no entendieran este número? ¿Crees que haría más diferencia si el 8 estuviera apagado por 1 o si el 4 fuera por 1?
En esta sección, echarás un vistazo a los dígitos y el valor posicional. También aprenderá a escribir números enteros en palabras, forma estándar y forma expandida en función de los valores posicionales de sus dígitos.
El Sistema Numérico
Un dígito es uno de los símbolos es uno de los símbolos 0, 1, 2, 3, 4, 5, 6, 7, 8 o 9. Todos los números están formados por uno o más dígitos. Los números como 2 tienen un dígito, mientras que los números como el 89 tienen dos dígitos. Para entender lo que realmente significa un número, es necesario entender lo que representan los dígitos en un número dado.
La posición de cada dígito en un número indica su valor, o valor posicional. Podemos usar un gráfico de valor posicional como el siguiente para ver fácilmente el valor posicional de cada dígito. Los valores posicionales para los dígitos en 1, 456 se muestran en este gráfico.
| Trillones | Miles de millones | Millones | Miles | Ones | ||||||||||
| 1 | 4 | 5 | 6 | |||||||||||
| Cientos | Decenas | Ones | Cientos | Decenas | Ones | Cientos | Decenas | Ones | Cientos | Decenas | Ones | Cientos | Decenas | Ones |
En el número 1, 456 el dígito 1 está en el lugar de miles. El dígito 4 está en el lugar de los cientos. El dígito 5 está en el lugar de las decenas, y el dígito 6 está en el lugar de unos.
Como ves arriba, puedes decir el valor de un dígito mirando su posición. Mire el número de dígitos a la derecha del dígito, o escriba su número en un gráfico de valor posicional, con el último dígito en la columna unos. Ambos métodos se muestran en el siguiente ejemplo.
El desarrollo de una ciudad en los últimos veinte años costó $962, 234, 532, 274, 312. ¿Cuál es el valor del dígito 6 en este número?
Solución
| Trillones | Miles de millones | Millones | Miles | Ones | ||||||||||
| 9 | 6 | 2 | 2 | 3 | 4 | 5 | 3 | 2 | 2 | 7 | 4 | 3 | 1 | 2 |
| Cientos | Decenas | Ones | Cientos | Decenas | Ones | Cientos | Decenas | Ones | Cientos | Decenas | Ones | Cientos | Decenas | Ones |
Escriba el número en la tabla de valores posicionados. Lee el valor del 6 del gráfico.
$962, 234, 532, 274, 312
60, 000, 000, 000, 000
Respuesta: El valor del dígito 6 es de 60 billones.
En una galaxia lejana, hay 2, 968, 351, 472 estrellas. ¿Qué representa el dígito 3 en este problema?
- trescientos miles
- tres cientos
- trescientos billones
- trescientos millones
- Contestar
-
- Correcto. El dígito 3 está en el lugar de los cien miles.
- Incorrecto. El dígito 4 está en el lugar de los cientos. La respuesta correcta es de trescientos miles.
- Incorrecto. El número es inferior a un billón, por lo que este dígito no existe aquí. La respuesta correcta es de trescientos miles.
- Incorrecto. El dígito 9 está en el lugar de los cien millones. La respuesta correcta es de trescientos miles.
Periodos y Forma Estándar
La forma estándar de un número se refiere a un tipo de notación en la que los dígitos se separan en grupos de tres por comas. Estos grupos de tres dígitos se conocen como periodos. Por ejemplo, 893, 450, 243 tiene tres periodos con tres dígitos en cada periodo, como se muestra a continuación.
| Trillones | Miles de millones | Millones | Miles | Ones | ||||||||||
| 8 | 9 | 3 | 4 | 5 | 0 | 2 | 4 | 3 | ||||||
| Cientos | Decenas | Ones | Cientos | Decenas | Ones | Cientos | Decenas | Ones | Cientos | Decenas | Ones | Cientos | Decenas | Ones |
Examinemos el número de dígitos y periodos en un número mayor. El número de células del cuerpo en un humano adulto promedio es de aproximadamente cien billones. Este número está escrito como 100, 000, 000, 000, 000. Observe que hay 15 dígitos y 5 periodos. Así es como se vería el número en un gráfico de lugar-valor.
| Trillones | Miles de millones | Millones | Miles | Ones | ||||||||||
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Cientos | Decenas | Ones | Cientos | Decenas | Ones | Cientos | Decenas | Ones | Cientos | Decenas | Ones | Cientos | Decenas | Ones |
Ahora estás familiarizado con los valores posicionales de números mayores, así que examinemos un problema que implica convertir de forma estándar a un nombre de palabra.
Conversión de formularios estándar a nombres de palabras
A menudo usamos nombres de palabras para escribir números. Un nombre de palabra para 42 es “cuarenta y dos”. El número total de semanas en un año, 52, se escribe como “cincuenta y dos”.
Para números enteros con tres dígitos, usa la palabra “cien” para describir cuántos cientos hay en el número. Por ejemplo, para el número de días en un año normal, 365, el dígito 3 está en el lugar de cientos. El nombre de la palabra para el número es “trescientos sesenta y cinco”.
Para números enteros con cuatro dígitos, comience el nombre con el número de miles, seguido del nombre del punto, como en el siguiente ejemplo.
Un hombre debe $2, 562 dólares en un auto. Escribe la palabra nombre para esto.
Solución
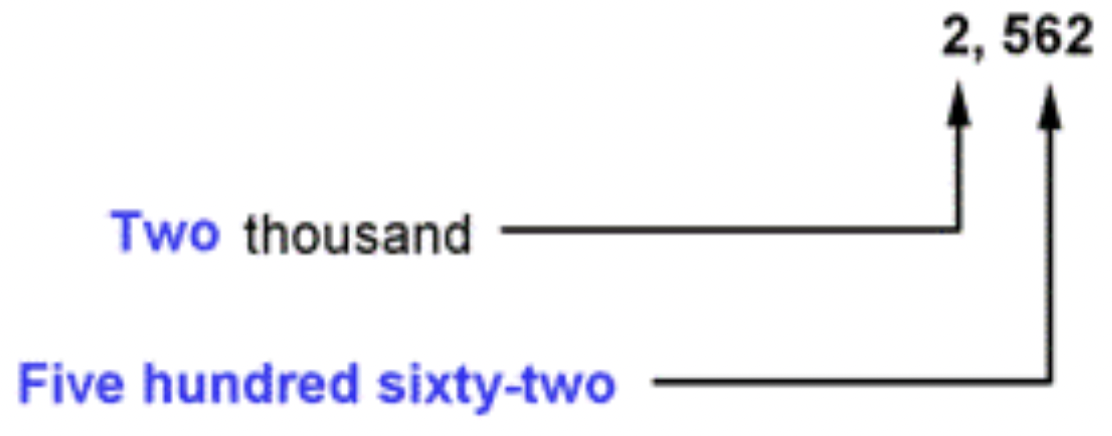
El nombre de la palabra es de dos mil quinientos sesenta y dos.
Para nombres de palabras de números mayores, comienzan por la izquierda con el mayor periodo. Para cada período, escriba el número de uno a tres dígitos en el período y luego el nombre del período. Vea el ejemplo a continuación.
La construcción de un nuevo centro deportivo costó 23, 456, 390 dólares. Escribe el nombre de la palabra para este número.
Solución
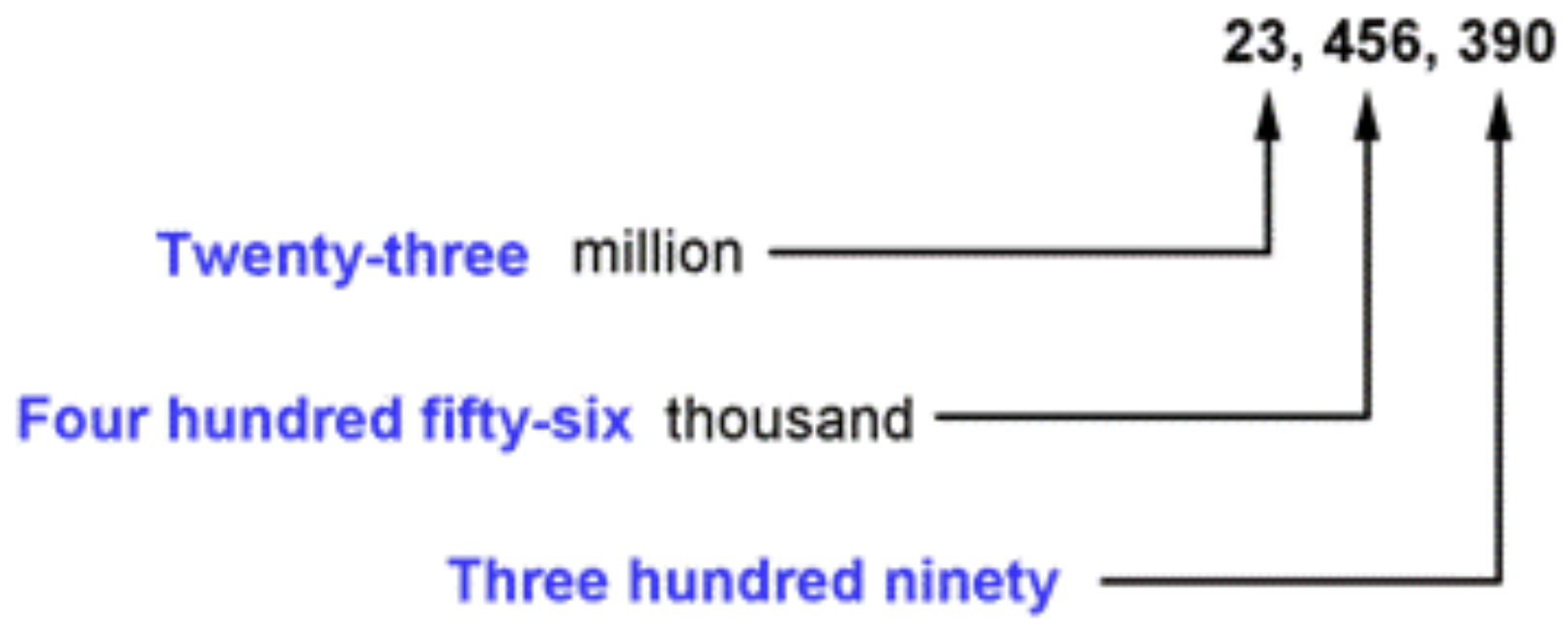
El nombre de la palabra es veintitrés millones, cuatrocientos cincuenta y seis mil trescientos noventa.
Conversión de nombres de palabras a forma estándar
Al convertir nombres de palabras a forma estándar, la palabra “mil” te dice en qué período se encuentran los dígitos. Vea el ejemplo a continuación.
Cuarenta y siete mil quinientos ochenta y seis arándanos se producen en una finca en el transcurso de tres años. Escribe este número en forma estándar.
Solución
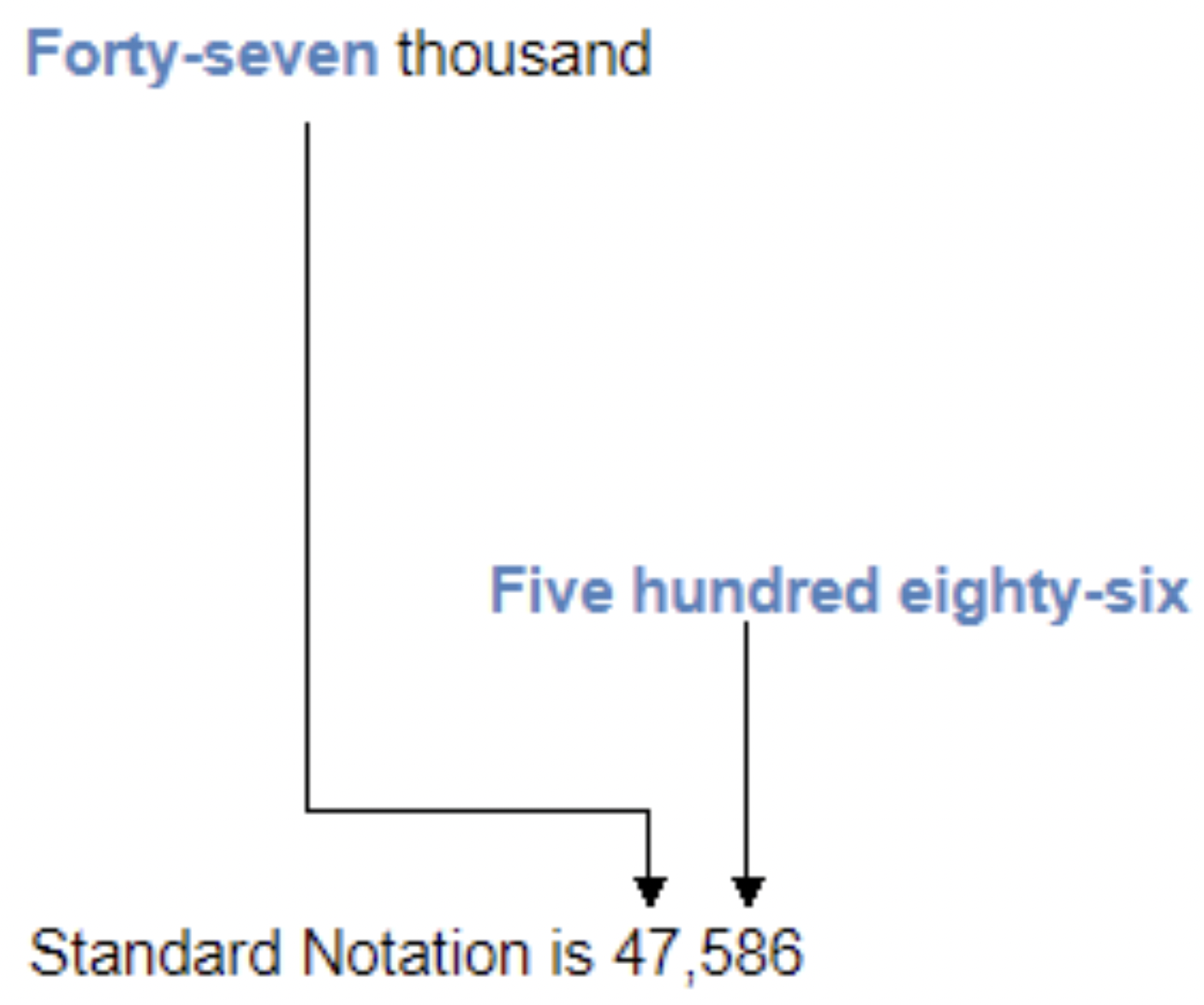
El número en forma estándar es 47, 586.
A continuación se muestra un ejemplo con un número que contiene más dígitos. Las palabras “millón” y “mil” te indican en qué periodos se encuentran los dígitos. Los periodos están separados por comas.
Hay trescientos ocho millones, seiscientos treinta y dos mil novecientos setenta y ocho bacterias en una muestra de suelo. Escribe este número en forma estándar.
Solución
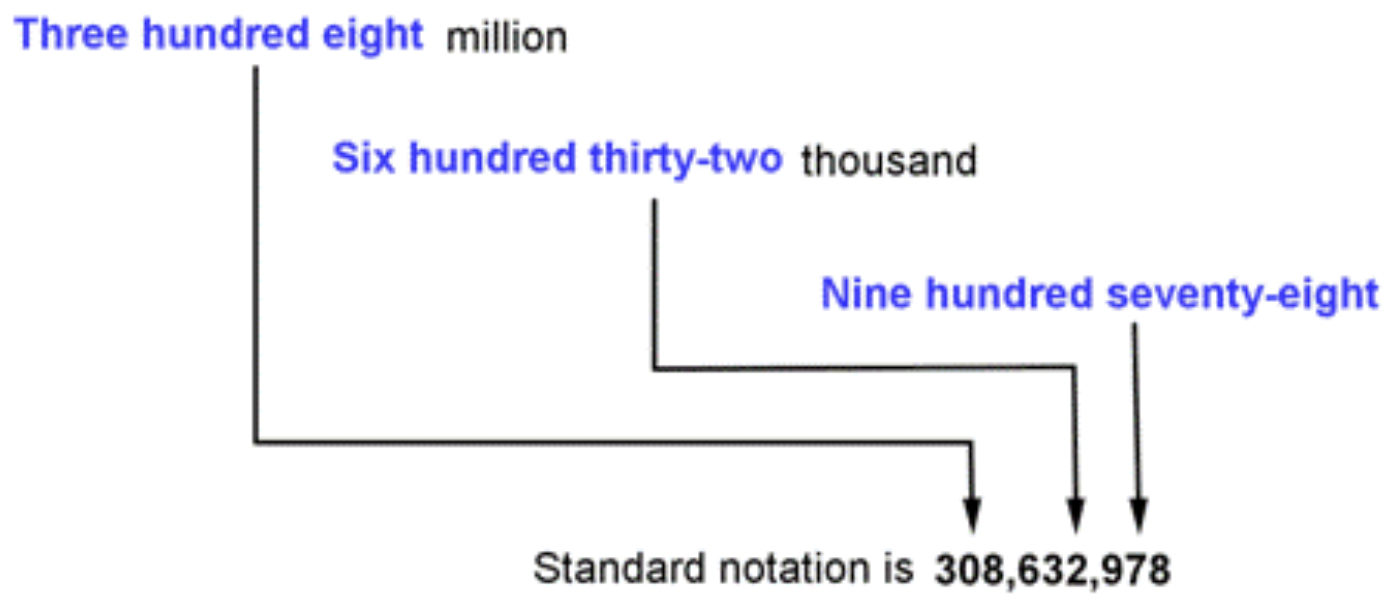
El número en forma estándar es 308, 632, 978
Algunos números en forma de palabras pueden no mencionar un período específico. Por ejemplo, tres millones, ciento doce escritos en forma estándar es 3, 000, 112. Debido a que no se menciona el periodo de miles, escribirías tres ceros en el periodo de miles. Puedes usar un gráfico de valor posicional para que sea más fácil ver los valores de los dígitos. Vea el ejemplo a continuación.
Una empresa tenía construido un nuevo edificio de oficinas. El costo final fue de setenta y cuatro millones, trescientos sesenta y dos dólares. Escribe este número en forma estándar.
Solución
| Trillones | Miles de millones | Millones | Miles | Ones | ||||||||||
| 7 | 4 | 0 | 0 | 0 | 3 | 6 | 2 | |||||||
| Cientos | Decenas | Ones | Cientos | Decenas | Ones | Cientos | Decenas | Ones | Cientos | Decenas | Ones | Cientos | Decenas | Ones |
Al colocar este número en un gráfico de valor posicional, se muestra que el periodo de miles es cero.
Recuerda separar cada periodo con una coma.
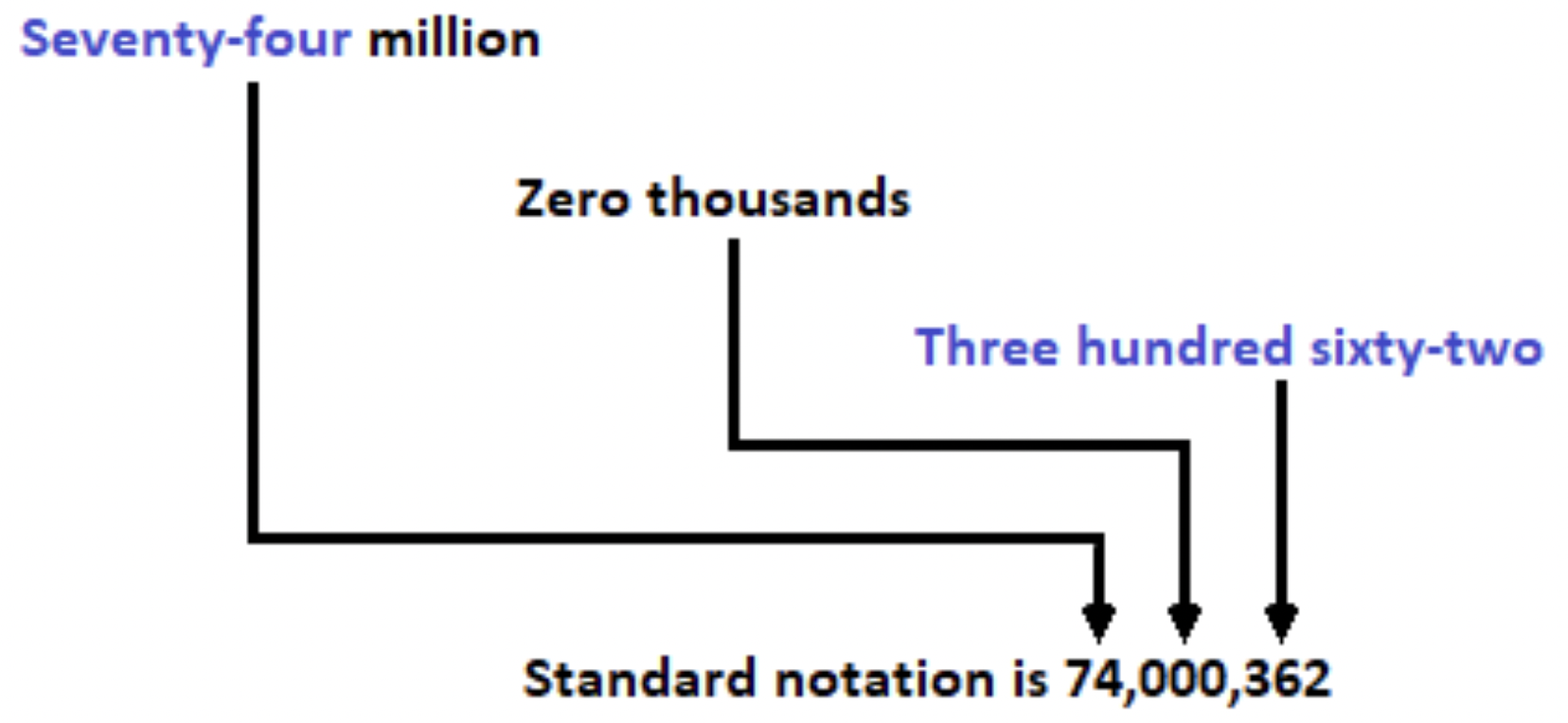
El número escrito en forma estándar es de 74, 000, 362 dólares.
Escribir números en forma expandida
A veces es útil escribir números en forma expandida. En forma expandida, el número se escribe como una suma del valor de cada dígito.
Durante la semana, Mike conduce un total de 264 millas. Escribe 264 en forma expandida.
Solución
Primero, identificar el valor de cada dígito.
| En forma numérica: | |
| El 2 en 264 | 200 |
| El 6 en 264 | 60 |
| El 4 en 264 | 4 |
| En forma de palabras: | |
| El 2 en 264 | 2 cientos |
| El 6 en 264 | 6 decenas |
| El 4 en 264 | 4 unos |
| Después, escribe los números como una suma. |
264 escrito en forma expandida es
200 + 60 + 4 o
2 cientos + 6 decenas + 4 o
\(\ (2 \cdot 100)+(6 \cdot 10)+(4 \cdot 1)\)
También puedes usar una tabla de valor posicional para ayudar a escribir un número en forma expandida. Supongamos que el número de autos y camionetas pick-up en Estados Unidos en este mismo momento es de 251,834,697. Coloca este número en un gráfico de valores posicionados.
| Trillones | Miles de millones | Millones | Miles | Ones | ||||||||||
| 2 | 5 | 1 | 8 | 3 | 4 | 6 | 9 | 7 | ||||||
| Cientos | Decenas | Ones | Cientos | Decenas | Ones | Cientos | Decenas | Ones | Cientos | Decenas | Ones | Cientos | Decenas | Ones |
| 2 mil millones | 200,000,000 |
| +5 diez millones | +50,000,000 |
| +1 millón | +1,000,000 |
| +8 cientos miles | +800,000 |
| +3 diez miles | +30,000 |
| +4 miles | +4,000 |
| +6 cientos | +600 |
| +9 decenas | +90 |
| +7 unos | +7 |
Resumen
Los números enteros que son mayores a 9 constan de múltiples dígitos. Cada dígito en un número dado tiene un valor positorio. Para comprender mejor el valor posicional, los números se pueden poner en un gráfico de valor posicional para que se pueda identificar el valor de cada dígito. Los números con más de tres dígitos se pueden separar en grupos de tres dígitos, conocidos como periodos. Cualquier número entero se puede expresar en forma estándar, forma expandida o como un nombre de palabra.


