1.1.2: Redondeo de números enteros

Última actualización
Guardar como PDF

Page ID: 111185

The NROC Project

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

Aprende las reglas para redondear.
Redondea números enteros a valores posicionar específicos, incluyendo decenas, cientos y miles.

Introducción

En algunas situaciones, no necesitas una respuesta exacta. En estos casos, es posible redondear el número a un valor posicionar específico. Por ejemplo, si viajó 973 millas, es posible que desee redondear la distancia a 1,000 millas, lo que es más fácil de pensar. El redondeo también es útil para ver si un cálculo es razonable.

Redondeo de números enteros

Estas son las reglas para redondear números enteros:

Primero, identifique el dígito con el valor posicionar al que esté redondeando. Podrías rodear o resaltar el dígito para que puedas enfocarte mejor en él.

Después, determina los posibles números que obtendrías redondeando. Estos posibles números están cerca del número al que estás redondeando, pero tienen ceros en los dígitos a la derecha.

Si estás redondeando 186 al diez más cercano, entonces 180 y 190 son los dos números posibles a redondear, ya que 186 está entre 180 y 190. Pero, ¿cómo sabes si redondear a 180 y 190?

Por lo general, redondea un número al número más cercano al número original.

Cuando un número está a medio camino entre los dos números posibles, redondea al número mayor.

Dado que 186 está entre 180 y 190, y 186 está más cerca de 190, redondea hasta 190.

Puedes usar una línea numérica para ayudarte a redondear números.

Ejemplo

Se deja caer una cámara de un bote y se hunde hasta el fondo de un estanque que tiene 37 pies de profundidad. Vuelta 37 a la diez más cercana.

Solución

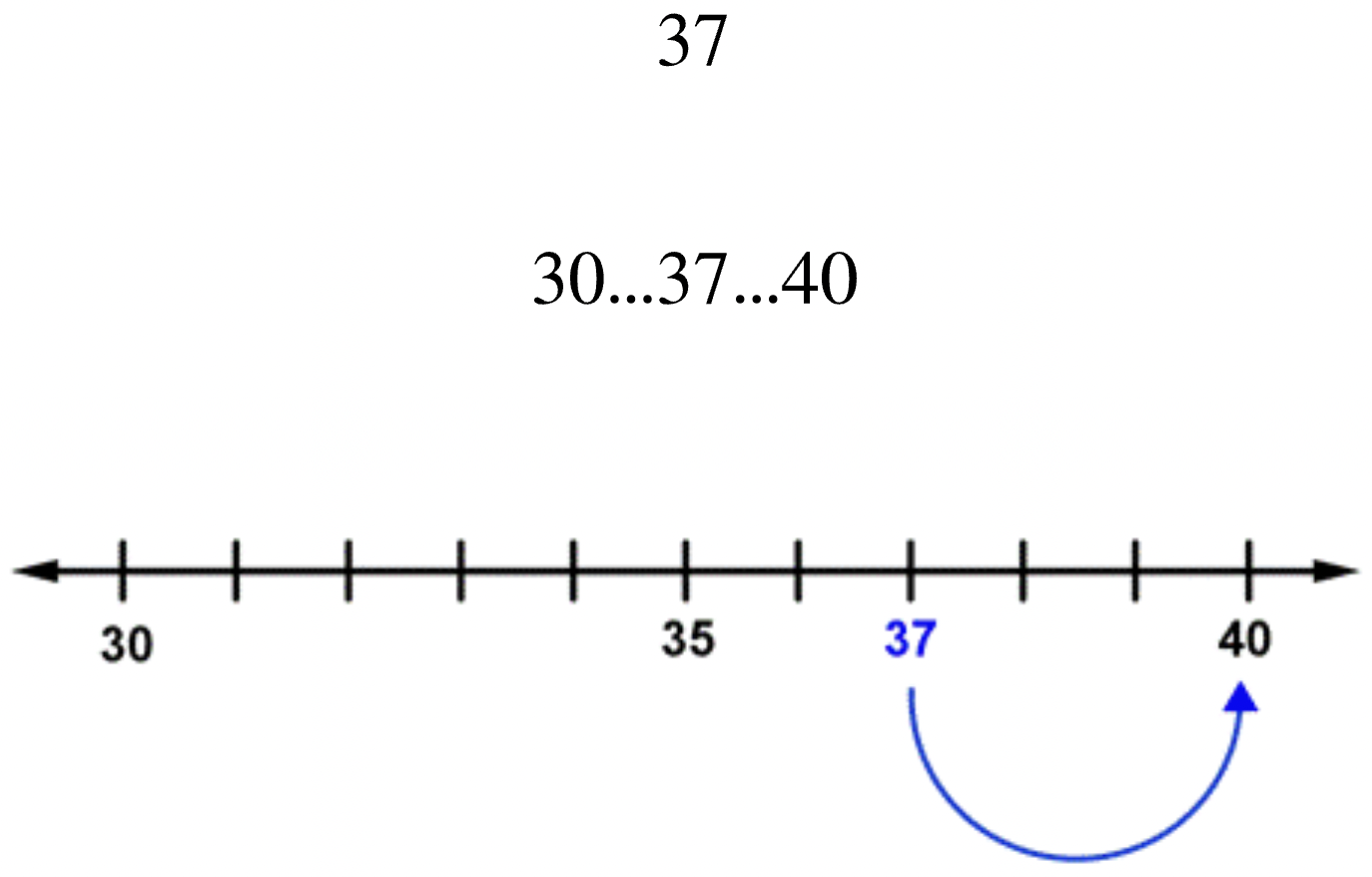
$Screen Shot 2021-04-06 a las 12.16.13 PM.png$

El dígito al que estás redondeando es el dígito de las decenas, 3.

37 es entre 30 y 40.

37 está a solo 3 de 40, pero es 7 de 30. Entonces, 37 está más cerca de 40.

Al diez más cercano, 37 rondas a 40.

Ejemplo

Vuelta 33 a la diez más cercana.

Solución

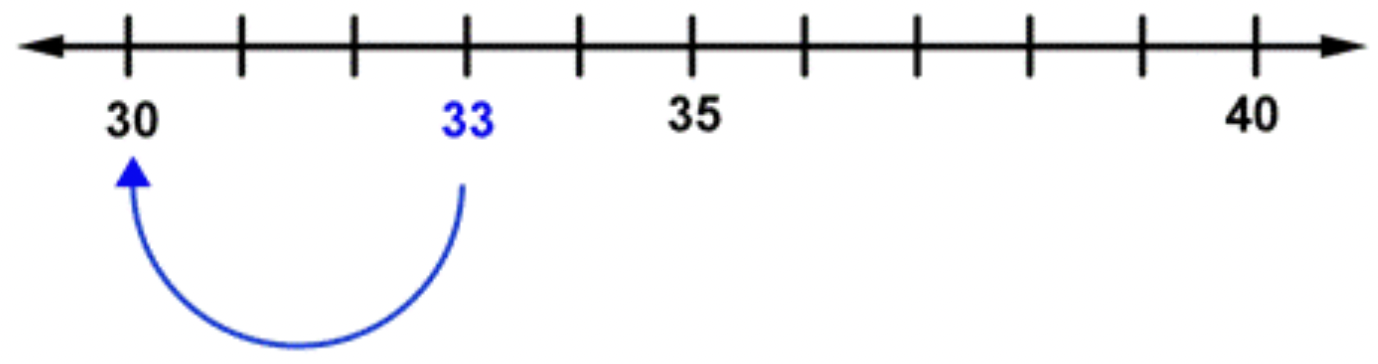
$Screen Shot 2021-04-06 at 12.22.04 PM.png$

33 rondas a 30 porque 33 está más cerca de 30.

Al diez más cercano, 33 rondas a 30.

Puedes determinar dónde redondear sin usar una línea numérica mirando el dígito a la derecha del que estás redondeando. Si ese dígito es menor que 5, redondea hacia abajo. Si es 5 o más, redondea hacia arriba. En el ejemplo anterior, se puede ver sin una línea numérica que 33 se redondea a 30 porque el dígito unos, 3, es menor que 5.

Ejemplo

Vuelta 77 a la diez más cercana.

Solución

77 redondea a 80 porque el dígito unos, 7, es 5 o mayor.

77 redondeado al diez más cercano es 80.

Ejemplo

Hay 576 jaleas en un frasco. Redondea este número al diez más cercano.

Solución

576 redondea a 580 porque el dígito unos, 6, es 5 o mayor.

576 redondeado al diez más cercano es 580.

En los ejemplos anteriores, redondeaste al lugar de las decenas. Los números redondeados tuvieron un 0 en el lugar de unos. Si redondea al cien más cercano, el número redondeado tendrá ceros en los lugares de decenas y unos. El número redondeado se asemejará a 100, 500 o 1, 200.

Ejemplo

Un corredor corrió 1,539 metros, pero describe la distancia que corrió con un número redondeado. Redondea 1,539 al cien más cercano.

Solución

1,539 redondea a 1,500 porque el siguiente dígito es menor que 5.

1,539 redondeado al cien más cercano es de 1,500.

Si redondea al mil más cercano, el número redondeado tendrá ceros en los lugares de cientos, decenas y unos. El número redondeado se asemejará a 1,000, 2,000 o 14,000.

Ejemplo

La altitud de un avión aumentó 2,721 pies. Redondear este número al mil más cercano.

Solución

2,721 redondea a 3,000 porque el siguiente dígito, 7, es 5 o mayor.

2 mil 721 redondeados al mil más cercano es de 3 mil.

Ahora que ya sabes redondear a los diez, cien y mil más cercanos, intenta redondear a los diez mil más cercanos.

Ejemplo

Vuelta 326,749 a los diez mil más cercanos.

Solución

326,749 redondea a 330,000 porque el siguiente dígito, 6, es 5 o mayor.

326,749 redondeado a los diez mil más cercanos es de 330.000.

Ejercicio

Un número récord de 23,386 personas votaron en una elección de ciudad. Redondea este número al cien más cercano.

23,300
23,400
23,000
23,390

Contestar

Incorrecto. Los dos números posibles son 23,300 y 23,400, pero 23,386 está más cerca de 23,400. El dígito de las decenas, 8, es 5 o mayor, por lo que debes redondear hacia arriba. La respuesta correcta es 23,400.
Correcto. Los dos números posibles son 23,300 y 23,400, y 23,386 está más cerca de 23,400. El dígito de las decenas, 8, es 5 o mayor, por lo que debes redondear hacia arriba.
Incorrecto. Este número se redondea al mil más cercano, no al cien más cercano. La respuesta correcta es 23,400.
Incorrecto. Este número se redondea al diez más cercano, no al cien más cercano. La respuesta correcta es 23,400.

Resumen

En situaciones en las que no necesitas una respuesta exacta, puedes redondear números. Cuando redondea números, siempre está redondeando a un valor posicionar determinado, como el mil más cercano o el diez más cercano. El redondear hacia arriba o hacia abajo generalmente depende de qué número es el más cercano a su número original. Cuando un número está a medio camino entre los dos números posibles, redondee al número mayor.