1.3.1: Multiplicar números enteros y aplicaciones
( \newcommand{\kernel}{\mathrm{null}\,}\)
- Usa tres formas diferentes de representar la multiplicación.
- Multiplicar números enteros.
- Multiplica números enteros por una potencia de 10.
- Use redondeo para estimar productos.
- Encuentra el área de un rectángulo.
- Resolver problemas de aplicación usando multiplicación.
Introducción
En lugar de agregar el mismo número una y otra vez, una manera más fácil de llegar a una respuesta es usar la multiplicación. Supongamos que quiere encontrar el valor en centavos de 9 nickels. Puedes usar la adición para resolverlo. Dado que un níquel vale 5 centavos, o 5 centavos, puedes encontrar el valor de 9 nickels sumando 5+5+5+5+5+5+5+5+5. Esta adición repetida muestra que 9 nickels tienen un valor de 45 centavos.
Toda esta adición puede llegar a ser muy agotadora. Entonces, la operación matemática llamada multiplicación puede ayudar a realizar la adición repetida de números enteros mucho más rápidamente. Para encontrar el valor de estas monedas de cinco centavos, podrías escribir una ecuación de multiplicación: 5⋅9=45.
5⋅9=45se lee “5 veces 9 es igual a 45" o “5 multiplicado por 9 es igual a 45”. A los números que se están multiplicando se les llama factores. Los factores en este ejemplo son 5 y 9. El resultado de la multiplicación (o la respuesta) se llama el producto. El producto para 5⋅9 es 45.
Además de mostrar la multiplicación como 5⋅9=45, se puede mostrar la multiplicación usando el signo x, 5×9=45, y también con paréntesis, (5) (9) = 45 o 5 (9) =45.
Tres formas de escribir multiplicación
Usando un signo de multiplicación o tiempos: 2×3=6
Usando un punto: 2⋅3=6 (este punto NO es un punto decimal)
Usando paréntesis: (2) (3) =6 o 2 (3) =6
Cuando estás agregando el mismo número una y otra vez, puedes usar la multiplicación. Toma el número que estás agregando y lo reescribes como problema de multiplicación, multiplicándolo por el número de veces que lo estás agregando. Por ejemplo, si estuvieras sirviendo 2 galletas cada una a 13 niños, podrías agregar 2 trece veces o podrías usar la multiplicación para encontrar la respuesta.
2+2+2+2+2+2+2+2+2+2+2+2+2=2⋅13=26
También podrías escribir esto usando paréntesis: 2(13)=26
¿Qué es la multiplicación?
Para entender qué es la multiplicación, considera tres formas diferentes de pensar sobre la multiplicación de números enteros.
Enfoque 1: Establecer modelo
La multiplicación es una forma de escribir la adición repetida. Cuando lees el problema 3⋅5 podrías pensar en esto como 3 grupos de 5 cosas: 3 platos con 5 galletas en cada plato; 3 canastas, cada una con 5 naranjas en él; o 3 pilas con 5 monedas en cada pila. Podríamos mostrar esto como una imagen:
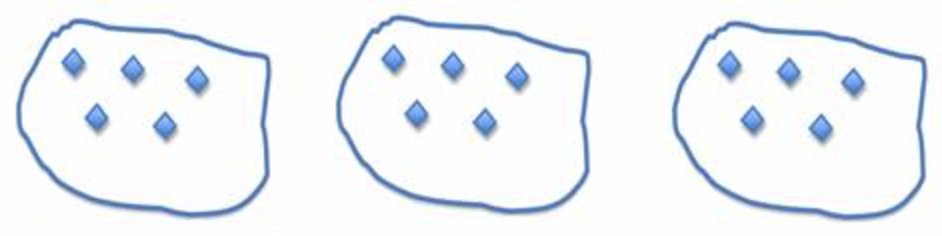
3⋅5=3grupos de 5=15
Enfoque 2: Modelo de línea numérica
La multiplicación también se puede mostrar en una recta numérica. El problema, 3⋅5 se modela en la línea numérica de abajo. Se puede ver que las flechas cubren una distancia de 5 unidades a la vez. Después de 3 “saltos” en la recta numérica, la flecha termina en 15.
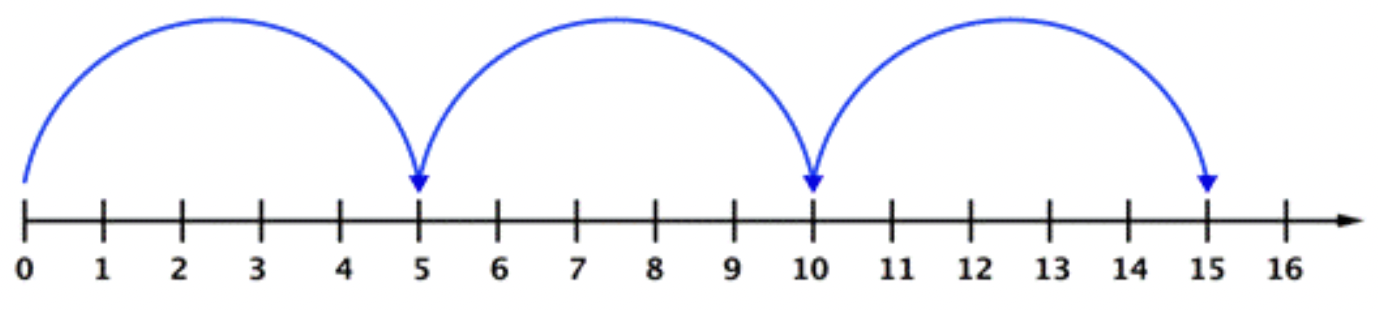
Enfoque 3: Modelo de área
Otra forma de pensar sobre la multiplicación es pensar en una matriz o modelo de área para representar la multiplicación. Se podría pensar en 3 filas de 5 cosas. 3⋅5 Esto podría ser una caja de chocolates que tiene 3 filas de 5 chocolates, o una sala de reuniones que se configura con 3 filas de 5 sillas. Las imágenes a continuación muestran dos arreglos rectangulares de 3⋅5.
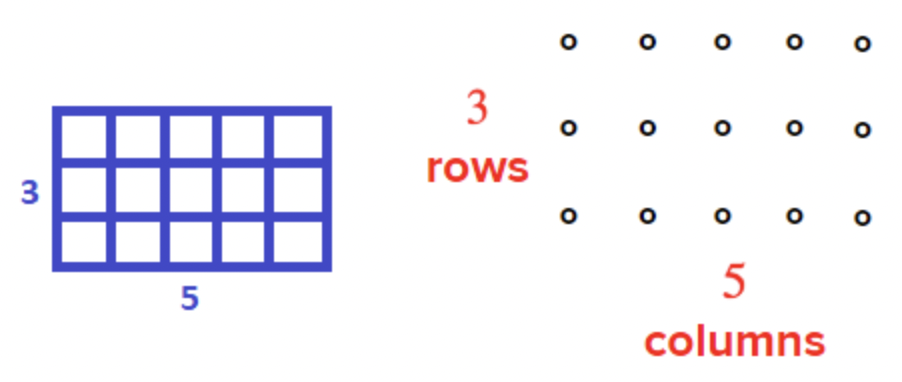
¿Ves como ambas imágenes representan el producto 15? La imagen de la izquierda muestra un área de 3 por 5. Si cuentas los cuadrados pequeños que conforman el rectángulo, suman 15. De igual manera, en la imagen de la derecha, se ve que 3 filas de 5 círculos es igual a 15 círculos.
¿De qué es el producto 4⋅6? Utilice el modelo de conjunto, el modelo de línea numérica y el modelo de área para representar el problema de multiplicación.
Solución
Modelo de conjunto:
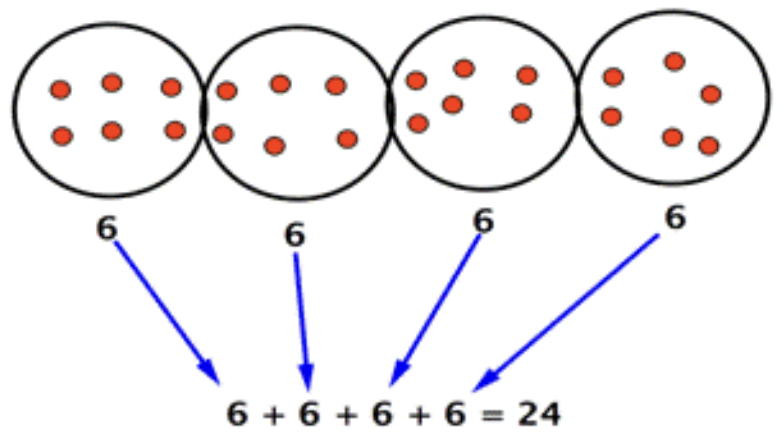
Modelo de línea numérica:
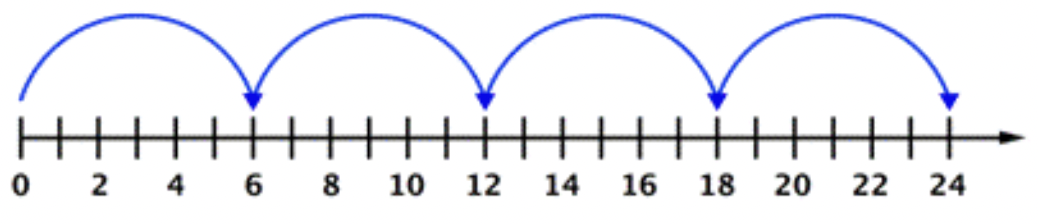
Modelo de área:
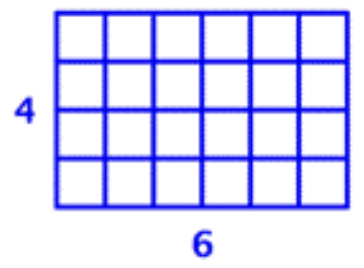
4⋅6=24
Si cambias el orden en el que multiplicas dos números, el producto no cambiará. Esto es cierto para dos números cualesquiera que multipliques. Piense en el problema que se muestra arriba.
Podrías hacer 6 saltos de 4 o 4 saltos de 6 en la línea numérica y terminar en 24.
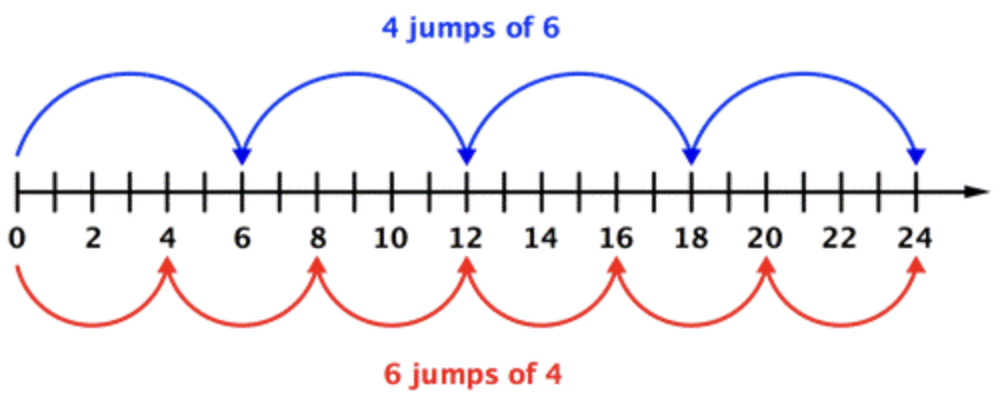
O bien, podrías hacer 6 filas de 4 o 4 filas de 6 y aún así tener 24 cuadrados.
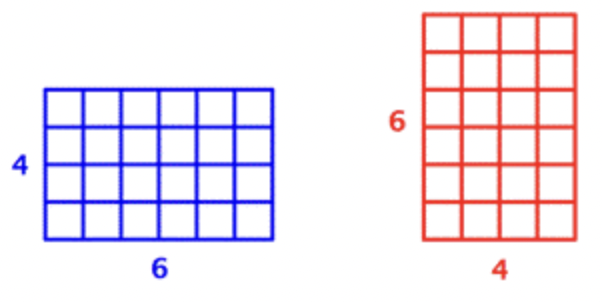
6⋅4=24y 4⋅6=24.
Tanisha modeló 5⋅8 usando los siguientes modelos. ¿Qué modelos son representaciones precisas de la multiplicación de estos dos factores?
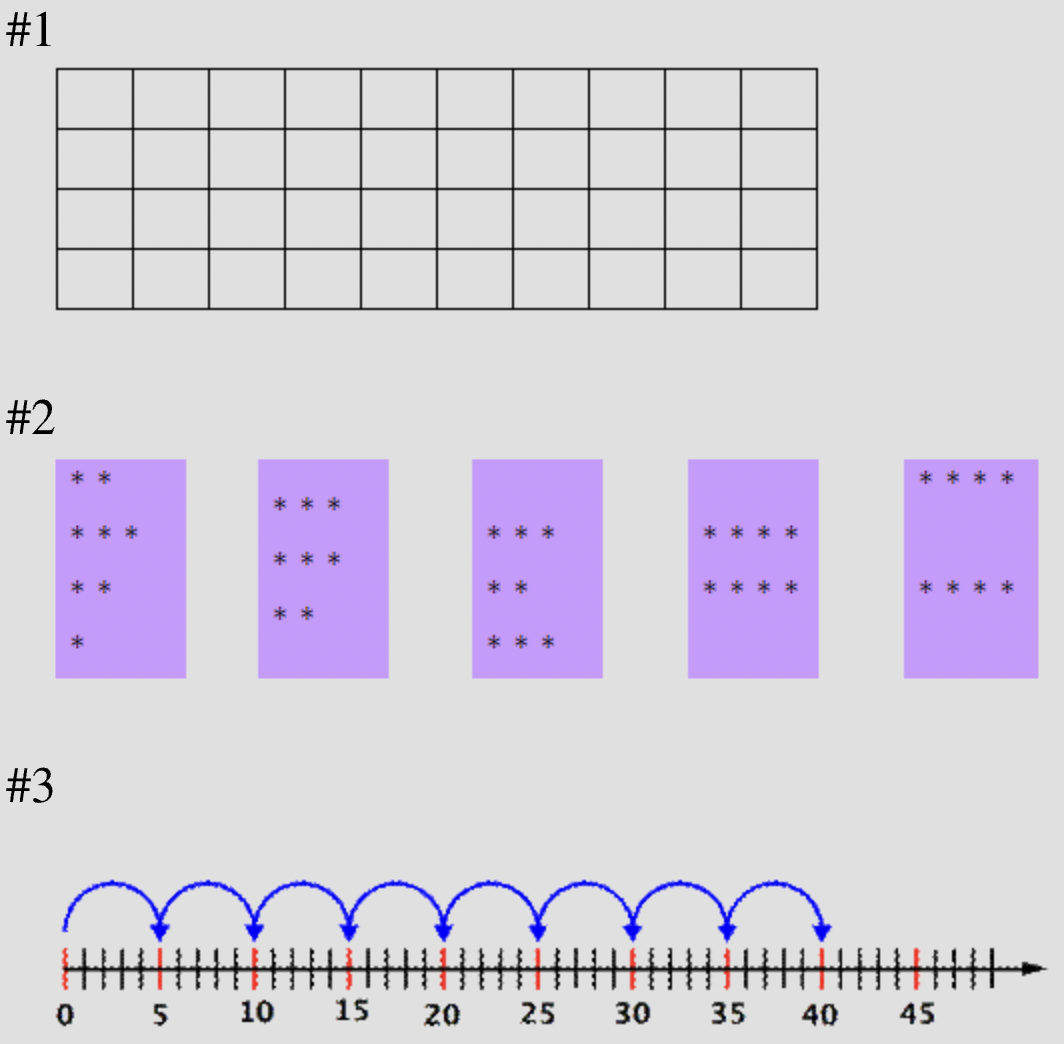
- Los tres modelos representan con precisión 5⋅8.
- Solo los modelos #1 y #3 representan con precisión 5⋅8.
- Solo los modelos #2 y #3 representan con precisión 5⋅8.
- Ninguno de los modelos representa con precisión 5⋅8.
- Contestar
-
- Los tres modelos representan con precisión 5⋅8. Incorrecto. Si bien el primer modelo tiene el mismo producto, modela los factores 4⋅10. La respuesta correcta es Solo los modelos #2 y #3 representan con precisión 5⋅8.
- Solo los modelos #1 y #3 representan con precisión 5⋅8. Incorrecto. Modelo #1 modelos 4⋅10, no 5⋅8. La respuesta correcta es Solo los modelos #2 y #3 representan con precisión 5⋅8.
- Solo los modelos #2 y #3 representan con precisión 5⋅8. Correcto. El modelo #2 muestra 5 grupos de 8, lo que equivale a 40. El modelo #3 muestra saltar contando 8 veces por 5 para llegar a 40.
- Ninguno de los modelos representa con precisión 5⋅8. Incorrecto. Los modelos #2 y #3 representan la multiplicación 5⋅8. La respuesta correcta es Solo los modelos #2 y #3 representan con precisión 5⋅8.
Multiplicar números mayores
Volvamos a la pregunta planteada en la apertura de este tema de estudio. ¿Cómo se puede usar la multiplicación para calcular el costo total de 6 gorras de béisbol que cuestan 14 dólares cada una? (No tiene que pagar impuesto sobre las ventas). Se puede calcular el costo multiplicando 14⋅6.
Una forma de hacer este cálculo es descomponer 14 en partes y multiplicar cada parte por 6.
\ (\\ begin {alineado}
14 &=10+4\ quad\ text {Así,}\\
14\ cdot 6 &=10\ cdot 6+4\ cdot 6\\
&=60+24\
&=84
\ end {alineado}\)
Puede recordar la multiplicación calculada como 14⋅6:
\ (\\ begin {array} {r}
2\\
14\
\ veces\ quad 6\\
\ hline 84
\ end {array}\)
En esta notación, algunos de los pasos están escritos con notación especial. El producto de 6 y 4 (24) se escribe poniendo el 4 en el lugar unos y escribiendo un 2 arriba del 1. Este 2 en realidad representa 20. Entonces, 6 se multiplica por 1. En realidad estamos multiplicando 6 por 1 diez y sumando 20 para conseguir el 80 en 84.
A continuación se muestra un ejemplo de multiplicar dos números de dos dígitos. Al realizar esta multiplicación, cada parte de cada número se multiplica por el otro número. Se proporciona la notación numérica y una descripción adjunta.
47⋅52
Solución
| \ (\\ begin {array} {r} 47\\ \ times\ quad 52\\ \ hline \ end {array}\) |
Apila los números con los valores de posición alineados. |
| \ (\\ begin {array} {r} \ color {azul} 1\\\\ 4\ color {rojo} 7\\ \ veces\ quad 5\ color {rojo} 2\\ \ hline\ color {azul} 4 \ end {array}\) |
Multiplicar los unos. 2×7=14unos. Escribe 4 en el lugar de unos y reagrupa 10 en el lugar de las decenas. |
| \ (\\ begin {array} {r} \ color {rojo} 1\\\\ {\ color {rojo} 4} 7\\ \ veces\ quad 5\ color {rojo} 2\\ \ hline {\ color {azul} 9} 4 \ end {array}\) |
Multiplica 2 unos por 4 decenas, y agrega los reagrupados 1 diez. 2 unos por 4 decenas + 1 diez = 9 decenas |
| \ (\\ begin {array} {r} \ color {azul} 3\\\\\\ 4\ color {rojo} 7\\ \ veces\ quad {\ color {rojo} 5} 2\\ \ hline 94\\ \ color {azul} 50 \ end {array}\) |
Multiplicar las decenas. 5×7=35decenas. Escribe 5 decenas en el lugar de las decenas y reagrupa. |
| \ (\\ begin {array} {r} \ color {azul} 3\\\\\\\ {\ color {rojo} 4} 7\\ \ veces {\ color {rojo} 5} 2\\ \ hline 94\\ {\ color {azul} 23} 50 \ end {array}\) |
Multiplicar: 5 decenas por 4 decenas = 20 cientos. Agregar el 3 reagrupado, que es de 3 cien. |
| \ (\\ begin {array} {r} 3\\\\\\\\ {\ color {rojo} 4} 7 \\\ veces\ quad {\ color {rojo} 5} 2 \\\ hline\ color {azul} 1\ color {rojo} 94 \\ color {rojo} 2350\ \ hline\ color {azul} 2,444 \ end {array}\) |
Sumar las dos líneas. 94+2,350 |
47⋅52=2,444
Observe que está multiplicando cada una de las partes de cada número por las partes del otro número. Lo estás haciendo de manera sistemática, de unos lugares a decenas de lugares. También estás usando la notación para hacer un seguimiento de lo que has reagrupado. Estos se muestran con números elevados.
Para mantener tus columnas rectas y tu trabajo organizado, considera usar papel de rejilla o papel rayado girado hacia los lados para que las líneas formen columnas. Aquí hay un ejemplo de un problema escrito en papel de rejilla:
\ (\\ begin {array} {|l|l|l|l|}
\ hline & & & 2 & 3\\ hline &
\ mathrm {x} & 1 & 2\\ hline & &\
color {azul} 4 &\ color {azul} 6\\ hline+ &\ color {azul} 2 &
\ color {azul} 3 &\ color {azul} 0\\ hline+ &\ color {azul} 0\ hline+ &
\ color {azul} línea y amp;\ color {rojo} 2 &\ color {rojo} 7 &\ color {rojo} 6\\
\ hline
\ end {array}\)
Cuando esté multiplicando números enteros, asegúrese de alinear los dígitos por sus valores posicionados. En el ejemplo anterior, los dígitos en el lugar de unos están alineados: el 2 en 12 está directamente por debajo del 3 en 23.
Multiplicar números enteros por 10
Cuando multiplicas números por 10 o potencias de 10 (100; 1,000; 10,000; 100,000), descubrirás algunos patrones interesantes. Estos patrones ocurren porque nuestro sistema de números se basa en diez: diez unos equivalen a diez; diez decenas equivalen a cien; diez cientos equivalen a mil. Aprender sobre estos patrones puede ayudarle a calcular fácil y rápidamente.
Considera el ejemplo de 25⋅100. Primero, usemos el método del algoritmo estándar para multiplicar estos números.
25⋅100
Solución
\ (\\ begin {array} {r}
100\
\\ times\ quad 25\
\ hline 500\\
2000\
\ hline 2,500
\ end {array}\)
25⋅100=2,500
Usando el algoritmo estándar, calculamos 25⋅100=2,500.
Mira la tabla a continuación para encontrar un patrón en los factores y productos. Vea cómo el número de ceros en la potencia de 10 (10,100, 1,000, etc.) se relaciona con el número de ceros en el producto.
| Factores | Producto |
| 5⋅10 | = 50 |
| 5⋅100 | = 500 |
| 5⋅1,000 | = 5,000 |
| 5⋅10,000 | = 50.000 |
Se puede ver que el número de ceros en el producto coincide con el número de ceros en la potencia de 10 (10,100,1,000, etc.). ¿Será esto siempre cierto o es cierto sólo en ciertas situaciones? Mira dos patrones más:
| Factores | Producto |
| 10⋅10 | = 100 |
| 10⋅100 | = 1,000 |
| 10⋅1,000 | = 10,000 |
| 10⋅10,000 | = 100,000 |
| Factores | Producto |
| 120⋅10 | = 1.200 |
| 120⋅100 | = 12.000 |
| 120⋅1,000 | = 120,000 |
| 120⋅10,000 | = 1,200,000 |
Observe que en estos dos últimos ejemplos, ambos factores tenían ceros en ellos. El número de ceros en el producto es igual a la suma del número de ceros al final de cada uno de los factores.
El siguiente ejemplo ilustra cómo multiplicar 140⋅3000.
140⋅3000
Solución
| \ (\\ begin {array} {r} \ color {azul} 1\\\\ 14\ \\ veces\ quad 3\ \ hline\ color {azul} 42 \ end {array}\) |
Identificar las partes distintas de cero de los factores y multiplicar estas partes. Multiplica 3 unos por 4 unos. 4⋅3=12. |
| 420,000 |
Contar el número de ceros en cada factor. 140 tiene un cero; 3,000 tiene tres ceros. 1+3=4 Escribe otros 4 ceros después del 42. |
140⋅3000=420,000
Cuando multiplicas un número entero por 10 o una potencia de 10, primero multiplica las partes distintas de cero de los números. Luego incluya el número de ceros al final del producto igual al número total de ceros al final de los factores.
13⋅100=1,300
180⋅2,000=360,000
Un huerto de manzanas vendía 100 bolsas de manzanas. Si hay 30 manzanas en cada bolsa, ¿cuántas manzanas vendió el huerto?
- 130
- 300
- 30,000
- 3,000
- Contestar
-
- Incorrecto. Es necesario multiplicar 100 y 30, no sumar. La respuesta correcta es de 3,000.
- Incorrecto. 30⋅100=3,000. No se incluyó el número correcto de ceros. La respuesta correcta es de 3,000.
- Incorrecto. 30⋅100=3,000. Incluyeron demasiados ceros. La respuesta correcta es de 3,000.
- Correcto. 30⋅100=3,000.3⋅1=3y sumar tres ceros ya que hay uno cero en 30 y hay dos ceros en 100.
Uso del redondeo para estimar productos
A veces no necesitas un producto exacto porque una estimación es suficiente. Si estás de compras, pararte a hacer un cálculo con lápiz y papel, o incluso con una calculadora, es inconveniente. Por lo general, los compradores redondearán los números para que estén seguros de que tienen suficiente dinero para sus compras.
Estimar productos también es útil para verificar una respuesta a un problema de multiplicación. Si tu cálculo real es bastante diferente de tu estimación, es muy probable que hayas cometido un error de valor posicional y/o reagrupamiento.
Para estimar un producto, a menudo redondea primero los números. Cuando redondeas números, siempre estás redondeando a un valor posicional particular, como el mil más cercano o el diez más cercano. Si estás redondeando un número al diez más cercano, lo redondeas al diez que está más cerca del número original. Un ejemplo de ello es redondear 317 al diez más cercano. En este caso, rondas 317 a 320. Si el número está a medio camino entre (315), generalmente redondea hasta 320.
Los factores de redondeo pueden facilitar la multiplicación en tu cabeza. Consideremos el problema de la multiplicación 145⋅29. Para estimar este producto por redondeo, puedes redondear al diez más cercano.
Utilice redondeo para estimar el producto de 145⋅29.
Solución
| 150⋅30 | Redondear los números al diez más cercano. |
| 15⋅3=45 | Multiplique los números distintos de cero. |
| 4,500 | Contar los ceros en los factores e incluir tantos ceros después de los 45. |
La estimación de 145⋅29 is 4,500.
Puedes usar una calculadora para ver si tu estimación parece razonable. O puedes usar estimación para asegurarte de que la respuesta que obtuviste en una calculadora sea razonable. (¿Alguna vez has introducido los números equivocados?)
|
Entradas clave: 145 x 29 = Resultado: 4,205 El producto exacto y la estimación están lo suficientemente cerca como para darle confianza en sus cálculos. |
Una fábrica produce 58 paquetes de galletas en una hora. Hay 32 galletas en cada paquete. ¿Cuál es la mejor estimación del número de galletas que produce la fábrica en una hora?
- 1,800
- 1,500
- 18,000
- 180
- Contestar
-
- Correcto. Multiplicar 60⋅30 daría una buena estimación. 60⋅30=1,800.
- Incorrecto. 50⋅30=1,500, pero 58 rondas a 60, no 50.La respuesta correcta es 1,800.
- Incorrecto. 60⋅30=1,800. La respuesta correcta es 1,800.
- Incorrecto. 60⋅30=1,800. La respuesta correcta es 1,800.
Encontrar el área de un rectángulo
La fórmula para el área de un rectángulo utiliza la multiplicación: length ⋅ width = area . Aplicando lo que sabes de multiplicación, puedes encontrar el área de cualquier rectángulo si conoces sus dimensiones (largo y ancho). Considera el rectángulo que es 4 por 7 que se muestra a continuación. Su longitud es de 7 y su ancho es de 4.
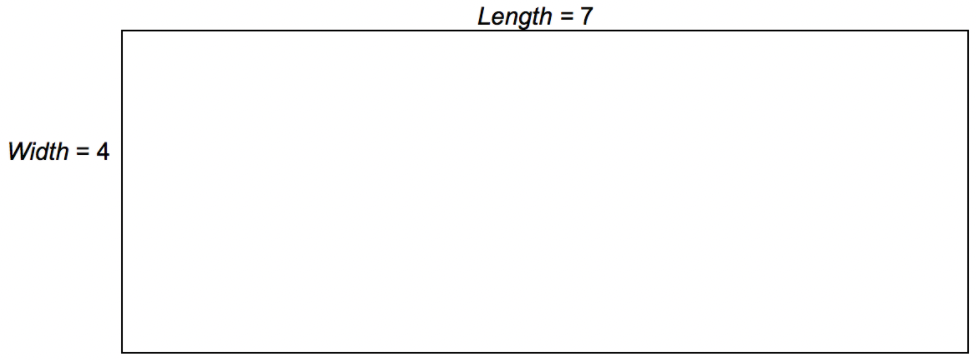
Se puede dividir el rectángulo en unidades haciendo 7 columnas y 4 filas.
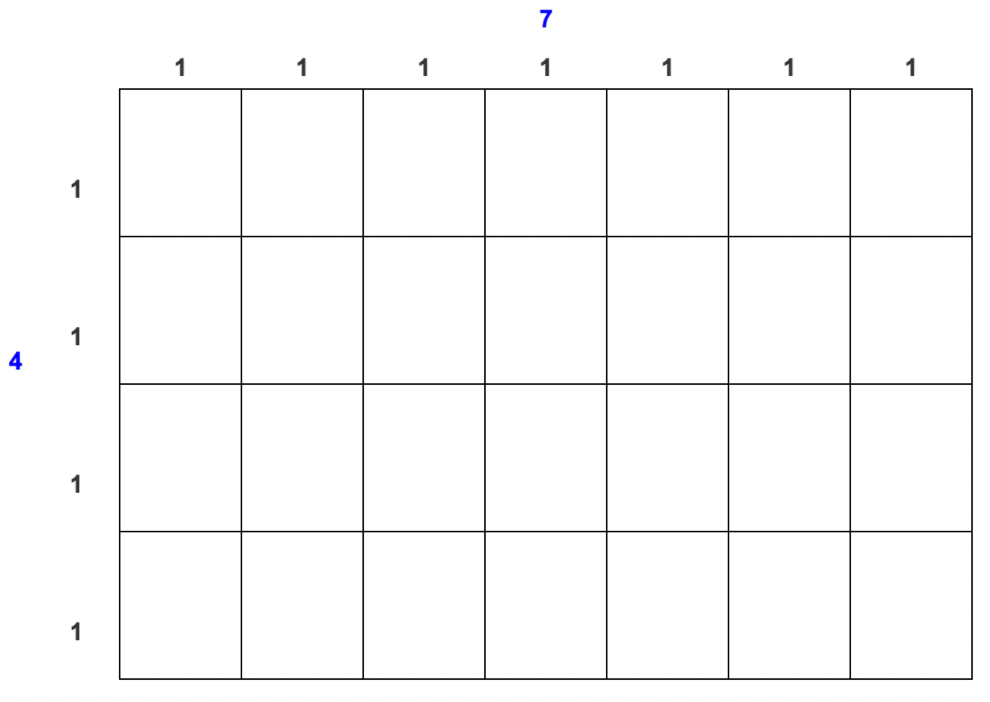
Se puede ver que dividir el rectángulo de esta manera resulta en 28 cuadrados. Se podría decir que el área del rectángulo es de 28 unidades cuadradas. También podrías encontrar el área multiplicando 7⋅4. (Nota: El área siempre se mide en unidades cuadradas: pulgadas cuadradas, centímetros cuadrados, pies cuadrados, etc.)
Considera un ejemplo de un rectángulo más grande, como el que se encuentra en un campo de fútbol. En cada extremo de un campo de fútbol, centrado en la portería, hay un rectángulo grande. A este rectángulo se le llama caja de penalti porque las faltas cometidas dentro de las líneas de este rectángulo pueden resultar en un tiro penal. En un campo de futbol reglamentario, el cuadro penal es de 44 yardas por 18 yardas. ¿Cuál es el área de una caja de penalti?
44 yards ⋅18 yards
Solución
\ (\\ begin {array} {r}
3\\\\\\
44\
\\ veces\ quad 18\
\ hline 352\\
+\ quad 440\
\ hline 792
\ end {array}\)
El área de la caja de penalti es de 792 yardas cuadradas.
¿Cuál es el área de un rectángulo cuya longitud es de 23 pies y cuyo ancho es de 7 pies?
- 30 pies
- 161 pies
- 161 pies cuadrados
- 1,421 pies cuadrados
- Contestar
-
- Incorrecto. Para encontrar el área, multiplicas, no agregas, el largo y ancho. La respuesta correcta es de 161 pies cuadrados.
- Incorrecto. El área se mide en unidades cuadradas. La respuesta correcta es de 161 pies cuadrados.
- Correcto. 23⋅7=161
- Incorrecto. Hay un error de valor-lugar. Cuando multiplicas 7⋅3, necesitas reagrupar 20 unos a 2 decenas y agregarlo al producto de 2 y 7. La respuesta correcta es de 161 pies cuadrados.
Uso de la multiplicación en la resolución de problemas
La multiplicación se utiliza para resolver muchos tipos de problemas. A continuación se presentan dos ejemplos que utilizan la multiplicación en sus soluciones al problema.
Un caso de comida para gatos tiene dos capas. Cada capa tiene 4 filas de 6 latas. ¿Cuántas latas hay en una caja de comida para gatos?
Solución
| \ (\\ begin {array} {r} 6\\ \ times\ quad 4\ \ hline 24 \ end {array}\) |
Primero encuentra el número de latas en una capa. Puedes multiplicar para averiguarlo. |
| \ (\\ begin {array} {r} 24\\ \ times\ quad 2\ \ hline 48 \ end {array}\) |
Dado que hay dos capas, multiplicas el número de latas en una capa por 2. |
Hay 48 latas en una caja de comida para gatos.
Un teatro tiene 45 filas con 40 asientos en cada fila. ¿Cuántos asientos hay en el teatro?
Solución
| \ (\\ begin {array} {rr} &&\ color {azul} 2\\\\\\ &&&45\ & &\ times\ quad &40\\ \ hline &&\ color {azul} 00\\ &\ color {azul} +\ quad&\ color { azul} 1800\\ \ hline &&\ color {azul} 1.800 \ end {array}\) |
Se puede resolver este problema sumando 40, 45 veces, pero eso tomaría mucho trabajo. La multiplicación es el camino a seguir. |
Hay mil 800 asientos en el teatro.
Una compañía de cuidado del césped cobra $35 por cortar un césped. Si la empresa corta 32 céspedes, ¿cuánto dinero ganará?
- $9,760
- 1,120
- $130.00
- $67.00
- Contestar
-
- Incorrecto. Esta respuesta es demasiado grande. Por estimación, 40⋅30=1200. Debe haber un error en el reagrupamiento o el valor posicionar. La respuesta correcta es $1,120.
- Correcto. 35⋅32=1,200
- Incorrecto. La respuesta debe ser un número mayor. Por estimación, 40⋅30=1200. Debe haber un error en el reagrupamiento o el valor posicionar. La respuesta correcta es $1,120.
- Incorrecto. Debes multiplicar, no sumar, 32 y 35. La respuesta correcta es $1,120.
Resumen
La multiplicación puede hacer que la adición repetida sea más fácil de calcular en cálculos y resolución de problemas. La multiplicación se puede escribir usando tres símbolos: paréntesis, un signo de tiempos o un punto de multiplicación. Para realizar la multiplicación con factores de dos dígitos o mayores, puede usar el algoritmo estándar donde multiplica cada uno de los números en cada factor por los números en el otro factor. El uso de estrategias como atajo para multiplicar por potencias de 10 y estimación para verificar tus respuestas puede facilitar la multiplicación así como reducir errores.


