1.3.2: Dividir números enteros y aplicaciones

Última actualización
Guardar como PDF

Page ID: 111167

The NROC Project

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

Utilice tres formas diferentes de representar la división.
Dividir números enteros.
Realizar división larga.
Divide números enteros por una potencia de 10.
Reconocer que la división por 0 no está definida.
Resolver problemas de aplicación usando división.

Introducción

Algunas personas piensan en la división como “reparto justo” porque cuando divides un número estás tratando de crear partes iguales. La división es también la operación inversa de la multiplicación porque “deshace” la multiplicación. En la multiplicación, se combinan conjuntos iguales para crear un total. En división, se separa un grupo entero en conjuntos que tienen la misma cantidad. Por ejemplo, podrías usar la división para determinar cómo compartir 40 empanadas entre 12 invitados en una fiesta.

¿Qué es la División?

La división se divide en partes iguales o grupos. Por ejemplo, se podría usar la división para determinar cómo compartir un plato de cookies de manera uniforme entre un grupo. Si hay 15 cookies para compartir entre cinco personas, podrías dividir 15 por 5 para encontrar la “parte justa” que obtendría cada persona. Considera la imagen de abajo.

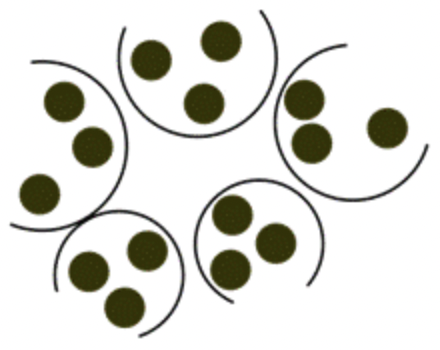
$Screen Shot 2021-04-12 en 3.49.51 PM.png$

15 galletas divididas uniformemente en 5 platos dan como resultado 3 galletas en cada plato. Se podría representar esta situación con la ecuación:

$\ 15 \div 5=3$

También podrías usar una línea numérica para modelar esta división. Así como se puede pensar en la multiplicación como suma repetida, se puede pensar en la división como resta repetida. Considera cuántos saltos tomas por 5s a medida que pasas de 15 atrás a 0 en la línea numérica.

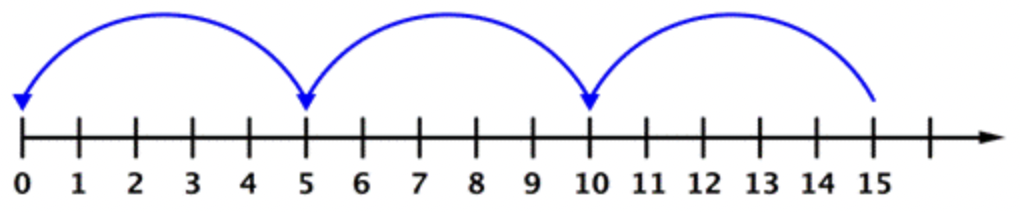
$Screen Shot 2021-04-12 en 3.51.46 PM.png$

Observe que hay 3 saltos que realiza cuando salta la cuenta por 5 de 15 de vuelta a 0 en la recta numérica. Esto es como restar 5 de 15 tres veces. Esta resta repetida puede ser representada por la ecuación:$\ 15 \div 5=3$.

Por último, considere cómo un modelo de área puede mostrar esta división. Pregúntate, si fueras a hacer un rectángulo que contuviera 15 cuadrados con 5 cuadrados seguidos, ¿cuántas filas habría en el rectángulo? Comienza haciendo una fila de 5 cuadrados:

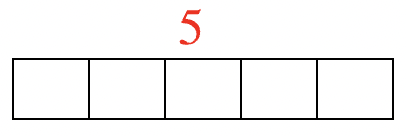
$Screen Shot 2021-04-12 en 3.56.19 PM.png$

Después agrega dos filas más de 5 cuadrados para que tengas 15 cuadrados.

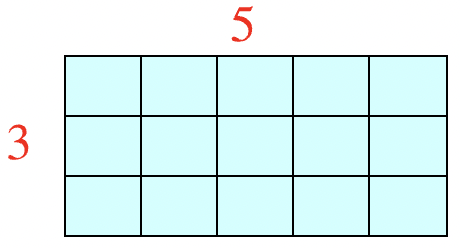
$Screen Shot 2021-04-12 en 3.57.02 PM.png$

El número de filas es 3. Entonces, 15 dividido por 5 es igual a 3.

Ejemplo

Buscar$\ 24 \div 3$ usando un modelo de conjunto y un modelo de línea numérica.

Solución

Modelo de conjunto:

$Screen Shot 2021-04-12 en 3.58.43 PM.png$

Modelo de línea numérica:

$Screen Shot 2021-04-12 en 3.59.12 PM.png$

$\ 24 \div 3=8$

Formas de representar la división

Al igual que con la multiplicación, la división se puede escribir usando algunos símbolos diferentes. Mostramos esta división escrita como$\ 15 \div 5=3$, pero también se puede escribir de otras dos maneras:

\ (\\ begin {array} {r}
3\\
5\ longdiv {1 5}
\ end {array}\)

$\ \frac{15}{5}=3$

Cada parte de un problema de división tiene un nombre. Al número que se está dividiendo, es decir el total, se le llama dividendo. En el trabajo en este tema, este número será el número mayor, pero eso no siempre es cierto en matemáticas. El número que está dividiendo el dividendo se llama divisor. La respuesta a un problema de división se llama cociente.

El cuadro azul a continuación resume la terminología y las formas comunes de representar la división.

Tres formas de representar la división

$\ 12 \div 3=4$(con un símbolo de división; esta ecuación se lee “12 dividido por 3 es igual a 4”.

\ (\\ begin {array} {r}
4\\
3\ longdiv {1 2}
\ end {array}\) (con un símbolo de división o división larga; esta expresión se lee “12 dividido por 3 es igual a 4”. Observe aquí, sin embargo, que hay que comenzar con lo que está debajo del símbolo. Esto puede tomar algún tiempo acostumbrarse ya que estás leyendo de derecha a izquierda y de abajo a arriba!)

$\ \frac{12}{3}=4$(con una barra de fracciones; esta expresión también se puede leer “12 dividido por 3 es igual a 4”. En este formato, lees de arriba a abajo.)

En los ejemplos anteriores, 12 es el dividendo, 3 es el divisor y 4 es el cociente.

$\ \text { Dividend } \div \text { Divisor }=\text { Quotient }$

\ (\\ begin {array} {r}
\ text {cociente}\
\ text {Divisor}\ longdiv {\ text {Dividendo}}
\ end {array}\)

$\ \frac{\text { Dividend }}{\text { Divisor }}=\text { Quotient }$

Ejercicio

¿Cuál de las siguientes expresiones representa dividir $56 por igual entre 7 personas?

#1:$\ \frac{7}{56}$

#2:$\ 56 \div 7$

#3:$\ 56\longdiv {7}$

#2 representa la situación.
Las tres expresiones representan la situación.
#1 representa la situación.
#3 representa la situación.

Contestar

Correcto. #2 es la única expresión que representa 56 dividido por 7.
Incorrecto. #1 y #3 representan 7 dividido por 56, no 56 dividido por 7. La respuesta correcta es #2 es la única expresión que representa la situación.
Incorrecto. Esta expresión representa 7 dividido por 56, no 56 dividido por 7. La respuesta correcta es #2 es la única expresión que representa la situación.
Incorrecto. Esta expresión representa 7 dividido por 56, no 56 dividido por 7. La respuesta correcta es #2 es la única expresión que representa la situación.

Dividiendo números enteros

Una vez que entiendas cómo se escribe la división, estás en camino de resolver problemas simples de división. Necesitarás tus datos de multiplicación para realizar la división. Si no los tienes memorizados, puedes adivinar y verificar o usar una calculadora.

Considere los siguientes problemas:

$\ 10 \div 5=?$

$\ 48 \div 2=?$

$\ 30 \div 5=?$

En el primer problema$\ 10 \div 5$,, podrías preguntarte, “¿cuántos cincos hay en diez?” Probablemente puedas responder esto fácilmente. Otra forma de pensar en esto es considerar dividir 10 en 5 grupos e imaginar cuántos serían en cada grupo.

$\ 10 \div 5=2$

Para resolver$\ 48 \div 2$, podrías darte cuenta de que dividir por 2 es como dividir en dos grupos o dividir el total por la mitad. ¿Qué número podrías duplicar para obtener 48?

$\ 48 \div 2=24$

Para averiguarlo$\ 30 \div 5$, podrías preguntarte, ¿cuántas veces tienes que saltarte la cuenta por 5 para llegar de 0 a 30? 5, 10, 15, 20, 25, 30. Tienes que saltarte el conteo 6 veces para llegar a 30.

$\ 30 \div 5=6$

Ejercicio

Cómputos$\ 35 \div 5$.

Contestar: 7

Ejercicio

Cómputos$\ 32 \div 4$.

Contestar: 8

A veces cuando estás dividiendo, no puedes compartir fácilmente el número por igual. Piensa en el problema de la división$\ 9 \div 2$. Se podría pensar en este problema como 9 trozos de chocolate que se dividen entre 2 personas. Podrías hacer dos grupos de 4 chocolates, y te sobraría un chocolate.

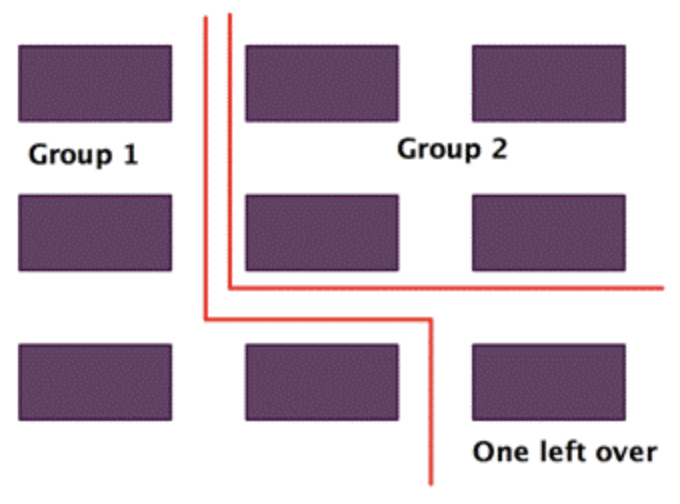
$Screen Shot 2021-04-14 a las 12.57.15 PM.png$

En matemáticas, esta parte sobrante se llama el resto. Es la parte que queda después de realizar la división. En el ejemplo anterior, el resto es 1. Podemos escribir esto como:

$\ 9 \div 2=4\quad \mathrm{R} 1$

Leemos esta ecuación: “Nueve dividido por dos equivale a cuatro con un resto de 1”.

Podrías estar pensando que podrías dividir ese trozo extra de chocolate en partes para compartirlo. ¡Esto es un gran pensamiento! Si divides el chocolate por la mitad, podrías darle a cada persona otra mitad de un trozo de chocolate. Cada uno obtendría$\ 4 \frac{1}{2}$ trozos de chocolate. No nos vamos a preocupar por expresar los restos como fracciones o decimales en estos momentos. Vamos a usar la notación del resto con la letra R. He aquí un ejemplo:

Ejemplo

$\ 45 \div 6$

Solución

$\ 6 \cdot 7=42$	¿Cuántos seis hay en 45? Prueba 7.
$\ 45-42=3$	3 no es suficiente para otro 6. Entonces, 3 es el resto.

$\ 45 \div 6=7\quad \mathrm{R} 3$

Dado que la multiplicación es la inversa de la división, puedes verificar tu respuesta a un problema de división con la multiplicación. Para verificar la respuesta 7 R3, primero multiplique 6 por 7 y luego agregue 3.

$\ 6 \cdot 7=42$

$\ 42+3=45$, por lo que el cociente 7 R3 es correcto.

Ejercicio

Cómputos$\ 67 \div 7$.

9
9 R4
60
10

Contestar

Incorrecto. $\ 9 \cdot 7=63$. Hay un resto de 4. La respuesta correcta es 9 R4.
Correcto. $\ 9 \cdot 7=63$y quedan 4.
Incorrecto. Esto es un problema de división, no resta. La respuesta correcta es 9 R4.
Incorrecto. $\ 70 \div 7=10$, entonces la respuesta a$\ 67 \div 7$ no puede ser;$\ 9 \cdot 7=63$ y quedan 4. La respuesta correcta es 9 R4.

Realización de División Larga

La división larga es un método que es útil cuando estás realizando una división que no puedes hacer fácilmente en tu cabeza, como la división que involucra números más grandes. A continuación se muestra un ejemplo de una manera de escribir los pasos de división.

Ejemplo

$\ 68 \div 4$

Solución

$\ 4 \longdiv { 6 8 }$	Reescribir la división.
\ (\\ begin {array} {r} 1\\ 4\ longdiv {68}\\ -4\\\\ \ hline 28 \ end {array}\)	Dividir las decenas. ¿Qué es 6 dividido por 4? $\ 4 \cdot 1=4$, así que escribe un 1 arriba del 6. Restar 4 de 6 y bajar el siguiente dígito del dividendo, 8. ¿Qué es 28 dividido por 4?
\ (\\ begin {array} {r} 17\\ 4\ longdiv {68}\\ -4\\\\ \ hline 28\\ -28\ \ hline 0 \ end {array}\)	$\ 7 \cdot 4=28$, así que escribe un 7 arriba del 8. No hay resto.
\ (\\ begin {array} {r} 17\ cdot 4\\ ^217\\ \ veces 4\\ \ hline 68 \ end {array}\)	Comprueba tu respuesta usando multiplicación.

$\ 68 \div 4=17$

Ejemplo

$\ 6,707 \div 233$

Solución

\ (\\ begin {array} {r} 2\\ 233\ longdiv {6707}\\ -466\\\\ \ hline \ end {array}\)	Examine los primeros 3 dígitos del dividendo y determine cuántos 233 hay en él. Usa guess and check. Prueba:$\ 2 \cdot 233=466$ Prueba:$\ 3 \cdot 233=699$ (demasiado grande)
\ (\\ begin {array} {r} 2\\ 233\ longdiv {6707}\\ -466\\\\ \ hline 2047\ \ end {array}\)	Restar 466 de 670 y bajar el siguiente dígito del dividendo, 7.
\ (\\ begin {array} {r} 28\\ 233\ longdiv {6707}\\ -466\\\ \ hline 2047\\\ -1864\\ \ hline 183\ \ end {array}\)	¿Cuántos 233 hay en 2,047? Parece cerca de 10 porque$\ 233 \cdot 10=2,330$. Intentar$\ 9.233 \cdot 9$ es igual a 2,097. \ (\\ begin {array} {r} 22\\\\ 233\ \ times\ quad 9\\ \ hline 2.097 \ end {array}\) 2,097 (Demasiado grande) ¡Deben ser 8! \ (\\ begin {array} {r} 22\\\\ 233\ \ times\ quad 8\\ \ hline 1,864 \ end {array}\)
$\ 233 \cdot 28=6,524$ $\ 6,524+183=6,707$	Comprueba tu respuesta usando multiplicación. Primero, multiplicar$\ 233 \cdot 28$. Después, agregue el resto.

$\ 6,707 \div 233=28 \quad\mathrm{R} 183$

Ejercicio

Cómputos$\ 417 \div 34$.

451
12
12 R9
13

Contestar

Incorrecto. Esto es un problema de división, no un problema de adición. La respuesta correcta es 12 R9.
Incorrecto. $\ 12 \cdot 34=408$. La respuesta correcta es 12 R9.
Correcto. $\ 12 \cdot 34=408$y$\ 408+9=417$
Incorrecto. $\ 13 \cdot 34=442$. La respuesta correcta es 12 R9.

Dividiendo números enteros por una potencia de 10

Así como la multiplicación por potencias de 10 da como resultado un patrón, hay un patrón con división por potencias de 10. Considerar tres cocientes:$\ 20 \div 10 ; 200 \div 10 ; 2,000 \div 10$.

Piense en$\ 20 \div 10$. Hay 2 decenas en veinte, entonces$\ 20 \div 10=2$. Los cálculos para$\ 200 \div 10$ y$\ 2,000 \div 10$ se muestran a continuación.

Ejemplo

$\ 200 \div 10$

Solución

$\ 1 0 \longdiv { 2 0 0 }$	Reescribe el problema.
$\ 1 0 \longdiv { {\color{red}2} {\color{blue}0} 0 }$	Dividir el primer dígito del dividendo, 2, por el divisor. Ya que$\ 2 \div 10$ no da un número entero, vaya al siguiente dígito, 0.
\ (\\ begin {array} {r} 2\\ 1 0\ longdiv {{\ color {rojo} 2 0} 0} \ end {array}\)	$\ 20 \div 10=2$
\ (\\ begin {array} {r} 2\\ 10\ longdiv {200}\\ -20\\\\ \ hline 0\\\ \ final {matriz}\\)	$\ 2 \cdot 10=20$ $\ 20-20=0$
\ (\\ begin {array} {r} 2\\ 10\ longdiv {20\ color {rojo} 0}\\ -20\\\ \ hline 0\\ color {rojo} 0\ \ end {array}\\)	Bajar el siguiente dígito del dividendo, que es 0.
\ (\\ begin {array} {r} 2\ color {azul} 0\\\ 10\ longdiv {200}\\ -20\\\\ hline 00\ \\\ hline 00\\\ 0\\ \ hline 0\ \ end {array}\)	Ya que 10 todavía no entra en 00 y no nos queda nada por derribar, multiplicar el 0 por 10. $\ 0 \cdot 10=0$ $\ 0-0=0$ No tenemos resto.

$\ 200 \div 10=20$

Ejemplo

$\ 2000 \div 10$

Solución

$\ 1 0 \longdiv { 2 0 0 0 }$	Reescribe el problema.
$\ 1 0 \longdiv { {\color{red}2} 0 0 0 }$	Dividir el primer dígito del dividendo, 2, por el divisor. Ya que$\ 2 \div 10$ no da un número entero, vaya al siguiente dígito, 0.
\ (\\ begin {array} {r} 2\\ 1 0\ longdiv {{\ color {rojo} 2 0} 0 0} \ end {array}\)	$\ 20 \div 10=2$
\ (\\ begin {array} {r} 2\\\ 10\ longdiv {2000}\\ -20\\\\\\ \ hline 0\\\\\\ \ fin {matriz}\\)	$\ 2 \cdot 10=20$ $\ 20-20=0$
\ (\\ begin {array} {r} 2\\ 10\ longdiv {20 {\ color {rojo} 0} 0}\\ -20\\\\\ \ hline 0\\ color {rojo} 0\\\ \ final {array}\\)	Bajar el siguiente dígito, 0, del dividendo.
\ (\\ begin {array} {r} 2\ color {azul} 0\\ 10\ longdiv {200\ color {rojo} 0}\\ -20\\\\\\ \ hline 00\ color {rojo} 0 \ end {array}\\)	Ya que 10 no entra en 00, suma un 0 al cociente y baja el siguiente dígito, 0.
\ (\\ begin {array} {r} 20\ color {azul} 0\\ 10\ longdiv {2000}\\ -20\\\\\\ \ hline 000\\\ 0\ \ hline 0 \ end {array}\)	Ya que 10 todavía no entra en 000 y no nos queda nada por derribar, sumar un 0 al cociente, multiplicar el 0 por 10. $\ 0 \cdot 10=0$ $\ 0-0=0$ No tenemos resto.

$\ 2,000 \div 10=200$

Examinar los resultados de estos tres problemas para tratar de determinar un patrón en división por 10.

\ (\\ begin {alineado}
20\ div 10 &=2\\
200\ div 10 &=20\\
2,000\ div 10 &=200
\ end {alineado}\)

Observe que el número de ceros en el cociente disminuye cuando un dividendo se divide por 10:20 se convierte en 2; 200 se convierte en 20 y 2,000 se convierte en 200. En cada uno de los ejemplos anteriores, se puede ver que hay un 0 menos en el cociente que en el dividendo.

Continuar otro ejemplo de división por una potencia de 10.

Ejemplo

$\ 2,000 \div 100$

Solución

$\ 1 0 0 \longdiv { 2 0 0 0 }$	Reescribe el problema.
$\ 1 0 0 \longdiv { {\color{red}2} 0 0 0 }$	Dividir el primer dígito del dividendo, 2, por el divisor. Ya que$\ 2 \div 100$ no da un número entero, vaya al siguiente dígito, 0.
$\ 1 0 0 \longdiv { {\color{red}2 0} 0 0 }$	Dividir los dos primeros dígitos del dividendo, 20, por el divisor. Ya que$\ 20 \div 100$ no da un número entero, vaya al siguiente dígito, 0.
$\ 1 0 0 \longdiv { {\color{red}2 0 0} 0 }$	$\ 200 \div 100=2$
\ (\\ begin {array} {r} 2\\ 100\ longdiv {2000}\\ -200\\\ \ hline 0\\\ \ fin {matriz}\\)	$\ 2 \cdot 100=200$ $\ 200-200=0$
\ (\\ begin {array} {r} 2\\ 100\ longdiv {200\ color {rojo} 0}\\ -200\\\\ \ hline 0\\ color {rojo} 0 \ end {array}\\)	Bajar el siguiente dígito, 0, del dividendo.
\ (\\ begin {array} {r} 2\ color {azul} 0\\\ 100\ longdiv {2000}\\ -200\\\ \ hline 00\\\ 0\ \ hline 0 \ end {array}\)	Ya que 100 todavía no entra en 00 y no nos queda nada por derribar, sumar un 0 al cociente, multiplicar el 0 por 10. $\ 0 \cdot 10=0$ $\ 0-0=0$ No tenemos resto.

$\ 2,000 \div 100=20$

Considera este conjunto de ejemplos de división por poderes de 10. ¿Qué patrón ves?

\ (\\ begin {array} {rl}
20 &\ div &10=2\\
200 &\ div &10=20\\
2,000 &\ div &10=200\\
2,000 &\ div &100=20\\
2,000 &\ div &1,000=2
\ end {array}\)

Observe que cuando divide un número por una potencia de 10, el cociente tiene menos ceros. Esto se debe a que la división por una potencia de 10 tiene un efecto sobre el valor posicional. Por ejemplo, al realizar la división$\ 18,000 \div 100=180$, el cociente, 180, tiene dos ceros menos que el dividendo, 18,000. Esto se debe a que la potencia de 10 divisor, 100, tiene dos ceros.

Ejercicio

Cómputos$\ 135,000 \div 100$.

13,500
134,900
13,500,000
1,350

Contestar

Incorrecto. Esta respuesta es demasiado grande. $\ 13,500 \cdot 100=1,350,000$. La respuesta correcta es 1,350.
Incorrecto. Esto es un problema de división, no de resta. La respuesta correcta es 1,350.
Incorrecto. Esto es un problema de división, no de multiplicación. La respuesta correcta es 1,350.
Correcto. 1,350\ cdot 100=135,000.

División por Cero

Sabes lo que significa dividir por 2 o dividir por 10, pero ¿qué significa dividir una cantidad por 0? ¿Es esto incluso posible? ¿Se puede dividir 0 por un número? Considera los dos problemas que se escriben a continuación.

$\ \frac{0}{8} \text { and } \frac{8}{0}$

Podemos leer la primera expresión, “cero dividido por ocho” y la segunda expresión, “ocho dividido por cero”. Dado que la multiplicación es la inversa de la división, podríamos reescribirlas como problemas de multiplicación.

$\ 0 \div 8=?$

$\ ? \cdot 8=0$

El cociente debe ser 0 porque$\ 0 \cdot 8=0$.

$\ \frac{0}{8}=0$

Ahora consideremos$\ \frac{8}{0}$.

$\ 8 \div 0=?$

$\ ? \cdot 0=8$

Esto no es posible. No hay número que pudieras multiplicar por cero y obtener ocho. Cualquier número multiplicado por cero es siempre cero. No hay cociente para$\ \frac{8}{0}$. No hay cociente para ningún número cuando se divide por cero.

La división por cero es una operación para la que no se puede encontrar respuesta, por lo que no está permitida. Decimos que la división por 0 es indefinida.

Uso de la división en la resolución de problemas

La división se utiliza para resolver muchos tipos de problemas. A continuación se presentan tres ejemplos de la vida real que utilizan la división en sus soluciones.

Ejemplo

Luana hizo 40 empanadas para una fiesta. Si las empanadas se dividen en partes iguales entre 12 invitados, ¿cuántos tendrá cada invitado? ¿Habrá alguna empanada sobrante?

Solución

$\ 40 \div 12$

Dado que cada invitado tendrá una participación igual, podemos usar la división.

\ (\\ begin {array} {r}
3\\
12\ longdiv {40}\\
-36\
\ hline
4
\ end {array}\)

Utilice prueba y error. Prueba 3.

$\ 12 \cdot 3=36$

Cuando 40 empanadas se dividen por igual entre 12 personas, quedan 4 sobrantes.

Cada invitado tendrá 3 empanadas. Quedarán 4 empanadas sobrantes.

Ejemplo

Una caja de baldosas tiene 12 cajas en ella. El caso cuesta 384 dólares. ¿Cuánto cuesta una caja?

Solución

$\ 384 \div 12$	Dado que las cajas cuestan cada una la misma cantidad, se quiere dividir $384 en 12 partes iguales.
\ (\\ begin {array} {r} 12\ longdiv {384} \ end {array}\)	Realizar la división. Trate de dividir el primer dígito del dividendo por el divisor. 12 no se dividirá en 3, así que vaya al siguiente dígito.
\ (\\ begin {array} {r} 3\\ 12\ longdiv {384}\\ -36\\\\ \ hline \ end {array}\)	Realizar$\ 38 \div 12$. Escoge un cociente y pruébalo. Prueba 3. $\ 3 \cdot 12=36$.
\ (\\ begin {array} {r} 3\\ 12\ longdiv {384}\\ -36\\\\ \ hline 2\\\ \ fin {matriz}\\)	Restar 36 de 38.
\ (\\ begin {array} {r} 32\\ 12\ longdiv {384}\\ -36\\\\ \ hline 24\\ -24\ \ hline 0 \ end {array}\)	Baja el siguiente dígito del dividendo y realiza la división. $\ 12 \cdot 2=24$ $\ 24-24=0$
\ (\\ begin {array} {r} 32\\ \ times\ quad 12\ \\ hline 64\\ +\ quad320\ \ hline 384 \ end {array}\)	¿$\ 32 \cdot 12$Equivale 384? Comprueba tu respuesta multiplicando. ¡Sí! ¡La respuesta es correcta!

Cada caja de azulejos cuesta $32

Ejemplo

Un productor de banano envía 4,644 plátanos. Hay 86 cajas, cada una con el mismo número de plátanos. ¿Cuántos plátanos hay en cada caja?

Solución

$\ 4,644 \div 86$	Dado que cada caja, o caja, tiene el mismo número de plátanos, puede tomar el número total de plátanos y dividirlo por el número de cajas. Reescribir la división.
$\ 8 6 \longdiv { 4 6 4 4 }$	Utilice prueba y error para determinar lo que$\ 464 \div 86$ es igual. Prueba 5: \ (\\ begin {array} {r} ^386\\ \ times\ quad 5\ \ hline 430 \ end {array}\)
\ (\\ begin {array} {r} 5\\ 86\ longdiv {4644}\\ -430\\\\ \ hline 344\ \ end {array}\)	$\ 464-430=34$ Entonces, baje el siguiente dígito del dividendo, 4.
\ (\\ comenzar {matriz} {r} 54\\ 86\ longdiv {4644}\\ -430\\\ \ hline 344\\ -344\ \ hline 0 \ end {array}\)	Utilice ensayo y error para determinar el cociente de 344 y 86. Prueba 4: \ (\\ begin {array} {r} ^286\ \\ veces 4\ \ hline 344 \ end {array}\)
\ (\\ begin {array} {r} 86\ \\ veces 54\ \ hline 344\\ +4300\ \ hline 4644 \ end {array}\)	Comprueba tu respuesta multiplicando. ¡Sí! ¡La respuesta es correcta!

Cada caja contiene 54 plátanos.

Ejercicio

Un teatro tiene 1,440 asientos. El teatro tiene 30 filas de asientos. ¿Cuántos asientos hay en cada fila?

1,410
48
43,200
480

Contestar

Incorrecto. Esta respuesta es demasiado grande. Use división,$\ 1440 \div 30$, no resta para este problema. La respuesta correcta es 48.
Correcto. $\ 1440 \div 30=48$.
Incorrecto. La respuesta es demasiado grande. Usa la división,$\ 1440 \div 30$, no la multiplicación, para este problema. La respuesta correcta es 48.
Incorrecto. Hay un error de valor de lugar. La respuesta correcta es 48.

Resumen

La división es la operación inversa de multiplicación, y se puede utilizar para determinar cómo compartir uniformemente una cantidad entre un grupo. La división se puede escribir de tres maneras diferentes: usando una barra de fracciones, usando un símbolo de división y usando división larga. La división se puede representar como dividir una cantidad total en conjuntos de cantidades iguales, como omitir restar en la recta numérica y como una dimensión con un modelo de área. Los restos pueden resultar al realizar la división y se pueden representar con la letra R, seguido del número restante. Dado que la división es la operación inversa de la multiplicación, necesitas conocer tus hechos de multiplicación para poder hacer división. Para números más grandes, puede usar la división larga para encontrar el cociente.

\(\ 1 0 0 \longdiv { 2 0 0 0 }\)	Reescribe el problema.
\(\ 1 0 0 \longdiv { {\color{red}2} 0 0 0 }\)	Dividir el primer dígito del dividendo, 2, por el divisor. Ya que\(\ 2 \div 100\) no da un número entero, vaya al siguiente dígito, 0.
\(\ 1 0 0 \longdiv { {\color{red}2 0} 0 0 }\)	Dividir los dos primeros dígitos del dividendo, 20, por el divisor. Ya que\(\ 20 \div 100\) no da un número entero, vaya al siguiente dígito, 0.
\(\ 1 0 0 \longdiv { {\color{red}2 0 0} 0 }\)	\(\ 200 \div 100=2\)
\ (\\ begin {array} {r} 2\\ 100\ longdiv {2000}\\ -200\\\ \ hline 0\\\ \ fin {matriz}\\)	\(\ 2 \cdot 100=200\) \(\ 200-200=0\)
\ (\\ begin {array} {r} 2\\ 100\ longdiv {200\ color {rojo} 0}\\ -200\\\\ \ hline 0\\ color {rojo} 0 \ end {array}\\)	Bajar el siguiente dígito, 0, del dividendo.
\ (\\ begin {array} {r} 2\ color {azul} 0\\\ 100\ longdiv {2000}\\ -200\\\ \ hline 00\\\ 0\ \ hline 0 \ end {array}\)	Ya que 100 todavía no entra en 00 y no nos queda nada por derribar, sumar un 0 al cociente, multiplicar el 0 por 10. \(\ 0 \cdot 10=0\) \(\ 0-0=0\) No tenemos resto.

\(\ 6 \cdot 7=42\)	¿Cuántos seis hay en 45? Prueba 7.
\(\ 45-42=3\)	3 no es suficiente para otro 6. Entonces, 3 es el resto.

\(\ 4 \longdiv { 6 8 }\)	Reescribir la división.
\ (\\ begin {array} {r} 1\\ 4\ longdiv {68}\\ -4\\\\ \ hline 28 \ end {array}\)	Dividir las decenas. ¿Qué es 6 dividido por 4? \(\ 4 \cdot 1=4\), así que escribe un 1 arriba del 6. Restar 4 de 6 y bajar el siguiente dígito del dividendo, 8. ¿Qué es 28 dividido por 4?
\ (\\ begin {array} {r} 17\\ 4\ longdiv {68}\\ -4\\\\ \ hline 28\\ -28\ \ hline 0 \ end {array}\)	\(\ 7 \cdot 4=28\), así que escribe un 7 arriba del 8. No hay resto.
\ (\\ begin {array} {r} 17\ cdot 4\\ ^217\\ \ veces 4\\ \ hline 68 \ end {array}\)	Comprueba tu respuesta usando multiplicación.

\(\ 1 0 \longdiv { 2 0 0 }\)	Reescribe el problema.
\(\ 1 0 \longdiv { {\color{red}2} {\color{blue}0} 0 }\)	Dividir el primer dígito del dividendo, 2, por el divisor. Ya que\(\ 2 \div 10\) no da un número entero, vaya al siguiente dígito, 0.
\ (\\ begin {array} {r} 2\\ 1 0\ longdiv {{\ color {rojo} 2 0} 0} \ end {array}\)	\(\ 20 \div 10=2\)
\ (\\ begin {array} {r} 2\\ 10\ longdiv {200}\\ -20\\\\ \ hline 0\\\ \ final {matriz}\\)	\(\ 2 \cdot 10=20\) \(\ 20-20=0\)
\ (\\ begin {array} {r} 2\\ 10\ longdiv {20\ color {rojo} 0}\\ -20\\\ \ hline 0\\ color {rojo} 0\ \ end {array}\\)	Bajar el siguiente dígito del dividendo, que es 0.
\ (\\ begin {array} {r} 2\ color {azul} 0\\\ 10\ longdiv {200}\\ -20\\\\ hline 00\ \\\ hline 00\\\ 0\\ \ hline 0\ \ end {array}\)	Ya que 10 todavía no entra en 00 y no nos queda nada por derribar, multiplicar el 0 por 10. \(\ 0 \cdot 10=0\) \(\ 0-0=0\) No tenemos resto.

\(\ 1 0 \longdiv { 2 0 0 0 }\)	Reescribe el problema.
\(\ 1 0 \longdiv { {\color{red}2} 0 0 0 }\)	Dividir el primer dígito del dividendo, 2, por el divisor. Ya que\(\ 2 \div 10\) no da un número entero, vaya al siguiente dígito, 0.
\ (\\ begin {array} {r} 2\\ 1 0\ longdiv {{\ color {rojo} 2 0} 0 0} \ end {array}\)	\(\ 20 \div 10=2\)
\ (\\ begin {array} {r} 2\\\ 10\ longdiv {2000}\\ -20\\\\\\ \ hline 0\\\\\\ \ fin {matriz}\\)	\(\ 2 \cdot 10=20\) \(\ 20-20=0\)
\ (\\ begin {array} {r} 2\\ 10\ longdiv {20 {\ color {rojo} 0} 0}\\ -20\\\\\ \ hline 0\\ color {rojo} 0\\\ \ final {array}\\)	Bajar el siguiente dígito, 0, del dividendo.
\ (\\ begin {array} {r} 2\ color {azul} 0\\ 10\ longdiv {200\ color {rojo} 0}\\ -20\\\\\\ \ hline 00\ color {rojo} 0 \ end {array}\\)	Ya que 10 no entra en 00, suma un 0 al cociente y baja el siguiente dígito, 0.
\ (\\ begin {array} {r} 20\ color {azul} 0\\ 10\ longdiv {2000}\\ -20\\\\\\ \ hline 000\\\ 0\ \ hline 0 \ end {array}\)	Ya que 10 todavía no entra en 000 y no nos queda nada por derribar, sumar un 0 al cociente, multiplicar el 0 por 10. \(\ 0 \cdot 10=0\) \(\ 0-0=0\) No tenemos resto.

\(\ 384 \div 12\)	Dado que las cajas cuestan cada una la misma cantidad, se quiere dividir $384 en 12 partes iguales.
\ (\\ begin {array} {r} 12\ longdiv {384} \ end {array}\)	Realizar la división. Trate de dividir el primer dígito del dividendo por el divisor. 12 no se dividirá en 3, así que vaya al siguiente dígito.
\ (\\ begin {array} {r} 3\\ 12\ longdiv {384}\\ -36\\\\ \ hline \ end {array}\)	Realizar\(\ 38 \div 12\). Escoge un cociente y pruébalo. Prueba 3. \(\ 3 \cdot 12=36\).
\ (\\ begin {array} {r} 3\\ 12\ longdiv {384}\\ -36\\\\ \ hline 2\\\ \ fin {matriz}\\)	Restar 36 de 38.
\ (\\ begin {array} {r} 32\\ 12\ longdiv {384}\\ -36\\\\ \ hline 24\\ -24\ \ hline 0 \ end {array}\)	Baja el siguiente dígito del dividendo y realiza la división. \(\ 12 \cdot 2=24\) \(\ 24-24=0\)
\ (\\ begin {array} {r} 32\\ \ times\ quad 12\ \\ hline 64\\ +\ quad320\ \ hline 384 \ end {array}\)	¿\(\ 32 \cdot 12\)Equivale 384? Comprueba tu respuesta multiplicando. ¡Sí! ¡La respuesta es correcta!

\(\ 4,644 \div 86\)	Dado que cada caja, o caja, tiene el mismo número de plátanos, puede tomar el número total de plátanos y dividirlo por el número de cajas. Reescribir la división.
\(\ 8 6 \longdiv { 4 6 4 4 }\)	Utilice prueba y error para determinar lo que\(\ 464 \div 86\) es igual. Prueba 5: \ (\\ begin {array} {r} ^386\\ \ times\ quad 5\ \ hline 430 \ end {array}\)
\ (\\ begin {array} {r} 5\\ 86\ longdiv {4644}\\ -430\\\\ \ hline 344\ \ end {array}\)	\(\ 464-430=34\) Entonces, baje el siguiente dígito del dividendo, 4.
\ (\\ comenzar {matriz} {r} 54\\ 86\ longdiv {4644}\\ -430\\\ \ hline 344\\ -344\ \ hline 0 \ end {array}\)	Utilice ensayo y error para determinar el cociente de 344 y 86. Prueba 4: \ (\\ begin {array} {r} ^286\ \\ veces 4\ \ hline 344 \ end {array}\)
\ (\\ begin {array} {r} 86\ \\ veces 54\ \ hline 344\\ +4300\ \ hline 4644 \ end {array}\)	Comprueba tu respuesta multiplicando. ¡Sí! ¡La respuesta es correcta!