1.4.1: Propiedades y leyes de los números enteros
- Page ID
- 111152
- Simplifique mediante el uso de la propiedad de suma de 0.
- Simplifica usando la propiedad de multiplicación de 1.
- Identificar y utilizar la ley conmutativa de adición.
- Identificar y utilizar la ley conmutativa de la multiplicación.
- Identificar y utilizar la ley asociativa de adición.
- Identificar y utilizar la ley asociativa de la multiplicación.
Introducción
Las matemáticas a menudo implican simplificar las expresiones numéricas. Al hacerlo, puede usar leyes y propiedades que se aplican a operaciones particulares. La propiedad de multiplicación de 1 establece que cualquier número multiplicado por 1 es igual al mismo número, y la propiedad de suma de cero establece que cualquier número agregado a cero es el mismo número.
Dos leyes importantes son las leyes conmutativas, que establecen que el orden en que se suman dos números o se multiplican dos números no afecta la respuesta. Puedes recordar esto porque si viajas al trabajo vas a la misma distancia conduciendo al trabajo y conduciendo a casa que conduces a casa y conduces al trabajo. Se pueden mover números alrededor además de expresiones de suma y multiplicación porque el orden en estas expresiones no importa.
También aprenderás a simplificar las expresiones de suma y multiplicación utilizando las leyes asociativas. Al igual que con las leyes conmutativas, existen leyes asociativas para la suma y la multiplicación. Al igual que las personas pueden asociarse con personas en diferentes grupos, un número puede asociarse con otros números en un grupo u otro. Las leyes asociativas permiten colocar números en diferentes grupos usando paréntesis.
Propiedades de Adición y Multiplicación de 0 y 1
La propiedad de suma de 0 establece que para cualquier número que se agregue a 0, la suma es igual a ese número. Recuerda que no terminas con cero como respuesta; eso solo ocurre cuando te multiplicas. Tu respuesta es simplemente la misma que tu número original.
\(\ 62+0=?\)
Solución
| \(\ 62+0=62\) | Agregar cero a 62 no agrega ninguna cantidad a la suma, por lo que el número permanece 62. |
\(\ 62+0=62\)
\(\ 112+0=?\)
- 112
- 0
- 1
- 1,120
- Contestar
-
- Correcto. Agregar cero a un número no cambia un número.
- Incorrecto. Tu respuesta sería cero si multiplicas 112 por 0, pero no si agregas 112 a 0. La respuesta correcta es 112.
- Incorrecto. Agregar 112 a 0 no equivale a 1. La respuesta correcta es 112.
- Incorrecto. No pones cero en el lugar de unos y mueve otros dígitos hacia arriba por un valor posicional. Esto sólo ocurre si estás multiplicando un número por diez. La respuesta correcta es 112.
De acuerdo con la propiedad de multiplicación de 1, el producto de 1 y cualquier número da como resultado ese número. La respuesta es simplemente idéntica al número original.
\(\ 2,500 \cdot 1=?\)
Solución
| \(\ 2,500 \cdot 1=2,500\) | Al multiplicar 2,500 por 1 se obtiene el mismo número. |
\(\ 2,500 \cdot 1=2,500\)
\(\ 72,540 \cdot 1=?\)
- 725,401
- 72,541
- 72,540
- 72,539
- Contestar
-
- Incorrecto. No pones 1 en el lugar de unos y mueves otros dígitos hacia arriba por un valor posicionar. La respuesta correcta es 72,540.
- Incorrecto. No se agrega uno al número. La respuesta correcta es 72,540.
- Correcto. Al multiplicar cualquier número por 1 se obtiene el mismo número, que es en este caso 72,540.
- Incorrecto. No restas uno del número. La respuesta correcta es 72,540.
La Ley Conmutativa de la Adición
La ley conmutativa de la suma establece que se puede cambiar la posición de los números en una expresión de suma sin cambiar la suma. Por ejemplo, 3+2 es lo mismo que 2+3.
3+2=5
2+3=5
Es probable que encuentres rutinas diarias en las que se puede cambiar el orden. Por ejemplo, cuando te preparas para trabajar por la mañana, ponerte el guante izquierdo y el guante derecho es conmutativo. Podrías ponerte el guante derecho antes que el guante izquierdo, o el guante izquierdo antes del guante derecho. De igual manera, cepillarse los dientes y peinarse el cabello es conmutativo, porque no importa cuál haga primero.
Recuerda que esta ley sólo se aplica a la suma, y no a la resta. Por ejemplo:
8-2 no es lo mismo que 2-8.
A continuación, encontrarás ejemplos de expresiones que han sido cambiadas con la ley conmutativa. Tenga en cuenta que las expresiones que implican sustracción no se pueden cambiar.
| Expresión Original | Expresión reescrita |
| 4+5 | 5+4 |
| 6+728 | 728+6 |
| 9+4+1 | 9+1+4 |
| 9-1 | no se puede cambiar |
| 72-10 | no se puede cambiar |
| 128-100 | no se puede cambiar |
También es probable que te encuentres con rutinas de la vida real que no son conmutativas. A la hora de prepararnos para ir a trabajar, tiene que ocurrir ponernos la ropa antes de ponernos un abrigo. De igual manera, el meterse en el auto tiene que ocurrir antes de poner la llave en el encendido. En una tienda, tendrías que recoger los artículos que estás comprando antes de proceder a la caja registradora para pagar.
Escribe la expresión 10+25 de una manera diferente, usando la ley conmutativa de suma, y muestra que ambas expresiones dan como resultado la misma respuesta.
Solución
| 10+25=35 | Resolver el problema arroja una respuesta de 35. |
| 25+10 | Usando la propiedad conmutativa, se puede cambiar el 10 y el 25 para que estén en diferentes posiciones. |
| 25+10=35 | Al sumar 25 a 10 en este nuevo orden también se obtienen 35. |
10+25=35 y 25+10=35
Reescribir 15+12=27 de una manera diferente, utilizando la ley conmutativa de la adición.
- 15=12+27
- 12=15+27
- 15+ (12=27)
- 12+15=27
- Contestar
-
- Incorrecto. Solo puede cambiar el orden de los números a agregar. La respuesta correcta es 12+15=27.
- Incorrecto. Solo puede cambiar el orden de los números a agregar. La respuesta correcta es 12+15=27.
- Incorrecto. Nunca pondrías paréntesis alrededor de un signo = (y los paréntesis no se usan con las leyes conmutativas). La respuesta correcta es 12+15=27.
- Correcto. La ley conmutativa permite cambiar el orden de los números que se van a sumar.
La Ley Conmutativa de la Multiplicación
La multiplicación también tiene una ley conmutativa. La ley conmutativa de la multiplicación establece que cuando se multiplican dos o más números, se puede cambiar su orden sin afectar la respuesta. En el siguiente ejemplo, tenga en cuenta que 5 multiplicado por 4 arroja el mismo resultado que 4 multiplicado por 5. En ambos casos, la respuesta es 20.
\(\ 5 \cdot 4=20\)
\(\ 4 \cdot 5=20\)
Este ejemplo muestra cómo se pueden cambiar los números en una expresión de multiplicación.
Escribir la expresión de una\(\ 30 \cdot 50\) manera diferente, utilizando la ley conmutativa de la multiplicación, y mostrar que ambas expresiones dan como resultado la misma respuesta.
Solución
| \(\ 30 \cdot 50=1,500\) | Resolver el problema arroja una respuesta de 1,500. |
| \(\ 50 \cdot 30\) | Utilizando la ley conmutativa, se puede cambiar el 30 y el 50 para que estén en diferentes posiciones. |
| \(\ 50 \cdot 30=1,500\) | Multiplicando 50 y 30 también rinde 1,500. |
\(\ 50 \cdot 30\)y\(\ 30 \cdot 50=1,500\)
Ten en cuenta que cuando estás usando la ley conmutativa, solo se ve afectada la orden. El agrupamiento permanece sin cambios.
Reescribir\(\ 52 \cdot 46\) de una manera diferente, utilizando la ley conmutativa de la multiplicación.
- \(\ 42 \cdot 56\)
- \(\ 5 \cdot 246\)
- \(\ 5 \cdot 24 \cdot 6\)
- \(\ 46 \cdot 52\)
- Contestar
-
- Incorrecto. No se puede cambiar un dígito de cada número. La respuesta correcta es\(\ 46 \cdot 52\).
- Incorrecto. Deberían multiplicarse los mismos dos números. No se deben cambiar los números en sí, solo el orden en que aparecen los números. La respuesta correcta es\(\ 46 \cdot 52\).
- Incorrecto. Deberían multiplicarse los mismos dos números. No se deben cambiar los números en sí, solo el orden en que aparecen los números. La respuesta correcta es\(\ 46 \cdot 52\).
- Correcto. Se invierte el orden de los números, y se multiplican los mismos dos números.
La Ley Asociativa de la Adición
A continuación se presentan dos formas de simplificar y resolver un problema de adición. Tenga en cuenta que puede agregar números en cualquier orden. En el primer ejemplo, se agrega 4 a 5 para hacer 9.
4+5+6=9+6=15
Aquí, se resuelve el mismo problema, pero esta vez, se agrega 5 a 6 para hacer 11. Tenga en cuenta que resolverlo de esta manera arroja la misma respuesta.
4+5+6=4+11=15
La ley asociativa de adición establece que los números en una expresión de adición pueden reagruparse usando paréntesis. Puedes recordar el significado de la ley asociativa recordando que cuando te asocias con familiares, amigos y compañeros de trabajo, terminas formando grupos con ellos. En la siguiente expresión, se utilizan paréntesis para agrupar números para que sepas qué agregar primero. Tenga en cuenta que cuando los paréntesis están presentes, cualquier número entre paréntesis son números que agregará primero. La expresión puede ser reescrita con diferentes grupos utilizando la ley asociativa.
(4+5) +6=9+6=15
4+ (5+6) =4+11=15
Aquí, es claro que los paréntesis no afectan la respuesta final. La respuesta es la misma independientemente de dónde estén los paréntesis.
Reescribir (5+8) +3 usando la ley asociativa de adición. Mostrar que la expresión reescrita da la misma respuesta.
Solución
| (5+8) +3=13+3=16 | La expresión original arroja una respuesta de 16. |
| 5+ (8+3) =5+11=16 | Agrupar 8 y 3 en lugar de 5 y 8 da como resultado la misma respuesta de 16. |
(5+8) +3=16 y 5+ (8+3) =16
Al reescribir una expresión usando la ley asociativa, recuerda que estás reagrupando los números y no invirtiendo el orden, como en la ley conmutativa.
Reescribe 10+ (5+6) usando la propiedad asociativa.
- (5+6) +10
- 10+ (6+5)
- (10+5) +6
- (10+6) +5
- Contestar
-
- Incorrecto. El orden de los números no se cambia cuando se está reescribiendo la expresión utilizando la ley asociativa de adición. La forma en que se agrupan los números debería cambiar. La respuesta correcta es (10+5) +6.
- Incorrecto. El orden de los números no se cambia cuando se está reescribiendo la expresión utilizando la ley asociativa de adición. La forma en que se agrupan los números debería cambiar. La respuesta correcta es (10+5) +6.
- Correcto. Aquí, los números se reagrupan. Ahora 10 y 5 se agrupan entre paréntesis en lugar de 5 y 6.
- Incorrecto. El orden de los números no se cambia cuando se está reescribiendo la expresión utilizando la ley asociativa de adición. Sólo se debe cambiar la forma en que se agrupan los números. La respuesta correcta es (10+5) +6.
La Ley Asociativa de la Multiplicación
La multiplicación tiene una ley asociativa que funciona exactamente igual que la de suma. La ley asociativa de multiplicación establece que los números en una expresión de multiplicación pueden reagruparse usando paréntesis. La siguiente expresión se puede reescribir de una manera diferente utilizando la ley asociativa.
\(\ (2 \cdot 3) \cdot 4=2 \cdot(3 \cdot 4)\)
Aquí, es claro que los paréntesis no afectan la respuesta final. La respuesta es la misma independientemente de dónde estén los paréntesis.
Reescribir\(\ (10 \cdot 200) \cdot 24\) usando la ley asociativa de multiplicación, y mostrar que la expresión reescrita da la misma respuesta.
Solución
| \(\ (10 \cdot 200) \cdot 24=2000 \cdot 24=48,000\) | La expresión original arroja una respuesta de 48,000. |
| \(\ 10 \cdot(200 \cdot 24)=10 \cdot 4800=48,000\) | Agrupar 200 y 24 en lugar de 10 y 200 da como resultado la misma respuesta de 48 mil. |
\(\ (10 \cdot 200) \cdot 24=48,000\)y\(\ 10 \cdot(200 \cdot 24)=48,000\)
Al reescribir una expresión usando la ley asociativa, recuerda que estás reagrupando los números y no cambiando el orden. Cambiar el orden utiliza la ley conmutativa.
Reescribir\(\ 8 \cdot(7 \cdot 6)\) usando la propiedad asociativa.
- \(\ (8 \cdot 7) \cdot 6\)
- \(\ (7 \cdot 6) \cdot 8\)
- \(\ (7 \cdot 8) \cdot 6\)
- \(\ (8 \cdot 76)\)
- Contestar
-
- Correcto. Aquí, los números se reagrupan. Ahora 8 y 7 se agrupan entre paréntesis en lugar de 7 y 6.
- Incorrecto. El orden de los números no se cambia cuando se está reescribiendo la expresión utilizando la ley asociativa de multiplicación. La forma en que se agrupan debe cambiar. La respuesta correcta es\(\ (8 \cdot 7) \cdot 6\).
- Incorrecto. El orden de los números no se cambia cuando se está reescribiendo la expresión utilizando la ley asociativa de multiplicación. Sólo la forma en que se agrupan debe cambiar. La respuesta correcta es\(\ (8 \cdot 7) \cdot 6\).
- Incorrecto. Los dígitos de diferentes números no se combinan para crear nuevos números. La forma en que se agrupan los números debería cambiar. La respuesta correcta es\(\ (8 \cdot 7) \cdot 6\).
¿Conmutativo o Asociativo?
Cuando se está reescribiendo una expresión, se puede decir si se está reescribiendo usando las leyes conmutativas o asociativas en función de si cambia el orden de los números o los números se están reagrupando usando paréntesis.
Si se reescribe una expresión para que se cambie el orden de los números, se está utilizando la ley conmutativa.
\(\ 10 \cdot 2=20\)se reescribe como 2\(\ \cdot 10=20\). ¿Se reescribió esta expresión usando la ley conmutativa o la ley asociativa?
Solución
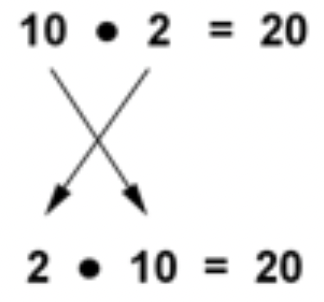Reescribir la expresión implica cambiar el orden de los números. Por lo tanto, se está utilizando la ley conmutativa.
Se está utilizando la ley conmutativa para reescribir la expresión.
Recuerda que cuando te asocias con amigos y familiares, normalmente te estás agrupando con otras personas. Entonces, si los números en una expresión se reagrupan usando paréntesis y el orden de los números sigue siendo el mismo, entonces se está utilizando la ley asociativa.
\(\ 2 \cdot(4 \cdot 6)=48\)se reescribe como\(\ (2 \cdot 4) \cdot 6=48\). ¿Se reescribió esta expresión usando la ley conmutativa o la ley asociativa?
Solución
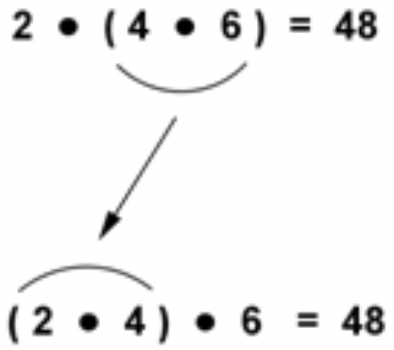Reagrupar usando paréntesis no cambia el orden de los números. Por lo tanto, se está utilizando la ley asociativa.
Se está utilizando la ley asociativa para reescribir la expresión.
\(\ 12 \cdot(6 \cdot 2)=144\)se reescribe como\(\ 3 \cdot 17=51\). ¿Se reescribió esta expresión usando la ley conmutativa o la ley asociativa?
- derecho conmutativo
- derecho asociativo
- Contestar
-
- Correcto. Se está cambiando el orden de los números, lo que demuestra que se está utilizando la ley conmutativa.
- Incorrecto. La ley asociativa implica reagrupar números usando paréntesis, lo que no ocurre en este problema. Más bien, se cambia el orden de los números. La respuesta correcta es el derecho conmutativo.
Uso de las leyes asociativas y conmutativas
Las leyes asociativas y conmutativas son útiles cuando se tiene una expresión con solo adición. Usando la ley conmutativa, los números se pueden reordenar para que los números que son más fáciles de agregar estén uno al lado del otro, y usando la ley asociativa, puedes agruparlos de cualquier manera.
Por ejemplo, estas son algunas de las formas en las que podemos agregar 6+5+4 usando las leyes asociativas y conmutativas. Tenga en cuenta que la respuesta es siempre la misma.
(6+5) +4=11+4=15 (agrupando 6 y 5 para agregar primero)
(5+6) +4=11+4=15 (reordenar 6 y 5)
5+ (6+4) =5+10=15 (agrupando 6 y 4 para agregar primero)
6+ (5+4) =6+9=15 (agrupando 5 y 4 para agregar primero)
6+ (4+5) =6+9=15 (reordenamiento 4 y 5)
(6+4) +5=10+5=15 (agrupando 6 y 4 para agregar primero)
Escribe la expresión 13+28+7 de una manera diferente para que sea más fácil de simplificar. Entonces simplifique.
Solución
|
13+28+7 13+7+28 |
Usando la propiedad conmutativa, reordene los números 7 y 28 ya que 13+7 es más fácil de agregar que 13+28. |
| 20+28 | Usando la propiedad asociativa, agrupa los 13 y 7 juntos y agréguelos primero. |
| 48 | Agregar 20 y 28. |
13+28+7=13+7+28=48
A veces las leyes conmutativas y asociativas pueden hacer que el problema sea lo suficientemente fácil de hacer en tu cabeza.
Jim está comprando 8 peras, 7 manzanas y 2 naranjas. Decidió que el número total de frutos es de 8+7+2. Utilice la propiedad conmutativa para escribir esta expresión de una manera diferente. Entonces encuentra el total.
Solución
|
8+7+2 8+2+7 |
Usando la propiedad conmutativa, reordenar 2 y 7. |
| 10+7 | Usando la propiedad asociativa, agrupa los 8 y 2 y agréguelos primero. |
| 17 | Agrega 10 y 7. |
8+7+2=8+2+7=17
Esto también funciona cuando estás multiplicando más de dos números. Se pueden utilizar libremente las leyes conmutativas y asociativas si la expresión implica sólo multiplicación.
Hay 2 camiones en una cochera, y cada camión tiene capacidad para 60 cajas. Hay 5 computadoras portátiles en cada caja. Encuentra el número de computadoras en la cochera.
Solución
| \(\ 2 \cdot 60 \cdot 5\) | Para encontrar la respuesta, es necesario multiplicar el número de camiones por el número de cajas en cada camión, y, luego por el número de computadoras en cada caja. |
| \(\ 2 \cdot 5 \cdot 60\) | Usando la propiedad conmutativa, reordene el 5 y el 60. Ahora puedes multiplicar\(\ 2 \cdot 5\) primero. |
| \(\ 10 \cdot 60\) | Usando la propiedad asociativa, multiplique el 2 y el 5, 2\ cdot 5=10. |
| 600 | Ahora es más fácil multiplicar 10 y 60 para obtener 600. |
Hay 600 computadoras en la cochera.
Resumen
La propiedad de suma de 0 establece que para cualquier número que se agregue a cero, la suma es el mismo número. La propiedad de multiplicación de 1 establece que para cualquier número multiplicado por uno, esa respuesta es ese mismo número. Cero se llama identidad aditiva, y uno se llama identidad multiplicativa.
Cuando reescribes una expresión por una ley conmutativa, cambias el orden de los números que se van a sumar o multiplicar. Cuando reescribe una expresión usando una ley asociativa, agrupa un par diferente de números usando paréntesis.
Se pueden utilizar las leyes conmutativa y asociativa para reagrupar y reordenar cualquier número en una expresión que implique solo suma. También puedes usar las leyes conmutativa y asociativa para reagrupar y reordenar cualquier número en una expresión que implique solo multiplicación.