1.4.2: La propiedad distributiva

Última actualización
Guardar como PDF

Page ID: 111153

The NROC Project

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

Simplifique el uso de la propiedad distributiva de multiplicación sobre suma.
Simplifique el uso de la propiedad distributiva de multiplicación sobre resta.

Introducción

La propiedad distributiva de la multiplicación es una propiedad muy útil que permite simplificar expresiones en las que se está multiplicando un número por una suma o diferencia. El inmueble establece que el producto de una suma o diferencia, como 6 (5-2), es igual a la suma o diferencia de los productos; en este caso, 6 (5) -6 (2).

Recuerda que hay varias formas de escribir multiplicación. $\ 3 \times 6=3(6)=3 \cdot 6$

$\ 3 \cdot(2+4)=3 \cdot 6=18$

Propiedad distributiva de multiplicación sobre suma

La propiedad distributiva de multiplicación sobre suma se puede utilizar cuando se multiplica un número por una suma. Por ejemplo, supongamos que desea multiplicar 3 por la suma de 10+2.

3 (10+2) =?

Según esta propiedad, se pueden sumar los números y luego multiplicar por 3.

3 (10+2) =3 (12) =36

O bien, primero puedes multiplicar cada adenda por el 3. (Esto se llama distribuir el 3.) Después, puedes agregar los productos.

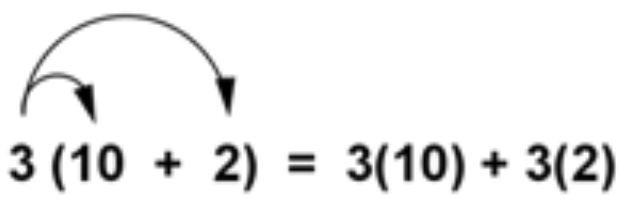
$Screen Shot 2021-04-15 a las 3.49.49 PM.png$

La multiplicación de 3 (10) y 3 (2) se hará cada uno antes de agregar.

3 (10) +3 (2) =30+6=36

Tenga en cuenta que la respuesta es la misma que antes.

Probablemente uses esta propiedad sin saber que la estás usando. Cuando un grupo (digamos 5 de ustedes) pide comida, y ordena lo mismo (digamos que cada uno pide una hamburguesa por $3 cada uno y un refresco por $1 cada uno), puede calcular la factura (sin impuestos) de dos maneras. Puedes averiguar cuánto necesita pagar cada uno de ustedes y multiplicar la suma por el número de ustedes. Entonces, cada uno paga (3+1) y luego multiplicas por 5. Eso es 5 (3+1) =5 (4) =20. O bien, puedes averiguar cuánto costarán las 5 hamburguesas y las 5 sodas y luego encontrar el total. Eso es 5 (3) +5 (1) =15+5=20. De cualquier manera, la respuesta es la misma, $20.

Los dos métodos están representados por las siguientes ecuaciones. En el lado izquierdo, sumamos 10 y 2, y luego multiplicamos por 3. La expresión se reescribe usando la propiedad distributiva del lado derecho, donde distribuimos el 3, luego multiplicamos cada uno por 3 y agregamos los resultados. Observe que el resultado es el mismo en cada caso.

\ (\\ begin {array} {rl}
3 (10+2) &=&3 (10) +3 (2)\\
3 (12) &=&30+6\\
36&=&36
\ end {array}\)

El mismo proceso funciona si el 3 está al otro lado de los paréntesis, como en el siguiente ejemplo.

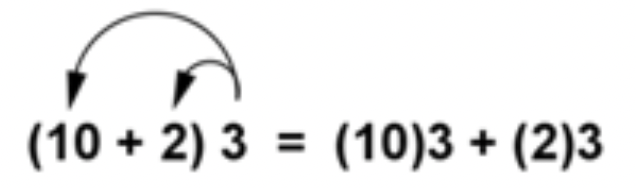
$Screen Shot 2021-04-15 at 3.56.39 PM.png$

Ejemplo

Reescribe la expresión 5 (8+4) usando la propiedad distributiva de multiplicación sobre suma. Entonces simplifica el resultado.

Solución

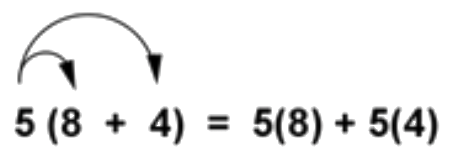$Screen Shot 2021-04-15 en 3.png$	En la expresión original, el 8 y el 4 se agrupan entre paréntesis. Usando flechas, se puede ver cómo se distribuye el 5 a cada adenda. El 8 y el 4 se multiplican cada uno por 5.
40+20=60	Los productos resultantes se suman, resultando en una suma de 60.

5 (8+4) =5 (8) +5 (4) =60

Ejercicio

Reescribe la expresión 30 (2+4) usando la propiedad distributiva de suma.

30 (2+4) +30 (2+4)
30 (2) +30 (4)
30 (6)
30 (24)

Contestar

Incorrecto. Esto estaría duplicando tu valor original. Para distribuir los 30, multiplicar el 2 por 30 y el 4 por 30. La respuesta correcta es 30 (2) +30 (4).
Correcto. El número 30 se distribuye tanto al 2 como al 4, de manera que tanto el 2 como el 4 se multiplican por 30.
Incorrecto. El número 30 no se distribuye en esta respuesta. Para distribuir los 30, multiplicar el 2 por 30 y el 4 por 30. La respuesta correcta es 30 (2) +30 (4).
Incorrecto. Los dígitos 2 y 4 no deben combinarse para formar 24 porque el proceso de adición es incorrecto. El número 30 no se distribuye en esta respuesta. Para distribuir los 30, multiplicar el 2 por 30 y el 4 por 30. La respuesta correcta es 30 (2) +30 (4).

Propiedad distributiva de multiplicación sobre resta

La propiedad distributiva de la multiplicación sobre la resta es como la propiedad distributiva de la multiplicación sobre la suma. Puedes restar los números y luego multiplicar, o puedes multiplicar y luego restar como se muestra a continuación. Esto se llama “distribuir el multiplicador”.

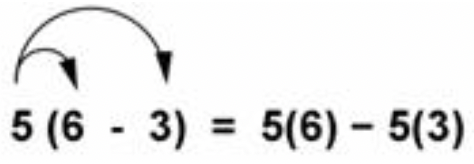
$Screen Shot 2021-04-16 en 1.40.34 PM.png$

El mismo número funciona si el 5 está al otro lado de los paréntesis, como en el siguiente ejemplo.

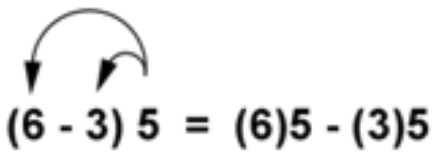
$Screen Shot 2021-04-16 en 1.42.20 PM.png$

En ambos casos, puede entonces simplificar la expresión distribuida para llegar a su respuesta. El siguiente ejemplo, en el que 5 es el multiplicador externo, demuestra que esto es cierto. La expresión de la derecha, que se simplifica usando la propiedad distributiva, se muestra igual a 15, que es el valor resultante a la izquierda también.

\ (\\ begin {array} {rl}
5 (6-3) &=&5 (6) -5 (3)\\
5 (3) &=&30-15\\
15&=&15
\ end {array}\)

Ejemplo

Reescribe la expresión 20 (9-2) usando la propiedad distributiva de multiplicación sobre resta. Entonces simplifique.

Solución

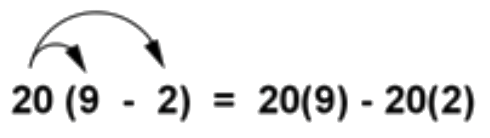$Screen Shot 2021-04-16 en 1.png$	En la expresión original, el 9 y el 2 se agrupan entre paréntesis. Usando flechas, se puede ver cómo se distribuye el 20 a cada número para que el 9 y el 2 se multipliquen ambos por 20 individualmente.
180-40=140	Aquí, el producto resultante de 40 se resta del producto de 180, resultando en una respuesta de 140.

20 (9-2) =20 (9) -20 (2) =140

Ejercicio

Reescribe la expresión 10 (15-6) usando la propiedad distributiva de resta.

10 (6) -10 (15)
10 (9)
10 (6-15)
10 (15) -10 (6)

Contestar

Incorrecto. Aquí, se restaría un número mayor de un número menor, y la respuesta no sería un número entero. La respuesta correcta es 10 (15) -10 (6).
Incorrecto. Los números entre paréntesis se restaron antes de poder distribuir el número 10. La respuesta correcta es 10 (15) -10 (6).
Incorrecto. Probablemente utilizó la ley conmutativa en lugar de la propiedad distributiva. La respuesta correcta es 10 (15) -10 (6).
Correcto. El 10 se distribuye correctamente para que se utilice para multiplicar el 15 y el 6 por separado.

Resumen

Las propiedades distributivas de suma y resta se pueden usar para reescribir expresiones para una variedad de propósitos. Cuando estás multiplicando un número por una suma, puedes sumar y luego multiplicar. También puedes multiplicar primero cada adenda y luego agregar los productos. Esto también se puede hacer con la resta, multiplicando cada número en la diferencia antes de restar. En cada caso, estás distribuyendo el multiplicador externo a cada número entre paréntesis, de manera que se produzca la multiplicación con cada número antes de que ocurra la suma o resta. La propiedad distributiva será útil en futuros cursos de matemáticas, por lo que entenderla ahora te ayudará a construir una base matemática sólida.