1.5.1: Comprensión de exponentes y raíces cuadradas
- Page ID
- 111172
- Evaluar expresiones que contengan exponentes.
- Escribir factores repetidos usando notación exponencial.
- Encuentra una raíz cuadrada de un cuadrado perfecto.
Introducción
Los exponentes proporcionan una forma especial de escribir multiplicación repetida. Los números escritos de esta manera tienen una forma específica, con cada parte proporcionando información importante sobre el número. Escribir números usando exponentes también puede ahorrar mucho espacio. La operación inversa de multiplicación de un número por sí misma se llama encontrar la raíz cuadrada de un número. Esta operación es útil para problemas sobre el área de un cuadrado.
Comprensión de la notación exponencial
La notación exponencial es una forma especial de escribir factores repetidos, por ejemplo\(\ 7 \cdot 7\). La notación exponencial tiene dos partes. Una parte de la notación se llama la base. La base es el número que se está multiplicando por sí mismo. La otra parte de la notación es el exponente, o poder. Este es el pequeño número escrito alto a la derecha de la base. El exponente, o poder, dice cuántas veces usar la base como factor en la multiplicación. En el ejemplo, se\(\ 7 \cdot 7\) puede escribir como\(\ 7^{2}\) (7 es la base y 2 es el exponente). El exponente 2 significa que hay dos factores.
\(\ 7^{2}=7 \cdot 7=49\)
Se puede leer 7 2 como “siete al cuadrado”. Esto se debe a que multiplicar un número por sí mismo se llama “cuadrar un número”. De igual manera, elevar un número a una potencia de 3 se llama “cubing the number”. Se puede leer 7 3 como “siete cubos”.
Se puede leer 2 5 como “dos al quinto poder” o “dos al poder de cinco”, o “dos elevados al poder de cinco”. Lee 8 4 como “ocho al cuarto poder”, o “ocho al poder de cuatro”, u “ocho elevado al poder de cuatro”. Este formato se puede utilizar para leer cualquier número escrito en notación exponencial. De hecho, mientras que 6 3 se lee más comúnmente “seis cubos”, también se puede leer “seis al tercer poder”, o “seis al poder de tres”, o “seis elevado al poder de tres”.
Para encontrar el valor de un número escrito en forma exponencial, reescriba el número como multiplicación repetida y realice la multiplicación. A continuación se muestran dos ejemplos.
Encuentra el valor de 4 2.
Solución
|
4 es la base. 2 es el exponente. |
Un exponente significa multiplicación repetida. La base es 4; 4 es el número que se está multiplicando. El exponente es 2; Esto significa utilizar dos factores de 4 en la multiplicación. |
| \(\ 4^{2}=4 \cdot 4\) | Reescribir como multiplicación repetida. |
| \(\ 4 \cdot 4=16\) | Multiplicar. |
\(\ 4^{2}=16\)
Encuentra el valor de 2 5.
Solución
| \(\ 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2\) |
Reescribe 2 5 como multiplicación repetida. La base es 2, multiplicándose el número. El exponente es 5, el número de veces a utilizar 2 en la multiplicación. |
| \ (\\ begin {array} {r} 2\ cdot 2\ cdot 2\ cdot 2\ cdot 2\ cdot 2\\ 4\ cdot 2\ cdot 2\ cdot 2\ cdot 2\ cdot 2\\ 16\ cdot 2\\ 32 \ end {array}\) |
Realizar multiplicación. |
\(\ 2^{5}=32\)
Encuentra el valor de 4 3.
- 12
- 64
- 256
- 43
- Contestar
-
- Incorrecto. Multiplicar\(\ 4 \cdot 4 \cdot 4\), no\(\ 4 \cdot 3\). La respuesta correcta es 64.
- Correcto. 4\(\ \cdot 4 \cdot 4=64\)
- Incorrecto. Utilizar tres factores de 4 en la multiplicación. La respuesta correcta es 64.
- Incorrecto. 4 3 significa\(\ 4 \cdot 4 \cdot 4\). La respuesta correcta es 64.
Escritura de multiplicación repetida usando exponentes
Escribir multiplicación repetida en notación exponencial puede ahorrar tiempo y espacio. Considera el ejemplo\(\ 5 \cdot 5 \cdot 5 \cdot 5\). Podemos usar notación exponencial para escribir esta multiplicación repetida como 5 4. Ya que 5 se está multiplicando, se escribe como la base. Dado que la base se usa 4 veces en la multiplicación, el exponente es 4. La expresión se\(\ 5 \cdot 5 \cdot 5 \cdot 5\) puede reescribir en notación exponencial taquigráfica como 5 4 y se lee, “cinco al cuarto poder” o “cinco a la potencia de 4”.
Para escribir multiplicación repetida del mismo número en notación exponencial, primero escriba el número que se está multiplicando como base. Después cuente cuántas veces se usa ese número en la multiplicación, y escriba ese número como exponente. Asegúrese de contar los números, no los signos de multiplicación, para determinar el exponente.
Escribir\(\ 7 \cdot 7 \cdot 7\) en notación exponencial.
Solución
| 7 es la base. | La base es el número que se multiplica, 7. |
| Ya que 7 se usa 3 veces, 3 es el exponente. | El exponente dice el número de veces que se multiplica la base. |
\(\ 7 \cdot 7 \cdot 7=7^{3}\)Esto se lee “siete cubos”.
\(\ 10 \cdot 10 \cdot 10 \cdot 10 \cdot 10 \cdot 10\)Escribir. en notación exponencial.
- 1,000,000
- 60
- 10 5
- 10 6
- Contestar
-
- Incorrecto. 1,000,000 es equivalente a\(\ 10 \cdot 10 \cdot 10 \cdot 10 \cdot 10 \cdot 10\), pero no está escrito en notación exponencial. La respuesta correcta es 10 6.
- Incorrecto. Esta respuesta es mucho menor que el valor correcto y no está en notación exponencial. Puede que hayas pensado que seis 10s deberían escribirse\(\ 6 \cdot 10\) y luego simplificarlo a 60. La respuesta correcta es 10 6 porque los seis 10s se multiplican juntos.
Comprensión y computación de raíces cuadradas
Como vio antes, 5 2 se llama “cinco al cuadrado”. “Cinco al cuadrado” significa multiplicar cinco por sí mismo. En matemáticas, llamamos multiplicar un número por sí mismo “cuadrar” el número. Llamamos al resultado de cuadrar un número entero un cuadrado o un cuadrado perfecto. Un cuadrado perfecto es cualquier número que pueda escribirse como un número entero elevado a la potencia de 2. Por ejemplo, 9 es un cuadrado perfecto porque 3 2 es 9. Un número cuadrado perfecto se puede representar como una forma cuadrada, como se muestra a continuación. Vemos que 1, 4, 9, 16, 25 y 36 son ejemplos de cuadrados perfectos.
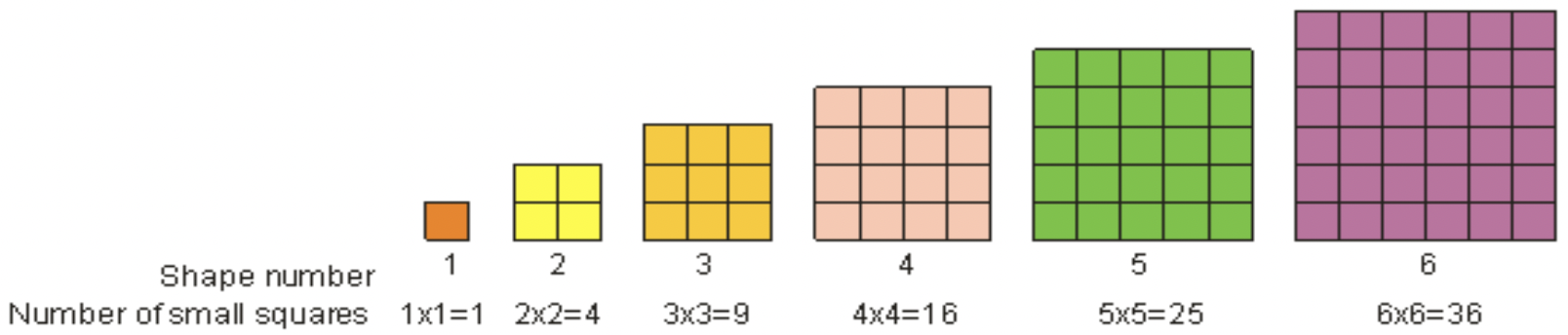
Para cuadrar un número, multiplique el número por sí mismo. 3 al cuadrado\(\ =3^{2}=3 \cdot 3=9\).
A continuación se presentan algunos ejemplos más de cuadrados perfectos.
| 1 cuadrado | 1 2 | \(\ 1 \cdot 1\) | 1 |
| 2 al cuadrado | 2 2 | \(\ 2 \cdot 2\) | 4 |
| 3 al cuadrado | 3 2 | \(\ 3 \cdot 3\) | 9 |
| 4 al cuadrado | 4 2 | \(\ 4 \cdot 4\) | 16 |
| 5 al cuadrado | 5 2 | \(\ 5 \cdot 5\) | 25 |
| 6 al cuadrado | 6 2 | \(\ 6 \cdot 6\) | 36 |
| 7 al cuadrado | 7 2 | \(\ 7 \cdot 7\) | 49 |
| 8 al cuadrado | 8 2 | \(\ 8 \cdot 8\) | 64 |
| 9 al cuadrado | 9 2 | \(\ 9 \cdot 9\) | 81 |
| 10 al cuadrado | 10 2 | \(\ 10 \cdot 10\) | 100 |
La operación inversa de cuadrar un número se llama encontrar la raíz cuadrada de un número. Encontrar una raíz cuadrada es como preguntar, “¿qué número multiplicado por sí mismo me dará este número?” La raíz cuadrada de 25 es 5, porque 5 multiplicado por sí mismo es igual a 25. Las raíces cuadradas se escriben con el símbolo matemático, llamado signo radical, que se ve así:\(\ \sqrt{ }\). Se escribe la “raíz cuadrada de 25"\(\ \sqrt{25}\).
Encuentra\(\ \sqrt{81}\).
Solución
| \(\ \sqrt{81}=9\) |
Piensa, ¿qué número de veces da 81? \(\ 9 \cdot 9=81\) |
\(\ \sqrt{81}=9\)
Encuentra\(\ \sqrt{36}\).
- 6
- 18
- 72
- 7
- Contestar
-
- Correcto. Ya que\(\ 6 \cdot 6=36\),\(\ \sqrt{36}=6\).
- Incorrecto. La raíz cuadrada de 36 es el número que puedes multiplicar por sí mismo para obtener 36. La raíz cuadrada no es el número que multiplicas por 2 para obtener 36. La respuesta correcta es 6, porque\(\ 6 \cdot 6=36\).
- Incorrecto. Es posible que incorrectamente se haya agregado 36 a sí mismo para obtener 72. La raíz cuadrada de 36 es el número que puedes multiplicar por sí mismo para obtener 36. La respuesta correcta es 6, porque\(\ 6 \cdot 6=36\).
- Incorrecto. \(\ 7 \cdot 7=49\), entonces\(\ \sqrt{49}=7\). La respuesta correcta es 6, porque\(\ 6 \cdot 6=36\). Esto significa\(\ \sqrt{36}=6\).
Resumen
La notación exponencial es una forma taquigráfica de escribir multiplicación repetida del mismo número. Un número escrito en notación exponencial tiene una base y un exponente, y cada una de estas partes proporciona información para encontrar el valor de la expresión. La base dice qué número se está multiplicando repetidamente, y el exponente dice cuántas veces se usa la base en la multiplicación. Los exponentes 2 y 3 tienen nombres especiales. Elevar una base a una potencia de 2 se llama “cuadrar” un número. Elevar una base a una potencia de 3 se llama “cubing” un número. La inversa de cuadrar un número es encontrar la raíz cuadrada de un número. Para encontrar la raíz cuadrada de un número, pregúntate: “¿Qué número puedo multiplicar por sí mismo para obtener este número?”


