Saltar al contenido principal
LibreTexts Español

2.1.3: Factores y Primos

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    111432

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de aprendizaje
    • Reconocer (usando la regla de divisibilidad) si un número es divisible por 2, 3, 4, 5, 6, 9 o 10.
    • Encuentra los factores de un número.
    • Determine si un número es primo, compuesto o ninguno.
    • Encuentra la factorización prima de un número.

    Introducción

    Los números naturales, también llamados números de conteo (1, 2, 3, y así sucesivamente), se pueden expresar como un producto de sus factores. Cuando se trabaja con una fracción, a menudo es necesario que la fracción sea lo más simple posible. Esto quiere decir que el numerador y el denominador no tienen otros factores comunes que. Ayudará a encontrar factores, para que posteriormente puedas simplificar y comparar fracciones.

    Pruebas de Divisibilidad

    Cuando un número natural se expresa como producto de otros dos números naturales, esos otros números son factores del número original. Por ejemplo, dos factores de 12 son 3 y 4, porque\(\ 3 \cdot 4=12\).

    Cuando un número se puede dividir por otro número sin resto, decimos que el primer número es divisible por el otro número. Por ejemplo, 20 es divisible por\(\ 4(20 \div 4=5)\). Si un número es divisible por otro número, también es un múltiplo de ese número. Por ejemplo, 20 es divisible por 4, entonces 20 es un múltiplo de 4.

    Las pruebas de divisibilidad son reglas que permiten saber rápidamente si un número es divisible por otro. Hay muchas pruebas de divisibilidad. Estos son algunos de los más útiles y fáciles de recordar:

    • Un número es divisible por 2 si el último (unos) dígito es divisible por 2. Es decir, el último dígito es 0, 2, 4, 6 u 8. (Entonces decimos que el número es un número par.) Por ejemplo, en el número 236, el último dígito es 6. Dado que 6 es divisible por\(\ 2(6 \div 2=3)\), 236 es divisible por 2.
    • Un número es divisible por 3 si la suma de todos los dígitos es divisible por 3. Por ejemplo, la suma de los dígitos de 411 es 4+1+1=6. Dado que 6 es divisible por\(\ 3(6 \div 3=2)\), 411 es divisible por 3.
    • Un número es divisible por 5 si el último dígito es 0 o 5. Por ejemplo, 275 y 1,340 son divisibles por 5 porque los últimos dígitos son 5 y 0.
    • Un número es divisible por 10 si el último dígito es 0. Por ejemplo, 520 es divisible por 10 (el último dígito es 0).
    Otras pruebas de divisibilidad útiles:
    1. : Un número es divisible por 4 si los dos últimos dígitos son divisibles por 4.
    2. : Un número es divisible por 6 si es divisible tanto por 2 como por 3.
    3. : Un número es divisible por 9 si la suma de sus dígitos es divisible por 9

    Aquí hay un resumen de las reglas de divisibilidad más utilizadas.

    Un número es divisible por Ejemplo
    2 si el último dígito es par (0, 2, 4, 6, 8).

    426 sí

    273 no
    3 si la suma de los dígitos es divisible por 3.

    642 sí

    (6+4+2=12, 12 es divisible por 3)

    721 no

    (7+2+1=10, 10 no es divisible por 3)
    4 si los dos últimos dígitos forman un número que es divisible por 4.

    164 sí

    (64 es divisible por 4)

    135 no

    (35 no es divisible por 4)
    5 si el último dígito es 0 o 5.

    685 sí

    432 no
    6 si el número es divisible por 2 y 3.

    324 sí

    (es par y 3+2+4=9)

    411 no

    (aunque divisible por 3, ni siquiera es)
    9 si la suma de los dígitos es divisible por 9.

    279 si

    (2+7+9=18)

    512 no

    (5+1+2=8)
    10 si el último dígito es un 0.

    620 sí.

    238 no

    Si necesitas verificar la divisibilidad de un número sin regla, divide (ya sea usando una calculadora o a mano). Si el resultado es un número sin ninguna parte o resto fraccional, entonces el número es divisible por el divisor. Si olvidas una regla, también puedes usar esta estrategia.

    Ejercicio

    Determina si 522 es divisible por 2, 3, 4, 5, 6, 9 o 10.

    1. 2 y 3 solamente
    2. 4 solamente
    3. 2, 3, 6 y 9 solamente
    4. 4, 5 y 10 solamente
    Responder
    1. Incorrecto. Aunque 522 es divisible por 2 (el último dígito es par) y 3 (5+2+2=9, que es un múltiplo de 3), también es divisible por 6 y 9. La respuesta correcta es 2, 3, 6 y 9 solamente.
    2. Incorrecto. Los dos últimos dígitos (22) no son divisibles por 4, así que 522 no es divisible por 4. 522 tiene un último dígito divisible por 2, así que 522 es divisible por 2. La suma de los dígitos es divisible por 3 (5+2+2=9) y por 9, así que 522 es divisible por 3 y 9. Dado que 522 es divisible por 2 y 3, es divisible por 6. Dado que el último dígito no es 0 o 5, 522 no es divisible por 5 o 10. La respuesta correcta es 2, 3, 6 y 9 solamente.
    3. Correcto. 522 es divisible por 2 (el último dígito es par) y 3 (5+2+2=9, que es un múltiplo de 3). Dado que es divisible por 2 y 3, también es divisible por 6. Además, la suma de los dígitos es divisible por 9, así que 522 es divisible por 9. Dado que el último dígito no es 0 o 5, 522 no es divisible por 5 o 10. El número formado por los dos últimos dígitos, 22, no es divisible por 4, por lo que 522 no es divisible por 4.
    4. Incorrecto. Los dos últimos dígitos no son divisibles por 4, por lo que 522 no es divisible por 4. El último dígito no es 0 o 5 así que 522 no es divisible por 5. El último dígito no es 0, por lo que 522 no es divisible por 10. Sin embargo, 522 es divisible por 2 (el último dígito es par) y 3 (5+2+2=9, que es un múltiplo de 3). Dado que es divisible por 2 y 3, también es divisible por 6. Además, la suma de los dígitos es divisible por 9, así que 522 es divisible por 9. La respuesta correcta es 2, 3, 6 y 9 solamente.

    Números de factorización

    Para encontrar todos los factores de un número, es necesario encontrar todos los números que puedan dividirse en el número original sin un resto. ¡Las reglas de divisibilidad desde arriba serán de suma utilidad!

    Supongamos que necesitas encontrar los factores de 30. Ya que 30 es un número con el que estás familiarizado, y lo suficientemente pequeño, debes conocer muchos de los factores sin aplicar ninguna regla. Puedes comenzar por enumerar los factores a medida que te vienen a la mente:

    \(\ 2 \cdot 15\)

    \(\ 3 \cdot 10\)

    \(\ 5 \cdot 6\)

    ¿Eso es? No del todo. Todos los números naturales excepto 1 también tienen 1 y el número en sí como factores:

    \(\ 1 \cdot 30\)

    Los factores de 30 son 1,2,3,5,6,10,15, y 30.

    Cuando encuentras un factor de un número, puedes encontrar fácilmente otro factor: es el cociente usando ese primer factor como divisor. Por ejemplo, una vez que conoces 2 es un factor de 30, entonces\(\ 30 \div 2\) es otro factor. Un par de factores cuyo producto es un número dado es un par de factores del número original. Entonces, 2 y 15 son un par de factores para 30.

    ¿Qué haces si necesitas factorizar un número mayor y no puedes ver fácilmente sus factores? Ahí es donde las reglas de divisibilidad serán bastante útiles. Aquí hay un conjunto general de pasos que puede seguir:

    1. Comience con y verifique los números secuencialmente, usando reglas de divisibilidad o división.
    2. Cuando encuentres un factor, encuentra el otro número en el par de factores.
    3. Sigue comprobando secuencialmente, hasta llegar al segundo número en el último par de factores que encontraste, o hasta que el resultado de dividir dé un número menor que el divisor.

    Tenga en cuenta que puede dejar de verificar cuando el resultado de dividir sea menor que el número que está verificando. Esto significa que ya has encontrado todos los pares de factores, y continuar con el proceso encontrarías pares que se han encontrado previamente.

    Si un número tiene exactamente dos factores, 1 y él mismo, el número es un número primo. Un número que tiene más factores que él mismo y 1 se llama número compuesto. El número 1 no se considera primo ni compuesto, ya que su único factor es 1. Para determinar si un número es primo, compuesto o ninguno, verifique los factores. Aquí hay algunos ejemplos.

    Número ¿Compuesto, Prime o Ninguno? Explicación
    1 Tampoco 1 no tiene dos factores diferentes, por lo que no es primo.
    2 Prime 2 tiene sólo los factores 2 y 1.
    3 Prime 3 solo tiene los factores 3 y 1.
    4 Composite 4 tiene más de dos factores: 1, 2 y 4, por lo que es compuesto.
    5, 7, 11, 13 Prime Cada número tiene sólo dos factores: 1 y él mismo.
    6, 8, 9, 10, 50, 63 Composite Cada número tiene más de dos factores.
    Ejercicio

    Encuentra todos los factores de 48.

    Responder

    1, 2, 3, 4, 6, 8, 12, 16, 24, 48

    Factorización Prime

    Un número compuesto escrito como un producto de sólo números primos se llama la factorización primo del número. Una forma de encontrar la factorización primo de un número es comenzar con los números primos 2, 3, 5, 7, 11 y así sucesivamente, y determinar si el número es divisible por los primos.

    Por ejemplo, si quieres encontrar la factorización prime de 20, empieza por verificar si 20 es divisible por 2. Sí,\(\ 2 \cdot 10=20\).

    Entonces factor 10, que también es divisible por\(\ 2(2 \cdot 5=10)\).

    Ambos factores son primos, así que puedes parar. La factorización prima de 20 es\(\ 2 \cdot 2 \cdot 5\), la cual se puede escribir usando notación exponencial como\(\ 2^{2} \cdot 5\).

    Una forma de encontrar la factorización prima de un número es usar divisiones sucesivas.

    \ (\\ begin {array} {r}
    10\\\\
    2\ longdiv {2 0}
    \ end {array}\)    		 Divide 20 por 2 para obtener 10. 2 está siendo usado porque es un número primo y un factor de 20. También podrías haber empezado con 5.
    \ (\\ begin {array} {r}
    5\\\\
    2\ longdiv {1 0}\\
    2\ longdiv {2 0}
    \ end {array}\)    		 Después divide 10 por 2 para obtener 5.
    \(\ 2 \cdot 2 \cdot 5\) Multiplicando estos divisores forma la factorización prima de 20.

    Para ayudarle a organizar el proceso de factorización, puede crear un árbol de factores. Este es un diagrama que muestra un par de factores para un número compuesto. Entonces, cada factor que no es primo también se muestra como un par de factores. Puede continuar mostrando pares de factores para factores compuestos, hasta que solo tenga factores primos. Cuando se encuentre un número primo como factor, enciérrelo en un círculo para que pueda encontrarlo más fácilmente después.

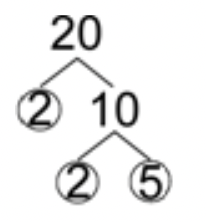
    Screen Shot 2021-04-20 a las 12.58.36 PM.png

    Escrita usando notación exponencial, la factorización prima de 20 vuelve a ser\(\ 2^{2} \cdot 5\).

    Observe que no tiene que comenzar a verificar el número usando la divisibilidad de números primos. Puede factorizar 20 a\(\ 4 \cdot 5\), y luego factor 4 a\(\ 2 \cdot 2\), dando la misma factorización prima:\(\ 2 \cdot 2 \cdot 5\).

    Ahora mira una factorización más complicada.

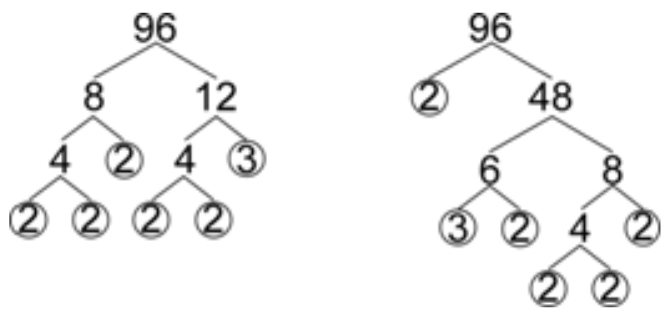
    Screen Shot 2021-04-20 en 1.10.15 PM.png

    Observe que hay dos árboles diferentes, pero ambos producen el mismo resultado: cinco 2s y uno 3. Cada número solo tendrá una factorización prima única. Puede usar cualquier conjunto de pares de factores que desee, siempre y cuando siga factorizando números compuestos.

    Cuando reescribes la factorización prima de\(\ 96(2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 3)\) en notación exponencial, los cinco 2s se pueden escribir como\(\ 2^{5}\). Entonces,\(\ 96=2^{5} \cdot 3\).

    Ejercicio

    Al encontrar la factorización prima de 72, Marie inició un diagrama de árbol utilizando los dos factores 9 y 8. ¿Cuáles de las siguientes afirmaciones son ciertas?

    1. Marie inició el diagrama incorrectamente y debería haber iniciado el diagrama de árbol usando los factores 2 y 36.
    2. El siguiente conjunto de pares de factores de Marie podría ser 3, 3 y 2, 4.
    3. El siguiente conjunto de pares de factores de Marie podría ser 3, 3 y 9, 8.
    4. Marie no tuvo que usar un diagrama de árbol.
    1. 1 solo
    2. 2 solamente
    3. 3 y 4 solamente
    4. 2 y 4 solamente
    Responder
    1. Incorrecto. Marie podría haber comenzado su diagrama de árbol con los factores 2 y 36, pero no tiene que comenzar con esos factores. Empezar con 9 y 8 está bien. La respuesta correcta es D.
    2. Incorrecto. Sí, el siguiente conjunto de pares de factores de Marie podría contener 3, 3 y 2, 4, pero la declaración 4 también es correcta. La respuesta correcta es D.
    3. Incorrecto. El enunciado 4 es correcto: Marie no tiene que usar un diagrama de árbol, pero 3 no es cierto. Al crear una factorización prima, los factores no se combinan con el compuesto anterior. La respuesta correcta es D.
    4. Correcto. El siguiente conjunto de pares de factores de Marie podría leer 3, 3 y 2, 4, ya\(\ 3 \cdot 3\) que es una factorización de 9 y\(\ 2 \cdot 4\) es una factorización de 8. Marie también pudo encontrar la factorización principal usando divisiones sucesivas.

    Resumen

    Encontrar los factores de un número natural significa que encuentras todos los números posibles que se dividirán en el número dado sin un resto. Existen muchas reglas de divisibilidad para ayudarte a encontrar factores más rápidamente. Un número primo es un número que tiene exactamente dos factores. Un número compuesto es un número que tiene más de dos factores. La descomposición primo de un número es el producto de los factores primos del número.

    This page titled 2.1.3: Factores y Primos is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by The NROC Project via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.