2.1.4: Simplificar fracciones
- Page ID
- 111429
- Encuentra una fracción equivalente con un denominador dado.
- Simplifica una fracción en su mínima términos.
Introducción
Las fracciones se utilizan para representar una parte de un todo. Las fracciones que representan la misma parte de un todo se denominan fracciones equivalentes. La factorización, la multiplicación y la división son herramientas útiles para trabajar con fracciones equivalentes.
Fracciones Equivalentes
Usamos fracciones equivalentes todos los días. Cincuenta centavos pueden ser 2 trimestres, y tenemos\(\ \frac{2}{4}\) de un dólar, porque hay 4 trimestres en un dólar. Cincuenta centavos también son 50 centavos de cada 100 centavos, o\(\ \frac{50}{100}\) de un dólar. Ambas fracciones son la misma cantidad de dinero, pero escritas con un numerador y denominador diferentes.
Piensa en una caja de galletas que contenga 3 paquetes de galletas saladas. Dos de estos paquetes son\(\ \frac{2}{3}\) de la caja. Supongamos que cada paquete tiene 30 galletas en él. Dos paquetes también son\(\ 60(30 \cdot 2)\) galletas de\(\ 90(30 \cdot 3)\) galletas saladas. Esto es\(\ \frac{60}{90}\) de la caja. Las fracciones\(\ \frac{2}{3}\) y\(\ \frac{60}{90}\) ambas representan dos paquetes de galletas, por lo que son fracciones equivalentes.
Las fracciones equivalentes representan la misma parte de un todo, aunque el numerador y el denominador sean diferentes. Por ejemplo,\(\ \frac{1}{4}=\frac{5}{20}\). En estos diagramas, ambas fracciones representan una de las cuatro filas del rectángulo.

Ya que\(\ \frac{1}{4}\) y\(\ \frac{5}{20}\) están nombrando la misma parte de un todo, son equivalentes.
Hay muchas maneras de nombrar la misma parte de un todo usando fracciones equivalentes.
Veamos un ejemplo donde necesitas encontrar una fracción equivalente.
John está haciendo galletas para una venta de productos horneados. Hizo 20 galletas grandes, pero quiere regalar solo\(\ \frac{3}{4}\) de ellas para la venta de horneados. ¿Qué fracción de las cookies regala, usando 20 como denominador?
Solución
 |
Empieza con 20 galletas. |
 |
Debido a que el denominador de\(\ \frac{3}{4}\) es 4, hacer 4 grupos de cookies, 5 en cada grupo. |
 |
\(\ \frac{3}{4}=\frac{3 \cdot 5}{4 \cdot 5}\)porque hay 5 cookies en cada grupo. \(\ \frac{3}{4}=\frac{3 \cdot 5}{4 \cdot 5}=\frac{15}{20}\) |
Regala\(\ \frac{15}{20}\) las galletas.
Cuando reagrupas y reconsideras las partes y el todo, estás multiplicando el numerador y el denominador por el mismo número. En el ejemplo anterior, multiplicas 4 por 5 para obtener el denominador necesario de 20, por lo que también necesitas multiplicar el numerador 3 por 5, dando el nuevo numerador de 15.
Para encontrar fracciones equivalentes, multiplique o divida tanto el numerador como el denominador por el mismo número.
Ejemplos:
\(\ \frac{20}{25}=\frac{20 \div 5}{25 \div 5}=\frac{4}{5}\)
\(\ \frac{2}{7}=\frac{2 \cdot 6}{7 \cdot 6}=\frac{12}{42}\)
Escribir una fracción equivalente a\(\ \frac{2}{3}\) que tenga un denominador de 27.
- \(\ \frac{26}{27}\)
- \(\ \frac{11}{27}\)
- \(\ \frac{18}{27}\)
- \(\ \frac{12}{18}\)
- Contestar
-
- Incorrecto. Es posible que haya agregado la diferencia entre los dos denominadores al numerador (27-3=24, 24+2=26). En su lugar, es necesario utilizar un factor multiplicador de\(\ 9(27 \div 3)\). La respuesta correcta es\(\ \frac{18}{27}\).
- Incorrecto. Es posible que haya agregado el factor multiplicador de 9 al numerador. En cambio, multiplique el numerador por este factor. La respuesta correcta es\(\ \frac{18}{27}\).
- Correcto. El factor multiplicador es 9, por lo que el denominador es\(\ 3 \cdot 9=27\) y el numerador es\(\ 2 \cdot 9=18\).
- Incorrecto. Si bien esta es una fracción equivalente a\(\ \frac{2}{3}\), el denominador no es 27. La respuesta correcta es\(\ \frac{18}{27}\).
Simplificación de fracciones
Una fracción está en su forma más simple, o términos más bajos, cuando tiene el menor numerador y el menor denominador posible para nombrar esta parte de un todo. El numerador y denominador no tienen otro factor común que no sea 1.
Aquí hay 10 bloques, 4 de los cuales son de color verde. Entonces, la fracción que es verde es\(\ \frac{4}{10}\). Para simplificar, encuentras un factor común y luego reagrupa los bloques por ese factor.
Simplificar\(\ \frac{4}{10}\).
Solución
 |
Comenzamos con 4 bloques verdes de 10 bloques totales. |
 |
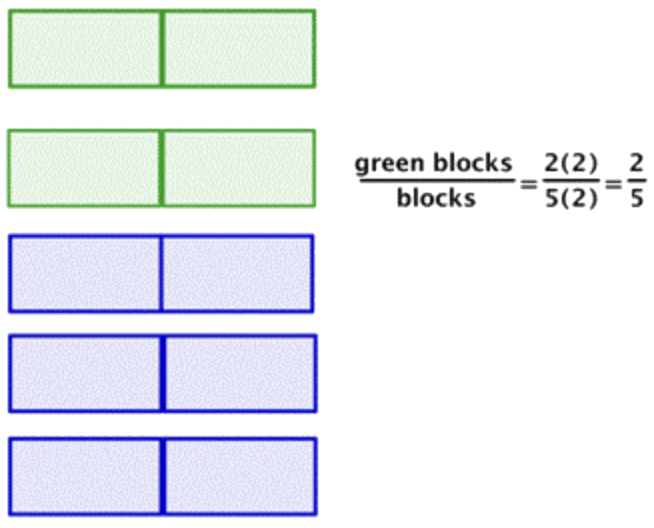
Agrupar los bloques en dos, ya que 2 es un factor común. Tienes 2 grupos de bloques verdes y un total de 5 grupos, cada grupo contiene 2 bloques. |
 |
Ahora, considera los grupos como la parte y tienes 2 grupos verdes de 5 grupos totales. |
\(\ \frac{4}{10}=\frac{2}{5}\)La fracción simplificada es\(\ \frac{2}{5}\).
Una vez que hayas determinado un factor común, puedes dividir los bloques en los grupos dividiendo tanto el numerador como el denominador para determinar el número de grupos que tienes.
Por ejemplo, para simplificar\(\ \frac{6}{9}\) se encuentra un factor común de 3, que dividirá de manera uniforme tanto en 6 como en 9. Entonces, divides 6 y 9 en grupos de 3 para determinar cuántos grupos de 3 contienen. Esto da\(\ \frac{6 \div 3}{9 \div 3}=\frac{2}{3}\), lo que significa 2 de 3 grupos, y\(\ \frac{2}{3}\) es equivalente a\(\ \frac{6}{9}\).
Puede ser necesario agrupar más de una vez. Cada vez, determinar un factor común para el numerador y denominador utilizando las pruebas de divisibilidad, cuando sea posible. Si ambos números son números pares, comience con 2. Por ejemplo:
Simplificar\(\ \frac{32}{48}\).
Solución
| \(\ \frac{32}{48}=\frac{32 \div 2}{48 \div 2}=\frac{16}{24}\) | 32 y 48 tienen un factor común de 2. Dividir cada uno por 2. |
| \(\ \frac{16}{24}=\frac{16 \div 2}{24 \div 2}=\frac{8}{12}\) | 16 y 24 tienen un factor común de 2. Dividir cada uno por 2. |
| \(\ \frac{8}{12}=\frac{8 \div 4}{12 \div 4}=\frac{2}{3}\) | 8 y 12 tienen un factor común de 4. Dividir cada uno por 4. |
| \(\ \frac{32}{48}=\frac{2}{3}\) | \(\ \frac{2}{3}\)es la fracción simplificada equivalente a\(\ \frac{32}{48}\). |
En el ejemplo anterior, 16 es un factor tanto de 32 como de 48, por lo que podría haber acortado la solución.
\(\ \frac{32}{48}=\frac{2 \cdot 16}{3 \cdot 16}=\frac{2}{3}\)
También puedes usar la factorización de primos para ayudar a reagrupar el numerador y el denominador.
Simplificar\(\ \frac{54}{72}\).
Solución
| \(\ \frac{54}{72}=\frac{2 \cdot 3 \cdot 3 \cdot 3}{2 \cdot 2 \cdot 2 \cdot 3 \cdot 3}\) |
La factorización principal de 54 es\(\ 2 \cdot 3 \cdot 3 \cdot 3\). La desfactorización primo de 72 es\(\ 2 \cdot 2 \cdot 2 \cdot 3 \cdot 3\). |
| \(\ \frac{3 \cdot(2 \cdot 3 \cdot 3)}{2 \cdot 2 \cdot(2 \cdot 3 \cdot 3)}\) | Reescribir, encontrando factores comunes. |
| \(\ \frac{3}{2 \cdot 2} \cdot 1\) | \(\ \frac{2 \cdot 3 \cdot 3}{2 \cdot 3 \cdot 3}=1\) |
| \(\ \frac{3}{4}\) | Multiplicar:\(\ 2 \cdot 2\). |
| \(\ \frac{54}{72}=\frac{3}{4}\) | \(\ \frac{3}{4}\)es la fracción simplificada equivalente a\(\ \frac{54}{72}\). |
Observe que al simplificar una fracción, divide el numerador y el denominador por el mismo número, de la misma manera se multiplica por el mismo número para encontrar una fracción equivalente con un denominador mayor. En el ejemplo anterior, podrías haber dividido el numerador y el denominador por 9, un factor común de 54 y 72.
\(\ \frac{54 \div 9}{72 \div 9}=\frac{6}{8}\)
Dado que el numerador (6) y el denominador (8) todavía tienen un factor común, la fracción aún no se encuentra en términos más bajos. Entonces, de nuevo dividir por el factor común 2.
\(\ \frac{6 \div 2}{8 \div 2}=\frac{3}{4}\)
Repita este proceso de dividir por un factor común hasta que el único factor común sea 1.
Para simplificar una fracción en su mínima expresión, divide tanto el numerador como el denominador por sus factores comunes. Repita según sea necesario hasta que el único factor común sea 1.
Simplificar\(\ \frac{36}{72}\).
- \(\ \frac{3}{6}\)
- \(\ \frac{9}{18}\)
- \(\ \frac{18}{38}\)
- \(\ \frac{1}{2}\)
- Contestar
-
- Incorrecto. Si bien\(\ \frac{3}{6}\) es una fracción equivalente a\(\ \frac{36}{72}\), no lo es en términos más bajos. Hay un factor común de 3 en el numerador y denominador. La respuesta correcta es\(\ \frac{1}{2}\).
- Incorrecto. Si bien\(\ \frac{9}{18}\) es una fracción equivalente a\(\ \frac{36}{72}\), no lo es en términos más bajos. Existen otros factores comunes (9 y 3). La respuesta correcta es\(\ \frac{1}{2}\).
- Incorrecto. Es posible que hayas dividido 72 por 2 y obtenido 38 en lugar de 36. \(\ \frac{18}{36}\)es una fracción equivalente a\(\ \frac{36}{72}\), pero no es en términos más bajos. La respuesta correcta es\(\ \frac{1}{2}\).
- Correcto. \(\ \frac{1}{2}\)está en términos más bajos, ya que 1 es el único factor común de 1 y 2.
Resumen
Las fracciones equivalentes no siempre tienen el mismo numerador y denominador, sino que tienen el mismo valor. Una fracción está en términos más bajos cuando el numerador y el denominador de la fracción no comparten otros factores comunes que no sean. Una fracción escrita en términos más bajos se llama fracción simplificada.


