2.1.5: Comparando Fracciones

Objetivos de aprendizaje

• Determinar si dos fracciones son equivalentes.
• Utilice > o < para comparar fracciones.

Introducción

A menudo se necesita saber cuándo una fracción es mayor o menor que otra fracción. Ya que una fracción es parte de un todo, para encontrar la fracción mayor se necesita encontrar la fracción que contiene más del todo. Si las dos fracciones se simplifican a fracciones con un denominador común, entonces puede comparar numeradores. Si los denominadores son diferentes, primero puedes encontrar un denominador común y luego comparar los numeradores.

Determinación de fracciones equivalentes

Dos fracciones son fracciones equivalentes cuando representan la misma parte de un todo. Dado que las fracciones equivalentes no siempre tienen el mismo numerador y denominador, una forma de determinar si dos fracciones son equivalentes es encontrar un denominador común y reescribir cada fracción con ese denominador. Una vez que las dos fracciones tienen el mismo denominador, se puede comprobar para ver si los numeradores son iguales. Si son iguales, entonces las dos fracciones son iguales también.

Una manera de encontrar un denominador común es verificar para ver si un denominador es un factor del otro denominador. Si es así, el denominador mayor puede ser utilizado como denominador común.

Ejemplo

¿Son\(\ \frac{2}{6}\) y fracciones\(\ \frac{8}{18}\) equivalentes?

Solución

Hace\(\ \frac{2}{6}=\frac{8}{18} ?\)	Para resolver este problema, encuentra un denominador común para las dos fracciones. Esto te ayudará a comparar las dos fracciones. Dado que 6 es un factor de 18, se pueden escribir ambas fracciones con 18 como denominador.
\(\ \frac{2 \cdot 3}{6 \cdot 3}=\frac{6}{18}\)	Empezar con la fracción\(\ \frac{2}{6}\). Multiplica el denominador, 6, por 3 para obtener un nuevo denominador de 18. Ya que multiplicas el denominador por 3, también debes multiplicar el numerador por 3.
\(\ \frac{8}{18}\)	La fracción\(\ \frac{8}{18}\) ya tiene un denominador de 18, por lo que puedes dejarla como está.
\(\ \frac{6}{18}\)no es igual\(\ \frac{8}{18}\)	Compara las fracciones. Ahora que ambas fracciones tienen el mismo denominador, 18, puedes comparar numeradores.

\(\ \frac{2}{6}\)y no\(\ \frac{8}{18}\) son fracciones equivalentes.

Cuando un denominador no es un factor del otro denominador, se puede encontrar un denominador común multiplicando los denominadores juntos.

Ejemplo

Determinar si\(\ \frac{3}{6}\) y\(\ \frac{5}{10}\) son fracciones equivalentes.

Solución

\(\ 6 \cdot 10=60\)	Utilizar 60 como denominador común.
\(\ \frac{3}{6}=\frac{3 \cdot 10}{6 \cdot 10}=\frac{30}{60}\)	Multiplica el numerador y denominador de\(\ \frac{3}{6}\) por 10 para obtener 60 en el denominador.
\(\ \frac{5}{10}=\frac{5.6}{10 \cdot 6}=\frac{30}{60}\)	Multiplique el numerador y denominador de\(\ \frac{5}{10}\) por 6.
\(\ \frac{30}{60}=\frac{30}{60}\)	Ahora que los denominadores son iguales, compara los numeradores.
Sí,\(\ \frac{3}{6}\) y\(\ \frac{5}{10}\) son fracciones equivalentes.	Dado que 30 es el valor del numerador para ambas fracciones, las dos fracciones son iguales.

Observe en el ejemplo anterior que puede usar 30 como mínimo denominador común ya que tanto 6 como 10 son factores de 30. Cualquier denominador común funcionará.

En algunos casos, se puede simplificar una o ambas fracciones, lo que puede resultar en un denominador común.

Ejemplo

Determinar si\(\ \frac{2}{3}\) y\(\ \frac{40}{60}\) son fracciones equivalentes.

Solución

\(\ \frac{40}{60}=\frac{40 \div 10}{60 \div 10}=\frac{4}{6}\)	Simplificar\(\ \frac{40}{60}\). Divide el numerador y denominador por el factor común 10.
\(\ \frac{4}{6}=\frac{4 \div 2}{6 \div 2}=\frac{2}{3}\)	\(\ \frac{4}{6}\)todavía no está en términos más bajos, así que vuelve a dividir el numerador y el denominador, esta vez por el factor común 2.
\(\ \frac{2}{3}=\frac{2}{3}\)	Compara las fracciones. Los numeradores y denominadores son los mismos.

Sí,\(\ \frac{2}{3}\) y\(\ \frac{40}{60}\) son fracciones equivalentes.

Nota

En el ejemplo anterior, podrías haber utilizado el factor común de 20 para simplificar\(\ \frac{40}{60}\) directamente a\(\ \frac{2}{3}\).

Determinación de fracciones equivalentes

Para determinar si dos fracciones son equivalentes o no:

Paso 1: Reescribir una o ambas fracciones para que tengan denominadores comunes.

Paso 2: Compara los numeradores para ver si tienen el mismo valor. Si es así, entonces las fracciones son equivalentes.

Ejercicio

¿Cuáles de los siguientes pares de fracciones son equivalentes?

1. \(\ \frac{5}{7}\)y\(\ \frac{7}{5}\)
2. \(\ \frac{12}{30}\)y\(\ \frac{6}{10}\)
3. \(\ \frac{4}{20}\)y\(\ \frac{1}{5}\)
4. \(\ \frac{8}{11}\)y\(\ \frac{8}{22}\)

Contestar

1. Incorrecto. Si bien se utilizan los mismos números, 5 y 7, en cada fracción, los numeradores y denominadores no son iguales, por lo que las fracciones no pueden ser equivalentes. La respuesta correcta es\(\ \frac{4}{20}\) y\(\ \frac{1}{5}\).
2. Incorrecto. 30 es divisible por 10, y 12 es divisible por 6. Sin embargo, no comparten un múltiplo común:\(\ 6 \cdot 2=12\), y\(\ 10 \cdot 3=30\). Esto significa que las fracciones no son equivalentes. La respuesta correcta es\(\ \frac{4}{20}\) y\(\ \frac{1}{5}\).
3. Correcto. Toma la fracción\(\ \frac{1}{5}\) y multiplica tanto el numerador como el denominador por 4. Te quedas con la fracción\(\ \frac{4}{20}\). Esto quiere decir que las dos fracciones son equivalentes.
4. Incorrecto. Los numeradores de las dos fracciones son iguales, pero los denominadores son diferentes. Esto significa que las fracciones no son equivalentes. La respuesta correcta es\(\ \frac{4}{20}\) y\(\ \frac{1}{5}\)

Comparando Fracciones Usando < and >

Cuando se dan dos o más fracciones, muchas veces es útil saber qué fracción es mayor o menor que la otra. Por ejemplo, si el descuento en una tienda está\(\ \frac{1}{3}\) fuera del precio original y el descuento en otra tienda está\(\ \frac{1}{4}\) fuera del precio original, ¿qué tienda está ofreciendo una mejor oferta? Para responder a esta pregunta, y a otras como ésta, se pueden comparar fracciones.

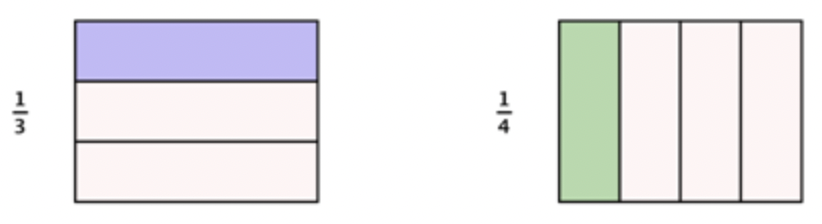
Para determinar qué fracción es mayor, es necesario encontrar un denominador común. A continuación, puede comparar las fracciones directamente. Dado que 3 y 4 son ambos factores de 12, dividirá el conjunto en 12 partes, creará fracciones equivalentes para\(\ \frac{1}{3}\) y\(\ \frac{1}{4}\), y luego comparará.

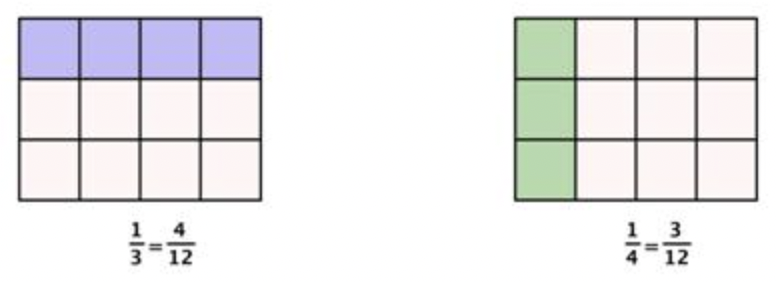
Ahora ves que\(\ \frac{1}{3}\) contiene 4 partes de 12, y\(\ \frac{1}{4}\) contiene 3 partes de 12. Entonces,\(\ \frac{1}{3}\) es mayor que\(\ \frac{1}{4}\).

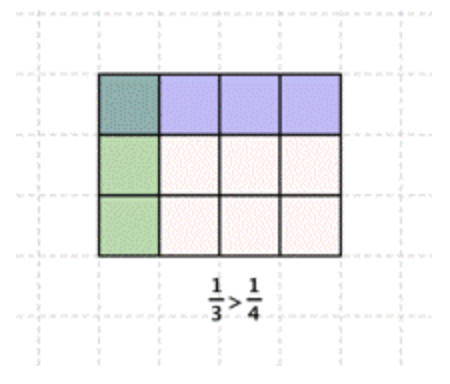
Mientras los denominadores sean los mismos, la fracción con el numerador mayor es la fracción mayor, ya que contiene más partes del conjunto. La fracción con el numerador menor es la fracción menor, ya que contiene menos partes del conjunto.

Recordemos que el símbolo < means “less than”, and the symbol > significa “mayor que”. Estos símbolos son símbolos de desigualdad. Entonces, la declaración verdadera 3<8 se lee como “3 es menor que 8" y la declaración 5>3 se lee como “5 es mayor que 3". Una forma de ayudarte a recordar la distinción entre los dos símbolos es pensar que el extremo más pequeño del símbolo apunta al número menor.

Al igual que con la comparación de números enteros, los símbolos de desigualdad se utilizan para mostrar cuando una fracción es “mayor que” o “menor que” otra fracción.

Comparando Fracciones

Para comparar dos fracciones:

Paso 1: Comparar denominadores. Si son diferentes, reescribe una o ambas fracciones con un denominador común.

Paso 2: Revisa los numeradores. Si los denominadores son los mismos, entonces la fracción con el numerador mayor es la fracción mayor. La fracción con el numerador menor es la fracción menor. Y, como se señaló anteriormente, si los numeradores son iguales, las fracciones son equivalentes.

Ejemplo

< or >Utilízalo para comparar las dos fracciones\(\ \frac{4}{5}\) y\(\ \frac{14}{20}\).

Solución

¿Es\(\ \frac{4}{5}>\frac{14}{20}\) o es\(\ \frac{4}{5}<\frac{14}{20}\)?	No se pueden comparar las fracciones directamente porque tienen diferentes denominadores. Es necesario encontrar un denominador común para las dos fracciones.
\(\ \frac{4}{5}=\frac{?}{20}\)	Dado que 5 es un factor de 20, puedes usar 20 como denominador común.
\(\ \frac{4 \cdot 4}{5 \cdot 4}=\frac{16}{20}\)	Multiplica el numerador y el denominador por 4 para crear una fracción equivalente con un denominador de 20.
\(\ \frac{16}{20}>\frac{14}{20}\)	Compara las dos fracciones. \(\ \frac{16}{20}\)es mayor que\(\ \frac{14}{20}\).
\(\ \frac{4}{5}>\frac{14}{20}\)	Si\(\ \frac{16}{20}>\frac{14}{20}\), entonces\(\ \frac{4}{5}>\frac{14}{20}\), desde\(\ \frac{4}{5}=\frac{16}{20}\).

Ejercicio

¿Cuál de las siguientes es una afirmación verdadera?

1. \(\ \frac{5}{6}<\frac{24}{30}\)
2. \(\ \frac{75}{100}>\frac{9}{12}\)
3. \(\ \frac{4}{16}>\frac{1}{3}\)
4. \(\ \frac{3}{8}<\frac{20}{40}\)

Contestar

1. Incorrecto. \(\ \frac{5}{6}\)es equivalente a\(\ \frac{25}{30}\), y desde 25>24,\(\ \frac{25}{30}>\frac{24}{30}\), lo que significa\(\ \frac{5}{6}>\frac{24}{30}\). La respuesta correcta es\(\ \frac{3}{8}<\frac{20}{40}\).
2. Incorrecto. Ambas fracciones se simplifican a\(\ \frac{3}{4}\), por lo que una no es mayor o menor que la otra. Son equivalentes. La respuesta correcta es\(\ \frac{3}{8}<\frac{20}{40}\).
3. Incorrecto. Encontrar un denominador común, se puede\(\ \frac{12}{48}\) comparar con\(\ \frac{16}{48}\), y ver eso\(\ \frac{12}{48}<\frac{16}{48}\), lo que significa\(\ \frac{4}{16}<\frac{1}{3}\). La respuesta correcta es\(\ \frac{3}{8}<\frac{20}{40}\).
4. Correcto. Simplificando\(\ \frac{20}{40}\), obtienes la fracción equivalente\(\ \frac{1}{2}\). Como todavía no tienes un denominador común, escribe\(\ \frac{1}{2}\) como fracción equivalente con un denominador de 8:\(\ \frac{1}{2}=\frac{1 \cdot 4}{2 \cdot 4}=\frac{4}{8}\). Eso te parece\(\ \frac{3}{8}<\frac{4}{8}\),\(\ \frac{3}{8}<\frac{20}{40}\) así también.

Resumen

Se pueden comparar dos fracciones con denominadores similares comparando sus numeradores. La fracción con el numerador mayor es la fracción mayor, ya que contiene más partes del conjunto. La fracción con el numerador menor es la fracción menor ya que contiene menos partes del conjunto. Si dos fracciones tienen el mismo denominador, entonces los numeradores iguales indican fracciones equivalentes.