2.2.1: Multiplicar fracciones y números mixtos
- Page ID
- 111420
- Multiplica dos o más fracciones.
- Multiplica una fracción por un número entero.
- Multiplica dos o más números mixtos.
- Resolver problemas de aplicación que requieren multiplicación de fracciones o números mixtos.
Introducción
Así como sumas, restas, multiplicas y divides cuando trabajas con números enteros, también usas estas operaciones cuando trabajas con fracciones. Hay muchas ocasiones en las que es necesario multiplicar fracciones y números mixtos. Por ejemplo, esta receta hará 4 trozos de miga:
5 tazas de galletas graham
8 cucharadas de azúcar
\(\ 1 \frac{1}{2}\)tazas de mantequilla derretida
\(\ \frac{1}{4}\)cucharadita de vainilla
Supongamos que solo quieres hacer 2 trozos de miga. Se pueden multiplicar todos los ingredientes por\(\ \frac{1}{2}\), ya que solo se necesita la mitad del número de trozos. Después de aprender a multiplicar una fracción por otra fracción, un número entero o un número mixto, deberías poder calcular los ingredientes necesarios para 2 piecrusts.
Multiplicar fracciones
Cuando multiplicas una fracción por una fracción, estás encontrando una “fracción de una fracción”. Supongamos que tienes\(\ \frac{3}{4}\) de una barra de chocolate y quieres encontrar\(\ \frac{1}{2}\) de la\(\ \frac{3}{4}\):
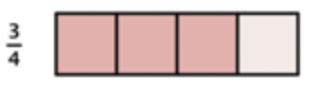
Al dividir cada cuarto por la mitad, se puede dividir la barra de caramelo en octavos.
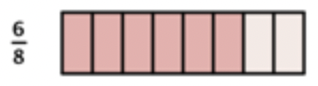
Entonces, elige la mitad de esos para obtener\(\ \frac{3}{8}\).
En ambos casos anteriores, para encontrar la respuesta, se pueden multiplicar los numeradores juntos y los denominadores juntos.
\(\ \frac{a}{b} \cdot \frac{c}{d}=\frac{a \cdot c}{b \cdot d}=\frac{\text { product of the numerators }}{\text { product of the denominators }}\)
Ejemplo:
\(\ \frac{3}{4} \cdot \frac{1}{2}=\frac{3 \cdot 1}{4 \cdot 2}=\frac{3}{8}\)
\(\ \frac{a}{b} \cdot \frac{c}{d} \cdot \frac{e}{f}=\frac{a \cdot c \cdot e}{b \cdot d \cdot f}\)
Ejemplo:
\(\ \frac{1}{3} \cdot \frac{2}{4} \cdot \frac{3}{5}=\frac{1 \cdot 2 \cdot 3}{3 \cdot 4 \cdot 5}=\frac{6}{60}\)
| \(\ \frac{2}{3} \cdot \frac{4}{5}\) | Multiplicar. |
Solución
| \(\ \frac{2 \cdot 4}{3 \cdot 5}\) | Multiplicar los numeradores y multiplicar los denominadores. |
| \(\ \frac{8}{15}\) | Simplificar, si es posible. Esta fracción ya se encuentra en términos más bajos. |
\(\ \frac{8}{15}\)
Si el producto resultante necesita simplificarse a términos más bajos, divida el numerador y el denominador por factores comunes.
| \(\ \frac{2}{3} \cdot \frac{1}{4}\) | Multiplicar. Simplifica la respuesta. |
Solución
| \(\ \frac{2 \cdot 1}{3 \cdot 4}\) | Multiplicar los numeradores y multiplicar los denominadores. |
| \(\ \frac{2}{12}\) | Simplificar, si es posible. |
| \(\ \frac{2 \div 2}{12 \div 2}\) | Simplifica dividiendo el numerador y el denominador por el factor común 2. |
\(\ \frac{2}{3} \cdot \frac{1}{4}=\frac{1}{6}\)
También se puede simplificar el problema antes de multiplicar, dividiendo los factores comunes.
| \(\ \frac{2}{3} \cdot \frac{1}{4}\) | Multiplicar. Simplifica la respuesta. |
Solución
| \(\ \frac{2 \cdot 1}{3 \cdot 4}=\frac{1 \cdot 2}{3 \cdot 4}\) | Reordene los numeradores para que pueda ver una fracción que tenga un factor común. |
| \(\ \frac{1 \cdot 1}{3 \cdot 2}\) |
Simplificar. \(\ \frac{2}{4}=\frac{2 \div 2}{4 \div 2}=\frac{1}{2}\) |
\(\ \frac{2}{3} \cdot \frac{1}{4}=\frac{1}{6}\)
No tienes que usar el atajo “simplificar primero”, pero podría facilitar tu trabajo porque mantiene los números en el numerador y denominador más pequeños mientras trabajas con ellos.
\(\ \frac{3}{4} \cdot \frac{1}{3}\)Multiplicar. Simplifica la respuesta.
- \(\ \frac{3}{12}\)
- \(\ \frac{4}{7}\)
- \(\ \frac{1}{4}\)
- \(\ \frac{36}{144}\)
- Contestar
-
- Incorrecto. \(\ \frac{3}{12}\)es una fracción equivalente a la respuesta correcta\(\ \frac{1}{4}\), pero no es en términos más bajos. Se debe dividir el numerador y el denominador por el factor común 3. La respuesta correcta es\(\ \frac{1}{4}\).
- Incorrecto. Es posible que haya agregado numeradores (3+1) y denominadores añadidos (4+3) en lugar de multiplicar. La respuesta correcta es\(\ \frac{1}{4}\).
- Correcto. Una forma de encontrar esta respuesta es multiplicar numeradores y denominadores,\(\ \frac{3 \cdot 1}{4 \cdot 3}=\frac{3}{12}\), luego simplificar:\(\ \frac{3 \div 3}{12 \div 3}=\frac{1}{4}\).
- Incorrecto. Probablemente encontraste un denominador común, multiplicado correctamente, pero luego olvidaste simplificar. Encontrar un denominador común no es necesario y hace que la multiplicación sea más difícil porque se está trabajando con números mayores de lo necesario. La respuesta correcta es\(\ \frac{1}{4}\).
Multiplicar una Fracción por un Número Entero
Al trabajar tanto con fracciones como con números enteros, es útil escribir el número entero como una fracción impropia (una fracción donde el numerador es mayor o igual que el denominador). Todos los números enteros se pueden escribir con un “1" en el denominador. Por ejemplo:\(\ 2=\frac{2}{1}\),\(\ 5=\frac{5}{1}\), y\(\ 100=\frac{100}{1}\). Recuerda que el denominador dice cuántas partes hay en un todo, y el numerador dice cuántas partes tienes.
\(\ a \cdot \frac{b}{c}=\frac{a}{1} \cdot \frac{b}{c}\)
Ejemplo:
\(\ 4 \cdot \frac{2}{3}=\frac{4}{1} \cdot \frac{2}{3}=\frac{8}{3}\)
A menudo al multiplicar un número entero y una fracción, el producto resultante será una fracción impropia. A menudo es deseable escribir fracciones impropias como un número mixto para la respuesta final. Puede simplificar la fracción antes o después de reescribirla como un número mixto. Vea los ejemplos a continuación.
| \(\ 7 \cdot \frac{3}{5}\) | Multiplicar. Simplifica la respuesta y escribe como un número mixto. |
Solución
| \(\ \frac{7}{1} \cdot \frac{3}{5}\) | Reescribe 7 como la fracción impropia\(\ \frac{7}{1}\). |
| \(\ \frac{7 \cdot 3}{1 \cdot 5}=\frac{21}{5}\) | Multiplicar los numeradores y multiplicar los denominadores. |
| \(\ 4 \frac{1}{5}\) | Reescribir como un número mixto. \(\ 21 \div 5=4\)con un resto de 1. |
\(\ 7 \cdot \frac{3}{5}=4 \frac{1}{5}\)
| \(\ 4 \cdot \frac{3}{4}\) | Multiplicar. Simplifica la respuesta y escribe como un número mixto. |
Solución
| \(\ \frac{4}{1} \cdot \frac{3}{4}\) | Reescribe 4 como la fracción impropia\(\ \frac{4}{1}\). |
| \(\ \frac{4 \cdot 3}{1 \cdot 4}\) | Multiplicar los numeradores y multiplicar los denominadores. |
| \(\ \frac{12}{4}=3\) | Simplificar. |
\(\ 4 \cdot \frac{3}{4}=3\)
\(\ 3 \cdot \frac{5}{6}\)Multiplicar. Simplifica la respuesta y escríbela como un número mixto.
- \(\ 1 \frac{1}{7}\)
- \(\ 2 \frac{1}{2}\)
- \(\ \frac{5}{2}\)
- \(\ \frac{8}{6}\)
- Contestar
-
- Incorrecto. Es posible que hayas agregado los numeradores y agregado los denominadores para obtener\(\ \frac{8}{7}\), que es el número mixto\(\ 1 \frac{1}{7}\). Asegúrate de multiplicar numeradores y multiplicar denominadores. Multiplicar los dos números te da\(\ \frac{15}{6}\), y desde entonces\(\ 15 \div 6=2 \mathrm{R} 3\), el número mixto es\(\ 2 \frac{3}{6}\). La parte fraccionaria simplifica a\(\ \frac{1}{2}\). La respuesta correcta es\(\ 2 \frac{1}{2}\).
- Correcto. Multiplicando los dos números da\(\ \frac{15}{6}\), y ya que\(\ 15 \div 6=2 \mathrm{R} 3\), el número mixto es\(\ 2 \frac{3}{6}\). La parte fraccionaria simplifica a\(\ \frac{1}{2}\).
- Incorrecto. Multiplicar los numeradores y multiplicar los denominadores da como resultado la fracción impropia\(\ \frac{5}{2}\), pero hay que expresarlo como un número mixto. La respuesta correcta es\(\ 2 \frac{1}{2}\).
- Incorrecto. Es posible que hayas agregado numeradores y lo hayas colocado sobre el denominador de 6. Asegúrate de multiplicar numeradores y multiplicar denominadores. Multiplicando los dos números da\(\ \frac{15}{6}\), y ya que\(\ 15 \div 6=2 \mathrm{R} 3\), el número mixto es\(\ 2 \frac{3}{6}\). La parte fraccionaria simplifica a\(\ \frac{1}{2}\). La respuesta correcta es\(\ 2 \frac{1}{2}\).
Multiplicar números mixtos
Si quieres multiplicar dos números mixtos, o una fracción y un número mixto, puedes volver a escribir cualquier número mixto como una fracción impropia.
Entonces, para multiplicar dos números mixtos, reescribir cada uno como una fracción impropia y luego multiplicar como de costumbre. Multiplicar numeradores y multiplicar denominadores y simplificar. Y, como antes, al simplificar, si la respuesta sale como una fracción impropia, entonces convierte la respuesta a un número mixto.
| \(\ 2 \frac{1}{5} \cdot 4 \frac{1}{2}\) | Multiplicar. Simplifica la respuesta y escribe como un número mixto. |
Solución
| \(\ 2 \frac{1}{5}=\frac{11}{5}\) | Cambiar 2\(\ \frac{1}{5}\) a una fracción impropia. \(\ 5 \cdot 2+1=11\), y el denominador es 5. |
| \(\ 4 \frac{1}{2}=\frac{9}{2}\) | Cambiar\(\ 4 \frac{1}{2}\) a una fracción impropia. \(\ 2 \cdot 4+1=9\), y el denominador es 2. |
| \(\ \frac{11}{5} \cdot \frac{9}{2}\) | Reescribir el problema de multiplicación, usando las fracciones incorrectas. |
| \(\ \frac{11 \cdot 9}{5 \cdot 2}=\frac{99}{10}\) | Multiplicar numeradores y multiplicar denominadores. |
| \(\ \frac{99}{10}=9 \frac{9}{10}\) | Escribir como un número mixto. \(\ 99 \div 10=9\)con un resto de 9. |
\(\ 2 \frac{1}{5} \cdot 4 \frac{1}{2}=9 \frac{9}{10}\)
| \(\ \frac{1}{2} \cdot 3 \frac{1}{3}\) | Multiplicar. Simplifica la respuesta y escribe como un número mixto. |
Solución
| \(\ 3 \frac{1}{3}=\frac{10}{3}\) | Cambiar\(\ 3 \frac{1}{3}\) a una fracción impropia. \(\ 3 \cdot 3+1=10\), y el denominador es 3. |
| \(\ \frac{1}{2} \cdot \frac{10}{3}\) | Reescribir el problema de multiplicación, utilizando la fracción impropia en lugar del número mixto. |
| \(\ \frac{1 \cdot 10}{2 \cdot 3}=\frac{10}{6}\) | Multiplicar numeradores y multiplicar denominadores. |
| \(\ \frac{10}{6}=1 \frac{4}{6}\) | Reescribir como un número mixto. \(\ 10 \div 6=1\)con un resto de 4. |
| \(\ 1 \frac{2}{3}\) | Simplifica la parte fraccionaria a términos más bajos dividiendo el numerador y el denominador por el factor común 2. |
\(\ \frac{1}{2} \cdot 3 \frac{1}{3}=1 \frac{2}{3}\)
Como viste antes, a veces es útil buscar factores comunes en el numerador y denominador antes de simplificar los productos.
| \(\ 1 \frac{3}{5} \cdot 2 \frac{1}{4}\) | Multiplicar. Simplifica la respuesta y escribe como un número mixto. |
Solución
| \(\ 1 \frac{3}{5}=\frac{8}{5}\) | Cambiar\(\ 1 \frac{3}{5}\) a una fracción impropia. \(\ 5 \cdot 1+3=8\), y el denominador es 5. |
| \(\ 2 \frac{1}{4}=\frac{9}{4}\) | Cambiar\(\ 2 \frac{1}{4}\) a una fracción impropia. \(\ 4 \cdot 2+1=9\), y el denominador es 4. |
| \(\ \frac{8}{5} \cdot \frac{9}{4}\) | Reescribe el problema de multiplicación usando las fracciones incorrectas. |
| \(\ \frac{8 \cdot 9}{5 \cdot 4}=\frac{9 \cdot 8}{5 \cdot 4}\) | Reordene los numeradores para que pueda ver una fracción que tenga un factor común. |
| \(\ \frac{9 \cdot 8}{5 \cdot 4}=\frac{9 \cdot 2}{5 \cdot 1}\) | Simplificar. \(\ \frac{8}{4}=\frac{8 \div 4}{4 \div 4}=\frac{2}{1}\) |
| \(\ \frac{18}{5}\) | Multiplicar. |
| \(\ \frac{18}{5}=3 \frac{3}{5}\) | Escribir como una fracción mixta. |
\(\ 1 \frac{3}{5} \cdot 2 \frac{1}{4}=3 \frac{3}{5}\)
En el último ejemplo, se encontraría la misma respuesta si multiplicas numeradores y denominadores multiplicados sin eliminar el factor común. Sin embargo, obtendrías\(\ \frac{72}{20}\), y luego necesitarías simplificar más para obtener tu respuesta final.
\(\ 1 \frac{3}{5} \cdot 3 \frac{1}{3}\)
- \(\ \frac{80}{15}\)
- \(\ 5 \frac{5}{15}\)
- \(\ 4 \frac{14}{15}\)
- \(\ 5 \frac{1}{3}\)
- Contestar
-
- Incorrecto. Probablemente escribiste correctamente tanto números mixtos como fracciones impropias. Probablemente también multiplicaste correctamente numeradores y denominadores. Sin embargo, esta fracción impropia aún necesita ser reescrita como un número mixto y simplificada. Dividiendo\(\ 80 \div 15=5\) con un resto de 5 o\(\ 5 \frac{5}{15}\), luego simplificando la parte fraccional, la respuesta correcta es\(\ 5 \frac{1}{3}\).
- Incorrecto. Probablemente escribiste correctamente tanto números mixtos como fracciones impropias. Probablemente también multiplicaste correctamente numeradores y denominadores, y escribiste la respuesta como un número mixto. Sin embargo, el número mixto no está en términos más bajos. \(\ \frac{5}{15}\)se puede simplificar\(\ \frac{1}{3}\) dividiendo el numerador y el denominador por el factor común 5. La respuesta correcta es\(\ 5 \frac{1}{3}\).
- Incorrecto. Este es el resultado de sumar los dos números. Para multiplicar, reescribe cada número mixto como una fracción impropia:\(\ 1 \frac{3}{5}=\frac{8}{5}\) y\(\ 3 \frac{1}{3}=\frac{10}{3}\). A continuación, multiplicar numeradores y multiplicar denominadores:\(\ \frac{8}{5} \cdot \frac{10}{3}=\frac{80}{15}\). Entonces, escribe la fracción impropia resultante como un número mixto:\(\ \frac{80}{15}=5 \frac{5}{15}\). Por último, simplificar la parte fraccionaria dividiendo tanto el numerador como el denominador por el factor común, 5. La respuesta correcta es\(\ 5 \frac{1}{3}\).
- Correcto. Primero, reescribe cada número mixto como una fracción impropia:\(\ 1 \frac{3}{5}=\frac{8}{5}\) y\(\ 3 \frac{1}{3}=\frac{10}{3}\). A continuación, multiplicar numeradores y multiplicar denominadores:\(\ \frac{8}{5} \cdot \frac{10}{3}=\frac{80}{15}\). Después escribe como una fracción mixta\(\ \frac{80}{15}=5 \frac{5}{15}\). Finalmente, simplifique la parte fraccionaria dividiendo tanto el numerador como el denominador por el factor común 5.
Resolver problemas multiplicando fracciones y números mixtos
Ahora que ya sabes cómo multiplicar una fracción por otra fracción, por un número entero, o por un número mixto, puedes usar este conocimiento para resolver problemas que involucran multiplicación y cantidades fraccionarias. Por ejemplo, ahora puedes calcular los ingredientes necesarios para los 2 trozos de miga.
| 5 tazas de galletas graham 8 cucharadas de azúcar\(\ 1 \frac{1}{2}\) tazas de mantequilla derretida\(\ \frac{1}{4}\) cucharadita de vainilla | La receta a la izquierda hace 4 piezas. Encuentra los ingredientes necesarios para hacer solo 2 piezas. |
Solución
| Dado que la receta es para 4 piezas, puedes multiplicar cada uno de los ingredientes por\(\ \frac{1}{2}\) para encontrar las medidas por solo 2 piezas. | |
|
\(\ 5 \cdot \frac{1}{2}=\frac{5}{1} \cdot \frac{1}{2}=\frac{5}{2}\) \(\ 2 \frac{1}{2}\)Se necesitan tazas de galletas Graham. |
5 tazas de galletas graham: Dado que el resultado es una fracción impropia, reescribe\(\ \frac{5}{2}\) como la fracción impropia\(\ 2 \frac{1}{2}\). |
|
\(\ 8 \cdot \frac{1}{2}=\frac{8}{1} \cdot \frac{1}{2}=\frac{8}{2}=4\) Se necesitan 4 cucharadas de azúcar. |
8 cucharadas de azúcar: Este es otro ejemplo de un número entero multiplicado por una fracción. |
|
\(\ \frac{3}{2} \cdot \frac{1}{2}=\frac{3}{4}\) \(\ \frac{3}{4}\)taza de mantequilla derretida es necesaria. |
\(\ 1 \frac{1}{2}\)tazas de mantequilla derretida: Es necesario multiplicar un número mixto por una fracción. Entonces, primero reescribe\(\ 1 \frac{1}{2}\) como la fracción impropia\(\ \frac{3}{2}\):\(\ 2 \cdot 1+1\), y el denominador es 2. Después, reescribe el problema de multiplicación, utilizando la fracción impropia en lugar del número mixto. Multiplicar. |
|
\(\ \frac{1}{4} \cdot \frac{1}{2}=\frac{1}{8}\) \(\ \frac{1}{8}\)se necesita cucharadita de vainilla. |
\(\ \frac{1}{4}\)cucharadita de vainilla: Aquí, multiplicas una fracción por una fracción. |
Los ingredientes necesarios para 2 costras de pastel son:
\(\ 2 \frac{1}{2}\)tazas de galletas graham
4 cucharadas de azúcar
\(\ \frac{3}{4}\)taza de mantequilla derretida
\(\ \frac{1}{8}\)cucharadita de vainilla
A menudo, un problema indica que la multiplicación por una fracción es necesaria mediante el uso de frases como “la mitad de”, “un tercio de” o "\(\ \frac{3}{4}\)de”.
El costo de unas vacaciones es\(\ \$ 4,500\) y usted está obligado a pagar esa\(\ \frac{1}{5}\) cantidad cuando reserve el viaje. ¿Cuánto tendrás que pagar al reservar el viaje?
Solución
| \(\ 4,500 \cdot \frac{1}{5}\) | Necesitas encontrar\(\ \frac{1}{5}\) de 4,500. “De” te dice que te multipliques. |
| \(\ \frac{4,500}{1} \cdot \frac{1}{5}\) | Cambia 4,500 a una fracción impropia reescribiéndola con 1 como denominador. |
| \(\ \frac{4,500}{5}\) | Dividir. |
| \(\ 900\) | Simplificar. |
Tendrá que pagar\(\ \$ 900\) cuando reserve el viaje.
 |
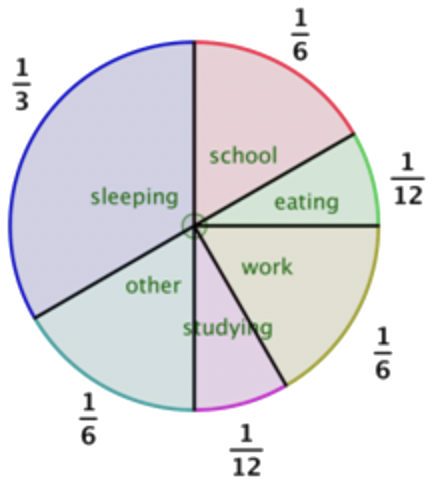El gráfico circular a la izquierda representa la parte fraccionaria de las actividades diarias. Dado un día de 24 horas, ¿cuántas horas se pasan durmiendo? Asistir a la escuela? ¿Comer? Usa el gráfico circular para determinar tus respuestas. |
Solución
| \(\ \frac{1}{3} \cdot 24\)= número de horas durmiendo | Dormir es\(\ \frac{1}{3}\) del pastel, por lo que el número de horas que se pasan durmiendo es\(\ \frac{1}{3}\) de 24. |
| \(\ \frac{1}{3} \cdot \frac{24}{1}=8\) | Reescribe 24 como una fracción impropia con un denominador de 1. |
|
\(\ \frac{24}{3}=8\) 8 horas durmiendo |
Multiplicar numeradores y multiplicar denominadores. Simplificar\(\ \frac{24}{3}\) a 8. |
| \(\ \frac{1}{6} \cdot 24\)= número de horas pasadas en la escuela | Asistir a la escuela es\(\ \frac{1}{6}\) de la tarta, por lo que el número de horas que se dedican a la escuela es\(\ \frac{1}{6}\) de 24. |
| \(\ \frac{1}{6} \cdot \frac{24}{1}\) | Reescribe 24 como una fracción impropia con un denominador de 1. |
|
\(\ \frac{24}{6}=4\) 4 horas asistiendo a la escuela |
Multiplicar numeradores y multiplicar denominadores. Simplificar\(\ \frac{24}{6}\) a 4. |
| \(\ \frac{1}{12} \cdot 24\)= número de horas dedicadas a comer | Comer es\(\ \frac{1}{12}\) del pastel, por lo que el número de horas que se dedican a comer es\(\ \frac{1}{12}\) de 24. |
| \(\ \frac{1}{12} \cdot \frac{24}{1}\) | Reescribe 24 como una fracción impropia con un denominador de 1. |
|
\(\ \frac{24}{12}=2\) 2 horas dedicadas a comer |
Multiplicar numeradores y multiplicar denominadores. Simplificar\(\ \frac{24}{12}\) a 2. |
Horas gastadas:
dormir: 8 horas
asistir a la escuela: 4 horas
comer: 2 horas
Neil compró una docena (12) de huevos. Utilizó\(\ \frac{1}{3}\) de los huevos para el desayuno. ¿Cuántos huevos quedan?
- 8
- 4
- 9
- 3
- Contestar
-
- Correcto. \(\ \frac{1}{3}\)de 12 es\(\ 4\left(\frac{1}{3} \cdot \frac{12}{1}=\frac{12}{3}=4\right)\), por lo que utilizó 4 de los huevos. Porque\(\ 12-4=8\), quedan 8 huevos.
- Incorrecto. \(\ \frac{1}{3}\)de 12 es 4, pero eso da cuántos huevos usó Neil, no cuántos le quedaban. Es necesario restar 4 de 12 para encontrar el número de huevos restantes. La respuesta correcta es 8.
- Incorrecto. Puede que hayas encontrado incorrectamente\(\ \frac{1}{3}\) de 12 ser\(\ \text { 3. } \frac{1}{3}\) de 12 es 4, y luego 12-4 es 8. La respuesta correcta es 8.
- Incorrecto. Necesitas encontrar\(\ \frac{1}{3}\) de 12, que es 4. Después resta 4 de 12 para obtener 8 huevos restantes.
Resumen
Multiplica dos fracciones multiplicando los numeradores y multiplicando los denominadores. A menudo el producto resultante no estará en los términos más bajos, por lo que también debes simplificar. Si una o ambas fracciones son números enteros o números mixtos, primero reescribe cada una como una fracción impropia. Después multiplicar como de costumbre, y simplificar.