2.2.2: Dividir fracciones y números mixtos

Objetivos de aprendizaje

• Encuentra el recíproco de un número.
• Dividir dos fracciones.
• Divide dos números mixtos.
• Dividir fracciones, números mixtos y números enteros.
• Resolver problemas de aplicación que requieran división de fracciones o números mixtos.

Introducción

Hay momentos en los que necesitas usar la división para resolver un problema. Por ejemplo, si pintar una capa de pintura en las paredes de una habitación requiere 3 cuartos de pintura y hay 6 cuartos de pintura, ¿cuántas capas de pintura puedes pintar en las paredes? Divides 6 por 3 para una respuesta de 2 abrigos. También habrá momentos en los que necesites dividir por una fracción. Supongamos que pintar un clóset con una capa solo requirió un\(\ \frac{1}{2}\) cuarto de pintura. ¿Cuántos abrigos se podrían pintar con los 6 cuartos de pintura? Para encontrar la respuesta, es necesario dividir 6 por la fracción,\(\ \frac{1}{2}\).

Reciprocales

Si el producto de dos números es 1, los dos números son recíprocos entre sí. Aquí hay algunos ejemplos:

Número original	recíproco	Producto
\(\ \frac{3}{4}\)	\(\ \frac{4}{3}\)	\(\ \frac{3}{4} \cdot \frac{4}{3}=\frac{3 \cdot 4}{4 \cdot 3}=\frac{12}{12}=1\)
\(\ \frac{1}{2}\)	\(\ \frac{2}{1}\)	\(\ \frac{1}{2} \cdot \frac{2}{1}=\frac{1 \cdot 2}{2 \cdot 1}=\frac{2}{2}=1\)
\(\ 3=\frac{3}{1}\)	\(\ \frac{1}{3}\)	\(\ \frac{3}{1} \cdot \frac{1}{3}=\frac{3 \cdot 1}{1 \cdot 3}=\frac{3}{3}=1\)
\(\ 2 \frac{1}{3}=\frac{7}{3}\)	\(\ \frac{3}{7}\)	\(\ \frac{7}{3} \cdot \frac{3}{7}=\frac{7 \cdot 3}{3 \cdot 7}=\frac{21}{21}=1\)

En cada caso, el número original, cuando se multiplica por su recíproco, equivale a 1.

Para crear dos números que se multipliquen para dar una respuesta de uno, el numerador de uno es el denominador del otro. A veces dices que un número es el “flip” del otro número: flip\(\ \frac{2}{5}\) para obtener el recíproco\(\ \frac{5}{2}\). Para encontrar el recíproco de un número mixto, escríbelo primero como una fracción impropia para que pueda ser “volteado”.

Ejemplo

Encuentra el recíproco de\(\ 5 \frac{1}{4}\).

Solución

\(\ 5 \frac{1}{4}=\frac{21}{4}\)	Reescribir\(\ 5 \frac{1}{4}\) como una fracción impropia. El numerador es\(\ 4 \cdot 5+1=21\).
\(\ \frac{4}{21}\)	Encuentra el recíproco intercambiando (“volteando”) el numerador y el denominador.

Ejercicio

¿De qué es el recíproco\(\ 3 \frac{2}{5}\)?

1. \(\ 3 \frac{5}{2}\)
2. \(\ \frac{17}{5}\)
3. \(\ \frac{5}{17}\)
4. \(\ \frac{5}{2}\)

Contestar

1. Incorrecto. Las partes fraccionarias de esta respuesta y el número mixto original son recíprocas, pero para encontrar el recíproco del número entero, se debe escribir el número mixto como una fracción impropia antes de intercambiar numerador y denominador. La respuesta correcta es\(\ \frac{5}{17}\).
2. Incorrecto. Encontró la fracción incorrecta correcta que representa\(\ 3 \frac{2}{5}\) pero no encontró la recíproca. El recíproco de\(\ \frac{17}{5}\) es\(\ \frac{5}{17}\).
3. Correcto. Primero, escribir\(\ 3 \frac{2}{5}\) como una fracción impropia,\(\ \frac{17}{5}\). El recíproco de\(\ \frac{17}{5}\) se encuentra intercambiando (“volteando”) el numerador y el denominador.
4. Incorrecto. Este es el recíproco correcto para la parte fraccionaria del número mixto, pero con un número mixto, primero hay que escribirlo como una fracción impropia. El número mixto\(\ 3 \frac{2}{5}\) se escribe como la fracción impropia\(\ \frac{17}{5}\). El recíproco de\(\ \frac{17}{5}\) se encuentra intercambiando (“volteando”) el numerador y el denominador.

Dividir una fracción o un número mixto por un número entero

Cuando divides por un número entero, multiplicas por el recíproco del divisor. En el ejemplo de pintura donde necesitas 3 cuartos de pintura para una capa y tienes 6 cuartos de pintura, puedes encontrar el número total de capas que se pueden pintar dividiendo 6 por 3,\(\ 6 \div 3=2\). También se puede multiplicar 6 por el recíproco de 3, que es\(\ \frac{1}{3}\), así se vuelve el problema de multiplicación\(\ \frac{6}{1} \cdot \frac{1}{3}=\frac{6}{3}=2\).

La misma idea funcionará cuando el divisor sea una fracción. Si tienes\(\ \frac{3}{4}\) de una barra de caramelo y necesitas dividirla entre 5 personas, cada persona obtiene\(\ \frac{1}{5}\) de los dulces disponibles:\(\ \frac{1}{5}\) de\(\ \frac{3}{4}\) es\(\ \frac{1}{5} \cdot \frac{3}{4}=\frac{3}{20}\), así que cada persona obtiene\(\ \frac{3}{20}\) de una barra de caramelo entera.

Si tienes una receta que necesita dividirse por la mitad, puedes dividir cada ingrediente por 2, o puedes multiplicar cada ingrediente por\(\ \frac{1}{2}\) para encontrar la nueva cantidad.

De igual manera, con un número mixto, puedes dividir por el número entero o puedes multiplicar por el recíproco. Supongamos que tienes\(\ 1 \frac{1}{2}\) pizzas que quieres dividir equitativamente entre 6 personas.

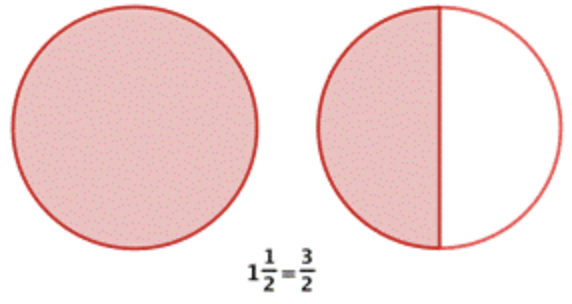
Dividir por 6 es lo mismo que multiplicar por el recíproco de, que es\(\ \frac{1}{6}\). Corta la pizza disponible en seis trozos del mismo tamaño.

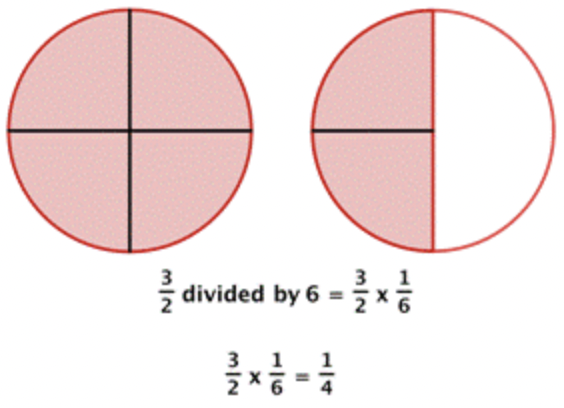
Cada persona obtiene una pieza, así que cada persona obtiene\(\ \frac{1}{4}\) de una pizza.

Dividir una fracción por un número entero es lo mismo que multiplicar por el recíproco, por lo que siempre se puede utilizar la multiplicación de fracciones para resolver tales problemas de división.

Ejemplo

Encuentra\(\ 2 \frac{2}{3} \div 4\). Escribe tu respuesta como un número mixto con cualquier parte de fracción en términos más bajos.

Solución

\(\ 2 \frac{2}{3}=\frac{8}{3}\)	Reescribir\(\ 2 \frac{2}{3}\) como una fracción impropia. El numerador es\(\ 2 \cdot 3+2\). El denominador sigue siendo 3.
\(\ \frac{8}{3} \div 4=\frac{8}{3} \cdot \frac{1}{4}\)	Dividir por 4 o\(\ \frac{4}{1}\) es lo mismo que multiplicar por el recíproco de 4, que es\(\ \frac{1}{4}\).
\(\ \frac{8 \cdot 1}{3 \cdot 4}=\frac{8}{12}\)	Multiplicar numeradores y multiplicar denominadores.
\(\ \frac{2}{3}\)	Simplifica a términos más bajos dividiendo el numerador y el denominador por el factor común 4.

\(\ 2 \frac{2}{3} \div 4=\frac{2}{3}\)

Ejercicio

Encuentra\(\ 4 \frac{3}{5} \div 2\) Simplifica la respuesta y escribe como un número mixto.

1. \(\ 2 \frac{3}{10}\)
2. \(\ \frac{10}{23}\)
3. \(\ \frac{23}{10}\)
4. \(\ 9 \frac{1}{5}\)

Contestar

1. Correcto. Escribir\(\ 4 \frac{3}{5}\) como la fracción impropia\(\ \frac{23}{5}\). Entonces multiplicar por\(\ \frac{1}{2}\), el recíproco de 2. Esto da la fracción impropia\(\ \frac{23}{10}\), y el número mixto es\(\ 23 \div 10=2 \mathrm{R} 3\), que es\(\ 2 \frac{3}{10}\).
2. Incorrecto. Después de cambiar el número mixto a una fracción impropia, es posible que haya invertido\(\ \frac{23}{5}\) en lugar de 2. Mantener\(\ \frac{23}{5}\), y multiplicar por el recíproco de 2, dándote\(\ \frac{23}{5} \cdot \frac{1}{2}=\frac{23}{10}\). Por último, escribe\(\ \frac{23}{10}\) como un número mixto,\(\ 23 \div 10=2 \mathrm{R} 3\), que es\(\ 2 \frac{3}{10}\).
3. Incorrecto. Esta es la fracción incorrecta correcta, pero aún necesita escribir la respuesta final como un número mixto,\(\ 23 \div 10=2 \mathrm{R} 3\), que es\(\ 2 \frac{3}{10}\).
4. Incorrecto. Quizás te hayas olvidado de encontrar el recíproco de 2 antes de multiplicar. Una vez que tengas la fracción impropia para\(\ 4 \frac{3}{5}\), que es\(\ \frac{23}{5}\), multiplica por el recíproco de 2, que es\(\ \frac{1}{2}\), dándote\(\ \frac{23}{5} \cdot \frac{1}{2}=\frac{23}{10}\). Por último, escribe\(\ \frac{23}{10}\) como un número mixto,\(\ 23 \div 10=2 \mathrm{R} 3\), que es\(\ 2 \frac{3}{10}\).

Dividiendo por una Fracción

En ocasiones se necesita resolver un problema que requiere dividir por una fracción. Supongamos que tienes una pizza que ya está cortada en 4 rebanadas. ¿Cuántas\(\ \frac{1}{2}\) rebanadas hay?

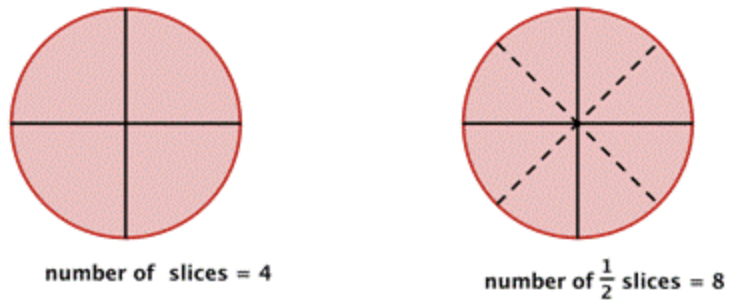
Hay 8 rebanadas. Se puede ver que dividir 4 por\(\ \frac{1}{2}\) da el mismo resultado que multiplicar 4 por 2. ¿Qué pasaría si necesitabas dividir cada rebanada en tercios?

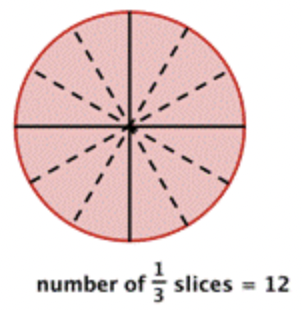
Tendrías 12 rebanadas, lo que es lo mismo que multiplicar 4 por 3.

Dividir con fracciones

Paso 1: Encuentra el recíproco del número que sigue al símbolo de división.

Paso 2: Multiplica el primer número (el anterior al símbolo de división) por el recíproco del segundo número (el que está después del símbolo de división).

Ejemplos:

\(\ 6 \div \frac{2}{3}=6 \cdot \frac{3}{2} \text { and } \frac{2}{5} \div \frac{1}{3}=\frac{2}{5} \cdot \frac{3}{1}\)

Una manera fácil de recordar cómo dividir fracciones es la frase “mantener, cambiar, voltear”. Esto significa MANTENER el primer número, CAMBIAR el signo de división a multiplicación, y luego FLIP (use el recíproco) del segundo número.

Ejemplo

\(\ \frac{2}{3} \div \frac{1}{6}\)

Dividir.

Solución

\(\ \frac{2}{3} \cdot \frac{6}{1}\)	Multiplicar por el recíproco: Mantener\(\ \frac{2}{3}\)\(\ \cdot\),\(\ \div\) cambiar y voltear\(\ \frac{1}{6}\).
\(\ \frac{2 \cdot 6}{3 \cdot 1}=\frac{12}{3}\)	Multiplicar numeradores y multiplicar denominadores.
\(\ \frac{12}{3}=4\)	Simplificar.

\(\ \frac{2}{3} \div \frac{1}{6}=4\)

Ejemplo

\(\ \frac{3}{5} \div \frac{2}{3}\)

Dividir.

Solución

\(\ \frac{3}{5} \cdot \frac{3}{2}\)	Multiplicar por el recíproco: Mantener\(\ \frac{3}{5}\)\(\ \cdot\),\(\ \div\) cambiar y voltear\(\ \frac{2}{3}\).
\(\ \frac{3 \cdot 3}{5 \cdot 2}=\frac{9}{10}\)	Multiplicar numeradores y multiplicar denominadores.

\(\ \frac{3}{5} \div \frac{2}{3}=\frac{9}{10}\)

Al resolver un problema de división multiplicando por lo recíproco, recuerde escribir todos los números enteros y números mixtos como fracciones impropias. La respuesta final debe simplificarse y escribirse como un número mixto.

Ejemplo

\(\ 2 \frac{1}{4} \div \frac{3}{4}\)

Dividir.

Solución

\(\ \frac{9}{4} \cdot \frac{4}{3}\)	Escribe 2\(\ \frac{1}{4}\) como una fracción impropia.
\(\ \frac{9}{4} \cdot \frac{4}{3}\)	Multiplicar por el recíproco: Mantener\(\ \frac{9}{4}\)\(\ \cdot\),\(\ \div\) cambiar y voltear\(\ \frac{3}{4}\).
\(\ \frac{9 \cdot 4}{4 \cdot 3}=\frac{36}{12}\)	Multiplicar numeradores y multiplicar denominadores.
\(\ \frac{36}{12}=3\)	Simplificar.

\(\ 2 \frac{1}{4} \div \frac{3}{4}=3\)

Ejemplo

\(\ 3 \frac{1}{5} \div 2 \frac{1}{10}\)

Dividir. Simplifica la respuesta y escribe como un número mixto.

Solución

\(\ \frac{16}{5} \div \frac{21}{10}\)	Escribir\(\ 3 \frac{1}{5}\) y\(\ 2 \frac{1}{10}\) como fracciones impropias.
\(\ \frac{16}{5} \cdot \frac{10}{21}\)	Multiplicar por el recíproco de\(\ \frac{21}{10}\).
\(\ \frac{16 \cdot 10}{5 \cdot 21}\)	Multiplicar numeradores, multiplicar denominadores.
\(\ \frac{16 \cdot 10}{21 \cdot 5}\)	Reagruparse.
\(\ \frac{16 \cdot 2}{21 \cdot 1}\)	Simplificar:\(\ \frac{10}{5}=\frac{2}{1}\)
\(\ \frac{16 \cdot 2}{21 \cdot 1}=\frac{32}{21}\)	Multiplicar.
\(\ \frac{32}{21}=1 \frac{11}{21}\) \(\ 3 \frac{1}{5} \div 2 \frac{1}{10}=1 \frac{11}{21}\)	Reescribir como un número mixto.

\(\ 3 \frac{1}{5} \div 2 \frac{1}{10}=1 \frac{11}{21}\)

Ejercicio

Encuentra\(\ 5 \frac{1}{3} \div \frac{2}{3}\). Simplifica la respuesta y escribe como un número mixto.

1. \(\ 4 \frac{1}{2}\)
2. \(\ 3 \frac{5}{9}\)
3. \(\ \frac{16}{2}\)
4. \(\ 8\)

Contestar

1. Incorrecto. Es posible que hayas escrito incorrectamente\(\ 5 \frac{1}{3}\) como la fracción impropia\(\ \frac{9}{3}\). Para escribir\(\ 5 \frac{1}{3}\) como una fracción impropia, multiplicar 5 por 3 y sumar 1. El denominador es 3. \(\ 5 \frac{1}{3}=\frac{16}{3}\). Entonces cambia la división a multiplicación y multiplica por el recíproco de\(\ \frac{2}{3}\), que es\(\ \frac{3}{2}\), dándote\(\ \frac{16}{3} \cdot \frac{3}{2}=\frac{3}{3} \cdot \frac{16}{2}=\frac{16}{2}=8\).
2. Incorrecto. Quizás te hayas olvidado de usar el recíproco de\(\ \frac{2}{3}\). Después de encontrar la fracción impropia\(\ \frac{16}{3}\) que representa\(\ 5 \frac{1}{3}\), cambia la división a la multiplicación y usa el recíproco de\(\ \frac{2}{3}\), dándote\(\ \frac{16}{3} \cdot \frac{3}{2}=\frac{3}{3} \cdot \frac{16}{2}=\frac{16}{2}=8\).
3. Incorrecto. Esta es la fracción incorrecta correcta, pero la respuesta final tiene que ser un número mixto. Divide 16 por 2, que es 8 y ningún resto. No hay parte fraccionaria, por lo que la respuesta es un número entero, 8.
4. Correcto. Escribir 5\(\ \frac{1}{3}\) como una fracción impropia,\(\ \frac{16}{3}\). Entonces multiplicar por el recíproco de\(\ \frac{2}{3}\), que es\(\ \frac{3}{2}\), dándote\(\ \frac{16}{3} \cdot \frac{3}{2}=\frac{3}{3} \cdot \frac{16}{2}=\frac{16}{2}=8\).

Dividir fracciones o números mixtos para resolver problemas

El uso de la multiplicación por el recíproco en lugar de la división puede ser muy útil para resolver problemas que requieren división y fracciones.

Ejemplo

Un cocinero tiene\(\ 18 \frac{3}{4}\) libras de carne molida. ¿Cuántas hamburguesas de un cuarto de libra puede hacer?

Solución

\(\ 18 \frac{3}{4} \div \frac{1}{4}\)	Necesitas encontrar cuántos cuartos de libras hay\(\ 18 \frac{3}{4}\), en así usa división.
\(\ \frac{75}{4} \div \frac{1}{4}\)	Escribir\(\ 18 \frac{3}{4}\) como una fracción impropia.
\(\ \frac{75}{4} \cdot \frac{4}{1}\)	Multiplicar por el recíproco.
\(\ \frac{75 \cdot 4}{4 \cdot 1}\)	Multiplicar numeradores y multiplicar denominadores.
\(\ \frac{4}{4} \cdot \frac{75}{1}\)	Reagruparse y simplificar\(\ \frac{4}{4}\), que es 1.

75 hamburguesas

Ejemplo

Un niño necesita tomar\(\ 2 \frac{1}{2}\) cucharadas de medicamento al día en 4 dosis iguales. ¿Cuánto medicamento hay en cada dosis?

Solución

\(\ 2 \frac{1}{2} \div 4\)	Necesitas hacer 4 dosis iguales, para que puedas usar la división.
\(\ \frac{5}{2} \div 4\)	Escribir\(\ 2 \frac{1}{2}\) como una fracción impropia.
\(\ \frac{5}{2} \cdot \frac{1}{4}\)	Multiplicar por el recíproco.
\(\ \frac{5 \cdot 1}{2 \cdot 4}=\frac{5}{8}\)	Multiplicar numeradores y multiplicar denominadores. Simplificar, si es posible.

\(\ \frac{5}{8}\)cucharada en cada dosis.

Ejercicio

\(\ \frac{2}{5}\)¿Cuántos saleros de taza se pueden llenar de tazas de sal?

1. \(\ 4 \frac{4}{5}\)
2. \(\ \frac{60}{2}\)
3. \(\ 30\)
4. \(\ \frac{1}{30}\)

Contestar

1. Incorrecto. Probablemente olvidaste encontrar el recíproco de\(\ \frac{2}{5}\). Encuentra\(\ 12 \div \frac{2}{5}\). Mantener el 12, cambiar división a multiplicación, y utilizar el recíproco (“flip”) de\(\ \frac{2}{5}\), dándole:\(\ 12 \cdot \frac{5}{2}=\frac{12}{1} \cdot \frac{5}{2}=\frac{60}{2}=30\).
2. Incorrecto. Aún necesitas encontrar el número mixto que representa\(\ \frac{60}{2}\). En este caso, 60 dividido por 2 es\(\ 30 \mathrm{R} 0\), por lo que la respuesta es un número entero, 30.
3. Correcto. \(\ 12 \div \frac{2}{5}\)mostrará cuántos saleros se pueden llenar. Escribe 12 como\(\ \frac{12}{1}\) y multiplica por el recíproco (“flip”) de\(\ \frac{2}{5}\), dándote\(\ \frac{12}{1} \cdot \frac{5}{2}=\frac{60}{2}=30\).
4. Incorrecto. Usaste incorrectamente la expresión\(\ \frac{2}{5} \div 12\). Esto mostrará cuántos grupos de 12 hay en\(\ \frac{2}{5}\). Es necesario encontrar cuántos grupos de\(\ \frac{2}{5}\) hay en 12, que es\(\ 12 \div \frac{2}{5}\). Entonces escribe 12 como\(\ \frac{12}{1}\) y multiplica por el recíproco (“flip”) de\(\ \frac{2}{5}\), dándote\(\ 12 \cdot \frac{5}{2}=\frac{12}{1} \cdot \frac{5}{2}=\frac{60}{2}=30\).

Resumen

La división es lo mismo que multiplicar por lo recíproco. Al trabajar con fracciones, esta es la forma más fácil de dividir. Ya sea que dividas por un número o multipliques por el recíproco del número, el resultado será el mismo. Puedes usar estas técnicas para ayudarte a resolver problemas que involucren división, fracciones y/o números mixtos.