2.3.1: Sumando fracciones y números mixtos
- Page ID
- 111418
- Agrega fracciones con denominadores similares.
- Encuentra el múltiplo mínimo común (MCM) de dos o más números.
- Encuentra el denominador común de fracciones con denominadores diferentes.
- Sumar fracciones con denominadores distintos.
- Sumar números mixtos con denominadores similares y diferentes.
- Resolver problemas de aplicación que requieran la adición de fracciones o números mixtos.
Introducción
Las fracciones se utilizan en muchas áreas de la vida cotidiana: recetas, carpintería, lluvia, registros de tiempo y medidas, por nombrar solo algunos. A veces tienes partes de enteros que necesitas combinar. Así como puedes sumar números enteros, puedes sumar fracciones y números mixtos. Considera, por ejemplo, cómo determinar la precipitación mensual si conoces las precipitaciones diarias en pulgadas. Hay que sumar fracciones. También, considere a varios pintores que están trabajando para pintar una casa junto con múltiples latas de pintura. Podrían sumar las fracciones de lo que queda en cada lata para determinar si hay suficiente pintura para terminar el trabajo o si necesitan comprar más.
Sumando fracciones con denominadores similares
Cuando las piezas son del mismo tamaño, se pueden agregar fácilmente. Considera las imágenes a continuación mostrando las fracciones\(\ \frac{3}{6}\) y\(\ \frac{2}{6}\).
Esta imagen representa\(\ \frac{3}{6}\) sombreada porque 3 de cada 6 bloques están sombreados.

Esta imagen representa\(\ \frac{2}{6}\) sombreada porque 2 de cada 6 bloques están sombreados.

Si agrega estos bloques sombreados juntos, está agregando\(\ \frac{3}{6}+\frac{2}{6}\).
Puede crear una nueva imagen que muestre 5 bloques sombreados en un rectángulo que contiene 6 bloques.
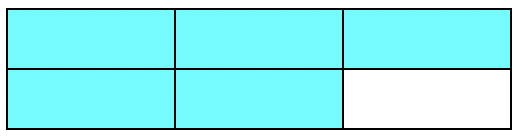
Entonces,\(\ \frac{3}{6}+\frac{2}{6}=\frac{5}{6}\).
Sin dibujar rectángulos y cajas de sombreado, puedes obtener esta respuesta simplemente agregando los numeradores, 3+2, y manteniendo el denominador, 6, igual. Este procedimiento funciona para sumar cualesquiera fracciones que tengan el mismo denominador, llamadas denominadores similares.
| \(\ \frac{3}{5}+\frac{1}{5}\) | Agregar. |
Solución
| \(\ \frac{3+1}{5}\) | Dado que el denominador de cada fracción es 5, estas fracciones tienen denominadores similares. |
| \(\ \frac{4}{5}\) | Entonces, sumar los numeradores y escribir la suma sobre el denominador, 5. |
\(\ \frac{3}{5}+\frac{1}{5}=\frac{4}{5}\)
| \(\ \frac{3}{8}+\frac{5}{8}\) | Agregar. Simplifica la respuesta. |
Solución
| \(\ \frac{3}{8}+\frac{5}{8}=\frac{3+5}{8}=\frac{8}{8}\) | Los denominadores son iguales, así que sumamos los numeradores. |
| \(\ \frac{8}{8}=1\) | Simplifica la fracción. |
\(\ \frac{3}{8}+\frac{5}{8}=1\)
| \(\ \frac{11}{12}+\frac{5}{12}\) | Agregar. Simplifica la respuesta y escribe como un número mixto. |
Solución
| \(\ \frac{11}{12}+\frac{5}{12}=\frac{11+5}{12}=\frac{16}{12}\) | Los denominadores son iguales, así que sumamos los numeradores. |
| \(\ \frac{16}{12}=\frac{16 \div 4}{12 \div 4}=\frac{4}{3}\) | Simplifica la fracción. 16 y 12 tienen un factor común de 4. |
| \(\ \frac{4}{3}=1 \frac{1}{3}\) | Escribe la fracción impropia como un número mixto, dividiendo:\(\ 4 \div 3=1\) con un resto de 1. |
\(\ \frac{11}{12}+\frac{5}{12}=1 \frac{1}{3}\)
En el ejemplo anterior, la fracción se simplificó y luego se convirtió a un número mixto. Con la misma facilidad podría haber convertido primero la fracción impropia a un número mixto y luego simplificar la fracción en el número mixto. Observe que se alcanza la misma respuesta con ambos métodos.
\(\ \frac{16}{12}=1 \frac{4}{12}\)
La fracción\(\ \frac{4}{12}\) se puede simplificar. \(\ \frac{4}{12}=\frac{4 \div 4}{12 \div 4}=\frac{1}{3}\)
Pero, ¡no te olvides del 1 que forma parte del número mixto! La respuesta final es\(\ 1 \frac{1}{3}\).
- Sumar los numeradores (el número en la parte superior de cada fracción).
- Mantenga el denominador (el número inferior) igual.
- Simplificar a los términos más bajos.
\(\ \frac{7}{10}+\frac{8}{10}\)Agregar. Simplifica la respuesta y escribe como un número mixto.
- \(\ \frac{15}{20}\)
- \(\ \frac{9}{10}\)
- \(\ \frac{3}{2}\)
- \(\ 1 \frac{1}{2}\)
- Contestar
-
- Incorrecto. Cuando agrega fracciones con denominadores similares, solo agrega los numeradores, no los denominadores. Mantener el denominador igual. La respuesta correcta es\(\ 1 \frac{1}{2}\).
- Incorrecto. Para sumar dos fracciones con el mismo denominador, sumar los dos numeradores juntos. Entonces simplifica la fracción. La respuesta correcta es\(\ 1 \frac{1}{2}\).
- Incorrecto. La respuesta debe expresarse como un número mixto simplificado, no como una fracción impropia. La respuesta correcta es\(\ 1 \frac{1}{2}\).
- Correcto. \(\ \frac{7+8}{10}=\frac{15}{10}=1 \frac{5}{10}=1 \frac{1}{2}\).
Encontrar múltiplos menos comunes
A veces las fracciones no tienen el mismo denominador. Tienen denominadores distintos. Piensa en el ejemplo de los pintores de casas. Si un pintor tiene\(\ \frac{2}{3}\) lata de pintura y su compañero de pintura tiene\(\ \frac{1}{2}\) lata de pintura, ¿cuánto tienen en total? ¿Cómo se pueden sumar estas fracciones cuando no tienen denominadores similares?
La respuesta es que puedes reescribir una o ambas fracciones para que tengan el mismo denominador. A esto se le llama encontrar un denominador común. Si bien cualquier denominador común servirá, es útil encontrar el múltiplo menos común de los dos números en el denominador porque esto ahorrará tener que simplificar al final. El múltiplo menos común es el menor número que es un múltiplo de dos o más números. El múltiplo menos común a veces se abrevía LCM.
Hay varias formas de encontrar múltiplos comunes, algunos de los cuales usaste al comparar fracciones. Para encontrar el múltiplo menos común (LCM), puede enumerar los múltiplos de cada número y determinar qué múltiplos tienen en común. El menor de estos números será el múltiplo menos común. Considera los números 4 y 6. A continuación se muestran algunos de sus múltiplos. Se puede ver que tienen varios múltiplos comunes, y el menor de estos es 12.
| 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 | 52 | 56 | 60 | 64 |
| 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 68 |
Encuentra el múltiplo menos común de 30 y 50.
Solución
| 30, 60, 90, 120, 150, 180, 210, 240 | Enumere algunos múltiplos de 30. |
| 50, 100, 150, 200, 250 | Enumere algunos múltiplos de 50. |
| 150 se encuentra en ambas listas de múltiplos. | Busca el menor número que se encuentra en ambas listas. |
El múltiplo menos común de 30 y 50 es 150.
El otro método para encontrar el múltiplo menos común es usar la factorización prima. Este es el método que necesitas para trabajar con expresiones racionales. A continuación se muestra cómo funciona el método factor con el ejemplo numérico, 4 y 6.
Comience por encontrar la factorización prima de cada denominador:
\(\ 4=2 \cdot 2\)
\(\ 6=3 \cdot 2\)
Identificar el mayor número de veces que aparece cualquier factor en cualquiera de las factorizaciones y multiplica esos factores para obtener el múltiplo menos común. Para 4 y 6, sería:
\(\ 3 \cdot 2 \cdot 2=12\)
Observe que 2 se incluye dos veces, porque aparece dos veces en la factorización prima de 4. 12 es el múltiplo menos común de 4 y 6.
El siguiente ejemplo también muestra cómo usar la factorización prima.
Encuentra el mínimo común múltiplo de 28 y 40.
Solución
| \(\ 28=2 \cdot 2 \cdot 7\) | Escribe la factorización prime de 28. |
| \(\ 40=2 \cdot 2 \cdot 2 \cdot 5\) | Escribe la factorización prime de 40. |
| \(\ 2 \cdot 2 \cdot 2 \cdot 5 \cdot 7=280\) | Escribe los factores el mayor número de veces que aparecen en cualquiera de las factorizaciones y se multiplican. |
El múltiplo menos común de 28 y 40 es 280.
Encuentra el mínimo común múltiplo de 12 y 80.
- 240
- 120
- 960
- 480
- Contestar
-
- Correcto. \(\ 2 \cdot 2 \cdot 2 \cdot 2 \cdot 3 \cdot 5=240\)
- Incorrecto. 120 no es múltiplo de 80. La respuesta correcta es 240.
- Incorrecto. 960 es un múltiplo común, pero no es el mínimo común múltiplo. La respuesta correcta es 240.
- Incorrecto. 480 es un múltiplo común pero no es el mínimo común múltiplo. La respuesta correcta es 240.
Encontrar denominadores menos comunes
Se puede utilizar el mínimo común múltiplo de dos denominadores como mínimo común denominador para esas fracciones. Después reescribes cada fracción usando el mismo denominador.
El siguiente ejemplo muestra cómo usar el mínimo común múltiplo como mínimo común denominador.
Reescribir las fracciones\(\ \frac{2}{3}\) y\(\ \frac{1}{2}\) como fracciones con mínimo denominador común.
Solución
|
Los múltiplos de 3 incluyen 3, 6, 9, 12 Los múltiplos de 2 incluyen 2, 4, 6 6 es el mínimo denominador común. |
Encuentra el múltiplo menos común de los denominadores. Este es el mínimo denominador común. |
| \(\ \frac{2}{3} \cdot \frac{2}{2}=\frac{4}{6}\) | Reescribir\(\ \frac{2}{3}\) con un denominador de 6. |
| \(\ \frac{1}{2} \cdot \frac{3}{3}=\frac{3}{6}\) | Reescribir\(\ \frac{1}{2}\) con un denominador de 6. |
La fracción se\(\ \frac{2}{3}\) puede reescribir como\(\ \frac{4}{6}\).
La fracción se\(\ \frac{1}{2}\) puede reescribir como\(\ \frac{3}{6}\).
Encuentra el mínimo denominador común. Entonces expresar cada fracción usando el mínimo denominador común:\(\ \frac{3}{4}\) y\(\ \frac{1}{6}\).
- \(\ \frac{18}{24}, \frac{4}{24}\)
- \(\ \frac{3}{12}, \frac{1}{12}\)
- \(\ 24\)
- \(\ \frac{9}{12}, \frac{2}{12}\)
- Contestar
-
- Incorrecto. 24 es un denominador común, pero no el mínimo común denominador para las fracciones. La respuesta correcta es\(\ \frac{9}{12}\),\(\ \frac{2}{12}\).
- Incorrecto. 12 es el mínimo denominador común, pero estas fracciones no son equivalentes a las fracciones originales. Los numeradores son incorrectos. La respuesta correcta es\(\ \frac{9}{12}\),\(\ \frac{2}{12}\).
- Incorrecto. Se trata de un múltiplo de los denominadores, pero la tarea era reescribir las fracciones con un denominador común. La respuesta correcta es\(\ \frac{9}{12}\),\(\ \frac{2}{12}\).
- Correcto. \(\ \frac{3}{4} \cdot \frac{3}{3}=\frac{9}{12}\),\(\ \frac{1}{6} \cdot \frac{2}{2}=\frac{2}{12}\).
Sumando fracciones con denominadores diferentes
Para agregar fracciones con denominadores diferentes, primero reescribirlas con denominadores similares. Entonces, ¡ya sabes qué hacer! A continuación se muestran los pasos.
- Encuentra un denominador común.
- Reescribe cada fracción usando el denominador común.
- Ahora que las fracciones tienen un denominador común, se pueden sumar los numeradores.
- Simplifica a términos más bajos, expresando fracciones impropias como números mixtos.
Siempre se puede encontrar un denominador común multiplicando los dos denominadores juntos. Vea el ejemplo a continuación.
| \(\ \frac{2}{3}+\frac{1}{5}\) | Agregar. Simplifica la respuesta. |
Solución
| \(\ 3 \cdot 5=15\) | Como los denominadores no son iguales, encuentra un denominador común multiplicando los denominadores. |
|
\(\ \frac{2}{3} \cdot \frac{5}{5}=\frac{10}{15}\) \(\ \frac{1}{5} \cdot \frac{3}{3}=\frac{3}{15}\) |
Reescribe cada fracción con un denominador de 15. |
| \(\ \frac{10}{15}+\frac{3}{15}=\frac{13}{15}\) | Sumar las fracciones sumando los numeradores y manteniendo igual el denominador. Asegúrese de que la fracción no se pueda simplificar. |
\(\ \frac{2}{3}+\frac{1}{5}=\frac{13}{15}\)
Se puede encontrar un denominador común encontrando los múltiplos comunes de los denominadores. El múltiplo menos común es el más fácil de usar.
| \(\ \frac{3}{7}+\frac{2}{21}\) | Agregar. Simplifica la respuesta. |
Solución
|
Los múltiplos de 7 incluyen 7, 14, 21 Los múltiplos de 21 incluyen 21 |
Dado que los denominadores no son iguales, encuentra el mínimo denominador común encontrando el múltiplo menos común (LCM) de 7 y 21. |
|
\(\ \frac{3}{7} \cdot \frac{3}{3}=\frac{9}{21}\) \(\ \frac{2}{21}\) |
Reescribe cada fracción con un denominador de 21. |
| \(\ \frac{9}{21}+\frac{2}{21}=\frac{11}{21}\) | Sumar las fracciones sumando los numeradores y manteniendo igual el denominador. Asegúrese de que la fracción no se pueda simplificar. |
\(\ \frac{3}{7}+\frac{2}{21}=\frac{11}{21}\)
También puedes agregar más de dos fracciones siempre y cuando primero encuentres un denominador común para todas ellas. A continuación se muestra un ejemplo de una suma de tres fracciones. En este ejemplo, utilizará el método de factorización prima para encontrar el LCM.
| \(\ \frac{3}{4}+\frac{1}{6}+\frac{5}{8}\) | Agregar. Simplifica la respuesta y escribe como un número mixto. |
Solución
|
\ (\\ begin {array} {l} LCM:\(\ 2 \cdot 2 \cdot 2 \cdot 3=24\) |
Dado que los denominadores no son iguales, encuentra el mínimo denominador común encontrando el mínimo común múltiplo (LCM) de 4, 6 y 8. |
| \ (\\ begin {array} {l} \ frac {3} {4}\ cdot\ frac {6} {6} =\ frac {18} {24}\ \ frac {1} {6}\ cdot\ frac {4} {4} =\ frac {4} {24}\ \ frac {5} {8}\ cdot\ frac {3}} {3} =\ frac {15} {24} \ end {array}\) |
Reescribe cada fracción con un denominador de 24. |
| \(\ \frac{18}{24}+\frac{4}{24}+\frac{15}{24}=\frac{37}{24}\) | Sumar las fracciones sumando los numeradores y manteniendo igual el denominador. |
| \(\ \frac{37}{24}=1 \frac{13}{24}\) | Escribe la fracción impropia como número mixto y simplifica la fracción impropia. |
\(\ \frac{3}{4}+\frac{1}{6}+\frac{5}{8}=1 \frac{13}{24}\)
\(\ \frac{2}{3}+\frac{4}{5}+\frac{1}{12}\)Agregar. Simplifica la respuesta y escribe como un número mixto.
- \(\ 1 \frac{33}{60}\)
- \(\ 1 \frac{11}{20}\)
- \(\ \frac{31}{20}\)
- \(\ \frac{7}{20}\)
- Contestar
-
- Incorrecto. La fracción en el número mixto se puede simplificar. La respuesta correcta es\(\ 1 \frac{11}{20}\).
- Correcto. \(\ \frac{40}{60}+\frac{48}{60}+\frac{5}{60}=\frac{93}{60}=1 \frac{33}{60}=1 \frac{11}{20}\).
- Incorrecto. Expresar la fracción impropia como un número mixto. La respuesta correcta es\(\ 1 \frac{11}{20}\).
- Incorrecto. Encuentre un denominador común; exprese cada fracción usando el denominador común; agregue los numeradores y simplifique. La respuesta correcta es\(\ 1 \frac{11}{20}\).
Adición de números mixtos
Así como puedes agregar números enteros y fracciones propias, también puedes agregar números mixtos. Para sumar números mixtos, sumar los números enteros y las partes de fracción de los números mixtos juntos y luego recombinar para expresar el valor como un número mixto. Los pasos para sumar dos números mixtos se muestran en los siguientes ejemplos.
Puedes mantener juntos los números enteros y las fracciones usando un método vertical para sumar números mixtos como se muestra a continuación.
| \(\ 2 \frac{1}{8}+3 \frac{3}{8}\) | Agregar. Simplifica la respuesta y escribe como un número mixto. |
Solución
| \ (\\ begin {array} {r} 2\ frac {1} {8}\\ +3\ frac {3} {8}\ \ hline \ end {array}\) |
Organice los números mixtos verticalmente para que los números enteros se alineen y las fracciones se alineen. |
| \ (\\ begin {array} {r} 2\ frac {1} {8}\\ +3\ frac {3} {8}\ \ hline 5\ frac {4} {8} \ end {array}\) |
Sumar números enteros. Agrega fracciones. |
| \(\ 5 \frac{4}{8}=5 \frac{1}{2}\) | Simplifica la fracción. |
\(\ 2 \frac{1}{8}+3 \frac{3}{8}=5 \frac{1}{2}\)
Al sumar números mixtos, es posible que también necesites encontrar primero un denominador común. Considera el siguiente ejemplo.
| \(\ 8 \frac{5}{6}+7 \frac{4}{9}\) | Agregar. Simplifica la respuesta y escribe como un número mixto. |
Solución
|
Los múltiplos de 6 incluyen 6, 12, 18 Los múltiplos de 9 incluyen 9, 18 |
Encuentra un mínimo denominador común para las fracciones. |
| \ (\\ begin {array} {l} \ frac {5} {6}\ cdot\ frac {3} {3} =\ frac {15} {18}\ \ frac {4} {9}\ cdot\ frac {2} {2} =\ frac {8} {18} \ end {array}\) |
Exprese cada fracción con un denominador de 18. |
| \ (\\ begin {array} {r} 8\ frac {15} {18}\\ +7\ frac {8} {18}\ \ hline \ end {array}\) |
Organice los números mixtos verticalmente para que los números enteros se alineen y las fracciones se alineen. |
| \ (\\ begin {array} {r} 8\ frac {15} {18}\\ +7\ frac {8} {18}\ \ hline 15\ frac {23} {18} \ end {array}\) |
Sumar números enteros. Agrega fracciones. |
| \(\ \frac{23}{18}=1 \frac{5}{18}\) | Escribe la fracción impropia como un número mixto. |
|
\(\ 15+1+\frac{5}{18}\) \(\ 16 \frac{5}{18}\) |
Combina números enteros y fracción para escribir un número mixto. |
\(\ 8 \frac{5}{6}+7 \frac{4}{9}=16 \frac{5}{18}\)
\(\ 3 \frac{3}{5}+1 \frac{4}{9}\)Agregar. Simplifica la respuesta y escribe como un número mixto.
- \(\ \frac{2}{45}\)
- \(\ 5 \frac{2}{45}\)
- \(\ 4 \frac{1}{2}\)
- \(\ 4 \frac{47}{45}\)
- Responder
-
- Incorrecto. También se deben sumar los números enteros. La respuesta correcta es\(\ 5 \frac{2}{45}\).
- Correcto. \(\ 3+1+\frac{3}{5}+\frac{4}{9}\),\(\ 4+\frac{27}{45}+\frac{20}{45}=4+\frac{47}{45}=4+1 \frac{2}{45}=5 \frac{2}{45}\).
- Incorrecto. Para sumar fracciones con denominadores distintos, primero hay que encontrar un denominador común. La respuesta correcta es\(\ 5 \frac{2}{45}\).
- Incorrecto. Un número mixto simplificado es un número entero y una fracción propia. La respuesta correcta es\(\ 5 \frac{2}{45}\).
Adición de fracciones para resolver problemas
Saber sumar fracciones es útil en una variedad de situaciones. Al leer problemas, busca frases que te ayuden a saber que quieres sumar las fracciones.
En la parte superior de un libro se coloca una pila de panfletos. Si la pila de panfletos tiene\(\ 3 \frac{1}{4}\) pulgadas de grosor y el libro tiene\(\ 5 \frac{3}{4}\) pulgadas de grosor, ¿qué tan alto es el montón?
Solución
| \(\ 3 \frac{1}{4}+5 \frac{3}{4}\) | Encuentra la altura total de la pila añadiendo los espesores de la pila de panfletos y el libro. |
| \(\ 3+5+\frac{1}{4}+\frac{3}{4}\) | Agrupe los números enteros y las fracciones para facilitar la adición. |
| \(\ 8+\frac{1}{4}+\frac{3}{4}\) | Sumar números enteros. |
| \(\ \frac{1}{4}+\frac{3}{4}=\frac{4}{4}=1\) | Agrega fracciones. |
| \(\ 8+1=9\) | Combina número entero y fracción. |
El pilote mide 9 pulgadas de alto.
Una receta de pastel requiere\(\ 2 \frac{1}{4}\) tazas de leche y\(\ 1 \frac{1}{2}\) tazas de mantequilla derretida. Si estos son los únicos líquidos, ¿cuánto líquido hay en la receta?
Solución
| \(\ 2 \frac{1}{4}+1 \frac{1}{2}\) | Encuentra la cantidad total de líquido agregando las cantidades. |
| \(\ 2+1+\frac{1}{4}+\frac{1}{2}\) | Agrupe los números enteros y las fracciones para facilitar la adición. |
| \(\ 3+\frac{1}{4}+\frac{1}{2}\) | Sumar números enteros. |
| \(\ 3+\frac{1}{4}+\frac{2}{4}=3+\frac{3}{4}\) | Agrega fracciones. Recordemos eso\(\ \frac{1}{2}=\frac{2}{4}\). |
| \(\ 3 \frac{3}{4}\) | Combina número entero y fracción. |
Hay\(\ 3 \frac{3}{4}\) tazas de líquido en la receta.
¿Cuál es la precipitación total en un periodo de tres días si llueve\(\ 3 \frac{1}{4}\) pulgadas el primer día,\(\ \frac{3}{8}\) pulgada el segundo día y\(\ 2 \frac{1}{2}\) pulgadas en el tercer día?
- \(\ 6\)pulgadas
- \(\ 6 \frac{1}{8}\)pulgadas
- \(\ 5 \frac{1}{8}\)pulgadas
- \(\ 5 \frac{9}{8}\)pulgadas
- Responder
-
- Incorrecto. La respuesta no es un número entero porque las fracciones tienen una suma de\(\ \frac{9}{8}\). La respuesta correcta es\(\ 6 \frac{1}{8}\) pulgadas.
- Correcto. \(\ 5 \frac{9}{8}=6 \frac{1}{8}\)pulgadas.
- Incorrecto. Cuando agregas las fracciones obtienes\(\ 5+\frac{9}{8}\). El\(\ 5+\frac{9}{8}\) alambique contiene una fracción impropia. El\(\ \frac{9}{8}\) necesita ser cambiado\(\ 1 \frac{1}{8}\) y luego recombinado con el 5. Es necesario combinar el 1 del\(\ 1 \frac{1}{8}\) con el 5 para conseguir\(\ 6 \frac{1}{8}\), no\(\ 5 \frac{1}{8}\). La respuesta correcta es\(\ 6 \frac{1}{8}\).
- Incorrecto. \(\ 5 \frac{9}{8}\)no es el número mixto correcto; la parte fraccionaria del número sigue siendo impropia. La respuesta correcta es\(\ 6 \frac{1}{8}\).
Resumen
Sumar fracciones con denominadores similares implica sumar los numeradores y mantener el denominador igual. Siempre simplifique la respuesta. Para sumar fracciones con denominadores diferentes, primero encuentra un denominador común. El denominador menos común es más fácil de usar. El mínimo común múltiplo puede ser utilizado como mínimo común denominador. Agregar números mixtos implica sumar las partes fraccionarias, sumar los números enteros y luego recombinarlos como un número mixto.


