2.3.2: Restar fracciones y números mixtos
- Page ID
- 111419
- Restar fracciones con denominadores similares y diferentes.
- Restar números mixtos sin reagruparse.
- Restar números mixtos con reagrupamiento.
- Resolver problemas de aplicación que requieran la resta de fracciones o números mixtos.
Introducción
A veces se requiere la resta, más que la suma, para resolver problemas que involucran fracciones. Supongamos que estás haciendo panqueques y necesitas\(\ 4 \frac{1}{2}\) tazas de harina pero solo tienes\(\ 2 \frac{3}{4}\) tazas. ¿Cuántas tazas adicionales tendrás que conseguir para hacer los panqueques? Se puede resolver este problema restando los números mixtos.
Restar fracciones
Los problemas de resta de fracciones más simples son aquellos que tienen dos fracciones propias con un denominador común. Es decir, cada denominador es el mismo. El proceso es tal como es para la suma de fracciones con denominadores similares, ¡excepto que restas! Se resta el segundo numerador del primero y se mantiene igual el denominador.
Imagina que tienes un pastel con piezas de igual tamaño. Parte del pastel ya se ha comido, así que te queda una fracción del pastel. Podrías representar las piezas de pastel con la imagen de abajo.
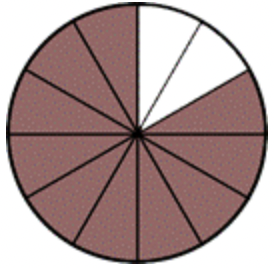
El pastel se corta en 12 trozos iguales para comenzar. Se comen dos, por lo que el pastel restante se puede representar con la fracción\(\ \frac{10}{12}\). Si se comen 3 trozos más de pastel, ¿qué fracción del pastel queda? Se puede representar ese problema con la expresión\(\ \frac{10}{12}-\frac{3}{12}\).
Si restas 3 piezas, puedes ver a continuación la\(\ \frac{7}{12}\) de los restos del pastel.
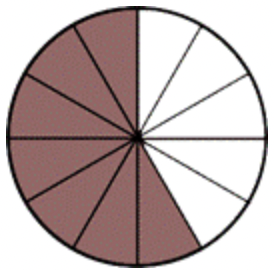
Puedes resolver este problema sin la imagen restando los numeradores y manteniendo el denominador igual:
\(\ \frac{10}{12}-\frac{3}{12}=\frac{7}{12}\)
Si los denominadores (fondos) de las fracciones son iguales, restar los numeradores (tops) y mantener el denominador igual. Recuerde simplificar la fracción resultante, si es posible.
| \(\ \frac{6}{7}-\frac{1}{7}\) | Restar. |
Solución
| \(\ \frac{6-1}{7}=\frac{5}{7}\) | Ambas fracciones tienen un denominador de 7, así que resta los numeradores y mantén el mismo denominador. |
\(\ \frac{6}{7}-\frac{1}{7}=\frac{5}{7}\)
| \(\ \frac{5}{9}-\frac{2}{9}\) | Restar. Simplifica la respuesta. |
Solución
| \(\ \frac{5}{9}-\frac{2}{9}=\frac{3}{9}\) | Las fracciones tienen un denominador similar, también conocido como denominador común, así que resta los numeradores. |
| \(\ \frac{3 \div 3}{9 \div 3}=\frac{1}{3}\) | Simplifica la fracción. |
\(\ \frac{5}{9}-\frac{2}{9}=\frac{1}{3}\)
Si los denominadores no son los mismos (tienen denominadores diferentes), primero debes reescribir las fracciones con un denominador común. El denominador menos común, que es el múltiplo menos común de los denominadores, es la elección más eficiente, pero cualquier denominador común servirá. Asegúrate de revisar tu respuesta para asegurarte de que esté en la forma más simple. Puedes usar la factorización de primos para encontrar el mínimo común múltiplo (MCM), que será el mínimo común denominador (LCD). Vea el ejemplo a continuación.
| \(\ \frac{1}{5}-\frac{1}{6}\) | Restar. Simplifica la respuesta. |
Solución
| \(\ 5 \cdot 6=30\) | Las fracciones tienen denominadores distintos, por lo que hay que encontrar un denominador común. Recordemos que se puede encontrar un denominador común multiplicando los dos denominadores juntos. |
|
\(\ \frac{1}{5} \cdot \frac{6}{6}=\frac{6}{30}\) \(\ \frac{1}{6} \cdot \frac{5}{5}=\frac{5}{30}\) |
Reescribe cada fracción como una fracción equivalente con un denominador de 30. |
| \(\ \frac{6}{30}-\frac{5}{30}=\frac{1}{30}\) | Restar los numeradores. Simplifique la respuesta si es necesario. |
\(\ \frac{1}{5}-\frac{1}{6}=\frac{1}{30}\)
El siguiente ejemplo muestra el uso de múltiplos para encontrar el múltiplo menos común, que será el mínimo denominador común.
| \(\ \frac{5}{6}-\frac{1}{4}\) | Restar. Simplifica la respuesta. |
Solución
|
Los múltiplos de 6 incluyen 6, 12, 18, 24 Los múltiplos de 4 incluyen 4, 8, 12, 16, 20 |
Encuentra el múltiplo menos común de los denominadores. |
| 12 es el múltiplo menos común de 6 y 4. | Este es el mínimo denominador común. |
| \ (\\ begin {array} {l} \ frac {5} {6}\ cdot\ frac {2} {2} =\ frac {10} {12}\ \ frac {1} {4}\ cdot\ frac {3} {3} =\ frac {3} {12} \ end {array}\) |
Reescribe cada fracción con un denominador de 12. |
| \(\ \frac{10}{12}-\frac{3}{12}=\frac{7}{12}\) | Restar las fracciones. Simplifique la respuesta si es necesario. |
\(\ \frac{5}{6}-\frac{1}{4}=\frac{7}{12}\)
\(\ \frac{2}{3}-\frac{1}{6}\)Restar y simplificar la respuesta.
- \(\ \frac{1}{3}\)
- \(\ \frac{3}{6}\)
- \(\ \frac{5}{6}\)
- \(\ \frac{1}{2}\)
- Contestar
-
- Incorrecto. Encuentra un mínimo denominador común y resta; luego simplifica. La respuesta correcta es\(\ \frac{1}{2}\).
- Incorrecto. Simplifica la fracción. La respuesta correcta es\(\ \frac{1}{2}\).
- Incorrecto. Restar, no sumar, las fracciones. La respuesta correcta es\(\ \frac{1}{2}\)
- Correcto. \(\ \frac{4}{6}-\frac{1}{6}=\frac{3}{6}=\frac{1}{2}\)
Restar números mixtos
Restar números mixtos funciona de la misma manera que sumar números mixtos. Para restar números mixtos, restar las partes del número entero de los números mixtos y luego restar las partes de fracción en los números mixtos. Por último, combine la respuesta del número entero y la respuesta de fracción para expresar la respuesta como un número mixto.
| \(\ 6 \frac{4}{5}-3 \frac{1}{5}\) | Restar. Simplifica la respuesta y escribe como un número mixto. |
Solución
|
\(\ 6-3=3\) \(\ \frac{4}{5}-\frac{1}{5}=\frac{3}{5}\) |
Restar los números enteros y restar las fracciones. |
| \(\ 3 \frac{3}{5}\) | Combina la fracción y el número entero. Asegúrese de que la fracción en el número mixto esté simplificada. |
\(\ 6 \frac{4}{5}-3 \frac{1}{5}=3 \frac{3}{5}\)
A veces puede ser más fácil expresar primero el número mixto como una fracción impropia y luego resolverlo. Considera el siguiente ejemplo.
| \(\ 8 \frac{1}{3}-4 \frac{2}{3}\) | Restar. Simplifica la respuesta y escribe como un número mixto. |
Solución
|
\(\ 8 \frac{1}{3}=\frac{8 \cdot 3+1}{3}=\frac{24+1}{3}=\frac{25}{3}\) \(\ 4 \frac{2}{3}=\frac{4 \cdot 3+2}{3}=\frac{12+2}{3}=\frac{14}{3}\) |
Escribe cada número mixto como una fracción impropia. |
| \(\ \frac{25}{3}-\frac{14}{3}=\frac{11}{3}\) | Dado que las fracciones tienen un denominador similar, resta los numeradores. |
| \(\ \frac{11}{3}=3 \frac{2}{3}\) | Escribe la respuesta como un número mixto. Divide 11 por 3 para obtener 3 con un resto de 2. |
\(\ 8 \frac{1}{3}-4 \frac{2}{3}=3 \frac{2}{3}\)
Dado que la suma es la operación inversa de resta, puede verificar su respuesta a un problema de resta con suma. En el ejemplo anterior, si agregas\(\ 4 \frac{2}{3}\) a tu respuesta de\(\ 3 \frac{2}{3}\), deberías obtener\(\ 8 \frac{1}{3}\).
\ (\\ begin {array} {r}
4\ frac {2} {3} +3\ frac {2} {3}\
4+3+\ frac {2} {3} +\ frac {2} {3} {3}\
7+\ frac {4} {3}\
7+1\ frac {1} {3}\
8\ frac {1} {3}
\ fin {matriz}\)
A veces hay que encontrar un denominador común para resolver un problema de resta de números mixtos.
| \(\ 7 \frac{1}{2}-2 \frac{1}{3}\) | Restar. Simplifica la respuesta y escribe como un número mixto. |
Solución
| \(\ 2 \cdot 3=6\) | Recordemos que un denominador común se puede encontrar fácilmente multiplicando los denominadores juntos. |
| \ (\\ begin {array} {l} \ frac {1} {2}\ cdot\ frac {3} {3} =\ frac {3} {6}\ \ frac {1} {3}\ cdot\ frac {2} {2} =\ frac {2} {6} \ end {array}\) |
Reescribe cada fracción usando el denominador común 6. |
| \(\ \frac{3}{6}-\frac{2}{6}=\frac{1}{6}\) | Restar las fracciones. |
| \(\ 7-2=5\) | Restar los números enteros. |
| \(\ 5 \frac{1}{6}\) | Combina el número entero y la fracción. |
\(\ 7 \frac{1}{2}-2 \frac{1}{3}=5 \frac{1}{6}\)
\(\ 9 \frac{4}{5}-4 \frac{2}{3}\)
Resta. Simplifica la respuesta y escríbala como un número mixto.
- \(\ \frac{2}{15}\)
- \(\ 5 \frac{2}{15}\)
- \(\ 4 \frac{7}{15}\)
- \(\ 5\)
- Contestar
-
- Incorrecto. Restar también los números enteros. La respuesta correcta es\(\ 5 \frac{2}{15}\).
- Correcto. \(\ 9-4=5\);\(\ \frac{4}{5}-\frac{2}{3}=\frac{12}{15}-\frac{10}{15}=\frac{2}{15}\). Combinarlos da\(\ 5 \frac{2}{15}\).
- Incorrecto. Restar, no sumar, las fracciones. La respuesta correcta es\(\ 5 \frac{2}{15}\).
- Incorrecto. Restar las fracciones así como los números enteros. La respuesta correcta es\(\ 5 \frac{2}{15}\).
Restar números mixtos con reagrupación
En ocasiones, al restar números mixtos, la parte fracción del segundo número mixto es mayor que la parte fracción del primer número. Considera el problema:\(\ 7 \frac{1}{6}-3 \frac{5}{6}\). El procedimiento estándar sería restar las fracciones, pero\(\ \frac{1}{6}-\frac{5}{6}\) resultaría en un número negativo. ¡No quieres eso! Puedes reagrupar uno de los números enteros del primer número, escribiendo el primer número mixto de una manera diferente:
\ (\\ begin {array} {l}
7\ frac {1} {6} =7+\ frac {1} {6} =6+1+\ frac {1} {6}\
6+\ frac {6} {6} +\ frac {1} {6} =6+\ frac {7} {6} =6\ frac {7} {6}
final {matriz}\)
Ahora, puedes escribir un problema equivalente al original:
\(\ 6 \frac{7}{6}-3 \frac{5}{6}\)
Entonces, simplemente restas como normalmente restas números mixtos:
\(\ 6-3=3\)
\(\ \frac{7}{6}-\frac{5}{6}=\frac{2}{6}=\frac{1}{3}\)
Entonces, la respuesta es\(\ 3 \frac{1}{3}\).
Al igual que con muchos problemas de fracciones, es posible que necesite encontrar un denominador común. ¡Recuerda que una parte clave para sumar y restar fracciones y números mixtos es asegurarte de tener un denominador común como primer paso! En el siguiente ejemplo, las fracciones originales no tienen un denominador similar. Necesitas encontrar uno antes de continuar con los siguientes pasos.
| \(\ 7 \frac{1}{5}-3 \frac{1}{4}\) | Restar. Simplifica la respuesta y escribe como un número mixto. |
Solución
|
Los múltiplos de 5 incluyen 5, 10, 15, 20, 25 Los múltiplos de 4 incluyen 4, 8, 12, 16, 20, 24 |
Encontrar un mínimo común denominador. 20 es el mínimo común múltiplo, así que úsalo para el mínimo común denominador. |
| \ (\\ begin {array} {l} \ frac {1} {5}\ cdot\ frac {4} {4} =\ frac {4} {20}\ \ frac {1} {4}\ cdot\ frac {5} {5} =\ frac {5} {20} \ end {array}\) |
Reescribe cada fracción usando el denominador común. |
| \(\ 7 \frac{4}{20}-3 \frac{5}{20}\) | Escribe la expresión usando los números mixtos con el denominador similar. |
| \ (\\ begin {array} {r} 7\ frac {4} {20} =6+1+\ frac {4} {20}\ 6+\ frac {20} {20} +\ frac {4} {20} {20}\ 6+\ frac {24} {20}\ 6\ frac {24} {20} \ end {array}\) |
Ya que la segunda fracción parte\(\ \frac{5}{20}\),, es mayor que la primera fracción,\(\ \frac{4}{20}\), reagrupa uno de los números enteros y escríbalo como\(\ \frac{20}{20}\). |
| \ (\\ begin {array} {l} 7\ frac {4} {20} -3\ frac {5} {20}\\ 6\ frac {24} {20} -3\ frac {5} {20} \ end {array}\) |
Reescribe la expresión de resta usando las fracciones equivalentes. |
| \ (\\ begin {array} {r} 6-3=3\ \ frac {24} {20} -\ frac {5} {20} =\ frac {19} {20} \ end {array}\) |
Restar los números enteros, restar las fracciones. |
| \(\ 3 \frac{19}{20}\) | Combina el número entero y la fracción. |
\(\ 7 \frac{1}{5}-3 \frac{1}{4}=3 \frac{19}{20}\)
A veces se resta un número mixto de un número entero. En este caso, también se puede reescribir el número entero como un número mixto para poder realizar la resta. Se utiliza un número mixto equivalente que tiene el mismo denominador que la fracción en el otro número mixto.
| \(\ 8-4 \frac{2}{5}\) | Restar. Simplifica la respuesta y escribe como un número mixto. |
Solución
| \ (\\ begin {array} {r} 8=7+1\\ 7+\ frac {5} {5}\\ 7\ frac {5} {5} \ end {array}\) |
Reagrupa uno del número entero y escríbalo como\(\ \frac{5}{5}\). |
| \(\ 7 \frac{5}{5}-4 \frac{2}{5}\) | Reescribe la expresión de resta usando las fracciones equivalentes. |
| \ (\\ begin {array} {l} 7-4=3\ \ frac {5} {5} -\ frac {2} {5} =\ frac {3} {5} \ end {array}\) |
Restar los números enteros, restar las fracciones. |
| \(\ 3 \frac{3}{5}\) | Combina el número entero y la fracción. |
\(\ 8-4 \frac{2}{5}=3 \frac{3}{5}\)
Si la parte fraccionaria del número mixto que se resta es mayor que la parte fraccionaria del número mixto del que se está restando, o si se está restando un número mixto de un número entero, siga estos pasos:
- Restar 1 del número entero, parte del número mixto que se está restando.
- Agrega ese 1 a la parte de fracción para hacer una fracción impropia. Por ejemplo:\(\ 7 \frac{2}{3}=6+\frac{3}{3}+\frac{2}{3}=6 \frac{5}{3}\)
- Después, restar como con cualquier otro número mixto.
Alternativamente, puede cambiar ambos números a fracciones impropias y luego restar.
\(\ 15-13 \frac{1}{4}\)Restar. Simplifica la respuesta y escribe como un número mixto.
- \(\ 2 \frac{1}{4}\)
- \(\ 28 \frac{1}{4}\)
- \(\ 1 \frac{3}{4}\)
- \(\ 2 \frac{3}{4}\)
- Contestar
-
- Incorrecto. Esta es la respuesta a\(\ 15 \frac{1}{4}-13\). La fracción tiene que restarse de los 15. La respuesta correcta es\(\ 1 \frac{3}{4}\).
- Incorrecto. Restar, no sumar, las cantidades. La respuesta correcta es\(\ 1 \frac{3}{4}\).
- Correcto. \(\ 14 \frac{4}{4}-13 \frac{1}{4}=1 \frac{3}{4}\)
- Incorrecto. Restar 1 del número entero al reescribirlo como un número mixto. La respuesta correcta es\(\ 1 \frac{3}{4}\).
Restar fracciones y números mixtos para resolver problemas
Saber restar fracciones y números mixtos es útil en una variedad de situaciones. Al leer problemas, busque palabras clave que indiquen que el problema se puede resolver usando la resta.
A Sherry le encanta colgarse, y con frecuencia compra tela que le gusta cuando la ve. Ella había comprado 5 yardas de tela con estampado azul y decidió usar\(\ 2 \frac{3}{8}\) yardas de ella en una colcha. ¿Cuánto de la tela con estampado azul le sobrará después de hacer la colcha?
Solución
| \(\ 5-2 \frac{3}{8}\) | Escribir una expresión usando resta para describir la situación. |
| \(\ 4 \frac{8}{8}-2 \frac{3}{8}\) | Reescribe el número entero como un número mixto. |
| \(\ 4 \frac{8}{8}-2 \frac{3}{8}=2 \frac{5}{8}\) | Resta. Verifique que el número mixto esté simplificado. |
Sherry tiene\(\ 2 \frac{5}{8}\) yardas de tela estampada azul sobrantes.
Pilar y Farouk están entrenando para un maratón. En un domingo reciente, ambos completaron una carrera. Farouk corrió\(\ 12 \frac{7}{8}\) millas y Pilar corrió\(\ 14 \frac{3}{4}\) millas. ¿Cuántas millas más corrió Pilar que Farouk?
Solución
| \(\ 14 \frac{3}{4}-12 \frac{7}{8}\) | Escribir una expresión usando resta para describir la situación. |
| \(\ 14 \frac{6}{8}-12 \frac{7}{8}\) | Reescribe los números mixtos usando el mínimo denominador común. |
| \ (\\ begin {array} {r} 14\ frac {6} {8}\\ 13+1+\ frac {6} {8} {8}\ 13+\ frac {8} {8} +\ frac {6} {8}\\ 13\ frac {14} {8} \ end {array}\) |
Dado que la parte fracción del segundo número mixto es mayor que la parte fracción del primer número mixto, reagrupe uno como fracción y reescribe el primer número mixto. |
| \(\ 13 \frac{14}{8}-12 \frac{7}{8}\) | Escribe la expresión de resta en su nueva forma. |
| \(\ 1 \frac{7}{8}\) | Resta. |
Pilar corrió\(\ 1 \frac{7}{8}\) millas más que Farouk.
Mike y José están pintando una habitación. José usó\(\ \frac{2}{3}\) una lata de pintura y Mike usó\(\ \frac{1}{2}\) una lata de pintura. ¿Cuánta pintura más usó José? Escribe la respuesta como una fracción de una lata.
Solución
| \(\ \frac{2}{3}-\frac{1}{2}\) | Escribir una expresión usando resta para describir la situación. |
| \ (\\ begin {array} {l} \ frac {2\ cdot 2} {3\ cdot 2} =\ frac {4} {6}\ \ frac {1\ cdot 3} {2\ cdot 3} =\ frac {3} {6} \ end {array}\) |
Reescribe las fracciones usando un denominador común. |
| \(\ \frac{4}{6}-\frac{3}{6}=\frac{1}{6}\) | Resta. Comprobar que la fracción esté simplificada. |
José usó\(\ \frac{1}{6}\) de una lata más pintura que Mike.
La planta de girasol de Mariah creció\(\ 18 \frac{2}{3}\) pulgadas en una semana. Su planta de tulipán creció\(\ 3 \frac{3}{4}\) pulgadas en una semana. ¿Cuántas pulgadas más creció el girasol en una semana que el tulipán?
- \(\ 22 \frac{5}{12}\)pulgadas
- \(\ 15 \frac{1}{12}\)pulgadas
- \(\ 15\)pulgadas
- \(\ 14 \frac{11}{12}\)pulgadas
- Contestar
-
- Incorrecto. Restar, no sumar, las fracciones. La respuesta correcta es\(\ 14 \frac{11}{12}\) pulgadas.
- Incorrecto. Restar\(\ \frac{2}{3}-\frac{3}{4}\), no\(\ \frac{3}{4}-\frac{2}{3}\). La respuesta correcta es\(\ 14 \frac{11}{12}\) pulgadas.
- Incorrecto. Restar las fracciones así como los números enteros en los números mixtos. La respuesta correcta es\(\ 14 \frac{11}{12}\) pulgadas.
- Correcto. \(\ 17 \frac{20}{12}-3 \frac{9}{12}=14 \frac{11}{12}\)
Resumen
Restar fracciones y números mixtos combina algunas de las mismas habilidades que sumar números enteros y sumar fracciones y números mixtos. Al restar fracciones y números mixtos, primero encuentra un denominador común si los denominadores no son iguales, reescribe cada fracción usando el denominador común, y luego restar los numeradores. Al restar números mixtos, si la fracción en el segundo número mixto es mayor que la fracción en el primer número mixto, reescriba el primer número mixto reagrupando un todo como fracción. Alternativamente, reescribir todas las fracciones como fracciones impropias y luego restar. Este proceso también se utiliza al restar un número mixto de un número entero.