3.1.1: Decimales y Fracciones
- Page ID
- 111434
- Leer y escribir números en notación decimal.
- Escribe decimales como fracciones.
- Escribe fracciones como decimales.
Introducción
Además de la notación de fracciones, la notación decimal es otra forma de escribir números entre 0 y 1. Los decimales también se pueden usar para escribir números entre dos números enteros cualesquiera. Por ejemplo, puede que tengas que escribir un cheque por $2,003.38. O, al medir la longitud de una habitación, puede encontrar que la longitud está entre dos números enteros, como 35.24 pies. En este tema, te enfocarás en leer y escribir números decimales, y reescribirlos en notación de fracciones.
Para leer o escribir números escritos en notación decimal, es necesario conocer el valor posicional de cada dígito, es decir, el valor de un dígito en función de su posición dentro de un número. Con números decimales, la posición de un numeral en relación con el punto decimal determina su valor posicional. Por ejemplo, el valor posicional del 4 en 45.6 está en el lugar de las decenas, mientras que el valor posicional de 6 en 45.6 está en el décimo lugar.
Notación decimal
Los números decimales son números cuyos valores posicionales se basan en 10s. Los números enteros son en realidad números decimales que son mayores o iguales a cero. El gráfico del valor posicional se puede extender para incluir números menores a uno, que a veces se denominan fracciones decimales. Se utiliza un punto decimal para separar la parte del número entero del número y la parte de fracción del número.
Digamos que estás midiendo la longitud de un camino de entrada y descubres que mide 745 pies. Diría usted este número como setecientos cuarenta y cinco. Entonces, una medición más precisa muestra que es 745.36 pies. Coloquemos este número en un gráfico de valor posicional.
Lo que se quiere examinar ahora son los valores posicionales de la parte decimal, que son los números 3 y 6 en el gráfico de abajo.
| Números decimales | Cientos | Decenas | Ones | Punto decimal | Décimas | centésimas |
| 745.36 | 7 | 4 | 5 | . | 3 | 6 |
Observe cómo los nombres de los topónimos comienzan desde el punto decimal. A la izquierda del punto decimal están los lugares unos, decenas y cientos, donde pones dígitos que representan números enteros que son mayores o iguales a cero. A la derecha del punto decimal están las décimas y centésimas, donde pones dígitos que representan números que son partes fraccionarias de uno, números que son más de cero y menores de uno.
Nuevamente, el valor posicional de un número depende de qué tan lejos esté del punto decimal. Esto es evidente en el gráfico a continuación, donde cada número tiene el dígito “4" ocupando un valor posicional diferente.
| Números decimales | Miles | Cientos | Decenas | Ones | Punto decimal | Décimas | centésimas | Milésimas |
| 0.004 | 0 | . | 0 | 0 | 4 | |||
| 0.04 | 0 | . | 0 | 4 | ||||
| 0.4 | 0 | . | 4 | |||||
| 4 | 4 | . | ||||||
| 40 | 4 | 0 | . | |||||
| 400 | 4 | 0 | 0 | . | ||||
| 4000 | 4 | 0 | 0 | 0 | . |
Imagínese que a medida que un globo grande se desinfla, el volumen de aire en su interior va de 1,000 litros, a 100 litros, a 10 litros, a 1 litro. Observe que está dividiendo un valor posicional entre diez a medida que va hacia la derecha. Divides 100 por 10 para llegar al lugar de las decenas. Esto se debe a que hay 10 decenas en 100. Entonces, divides 10 por 10 para llegar al lugar de unos, porque hay 10 en 10.
Ahora, supongamos que el globo sigue perdiendo volumen, pasando de 1 litro, a 0.1 litros, a 0.01 litros, y luego a 0.001 litros. Observe que continúa dividiendo por 10 cuando se mueve a decimales. Divides 1 por\(\ 10\left(\frac{1}{10}\right)\) para llegar al décimo lugar, que básicamente es romper uno en 10 pedazos. Y para llegar al lugar de los cientos, se rompe el décimo en diez pedazos más, lo que resulta en la fracción\(\ \frac{1}{100}\). La relación entre los decimales y las fracciones se captura en la siguiente tabla.
| Forma de Word | Notación decimal | Notación de Fracciones |
| mil | 1,000 | \(\ \frac{1,000}{1}\) |
| cien | 100 | \(\ \frac{100}{1}\) |
| diez | 10 | \(\ \frac{10}{1}\) |
| uno | 1 | \(\ \frac{1}{1}\) |
| una décima | 0.1 | \(\ \frac{1}{10}\) |
| centésima | 0.01 | \(\ \frac{1}{100}\) |
| milésima | 0.001 | \(\ \frac{1}{1,000}\) |
Considera un número con más dígitos. Supongamos que un pescador tiene una red llena de peces que pesa 1,357.924 kilogramos. Para escribir este número, es necesario utilizar el lugar de miles, que está conformado por 10 cientos. También usas el lugar milésimas, que es\(\ \frac{1}{10}\) de centésima. En otras palabras, hay diez milésimas en una centésima.
| Números decimales | no th lado | th lado | ||||||
| Miles | Cientos | Decenas | Ones | Punto decimal | Décimas | centésimas | Milésimas | |
| 1,357.924 | 1 | 3 | 5 | 7 | . | 9 | 2 | 4 |
Como puede ver, pasar del punto decimal a la izquierda son unos, decenas, cientos, miles, etc. Este es el “no th lado”, que son los números mayores o iguales a uno. Pasar del punto decimal a la derecha son décimas, centésimas, milésimas. Este es el “lado th”, que son los números menores que 1.
1,357.924
no th lado th lado
El patrón que va a la derecha o a la izquierda desde el punto decimal es el mismo, pero hay dos grandes diferencias:
- Los valores posicional a la derecha del punto decimal terminan en “th”.
- No existe tal cosa como “uno”. De tu trabajo con fracciones, sabes que 5 y\(\ \frac{5}{1}\) son lo mismo.
¿Cuál es el valor posicional de 8 en 4,279.386?
Solución
Escriba el número en un gráfico de valor posicional. Lee el valor del 8 del gráfico.
| Números decimales | no th lado | th lado | ||||||
| Miles | Cientos | Decenas | Ones | Punto decimal | Décimas | centésimas | Milésimas | |
| 4,279.386 | 4 | 2 | 7 | 9 | . | 3 | 8 | 6 |
En el número 4,279.386, el 8 está en el lugar centésimas.
¿Cuál es el valor posicional del 7 en 324.2671?
- miles
- milésimas
- cientos
- centésimas
- Contestar
-
- Incorrecto. El dígito 7 está a la derecha del punto decimal, lo que significa que es menor que uno y en el lado th. La respuesta correcta es milésimas.
- Correcto. El dígito 7 es de tres decimales a la derecha del punto decimal, lo que significa que está en el lugar milésimas.
- Incorrecto. El dígito 7 es de tres decimales a la derecha del punto decimal, lo que significa que está en el lugar milésimas.
- Incorrecto. El dígito 7 es de tres decimales a la derecha del punto decimal, lo que significa que está en el lugar milésimas.
Lectura de decimales
La forma más fácil de leer un número decimal es leer la parte de la fracción decimal como una fracción. (Sin embargo, no simplifique la fracción.) Supongamos que tienes 0.4 gramos de yogur en una taza. Dirías, “4 décimas de gramo de yogur”, ya que las 4 están en el lugar de las décimas.
Tenga en cuenta que el denominador de la fracción escrita en forma de fracción es siempre una potencia de diez, y el número de ceros en el denominador es el mismo que el número de decimales a la derecha del punto decimal. Consulte los ejemplos en la tabla a continuación para obtener más orientación.
| Notación decimal | Notación de Fracciones | Forma de Word |
| 0.5 | \(\ \frac{5}{10}\) | cinco décimas |
| 0.34 | \(\ \frac{34}{100}\) | treinta y cuatro centésimas |
| 0.896 | \(\ \frac{896}{1,000}\) | ochocientos noventa y seis milésimas |
Observe que 0.5 tiene una posición decimal. Su fracción equivalente,\(\ \frac{5}{10}\), tiene un denominador de 10—que es 1 seguido de uno cero. En general, cuando estás convirtiendo decimales en fracciones, el denominador es siempre 1, seguido del número de ceros que corresponden al número de decimales en el número original.
Otra forma de determinar qué número colocar en el denominador es usar el valor posicional del último dígito sin la parte “ths”. Por ejemplo, si el número es 1.458, el 8 está en el lugar milésimas. Quita los “ths” y tienes mil, así el número está escrito como\(\ 1 \frac{458}{1000}\).
Escribe 0.68 en forma de palabras.
Solución
| \(\ 0.68=\frac{68}{100}\)=sesenta y ocho centésimas |
Tenga en cuenta que el número se lee como una fracción. También tenga en cuenta que el denominador tiene 2 ceros, lo mismo que el número de decimales en el número original. |
El número 0.68 en forma de palabra es sesenta y ocho centésimas.
Recordemos que un número mixto es una combinación de un número entero y una fracción. En el caso de un decimal, un número mixto es también una combinación de un número entero y una fracción, donde la fracción se escribe como fracción decimal.
Para leer números mixtos, digamos la parte del número entero, la palabra “y” (que representa el punto decimal), y el número a la derecha del punto decimal, seguido del nombre y el valor posicional del último dígito. Esto se puede ver demostrado en el siguiente diagrama, en el que el último dígito se encuentra en el lugar de las diez milésimas.
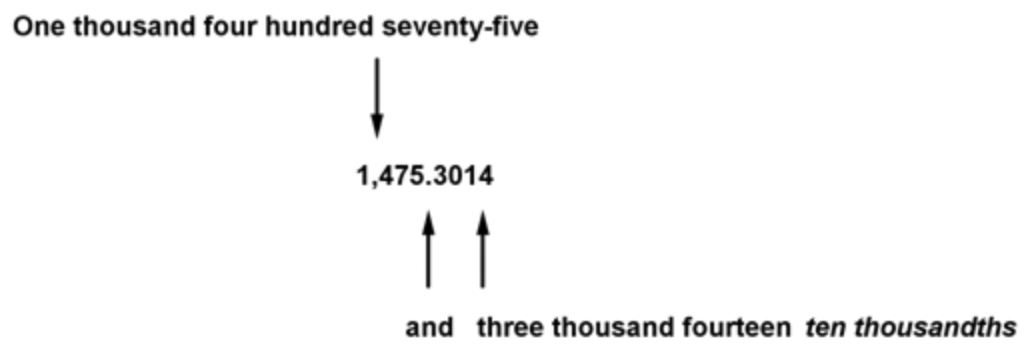
Otra forma de pensar sobre esto es con dinero. Supongamos que paga $15,264.25 por un auto. Leería esto como quince mil doscientos sesenta y cuatro dólares y veinticinco centavos. En este caso, los “centavos” significa “centésimas de dólar”, por lo que esto es lo mismo que decir quince mil, doscientos sesenta y cuatro y veinticinco centésimas. En la siguiente tabla se muestran algunos ejemplos más.
| Notación decimal | Notación de Fracciones | Forma de Word |
| 9.4 | \(\ 9 \frac{4}{10}\) | Nueve y cuatro décimas |
| 87.49 | \(\ 87 \frac{49}{100}\) | Ochenta y siete y cuarenta y nueve centésimas |
| 594.236 | \(\ 594 \frac{236}{1000}\) | Quinientos noventa y cuatro doscientos treinta y seis milésimas |
Escribe 4.379 en forma de palabras.
Solución
| \(\ 4.379=4 \frac{379}{1,000}\)= cuatrocientos setenta y nueve milésimas |
La fracción decimal se lee como una fracción. Tenga en cuenta que el denominador tiene 3 ceros, lo mismo que el número de decimales en el número original. |
El número 4.379 en forma de palabra es de cuatrocientos setenta y nueve milésimas.
Escribe 2.364 en forma de palabras.
- dos trescientos sesenta y cuatro centésimas
- dos trescientos sesenta y cuatro milésimas
- dos mil trescientos sesenta y cuatro
- trescientos sesenta y cuatro décimas y dos
- Contestar
-
- dos trescientos sesenta y cuatro centésimas
Incorrecto. Usted indicó el lugar decimal equivocado en su respuesta. La respuesta correcta es de doscientos sesenta y cuatro milésimas.
- Correcto. 2.364 es lo mismo que\(\ 2 \frac{364}{1,000}\), así que además del número entero 2, tienes trescientos sesenta y cuatro milésimas.
- Incorrecto. Ignoraste el punto decimal. La respuesta correcta es decimal; en este caso, doscientos sesenta y cuatro milésimas.
- Incorrecto. Usted indicó el lugar decimal equivocado en su respuesta, y la parte del número entero debe mencionarse antes de la parte decimal. La respuesta correcta es de doscientos sesenta y cuatro milésimas.
- dos trescientos sesenta y cuatro centésimas
Escribir decimales como fracciones simplificadas
Como has visto anteriormente, cada decimal puede escribirse como una fracción. Para convertir un decimal en una fracción, coloque el número después del punto decimal en el numerador de la fracción y coloque el número 10,100, o 1,000, u otra potencia de 10 en el denominador. Por ejemplo, 0.5 estaría escrito como\(\ \frac{5}{10}\). Notarás que esta fracción se puede simplificar aún más, ya que\(\ \frac{5}{10}\) reduce a\(\ \frac{1}{2}\), que es la respuesta final.
Familiaricémonos más con esta relación entre decimales y ceros en el denominador observando varios ejemplos. Observe que en cada ejemplo, el número de decimales es diferente.
Escribe 0.6 como una fracción simplificada.
Solución
| \(\ 0.6=\frac{6}{10}\) | El último decimal es décimas, así que usa 10 para tu denominador. El número de ceros en el denominador es siempre el mismo que el número de decimales en el decimal original. |
| \(\ \frac{6 \div 2}{10 \div 2}=\frac{3}{5}\) | Simplifica la fracción. |
\(\ 0.6=\frac{3}{5}\)
Veamos un ejemplo en el que un número con dos decimales se escribe como fracción.
Escribe 0.64 como fracción simplificada.
Solución
| \(\ 0.64=\frac{64}{100}\) | El último decimal es centésimas, así que usa 100 para tu denominador. El número de ceros en el denominador es siempre el mismo que el número de decimales en el decimal original. |
| \(\ \frac{64 \div 4}{100 \div 4}=\frac{16}{25}\) | Simplifica la fracción. |
\(\ 0.64=\frac{16}{25}\)
Ahora, examine cómo se hace esto en el siguiente ejemplo usando un decimal con dígitos en tres decimales.
Escribe 0.645 como fracción simplificada.
Solución
| \(\ 0.645=\frac{645}{1,000}\) | Tenga en cuenta que hay 3 ceros en el denominador, que es lo mismo que el número de decimales en el decimal original. |
| \(\ \frac{645 \div 5}{1,000 \div 5}=\frac{129}{200}\) | Simplifica la fracción. |
\(\ 0.645=\frac{129}{200}\)
Se puede escribir una fracción como decimal incluso cuando hay ceros a la derecha del punto decimal. Aquí un ejemplo en el que el único dígito mayor que cero está en el lugar milésimas.
Escribe 0.007 como fracción simplificada.
Solución
| \(\ 0.007=\frac{7}{1,000}\) |
Tenga en cuenta que 7 está en el lugar milésimas, por lo que escribe mil en el denominador. El número de ceros en el denominador es siempre el mismo que el número de decimales en el decimal original. La fracción no puede simplificarse más. |
\(\ 0.007=\frac{7}{1,000}\)
Al escribir decimales mayores a 1, solo necesitas cambiar la parte decimal a una fracción y mantener la parte entera del número. Por ejemplo, 6.35 se puede escribir como\(\ 6 \frac{35}{100}\).
Escribe 8.65 como fracción mixta simplificada.
Solución
| \(\ 8.65=8 \frac{65}{100}=8 \frac{13}{20}\) |
Reescribir 0.65 como\(\ \frac{65}{100}\). Tenga en cuenta que el número de ceros en el denominador es dos, que es lo mismo que el número de decimales en el decimal original. Luego simplifica\(\ \frac{65}{100}\) dividiendo el numerador y el denominador por 5. |
\(\ 8.65=8 \frac{13}{20}\)
Escribe 0.25 como una fracción.
- \(\ \frac{2}{5}\)
- \(\ \frac{1}{4}\)
- \(\ \frac{4}{1}\)
- \(\ \frac{5}{2}\)
- Contestar
-
- Incorrecto. Es posible que hayas puesto el dígito de las décimas lugar en el numerador, y el dígito de las centésimas colocar en el denominador. La respuesta correcta es\(\ \frac{1}{4}\).
- Correcto. El número 0.25 se puede escribir como\(\ \frac{25}{100}\), lo que reduce a\(\ \frac{1}{4}\).
- Incorrecto. Probablemente confundiste el numerador y el denominador. La respuesta correcta es\(\ \frac{1}{4}\).
- Incorrecto. Es posible que hayas puesto el dígito de las décimas lugar en el denominador, y el dígito de las centésimas en el numerador. La respuesta correcta es\(\ \frac{1}{4}\).
Escribir fracciones como decimales
Así como se puede escribir un decimal como fracción, cada fracción se puede escribir como decimal. Para escribir una fracción como decimal, divida el numerador (arriba) de la fracción por el denominador (abajo) de la fracción. Use división larga, si es necesario, y anote dónde colocar el punto decimal en tu respuesta. Por ejemplo, para escribir\(\ \frac{3}{5}\) como decimal, divida 3 por 5, lo que resultará en 0.6.
Escribir\(\ \frac{1}{2}\) como decimal.
Solución
| \ (\\ begin {array} {r} 0.5\\\\ 2\ longdiv {1.0}\\ -1.0\\ \ hline 0\ \ end {array}\) |
Usando división larga, se puede ver que dividir 1 por 2 da como resultado 0.5. |
\(\ \frac{1}{2}=0.5\)
Tenga en cuenta que también podría haber pensado en el problema así:\(\ \frac{1}{2}=\frac{?}{10}\), y luego resuelto para?. Una forma de pensar sobre este problema es que 10 es cinco veces mayor que 2, por lo que tendrá que ser cinco veces mayor que 1. ¿Qué número es cinco veces mayor que 1? Cinco es, entonces la solución es\(\ \frac{1}{2}=\frac{5}{10}\).
Ahora mira un ejemplo más complejo, donde el último dígito de la respuesta está en el lugar milésimas.
Escribir\(\ \frac{3}{8}\) como decimal.
Solución
| \ (\\ comenzar {matriz} {r} 0.375\\\\ 8\ longdiv {3.000}\\ -24\\\\\\\ hline 60\ \\\\ hline 60\\\\\\\ -56\\\\ \\ hline 40\\\\ -40\\\ \ hline 0\\ \ final {matriz}\) |
Usando división larga, se puede ver que dividir 3 por 8 da como resultado 0.375. |
\(\ \frac{3}{8}=0.375\)
La conversión de fracciones a decimales a veces da como resultado respuestas con números decimales que comienzan a repetirse. Por ejemplo,\(\ \frac{2}{3}\) convierte a 0.666, un decimal repetido, en el que el 6 se repite infinitamente. Escribirías esto como\(\ 0 . \overline{6}\), con una barra sobre el primer dígito decimal para indicar que las 6 repeticiones. Mira este ejemplo de un problema en el que se repiten dos dígitos consecutivos en la respuesta.
Convertir\(\ \frac{4}{11}\) a decimal.
Solución
| \ (\\ begin {array} {r} 0.3636\\\\ 11\ longdiv {4.0000}\\ -33\\\\\\\ \ hline 70\\\\\\ hline 70\ \\\\\\\\ \ hline 40\\\\\ -33\\\\ \ hline 70\\\ -66\\ \ hline 4\ \ final {array}\) |
Usando división larga, se puede ver que dividir 4 por 11 da como resultado 0.36 repetir. Como resultado, esto se escribe con una línea sobre él como\(\ 0 . \overline{36}\). |
\(\ \frac{4}{11}=0 . \overline{36}\)
Con números mayores a 1, mantenga la parte del número entero del número mixto como el número entero en el decimal. Luego usa la división larga para convertir la parte de la fracción a un decimal. Por ejemplo, se\(\ 2 \frac{3}{20}\) puede escribir como 2.15.
Convertir\(\ 2 \frac{1}{4}\) a decimal.
Solución
| \ (\\ begin {array} {r} 0.25\\\ 4\ longdiv {1.00}\\ -8\\\\ \ hline 20\\\ -20\\ \ hline 0\\ \ end {array}\\) |
Sabiendo que todo el número 2 seguirá siendo el mismo durante la conversión, enfocarse únicamente en la parte decimal. Usando división larga, se puede ver que dividir 1 por 4 da como resultado 0.25. |
| \(\ 2+0.25=2.25\) | Ahora trae de vuelta el número entero 2, y la fracción resultante es 2.25. |
\(\ 2 \frac{1}{4}=2.25\)
Para escribir una fracción como decimal, divida el numerador (arriba) de la fracción por el denominador (abajo) de la fracción.
En el caso de repetir decimales, escriba el dígito o dígitos repetidos con una línea sobre él. Por ejemplo, 0.333 repitiendo se escribiría como\(\ 0 . \overline{3}\).
Resumen
La notación decimal es otra forma de escribir números que son menores a 1 o que combinan números enteros con fracciones decimales, a veces llamados números mixtos. Cuando escribes números en notación decimal, puedes usar un gráfico de valor posicional extendido que incluya posiciones para números menores de uno. Puedes escribir números escritos en notación de fracciones (fracciones) en notación decimal (decimales), y puedes escribir decimales como fracciones. Siempre se puede convertir entre notación fraccionaria y notación decimal.


