3.1.2: Ordenar y redondear decimales

Última actualización
Guardar como PDF

Page ID: 111436

The NROC Project

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

Use una línea numérica para ayudar a comparar decimales.
Compara decimales, comenzando con sus dígitos de izquierda a derecha.
< or >Utilízalo para comparar decimales.
Redondea un decimal dado a un lugar especificado.

Introducción

Los números decimales son una combinación de números enteros y números entre números enteros. A veces es importante poder comparar decimales para saber cuál es mayor. Por ejemplo, si alguien corrió el guión de 100 metros en 10.57 segundos, y alguien más corrió la misma carrera en 10.67 segundos, puedes comparar los decimales para determinar qué tiempo es más rápido. Saber comparar decimales requiere una comprensión del valor decimal, y es similar a comparar números enteros.

Cuando se trabaja con decimales, hay momentos en los que no se necesita un número preciso. Cuando eso es cierto, redondear números decimales es útil. Por ejemplo, si la bomba de la gasolinera muestra que llenaste el auto de una amiga con 16.478 galones de gasolina, es posible que quieras redondear el número y simplemente decirle que lo llenaste con 16.5 galones.

Comparando decimales

Puedes usar una línea numérica para comparar decimales. El número que está más a la derecha es mayor. Examine este método en el siguiente ejemplo.

Ejemplo

< or >Utilízalo para [] para escribir una oración verdadera: 10.5 [] 10.7.

Solución

$Screen Shot 2021-04-26 en 2.55.06 PM.png$

Aquí, los dígitos en los décimos lugares difieren. Los números se trazan en una línea numérica que va de 10.0 a 11.0. Debido a que 10.5 está a la izquierda de 10.7 en la recta numérica, 10.5 es menor que (<) 10.7.

10.5 < 10.7

Otro enfoque para comparar decimales es comparar los dígitos en cada número, comenzando por el mayor valor posicionar, que está a la izquierda. Cuando un dígito en un número decimal es mayor que el dígito correspondiente en el otro número, entonces ese número decimal es mayor.

Por ejemplo, primero compara los décimos dígitos. Si son iguales, muévase al lugar de las centésimas. Si estos dígitos no son iguales, el decimal con el dígito mayor es el número decimal mayor. Observe cómo se hace esto en los ejemplos a continuación.

Ejemplo

< or >Utilízalo para [] para escribir una oración verdadera: 35.689 [] 35.679.

Solución

$Screen Shot 2021-04-26 en 2.58.40 PM.png$

Aquí, los números en las decenas, unos, y décimas lugares, 35.6, son los mismos. Sin embargo, los dígitos en los lugares centésimas difieren. Debido a que 8 es mayor que 7, 35.689 es mayor que 35.679.

35.689 > 35.679

Si más de dos dígitos en los dos números difieren, concéntrese en el dígito en el mayor valor positorio. Mira este ejemplo en el que se comparan dos sumas de dinero.

Ejemplo

< or >Utilízalo para [] para escribir una oración verdadera: $45.67 [] $45.76.

Solución

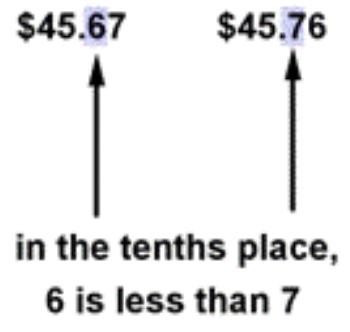
$Screen Shot 2021-04-26 en 3.04.47 PM.png$

Aquí, el valor posicionar que determina qué cantidad es mayor no es el lugar de las centésimas, sino las décimas. Debido a que 6 décimas son menos de 7 décimas, $45.67 son menos de 45.76 dólares.

$45.67 < $45.76

Si un número tiene más decimales que otro, puede usar 0s como marcadores de posición en el número con menos decimales para ayudarle a comparar. Por ejemplo, si estás comparando 4.75 y 4.7, te puede resultar útil escribir 4.7 como 4.70 para que cada número tenga tres dígitos. Tenga en cuenta que sumar este 0 extra no cambia el valor del decimal; usted está sumando 0 centésimas al número. Puede agregar marcadores de posición 0s siempre y cuando recuerde agregar los ceros al final del número, a la derecha del punto decimal.

Esto se demuestra en el siguiente ejemplo.

Ejemplo

< or >Utilízalo para [] para escribir una oración verdadera: 5.678 [] 5.6.

Solución

Aquí, puedes insertar dos ceros en los lugares centésimas y milésimas de 5.6 para que tengas el mismo número de dígitos para cada uno. Entonces, puedes comparar dígitos. Busque el mayor valor positorio que tenga diferentes valores en cada número. Aquí, es el lugar de las centésimas.

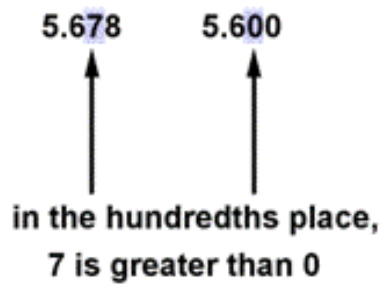
$Screen Shot 2021-04-26 at 3.28.57 PM.png$

Debido a que 7 es mayor que 0, 5.678 es mayor que 5.600.

5.678 > 5.6

Estrategias para comparar decimales

Usa una línea numérica para ayudar a comparar decimales, como hiciste con números enteros.
Compara decimales comenzando con sus dígitos de izquierda a derecha. Cuando dos dígitos no son iguales, el que tiene el dígito mayor es el número mayor.

Ejercicio

< or >Utilízalo para [] para escribir una oración verdadera: 45.675 [] 45.645.

45.675 < 45.645
45.675 > 45.645

Contestar

Incorrecto. Al comparar los dígitos en los lugares centésimas se observa que 7 es mayor que 4. Como resultado, 45.675 > 45.645.
Correcto. 45.675 > 45.645, porque el 7 en 45.675 es mayor que el 4 correspondiente en 45.645.

Redondeo de decimales

Redondear con decimales es como redondear con números enteros. Al igual que con los números enteros, redondea un número a un valor positorio dado. Todo a la derecha del valor positorio dado se convierte en un cero, y el dígito en el valor positorio dado o bien permanece igual o aumenta en uno.

Con decimales, puedes “soltar” los ceros al final de un número sin cambiar su valor. Por ejemplo, 0.20=0.2, como$\ \frac{20}{100}$ simplifica a$\ \frac{2}{10}$. Por supuesto, no se pueden soltar ceros antes del punto decimal:$\ 200 \neq 20$.

Los ceros que se producen al final de un número decimal se denominan ceros finales.

Dejar caer ceros con números enteros y decimales
Al soltar ceros al final de un número entero, se cambia el valor de un número.	$\ 7200 \neq 72$ $\ 200,000 \neq 2$
Dejar caer ceros al final de un decimal no cambia el valor del número.	$\ 36.00=36$ $\ 1.00000=1$

Una forma de pensarlo es considerar el número “treinta y seis dólares”. Esta cantidad se puede escribir igualmente bien de dos maneras:

$\ \$ 36=\$ 36.00$

Cualquier cero al final de un número decimal se puede eliminar:

18.25000=18.2500=18.250=18.25

Ejemplo

Un velocista corrió una carrera en 7.354 segundos. ¿Cuál era el tiempo del velocista, redondeado a la décima de segundo más cercana?

Solución

$\ 7.354$	Mira el primer dígito a la derecha del dígito décimo.
$\ 7.354 \rightarrow 7.400$	Desde 5=5, redondea el 3 hasta 4.
$\ 7.400$	Cambia todos los dígitos a la derecha del valor positorio dado a ceros. Este es un paso intermedio que en realidad no escribes.
$\ 7.4$	Desde 0.400=0.4, los ceros no son necesarios y deben bajarse.

7.354 redondeado a la décima más cercana es 7.4

En el ejemplo anterior, el dígito al lado del valor positorio seleccionado es 5, por lo que redondea hacia arriba. Veamos un caso en el que el dígito al lado del valor positorio seleccionado es menor que 5.

Ejemplo

Vuelta 7.354 a la centésima más cercana.

Solución

$\ 7.354$	Mira el primer dígito a la derecha del dígito centésimas.
$\ 7.354 \rightarrow 7.350$	Desde 4<5, dejar 5 como está.
$\ 7.35$	Los ceros a la derecha del valor positorio dado no son necesarios y deben ser dejados caer.

7.354 redondeado a la centésima más cercana es 7.35.

A veces se le pide redondear un número decimal a un valor posicionar que está en la parte del número entero. Recuerda que no puedes dejar caer ceros a la izquierda del punto decimal.

Ejemplo

Redondea 1,294.6374 al cien más cercano.

Solución

$\ 1,294.6374$

Mira el primer dígito a la derecha del lugar de los cientos.

$\ 1,294.6374 \rightarrow 1,300.000$

9 es mayor que 5, así redondea el 2 hasta 3.

$\ 1,300$

Deben incluirse los ceros a la izquierda del decimal.

Los ceros a la derecha del decimal se pueden soltar y deben caer.

1,294.6374 redondeado al cien más cercano es de 1,300.

Sugerencia sobre redondear decimales

Al redondear, todo a la derecha del valor positorio dado se convierte en un cero, y el dígito en el valor positorio dado permanece igual o redondea uno. Los ceros finales después del punto decimal deben dejarse caer.

Ejercicio

Vuelta 10.473 a la décima más cercana.

10.47
10.4
10.473
10.5

Contestar

Incorrecto. Redondeaste a la centésima más cercana, cuando deberías haber redondeado a la décima más cercana. La respuesta correcta es 10.5.
Incorrecto. Redondeaste hacia abajo cuando deberías haber redondeado hacia arriba. La respuesta correcta es 10.5.
Incorrecto. No redondeaste en absoluto este número. Si hubieras redondeado al décimo más cercano, habrías encontrado la respuesta correcta, 10.5.
Correcto. Redondeaste a la décima más cercana, y tenías razón para redondear hacia arriba, porque el 7 en 10.473 es mayor que 5.

Resumen

Ordenar, comparar y redondear decimales son habilidades importantes. Puede averiguar los tamaños relativos de dos números decimales usando líneas numérica y comparando los dígitos en el mismo valor posicionar de los dos números. Para redondear un decimal a un valor positorio específico, cambie todos los dígitos a la derecha del valor posicionar dado a cero, y luego redondear el dígito en el valor positorio dado, ya sea hacia arriba o hacia abajo. Los ceros finales después del punto decimal deben dejarse caer.

Al soltar ceros al final de un número entero, se cambia el valor de un número.	\(\ 7200 \neq 72\) \(\ 200,000 \neq 2\)
Dejar caer ceros al final de un decimal no cambia el valor del número.	\(\ 36.00=36\) \(\ 1.00000=1\)

\(\ 7.354\)	Mira el primer dígito a la derecha del dígito décimo.
\(\ 7.354 \rightarrow 7.400\)	Desde 5=5, redondea el 3 hasta 4.
\(\ 7.400\)	Cambia todos los dígitos a la derecha del valor positorio dado a ceros. Este es un paso intermedio que en realidad no escribes.
\(\ 7.4\)	Desde 0.400=0.4, los ceros no son necesarios y deben bajarse.

\(\ 7.354\)	Mira el primer dígito a la derecha del dígito centésimas.
\(\ 7.354 \rightarrow 7.350\)	Desde 4<5, dejar 5 como está.
\(\ 7.35\)	Los ceros a la derecha del valor positorio dado no son necesarios y deben ser dejados caer.