4.1.1: Simplificación de Ratios y Tarifas

Objetivos de aprendizaje

• Escribe relaciones y tasas como fracciones en forma más simple.
• Encuentra tarifas unitarias.
• Encuentra precios unitarios.

Introducción

Los ratios se utilizan para comparar cantidades o cantidades o describir una relación entre dos cantidades o cantidades. Por ejemplo, podría usarse una proporción para describir el costo de la renta de un mes en comparación con los ingresos obtenidos en un mes. También puedes usar una proporción para comparar el número de elefantes con el número total de animales en un zoológico, o la cantidad de calorías por porción en dos marcas diferentes de helado.

Las tarifas son un tipo especial de ratio utilizado para describir una relación entre diferentes unidades de medida, como velocidad, salarios o precios. Un automóvil puede describirse como viajando 60 millas por hora; un paisajista podría ganar $35 por césped cortado; el gas se puede vender a $3 por galón.

Ratios

Ratios comparan cantidades usando división. Esto significa que puede establecer una relación entre dos cantidades como una expresión de división entre esas mismas dos cantidades.

Aquí hay un ejemplo. Si tienes un plato que contiene 10 galletas de azúcar y 20 galletas con chispas de chocolate, puedes comparar las galletas usando una proporción.

La proporción de galletas de azúcar a galletas con chispas de chocolate es:

\(\ \frac{\text { sugar cookies }}{\text { chocolate chip cookies }}=\frac{10}{20}\)

La proporción de galletas con chispas de chocolate a galletas de azúcar es:

\(\ \frac{\text { chocolate chip cookies }}{\text { sugar cookies }}=\frac{20}{10}\)

Puedes escribir la relación usando palabras, una fracción, y también usando dos puntos como se muestra a continuación.

\ (\\ begin {array} {c}
\ text {ratio de} {\ color {rojo}\ texto {galletas de azúcar a}}\
\ color {azul}\ texto {galletas con chispas de chocolate}\\
{\ color {rojo} 10}\ texto {a}\ color {azul} 20\\
\ frac {\ color {rojo} 10} {\ color {azul} 20}\\
{\ color {rojo}} 10}:\ color {azul} 20
\ end {array}\)

Algunas personas piensan en esta proporción como: “Por cada 10 galletas de azúcar que tengo, tengo 20 galletas con chispas de chocolate”.

También puede simplificar la relación del mismo modo que simplifica una fracción.

\(\ \frac{10}{20}=\frac{10 \div 10}{20 \div 10}=\frac{1}{2}\)

Entonces también podemos decir que:

\ (\\ begin {array} {c}
\ text {ratio de} {\ color {rojo}\ texto {galletas de azúcar a}}\
\ color {azul}\ texto {galletas con chispas de chocolate}\\
{\ color {rojo} 1}\ texto {a}\ color {azul} 2\\
\ frac {\ color {rojo} 1} {\ color {azul} 2}\\
{\ color {rojo}} 1}:\ color {azul} 2
\ end {array}\)

Cómo escribir una relación

Una relación se puede escribir de tres maneras diferentes:

• con la palabra “a”: 3 a 4
• como una fracción:\(\ \frac{3}{4}\)
• con dos puntos: 3:4

Una relación se simplifica si es equivalente a una fracción que se ha simplificado.

A continuación se presentan dos ejemplos más que ilustran cómo comparar cantidades usando una relación, y cómo expresar la relación en forma simplificada.

Ejemplo

Un jugador de basquetbol realiza 50 tiros de salto durante una práctica. Ella hace 28 de ellos. ¿Cuál es la relación entre los disparos realizados y los disparos realizados? Simplifica la relación.

Solución

\(\ \frac{\text { shots made }}{\text { shots taken }}\)	Identificar la relación.
\(\ \frac{28}{50}\)	Exprese las dos cantidades en forma de fracción.
\(\ \frac{28 \div 2}{50 \div 2}=\frac{14}{25}\)	Simplifica la fracción para expresar la relación en la forma más simple.
\ (\\ begin {array} {r} 14:25\\ 14\ text {a} 25 \ end {array}\)	Considera las otras dos formas de escribir una relación. Si es necesario, querrás expresar tu respuesta en un formato particular.

La relación entre los disparos realizados y los disparos realizados es\(\ \frac{14}{25}\) de 14:15, o 14 a 15.

A menudo, una cantidad en la relación es mayor que la segunda cantidad. No hay que escribir la relación para que la menor cantidad sea lo primero; lo importante es mantener la relación consistente.

Ejemplo

Paul está comparando la cantidad de calorías en un gran pedido de papas fritas de sus dos restaurantes favoritos de comida rápida. Fast Foodz anuncia que un pedido de papas fritas tiene 450 calorías, y Beef Stop afirma que sus papas fritas tienen 300 calorías. Escribe una relación que represente la cantidad de calorías en las papas fritas Fast Foodz en comparación con las calorías en las papas fritas Beef Stop.

Solución

\(\ \frac{\text { calories in Fast Foodz fries }}{\text { calories in Beef Stop fries }}\)	Identificar la relación.
\(\ \frac{450}{300}\)	Escribe una relación comparando calorías.
\(\ \frac{450 \div 150}{300 \div 150}=\frac{3}{2}\)	Simplifica la relación. 450 y 300 tienen un factor común de 150.

La proporción de calorías en las papas fritas Fast Foodz a las papas fritas Beef Stop es\ frac {3} {2}, 3:2, o 3 a 2.

Las proporciones pueden comparar una parte con una parte o una parte con un todo. Considera el siguiente ejemplo que describe a los invitados a una fiesta.

Ejemplo

Luisa invita a un grupo de amigos a una fiesta. Incluyendo a Luisa, hay un total de 22 personas, 10 de las cuales son mujeres.

Cuál es mayor: ¿la proporción de mujeres a hombres en la fiesta, o la proporción de mujeres con respecto al número total de personas presentes?

Solución

\(\ \frac{\text { number of women }}{\text { number of men }}\)	Identificar la primera relación.
\(\ \frac{10}{12}\)	Escribe una proporción comparando mujeres con hombres. Ya que hay 22 personas y 10 son mujeres, 12 deben ser hombres.
\(\ \frac{10 \div 2}{12 \div 2}=\frac{5}{6}\)	Simplifica la relación. 10 y 12 tienen un factor común de 2; la proporción de mujeres a hombres en la fiesta es\(\ \frac{5}{6}\).
\(\ \frac{\text { number of women }}{\text { number of people }}\)	Identificar la siguiente relación.
\(\ \frac{10}{22}\)	Escribe una relación comparando el número de mujeres con el número total de personas en la fiesta.
\(\ \frac{10 \div 2}{22 \div 2}=\frac{5}{11}\)	Simplifica la relación. 10 y 22 tienen un factor común de 2.
\ (\\ begin {array} {l} \ frac {5\ cdot 11} {6\ cdot 11} =\ frac {55} {66}\ \ frac {5\ cdot 6} {11\ cdot 6} =\ frac {30} {66} \ end {array}\)	Reescribe cada fracción con un denominador común, 66.
\(\ \frac{5}{6}>\frac{5}{11}\)	Ya que\(\ \frac{55}{66}>\frac{30}{66}\).

La proporción de mujeres a hombres en la fiesta,\(\ \frac{5}{6}\), es mayor que la proporción de mujeres con respecto al número total de personas,\(\ \frac{5}{11}\).

Ejercicio

Una encuesta realizada en la Universidad Forrester encontró que 4 mil de 6 mil estudiantes no están casados. Encuentra la proporción de estudiantes solteros y casados. Expresar como una relación simplificada.

1. 3 a 2
2. 1 a 3
3. 2 a 1
4. 2 a 3

Contestar

1. Incorrecto. La relación 3 a 2 compara el número total de estudiantes con el número de estudiantes solteros. La respuesta correcta es 2 a 1.
2. Incorrecto. La relación 1 a 3 compara el número de estudiantes casados con el número total de estudiantes. La respuesta correcta es 2 a 1.
3. Correcto. Si 4 mil estudiantes de 6 mil son solteros, entonces dos mil deben estar casados. La proporción de estudiantes solteros a casados puede representarse como 4,000 a 2,000, o simplemente 2 a 1.
4. Incorrecto. La relación 2 a 3 compara el número de estudiantes solteros con el número total de estudiantes. La respuesta correcta es 2 a 1.

Tarifas

Una tasa es una relación que compara dos cantidades diferentes que tienen diferentes unidades de medida. Una tarifa es una comparación que proporciona información como dólares por hora, pies por segundo, millas por hora y dólares por cuarto de galón, por ejemplo. La palabra “per” suele indicar que estás tratando con una tarifa. Las tarifas se pueden escribir usando palabras, usando dos puntos, o como una fracción. Es importante que sepas qué cantidades se están comparando.

Por ejemplo, un empleador quiere rentar 6 autobuses para transportar a un grupo de 300 personas en una salida de empresa. La tasa para describir la relación se puede escribir usando palabras, usando dos puntos, o como una fracción; y debes incluir las unidades.

\ (\\ begin {array} {c}
\ text {seis autobuses por} 300\ texto {personas}\\
6\ texto {buses:} 300\ texto {personas}\
\ frac {6\ texto {autobuses}} {300\ texto {personas}}
\ end {array}\)

Al igual que con las relaciones, esta tasa se puede expresar en forma más simple simplificando la fracción.

\(\ \frac{6 \text { buses}{\div6 }}{300 \text { people}{\div6 }}=\frac{1 \text { bus }}{50 \text { people }}\)

Esta fracción significa que la tasa de autobuses a personas es de 6 a 300 o, simplificado, 1 autobús por cada 50 personas.

Ejemplo

Escribe la tarifa como fracción simplificada: 8 líneas telefónicas para 36 empleados.

Solución

\(\ \frac{8 \text { phone lines }}{36 \text { employees }}\)	Escribir como una fracción.
\(\ \frac{8 \text { phone lines}{\div4 }}{36 \text { employees}{\div4 }}=\frac{2 \text { phone lines }}{9 \text { employees }}\)	Simplifica la fracción usando el factor común de 4.

La tasa de líneas telefónicas para los empleados se puede expresar como\(\ \frac{2 \text { phone lines }}{9 \text { employees }}\).

Ejemplo

Escriba la tarifa como fracción simplificada: 6 auxiliares de vuelo para 200 pasajeros.

Solución

\(\ \frac{6 \text { flight attendants }}{200 \text { passengers }}\)	Escribir como una fracción.
\(\ \frac{6 \text { flight attendants}{\div2 }}{200 \text { passengers}\div2}=\frac{3 \text { flight attendants }}{100 \text { passengers }}\)	Simplifica la fracción usando el factor común de 2.

La tasa de asistentes de vuelo a pasajeros es\(\ \frac{3 \text { flight attendants }}{100 \text { passengers }}\).

Ejercicio

Anyla monta su bicicleta 18 cuadras en 20 minutos. Expresar su tarifa como una fracción simplificada.

1. \(\ 18: 20\)
2. \ (\\ begin {array} {cc}
   9 &\ text {bloques}\\
   \ hline 10 &\ texto {minutos}
   \ end {array}\)
3. \(\ \frac{9 \text { minutes }}{10 \text { blocks }}\)
4. \(\ \frac{18 \text { blocks }}{20 \text { minutes }}\)

Contestar

1. \(\ 18: 20\)

   Incorrecto. El viaje de Anyla compara cantidades con diferentes unidades, por lo que puede describirse como una tarifa. Dado que las tarifas comparan dos cantidades medidas en diferentes unidades de medida, deben incluir sus unidades. La respuesta correcta es\ (\\ begin {aligned}
   9 &\ text {blocks}\\
   \ hline 10 &\ text {minutes}
   \ end {aligned}\).

2. \ (\\ begin {array} {cc}
   9 &\ text {bloques}\\
   \ hline 10 &\ texto {minutos}
   \ end {array}\)

   Correcto. El viaje de Anyla compara cantidades con diferentes unidades (bloques y minutos), por lo que es una tarifa y se puede escribir\ (\\ begin {array} {cc}
   18 &\ text {blocks}\
   \\ hline 20 &\ text {minutes}
   \ end {array}\). Esta fracción se puede simplificar dividiendo tanto el numerador como el denominador por 2.

3. \(\ \frac{9 \text { minutes }}{10 \text { blocks }}\)

   Incorrecto. 18 cuadras en 20 minutos no equivale a 10 cuadras en 9 minutos. Vuelve a consultar las unidades en tu respuesta. La respuesta correcta es\ (\\ begin {aligned}
   9 &\ text {blocks}\\
   \ hline 10 &\ text {minutes}
   \ end {aligned}\).

4. \(\ \frac{18 \text { blocks }}{20 \text { minutes }}\)

   Incorrecto. El viaje de Anyla compara cantidades con diferentes unidades, por lo que puede describirse como una tarifa. Esta es una representación correcta e incluye las unidades, pero la fracción se puede simplificar. La respuesta correcta es\ (\\ begin {aligned}
   9 &\ text {blocks}\\
   \ hline 10 &\ text {minutes}
   \ end {aligned}\).

Encontrar tarifas unitarias

Una tasa unitaria compara una cantidad con una unidad de medida. A menudo se ve la velocidad a la que viaja un objeto en términos de su tarifa unitaria.

Por ejemplo, si quisieras describir la velocidad de un niño montando su bicicleta —y tuvieras la medición de la distancia que recorrió en millas en 2 horas— lo más probable es que expreses la velocidad describiendo la distancia recorrida en una hora. Esta es una tarifa unitaria; da la distancia recorrida por una hora. El denominador de una tasa unitaria siempre será uno.

Considera el ejemplo de un auto que recorre 300 millas en 5 horas. Para encontrar la tarifa unitaria, se encuentra el número de millas recorridas en una hora.

\(\ \frac{300 \text { miles}{\div5 }}{5 \text { hours}{\div5 }}=\frac{60 \text { miles }}{1 \text { hour }}\)

Una forma común de escribir esta tarifa unitaria es de 60 millas por hora.

Ejemplo

Un tren subterráneo abarrotado cuenta con 375 pasajeros distribuidos de manera uniforme entre 5 automóviles. ¿Cuál es la tarifa unitaria de pasajeros por vagón del metro?

Solución

\(\ \frac{\text { passengers }}{\text { subway cars }}\)	Identificar la relación.
\(\ \frac{375 \text { passengers }}{5 \text { subway cars }}\)	Escribe la tasa como una fracción.
\(\ \frac{375 \text { passengers } \div 5}{5 \text { subway cars } \div 5}=\frac{75 \text { passengers }}{1 \text { subway car }}\)	Exprese la fracción con 1 en el denominador para encontrar el número de pasajeros en un vagón del metro.

La tarifa unitaria del vagón del metro es de 75 pasajeros por vagón del metro.

Encontrar precios unitarios

Un precio unitario es una tasa unitaria que expresa el precio de algo. El precio unitario siempre describe el precio de una unidad, para que puedas comparar fácilmente los precios.

Es posible que hayas notado que las repisas de comestibles están marcadas con el precio unitario (así como el precio total) de cada producto. Este precio unitario facilita a los compradores comparar los precios de marcas competidoras y diferentes tamaños de paquetes.

Considera los dos contenedores de arándanos que se muestran a continuación. Puede ser difícil decidir cuál es la mejor compra con solo mirar los precios; el contenedor de la izquierda es más barato, pero también obtienes menos arándanos. Un mejor indicador de valor es el precio por onza única de arándanos por cada contenedor.

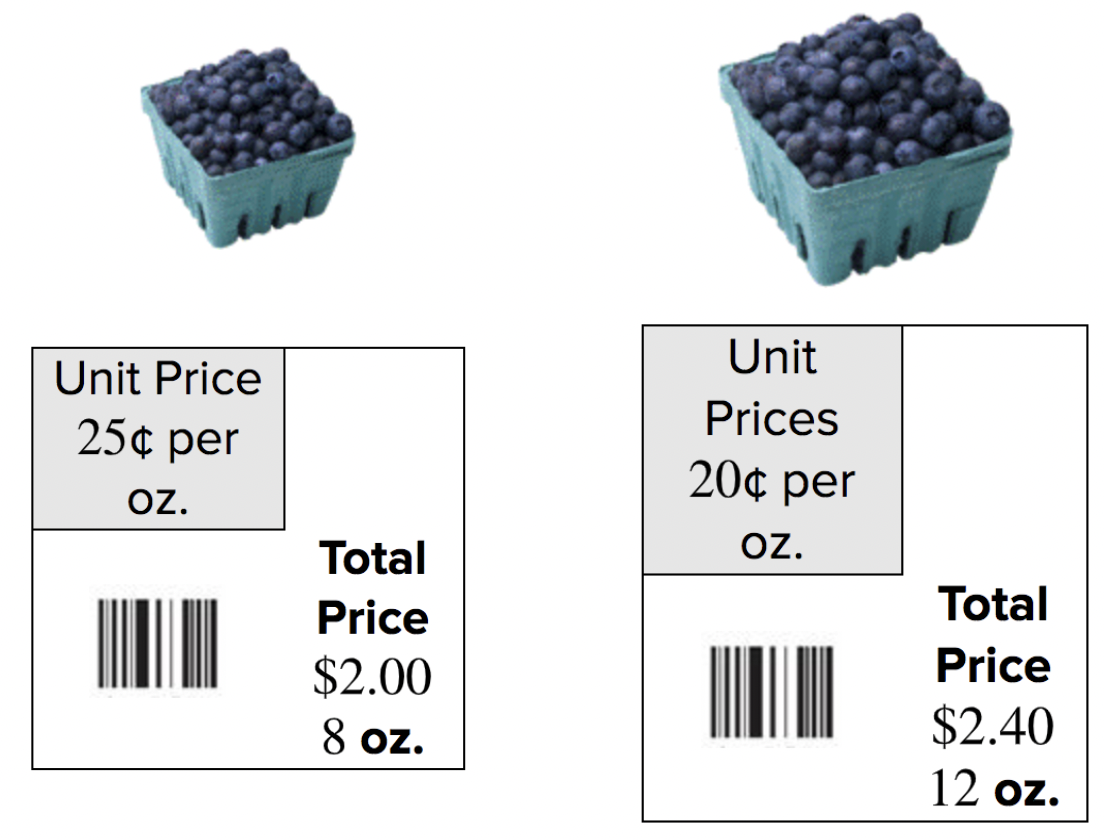
Mira los precios unitarios: el contenedor de la derecha es en realidad una mejor oferta, ya que el precio por onza es menor que el precio unitario del contenedor de la izquierda. Pagas más dinero por el contenedor más grande de arándanos, pero también obtienes más arándanos de los que lo harías con el contenedor más pequeño. En pocas palabras, el contenedor de la derecha tiene un mejor valor que el contenedor de la izquierda.

Entonces, ¿cómo encuentra el precio unitario?

Imagina que un comprador quería usar precios unitarios para comparar un paquete de 3 pañuelos por $4.98 con una sola caja de pañuelos con un precio de $1.60. ¿Cuál es el mejor trato?

Encuentra el precio unitario del paquete de 3:\(\ \frac{\$ 4.98}{3 \text { boxes }}\)

Ya que el precio dado es por 3 cajas, divide tanto el numerador como el denominador por 3 para obtener el precio de 1 caja, el precio unitario. El precio unitario es de $1.66 por caja.

El precio unitario del paquete de 3 es de $1.66 por caja; compárelo con el precio de una sola caja en $1.60. Sorprendentemente, ¡el paquete de 3 tiene un precio unitario más alto! La compra de una sola caja es el mejor valor.

Al igual que las tarifas, los precios unitarios a menudo se describen con la palabra “per.” A veces, una línea inclinada/se usa para significar “per.” El precio del pañuelo podría estar escrito $1.60/caja, que se lee “$1.60 por caja”.

Ejemplo

3 libras de puntas de solomillo cuestan $21. ¿Cuál es el precio unitario por libra?

Solución

\(\ \frac{\$ 21.00}{3 \text { pounds }}\)	Escribe una tasa para representar el costo por número de libras.
\(\ \frac{\$ 21.00 \div 3}{3 \text { pounds}{\div3 }}=\frac{\$ 7.00}{1 \text { pound }}\)	Exprese la fracción con 1 en el denominador dividiendo tanto el numerador como el denominador por 3.

El precio unitario de las puntas de solomillo es de $7.00/libra.

El siguiente ejemplo muestra cómo utilizar el precio unitario para comparar dos productos y determinar cuál tiene el precio más bajo.

Ejemplo

Sami está tratando de decidir entre dos marcas de galletas. ¿Qué marca tiene el precio unitario más bajo?

Marca A: $1.12 por 8 onzas

Marca B: $1.56 por 12 onzas

Solución

Marca A
\(\ \frac{\$ 1.12}{8 \text { ounces }}\)	Escriba una tasa para representar el costo por onza para la Marca A.
\(\ \frac{\$ 1.12 \div 8}{8 \text { ounces}{\div8 }}=\frac{\$ 0.14}{1 \text { ounce }}\)	Encuentra el precio unitario de la Marca A dividiendo tanto el numerador como el denominador por 8.
Marca B
\(\ \frac{\$ 1.56}{12 \text { ounces }}\)	Escriba una tasa para representar el costo por onza para la Marca B.
\(\ \frac{\$ 1.56 \div 12}{12 \text { ounces }{\div12 }}=\frac{\$ 0.13}{1 \text { ounce }}\)	Encuentra el precio unitario de la Marca B dividiendo tanto el numerador como el denominador por 12.
\(\ \frac{\$ 0.14}{1 \text { ounce }}>\frac{\$ 0.13}{1 \text { ounce }}\)	Compara precios unitarios.

El precio unitario de las galletas Marca A es de 14 centavos por onza y el precio unitario de la Marca B es de 13 centavos por onza. La marca B tiene un precio unitario más bajo y representa el mejor valor.

Ejercicio

Un comprador está comparando dos paquetes de arroz en la tienda de abarrotes. Un paquete de 10 libras cuesta $9.89 y un paquete de 2 libras cuesta $1.90. ¿Qué paquete tiene el precio unitario más bajo al centavo más cercano? ¿Cuál es su precio unitario?

1. La bolsa de 2 libras tiene un precio unitario menor de $.95/libra.
2. La bolsa de 10 libras tiene un precio unitario menor de $0.99/libra.
3. La bolsa de 10 libras tiene un precio unitario menor de $.95/libra.
4. La bolsa de 2 libras tiene un precio menor de $1.89/2pound.

Contestar

1. Correcto. El precio unitario por libra para la bolsa de 2 libras es\(\ \$ 1.90 \div 2=\$ 0.95\). El precio unitario por libra para la bolsa de 10 libras es\(\ \$ 9.89 \div 10=\$ 0.989\), que ronda a $0.99.
2. Incorrecto. \(\ \$ 9.89 \div 10=\$ 0.989\), que redondea a $0.99. \(\ \$ 1.90 \div 2=\$ 0.95\). La bolsa de 2 libras tiene un precio unitario menor. La respuesta correcta es A.
3. Incorrecto. \(\ \$ 9.89 \div 10=\$ 0.989\), que redondea a $0.99. La respuesta correcta es A.
4. Incorrecto. Un precio unitario es el precio de una unidad; en este caso, es necesario encontrar el costo de una libra, no de dos libras. La respuesta correcta es A.

Resumen

Las proporciones y tasas se utilizan para comparar cantidades y expresar relaciones entre cantidades medidas en las mismas unidades de medida y en diferentes unidades de medida. Ambos pueden escribirse como una fracción, usando dos puntos, o usando las palabras “a” o “por”. Dado que las tarifas comparan dos cantidades medidas en diferentes unidades de medida, como dólares por hora o días de enfermedad al año, deben incluir sus unidades. Una tasa unitaria o precio unitario es una tasa que describe la tasa o precio de una unidad de medida.