6.2.3: Uso de conversiones métricas para resolver problemas

Última actualización
Guardar como PDF

Page ID: 111488

The NROC Project

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

Resuelva problemas de aplicación que involucran unidades métricas de longitud, masa y volumen.

Introducción

Aprender a resolver problemas del mundo real usando conversiones métricas es tan importante como aprender a hacer las conversiones ellos mismos. Matemáticos, científicos, enfermeras e incluso atletas a menudo se enfrentan a situaciones en las que se les presenta información usando mediciones métricas, y luego deben tomar decisiones informadas basadas en esos datos.

Para resolver estos problemas de manera efectiva, es necesario comprender el contexto de un problema, realizar conversiones y luego verificar la razonabilidad de su respuesta. Realice estos tres pasos y tendrá éxito en cualquier sistema de medición que se encuentre utilizando.

Comprender el contexto y realizar conversiones

El primer paso para resolver cualquier problema del mundo real es entender su contexto. Esto te ayudará a descubrir qué tipo de soluciones son razonables (y el problema en sí puede darte pistas sobre qué tipos de conversiones son necesarias). Aquí hay un ejemplo.

Ejemplo

En los Juegos Olímpicos de Verano, los atletas compiten en carreras de las siguientes longitudes: 100 metros, 200 metros, 400 metros, 800 metros, 1500 metros, 5000 metros y 10,000 metros. Si un corredor corriera en todas estas carreras, ¿cuántos kilómetros correría?

Solución

\ (\\ begin {array} {r}
10,000\\
5,000\
1,500\\
800\\
400\\
200\
+\ quad 100\\
\ hline 18,000
\ end {array}\)

Para averiguar cuántos kilómetros correría, primero hay que sumar todas las longitudes de las carreras juntas y luego convertir esa medida en kilómetros.

$\ \frac{18,000 \text { meters }}{1} \cdot \frac{1 \text { kilometer }}{1,000 \text { meters }}=? \text { kilometers }$

Utilice el método de etiqueta factorial y las fracciones unitarias para convertir de metros a kilómetros.

$\ \frac{18,000\cancel{\mathrm{~m}}}{1} \cdot \frac{1 \mathrm{~km}}{1,000 \cancel{\mathrm{~m}}}=? \mathrm{~km}$

$\ \frac{18,000}{1} \cdot \frac{1 \text { kilometer }}{1,000}=\frac{18,000 \text { kilometers }}{1,000}$

$\ \frac{18,000 \text { kilometers }}{1,000}=18 \text { kilometers }$

Cancelar, multiplicar y resolver.

El corredor correría 18 kilómetros.

Puede que esto no sea probable que suceda (un corredor tendría que ser todo un atleta para competir en todas estas carreras) pero es una pregunta interesante a considerar. El problema requería que encontraras la distancia total que recorrería el corredor (en kilómetros). El ejemplo mostró cómo sumar las distancias, en metros, para luego convertir ese número a kilómetros.

A continuación se muestra un ejemplo con un contexto diferente, pero que aún requiere conversiones.

Ejemplo

Una botella contiene 295 decilitros mientras que otra contiene 28,000 mililitros. ¿Cuál es la diferencia de capacidad entre las dos botellas?

Solución

\ (\\ begin {array} {r} 295\ texto {decilitros} =\ texto {? litros}\\ 28,000\ text {mililitros} =? \ text {litros} \ end {array}\)	Las dos medidas están en diferentes unidades. Puede convertir ambas unidades a litros y luego compararlas.
$\ \frac{295 \text { deciliters }}{1} \cdot \frac{1 \text { liter }}{10 \text { deciliters }}=? \text { liters }$	Convertir decilitros en litros.
$\ \frac{295 \mathrm{~dl}}{1} \cdot \frac{1 \mathrm{~L}}{10 \mathrm{~dl}}=? \mathrm{~L}$	Cancelar unidades similares y multiplicar.
\ (\\ begin {array} {r} \ frac {295} {1}\ cdot\ frac {1\ text {litro}} {10} =\ frac {295\ texto {litros}} {10}\ \ frac {295\ texto {litros}} {10} =29.5\ texto {litros} \ end {array}\)	$\ 295 \text { deciliters }=29.5 \text { liters }$
$\ \frac{28,000 \text { milliliters }}{1} \cdot \frac{1 \text { liter }}{1,000 \text { milliliters }}=? \text { liters }$	Convertir mililitros en litros.
$\ \frac{28,000 \cancel{\text { ml }}}{1} \cdot \frac{1 \mathrm{~L}}{1,000 \cancel{\mathrm{~ml}}}=? \mathrm{~L}$ $\ \frac{28,000}{1} \cdot \frac{1 \text { liter }}{1,000}=\frac{28,000 \text { liters }}{1,000}$ $\ \frac{28,000 \text { liters }}{1,000}=28 \text { liters }$	$\ 28,000 \text { milliliters }=28 \text { liters }$
$\ 29.5 \text { liters }-28 \text { liters }=1.5 \text { liters }$	La pregunta pregunta por “diferencia de capacidad” entre las botellas.

Hay una diferencia de capacidad de 1.5 litros entre las dos botellas.

Este problema pedía la diferencia entre dos cantidades. La forma más fácil de encontrar esto es convertir una cantidad para que ambas cantidades se midan en la misma unidad, y luego restar una de la otra.

Ejercicio

Un boxeador pesa 85 kilogramos. Es 80 dekagramas más pesado que su oponente. ¿Cuánto pesa su oponente?

$\ 5 \text { kilograms }$
$\ 84.2 \text { kilograms }$
$\ 84.92 \text { kilograms }$
$\ 85.8 \text { kilograms }$

Responder

Incorrecto. Mira las etiquetas de las unidades. El boxeador es 80 dekagramas más pesado, no 80 kilogramos más pesado. La respuesta correcta es de 84.2 kilogramos.
Correcto. $\ 80 \text { dekagrams }=0.8 \text { kilograms }$, y$\ 85-0.8=84.2$.
Incorrecto. Esto hubiera sido cierto si la diferencia de peso fuera de 8 dekagramas, no 80 dekagramas. La respuesta correcta es de 84.2 kilogramos.
Incorrecto. El primer boxeador es 80 dekagramas más pesado, no más ligero que su oponente. Esta pregunta pregunta por el peso del oponente. La respuesta correcta es de 84.2 kilogramos.

Comprobando tus conversiones

A veces es una buena idea verificar tus conversiones usando un segundo método. Esto generalmente te ayuda a detectar cualquier error que puedas cometer, como usar las fracciones unitarias incorrectas o mover el punto decimal de manera incorrecta.

Ejemplo

Una botella de dos litros contiene 87 centilitros de aceite y 4.1 decilitros de agua. ¿Cuánto más líquido se necesita para llenar la botella?

Solución

$\ 87 \text { centiliters }+4.1 \text { deciliters }+?=2 \text { liters }$	Estás buscando la cantidad de líquido necesario para llenar la botella. Convierte ambas medidas a litros y luego resuelve el problema.
$\ 87 \text { centiliters }=\text { ? liters }$ $\ \frac{87 \text { centiliters }}{1} \cdot \frac{1 \text { liters }}{100 \text { centiliters }}=? \text { liters }$ $\ \frac{87 \cancel{\mathrm { cl }}}{1} \cdot \frac{1 \mathrm{~L}}{100 \cancel{\mathrm{~cl}}}=? \mathrm{~L}$ $\ \frac{87}{1} \cdot \frac{1 \text { liter }}{100}=\frac{87 \text { liters }}{100}$ $\ \frac{87 \text { liters }}{100}=0.87 \text { liters }$	Convierte 87 centilitros en litros.
$\ \text { 4.1 deciliters }=\text { ? liters }$ $\ \frac{4.1 \text { deciliters }}{1} \cdot \frac{1 \text { liter }}{10 \text { deciliters }}=? \text { liters }$ $\ \frac{4.1 \cancel{\mathrm{~dl}}}{1} \cdot \frac{1 \mathrm{~L}}{10 \cancel{\mathrm{~dl}}}=? \mathrm{~L}$ $\ \frac{4.1}{1} \cdot \frac{1 \text { liter }}{10}=\frac{4.1 \text { liters }}{10}$ $\ \frac{4.1 \text { liters }}{10}=0.41 \text { liters }$	Convierte 4.1 decilitros en litros.
$\ 87 \text { centiliters }+4.1 \text { deciliters }+?=2 \text { liters }$ $\ 0.87 \text { liter }+0.41 \text { liter }+?=2 \text { liters }$ $\ 2 \text { liters }-0.87 \text { liter }-0.41 \text { liter }=0.72 \text { liter }$	Restar para encontrar cuánto más líquido se necesita para llenar la botella.

La cantidad de líquido necesario para llenar la botella es de 0.72 litros.

Una vez que se te ocurra la respuesta, también podrías verificar tus conversiones usando el método más rápido de “mover el decimal”, que se muestra a continuación.

Ejemplo

Una botella de dos litros contiene 87 centilitros de aceite y 4.1 decilitros de agua. ¿Cuánto más líquido se necesita para llenar la botella?

Solución

$\ 87 \text { centiliters }+4.1 \text { deciliters }+?=2 \text { liters }$	Estás buscando la cantidad de líquido necesario para llenar la botella.
$\ 87 \text { centiliters }=\text { ? liters }$	Convierte 87 centilitros en litros.
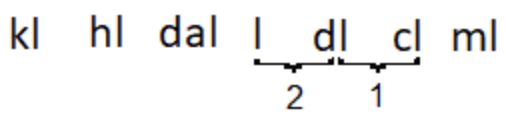$Screen Shot 2021-05-04 at 1.19.58 PM.png$	En la tabla, los litros (l) son dos lugares a la izquierda de los centilitros (cl).
$Screen Shot 2021-05-04 at 1.22.02 PM.png$ $\ 87 \text { centiliters }=0.87 \text { liters }$	Mueve el punto decimal dos lugares a la izquierda en 87 centilitros.
$\ \text { 4.1 deciliters }=\text { ? liters }$	Convierte 4.1 decilitros en litros.
$Screen Shot 2021-05-04 at 1.25.01 PM.png$	En la tabla, litro (l) es un lugar a la izquierda del decilitro (dl).
$\ \text { 4.1 } \text { deciliters }=0.41 \text { liters }$	Mueve el punto decimal un lugar a la izquierda en 4.1 decilitros.
$\ 87 \text { centiliters }+4.1 \text { deciliters }+?=2 \text { liters }$ $\ 0.87 \text { liter }+0.41 \text { liter }+?=2 \text { liters }$ $\ 2 \text { liters }-0.87 \text { liter }-0.41 \text { liter }=0.72 \text { liter }$	Restar para encontrar cuánto más líquido se necesita para llenar la botella.

La cantidad de líquido necesario para llenar la botella es de 0.72 litros.

La respuesta inicial comprueba. Se necesita 0.72 litros de líquido para llenar la botella. Verificar una conversión con otro método es una buena práctica para detectar cualquier error en la escala.

Resumen

Comprender el contexto de los problemas de aplicación de la vida real es importante. Busque palabras dentro del problema que le ayuden a identificar qué operaciones se necesitan, y luego aplicar las conversiones de unidades correctas. Verificar su respuesta final usando otro método de conversión (como el método “mover el decimal”, si ha utilizado el método de etiqueta de factor para resolver el problema) puede reducir los errores en sus cálculos.

\ (\\ begin {array} {r} 295\ texto {decilitros} =\ texto {? litros}\\ 28,000\ text {mililitros} =? \ text {litros} \ end {array}\)	Las dos medidas están en diferentes unidades. Puede convertir ambas unidades a litros y luego compararlas.
\(\ \frac{295 \text { deciliters }}{1} \cdot \frac{1 \text { liter }}{10 \text { deciliters }}=? \text { liters }\)	Convertir decilitros en litros.
\(\ \frac{295 \mathrm{~dl}}{1} \cdot \frac{1 \mathrm{~L}}{10 \mathrm{~dl}}=? \mathrm{~L}\)	Cancelar unidades similares y multiplicar.
\ (\\ begin {array} {r} \ frac {295} {1}\ cdot\ frac {1\ text {litro}} {10} =\ frac {295\ texto {litros}} {10}\ \ frac {295\ texto {litros}} {10} =29.5\ texto {litros} \ end {array}\)	\(\ 295 \text { deciliters }=29.5 \text { liters }\)
\(\ \frac{28,000 \text { milliliters }}{1} \cdot \frac{1 \text { liter }}{1,000 \text { milliliters }}=? \text { liters }\)	Convertir mililitros en litros.
\(\ \frac{28,000 \cancel{\text { ml }}}{1} \cdot \frac{1 \mathrm{~L}}{1,000 \cancel{\mathrm{~ml}}}=? \mathrm{~L}\) \(\ \frac{28,000}{1} \cdot \frac{1 \text { liter }}{1,000}=\frac{28,000 \text { liters }}{1,000}\) \(\ \frac{28,000 \text { liters }}{1,000}=28 \text { liters }\)	\(\ 28,000 \text { milliliters }=28 \text { liters }\)
\(\ 29.5 \text { liters }-28 \text { liters }=1.5 \text { liters }\)	La pregunta pregunta por “diferencia de capacidad” entre las botellas.

\(\ 87 \text { centiliters }+4.1 \text { deciliters }+?=2 \text { liters }\)	Estás buscando la cantidad de líquido necesario para llenar la botella. Convierte ambas medidas a litros y luego resuelve el problema.
\(\ 87 \text { centiliters }=\text { ? liters }\) \(\ \frac{87 \text { centiliters }}{1} \cdot \frac{1 \text { liters }}{100 \text { centiliters }}=? \text { liters }\) \(\ \frac{87 \cancel{\mathrm { cl }}}{1} \cdot \frac{1 \mathrm{~L}}{100 \cancel{\mathrm{~cl}}}=? \mathrm{~L}\) \(\ \frac{87}{1} \cdot \frac{1 \text { liter }}{100}=\frac{87 \text { liters }}{100}\) \(\ \frac{87 \text { liters }}{100}=0.87 \text { liters }\)	Convierte 87 centilitros en litros.
\(\ \text { 4.1 deciliters }=\text { ? liters }\) \(\ \frac{4.1 \text { deciliters }}{1} \cdot \frac{1 \text { liter }}{10 \text { deciliters }}=? \text { liters }\) \(\ \frac{4.1 \cancel{\mathrm{~dl}}}{1} \cdot \frac{1 \mathrm{~L}}{10 \cancel{\mathrm{~dl}}}=? \mathrm{~L}\) \(\ \frac{4.1}{1} \cdot \frac{1 \text { liter }}{10}=\frac{4.1 \text { liters }}{10}\) \(\ \frac{4.1 \text { liters }}{10}=0.41 \text { liters }\)	Convierte 4.1 decilitros en litros.
\(\ 87 \text { centiliters }+4.1 \text { deciliters }+?=2 \text { liters }\) \(\ 0.87 \text { liter }+0.41 \text { liter }+?=2 \text { liters }\) \(\ 2 \text { liters }-0.87 \text { liter }-0.41 \text { liter }=0.72 \text { liter }\)	Restar para encontrar cuánto más líquido se necesita para llenar la botella.