6.2.2: Conversión dentro del Sistema Métrico
- Page ID
- 111482
- Realizar cálculos aritméticos en unidades métricas de longitud, masa y volumen.
Introducción
Si bien es importante conocer las diferentes unidades utilizadas en el sistema métrico, el propósito real detrás del aprendizaje del sistema métrico es que puedas usar estas unidades de medida para calcular el tamaño, la masa o el volumen de diferentes objetos. En la práctica, a menudo es necesario convertir una medida métrica en otra unidad. Esto ocurre con frecuencia en los campos médico, científico y técnico, donde el sistema métrico es comúnmente utilizado.
Si tiene una receta para 5,000 miligramos de medicamento, y al llenarlo, la dosis dice 5 gramos de medicamento, ¿cometió un error el farmacéutico?
Por un momento, imagina que eres farmacéutico. Recibes tres recetas de amoxicilina líquida: una requiere 2.5 centilitros, otra para 0.3 decilitros y otra para 450 mililitros. La amoxicilina se almacena en el refrigerador en recipientes de 1 litro, 1 decilitro y 1 centilitro. ¿Qué recipiente debe usar para asegurarse de que no está desperdiciando nada del medicamento no utilizado?
Para resolver este problema, necesitas saber cómo convertir de una medida a otra así como cómo sumar diferentes cantidades juntas. Echemos un vistazo a cómo hacer esto.
Conversión de unidades más grandes a unidades más pequeñas
Convertir entre medidas en el sistema métrico es simplemente una cuestión de identificar la unidad que tiene, la unidad a la que desea convertir, y luego contar el número de unidades entre ellas. A continuación se muestra un ejemplo básico de esto.
Convierte 1 kilómetro en decímetros.
Solución
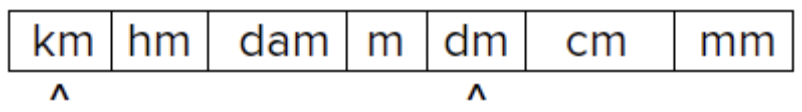 |
Identificar ubicaciones de kilómetros y decímetros. Los kilómetros (km) son mayores que decímetros (dm), por lo que se espera que haya más de un dm en un km. |
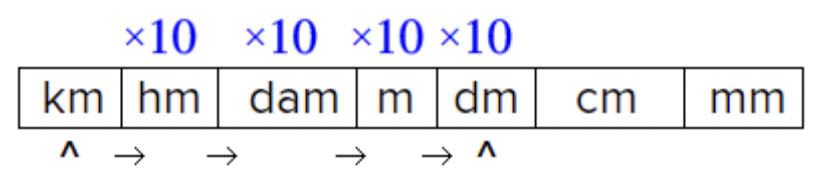 |
Contar las unidades intermedias, multiplicando por 10 a medida que avanza. |
| \(\ 1 \text { kilometer } \cdot 10 \cdot 10 \cdot 10 \cdot 10=10,000 \text { decimeters }\) |
(Ya que vas de una unidad más grande a una unidad más pequeña, multiplicas.) Multiplicar para encontrar el número de decímetros en un kilómetro. |
\(\ 1 \text { kilometer }=10,000 \text { decimeters }\)
Este problema es sencillo porque estás convirtiendo 1 kilómetro a otra unidad. El siguiente ejemplo muestra cómo resolverías este problema si te pidieran convertir 8.2 kilómetros a decímetros. Observe que la mayoría de los pasos son iguales; la diferencia crítica es que se multiplica por 8.2 en el paso final.
Convertir 8.2 kilómetros a decímetros.
Solución
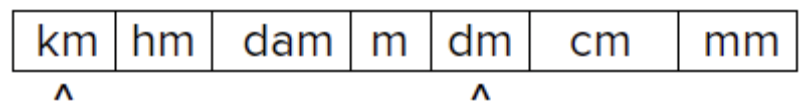 |
Identificar ubicaciones de kilómetros y decímetros. Los kilómetros (km) son mayores que decímetros (dm), por lo que se espera que haya más de un dm en un km. |
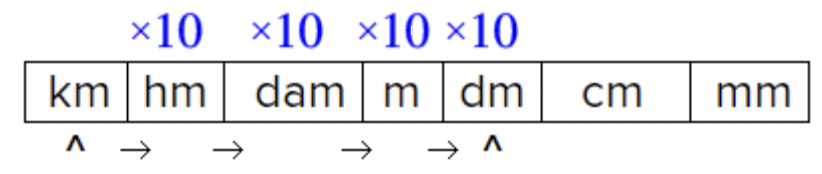 |
Contar las unidades intermedias, multiplicando por 10 a medida que avanza. |
| \(\ 8.2 \text { kilometers } \cdot 10 \cdot 10 \cdot 10 \cdot 10=82,000 \text { decimeters }\) |
Ya que vas de una unidad más grande a una unidad más pequeña, multiplica. Multiplica para encontrar el número de decímetros en 8.2 kilómetros. |
\(\ 8.2 \text { kilometers }=82,000 \text { decimeters }\)
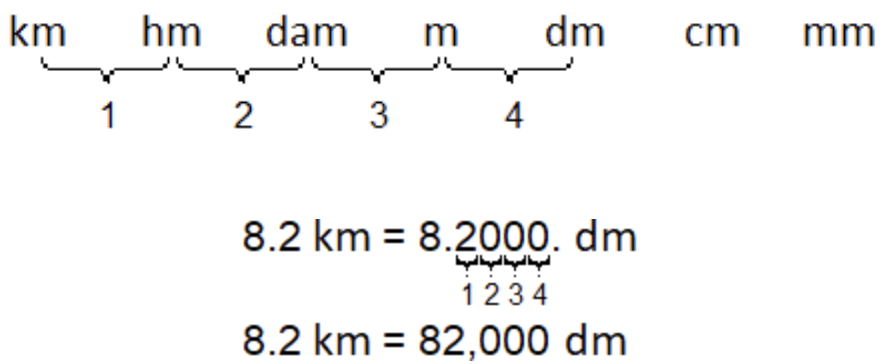
También puedes aplicar las reglas de base 10 para usar el método de acceso directo “mover el decimal” en este ejemplo. Observe cómo decímetros (dm) es cuatro lugares a la derecha de kilómetros (km); de manera similar, mueve el punto decimal cuatro lugares a la derecha al convertir 8.2 kilómetros en decímetros.
Convierte 0.55 litros en centilitros.
Solución
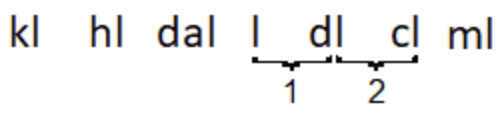 |
Contar dos lugares de litros a centilitros. |
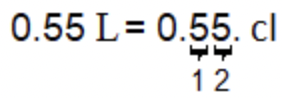 |
En 0.55 litros, mueva el punto decimal dos lugares hacia la derecha. |
\(\ 0.55 \text { liters }=55 \text { centiliters }\)
¿Cuántos dekaliters hay en 0.5 decilitros?
- 500
- 5
- 0.5
- 0.005
- Contestar
-
- Incorrecto. Un dekaliter es mayor que un decilitro, por lo que se esperaría que el número de dekaliters en 0.5 decilitros sea menor que 0.5. La respuesta correcta es 0.005.
- Incorrecto. Un dekaliter es mayor que un decilitro, por lo que se esperaría que el número de dekaliters en 0.5 decilitros sea menor que 0.5. La respuesta correcta es 0.005.
- Incorrecto. Los decilitros y dekaliters son diferentes unidades de medida, por lo que no esperaría que 0.5 decilitros equivalgan a 0.5 dekaliters. La respuesta correcta es 0.005.
- Correcto. Un decilitro es 100 veces más pequeño que un dekaliter, por lo que mueve el punto decimal dos lugares a la izquierda para convertir 0.5 decilitros a 0.005 dekaliters.
Conversión de unidades más pequeñas a más grandes
Puede utilizar procesos similares al convertir unidades más pequeñas a más grandes. Al convertir una unidad más grande en una más pequeña, se multiplica; cuando convierte una unidad más pequeña en una más grande, se divide. Aquí hay un ejemplo.
Convierte 739 centigramos en gramos.
Solución
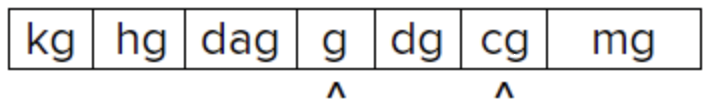 |
Identificar ubicaciones de centigramos y gramos. Los centigramas (cg) son menores que los gramos (g), por lo que se espera que haya menos de 739 gramos en 739 centigramos. |
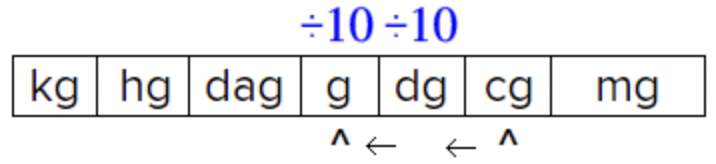 |
Contar las unidades intermedias, dividiendo por 10 a medida que avanza. |
| \(\ 739 \div 10 \div 10=7.39 \text { grams }\) |
Ya que vas de una unidad más pequeña a una unidad más grande, divide. Divide para encontrar el número de gramos en 739 centigramos. |
\(\ 739 \text { centigrams }=7.39 \text { grams }\)
Observe que el método de atajo de contar prefijos y mover el decimal el mismo número de lugares también funciona aquí. Solo asegúrate de que estás moviendo el punto decimal en la dirección correcta para la conversión.
Convierte 205.5 mililitros en kilolitros.
Solución
 |
Contar seis lugares desde mililitros hasta kilolitros. |
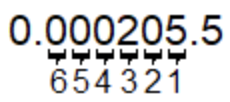 |
Los mililitros son más pequeños que los kilolitros, por lo que espera que el número 205.5 se haga más pequeño a medida que avanza en la tabla métrica. |
| \(\ 205.5 \text { milliliters }=0.0002055 \text { kiloliters }\) | En 205.5 mililitros, mueva el punto decimal seis lugares hacia la izquierda. |
\(\ 205.5 \text { milliliters }=0.0002055 \text { kiloliters }\)
Convierte 3,085 miligramos en gramos.
- \(\ 3,085,000 \text { grams }\)
- \(\ 308.5 \text { grams }\)
- \(\ 3.085 \text { grams }\)
- \(\ 0.3085 \text { grams }\)
- Contestar
-
- Incorrecto. Los gramos son más grandes que los miligramos, por lo que se esperaría que el número de gramos en 3,085 miligramos sea inferior a 3,085. La respuesta correcta es de 3,085 gramos.
- Incorrecto. Un gramo es más de 10 veces mayor que un miligramo, por lo que se esperaría que el número de gramos sea inferior a 308.5. La respuesta correcta es de 3,085 gramos.
- Correcto. Un gramo es 1,000 veces mayor que un miligramo, por lo que puedes mover el punto decimal en 3,085 tres lugares a la izquierda.
- Incorrecto. Esto es demasiado pequeño; un gramo es 1,000, no 10,000, veces más grande que un miligramo. La respuesta correcta es de 3,085 gramos.
Método de etiqueta de factor
Hay otro método que puede usar para convertir mediciones métricas: el método de etiqueta de factor. Utilizó este método cuando estaba convirtiendo unidades de medida dentro del sistema habitual de Estados Unidos.
El método de etiqueta factorial funciona igual en el sistema métrico; se basa en el uso de fracciones unitarias y la cancelación de unidades intermedias. La siguiente tabla muestra algunos de los equivalentes unitarios y fracciones unitarias para la longitud en el sistema métrico. (Debe notar que todas las fracciones unitarias contienen un factor de 10. Recuerde que el sistema métrico se basa en la noción de que cada unidad es 10 veces mayor que la que vino antes de ella.)
Además, observe que aquí se han agregado dos nuevos prefijos: mega- (que es muy grande) y micro- (que es muy pequeño).
| Equivalentes de Unidad | Factores de conversión | |
| \(\ 1 \text { meter }=1,000,000 \text { micrometers }\) | \(\ \frac{1 \mathrm{~m}}{1,000,000 \mu \mathrm{m}}\) | \(\ \frac{1,000,000 \mu \mathrm{m}}{1 \mathrm{~m}}\) |
| \(\ 1 \text { meter }=1,000 \text { millimeters }\) | \(\ \frac{1 \mathrm{~m}}{1,000 \mathrm{~mm}}\) | \(\ \frac{1,000 \mathrm{~mm}}{1 \mathrm{~m}}\) |
| \(\ 1 \text { meter }=100 \text { centimeters }\) | \(\ \frac{1 \mathrm{~m}}{100 \mathrm{~cm}}\) | \(\ \frac{100 \mathrm{~cm}}{1 \mathrm{~m}}\) |
| \(\ 1 \text { meter }=10 \text { decimeters }\) | \ (\\ begin {array} {rl} 1 &\ mathrm {~m}\\ \ hline 10 &\ mathrm {dm} \ end {array}\) |
\(\ \frac{10 \mathrm{~dm}}{1 \mathrm{~m}}\) |
| \(\ 1 \text { dekameter }=10 \text { meters }\) | \(\ \frac{1 \text { dam }}{10 \mathrm{~m}}\) | \(\ \frac{10 \mathrm{~m}}{1 \text { dam }}\) |
| \(\ 1 \text { hectometer }=100 \text { meters }\) | \(\ \frac{1 \mathrm{~hm}}{100 \mathrm{~m}}\) | \(\ \frac{100 \mathrm{~m}}{1 \mathrm{~hm}}\) |
| \(\ 1 \text { kilometer }=1,000 \text { meters }\) | \(\ \frac{1 \mathrm{~km}}{1,000 \mathrm{~m}}\) | \(\ \frac{1,000 \mathrm{~m}}{1 \mathrm{~km}}\) |
| \(\ 1 \text { megameter }=1,000,000 \text { meters }\) | \(\ \frac{1 \mathrm{~Mm}}{1,000,000 \mathrm{~m}}\) | \(\ \frac{1,000,000 \mathrm{~m}}{1 \mathrm{Mm}}\) |
Cuando aplique el método de etiqueta factorial en el sistema métrico, ¡asegúrese de verificar que no está omitiendo ninguna unidad intermedia de medida!
Convierte 7,225 centímetros en metros.
Solución
| \(\ 7,225 \text { centimeters }=? \text { meters }\) | Los metros son más grandes que centímetros, por lo que espera que su respuesta sea inferior a 7,225. |
| \(\ \frac{7,225 \text { centimeters }}{1} \cdot \frac{1 \text { meter }}{100 \text { centimeters }}=? \text { meters }\) | Usando el método de etiqueta factorial, escribe 7,225 centímetros como fracción y usa fracciones unitarias para convertirla a metros. |
|
\(\ \frac{7,225 . \cancel{\mathrm{cm}}}{1} \cdot \frac{1 \mathrm{~m}}{100 \cancel{\mathrm{~cm}}}=? \mathrm{~m}\) \(\ \frac{7,225}{1} \cdot \frac{1 \text { meter }}{100}=\frac{7,225 \text { meters }}{100}\) \(\ \frac{7,225 \text { meters }}{100}=72.25 \text { meters }\) |
Cancele unidades similares, multiplique y simplifique. |
\(\ \text { 7, } 225 \text { centimeters }=72.25 \text { meters }\)
Usando el método que prefieras, convierte 32.5 kilómetros en metros.
- \(\ 32,500 \text { meters }\)
- \(\ 325 \text { meters }\)
- \(\ 0.325 \text { meters }\)
- \(\ 0.00325 \text { meters }\)
- Contestar
-
- Correcto. Para encontrar el número de metros en 32.5 kilómetros, se puede configurar la siguiente ecuación:\(\ \frac{32.5 \text { kilometers }}{1} \cdot \frac{1,000 \text { meters }}{1 \text { kilometer }}=\frac{32,500 \text { meters }}{1}\). Las unidades de kilómetros cancelan, dejando la respuesta en metros.
- Incorrecto. Un kilómetro es más de 10 veces el tamaño de un metro; mira las fracciones unitarias y vuelve a probar tus cálculos. La respuesta correcta es de 32,500 metros.
- Incorrecto. Un kilómetro es mayor que un metro, por lo que se esperaría que el número de metros en 32.5 kilómetros sea más de 32.5. Mira las fracciones unitarias y vuelve a probar tus cálculos. La respuesta correcta es de 32,500 metros.
- Incorrecto. Un kilómetro es mayor que un metro, por lo que se esperaría que el número de metros en 32.5 kilómetros sea más de 32.5. Mira las fracciones unitarias y vuelve a probar tus cálculos. La respuesta correcta es de 32,500 metros.
Ahora que ya has visto cómo convertir entre mediciones métricas de múltiples maneras, volvamos a revisar el problema planteado anteriormente.
Si tiene una receta para 5,000 miligramos de medicamento, y al llenarlo, la dosis dice 5 gramos de medicamento, ¿cometió un error el farmacéutico?
Solución
| \(\ 5,000 \text { milligrams }=? \text { grams }\) | Necesidad de convertir miligramos a gramos. |
| \(\ \frac{5,000 \text { milligrams }}{1} \cdot \frac{1 \text { gram }}{1,000 \text { milligrams }}=? \text { grams }\) | |
|
\(\ \frac{5,000\cancel{\mathrm{~mg}}}{1} \cdot \frac{1 \mathrm{~g}}{1,000 \cancel{\mathrm{~mg}}}=? \mathrm{~g}\) \(\ \frac{5,000 \cdot 1 \text { gram }}{1 \cdot 1,000}=\frac{5,000 \text { grams }}{1,000}\) \(\ \frac{5,000 \text { grams }}{1,000}=5 \text { grams }\) |
\(\ 5 \text { grams }=5,000 \text { milligrams }\), por lo que el farmacéutico no cometió ningún error.
Resumen
Para convertir entre unidades en el sistema métrico, identifique la unidad que tiene, la unidad a la que desea convertir, y luego cuente el número de unidades entre ellas. Si vas de una unidad más grande a una unidad más pequeña, multiplica por 10 sucesivamente. Si vas de una unidad más pequeña a una unidad más grande, divides por 10 sucesivamente. El método de etiqueta factorial también se puede aplicar a las conversiones dentro del sistema métrico. Para utilizar el método de etiqueta factorial, se multiplica la medida original por fracciones unitarias; esto le permite representar la medida original en una unidad de medida diferente.


