8.1.1: Graficar datos
- Page ID
- 111403
- Leer e interpretar datos de tablas y pictogramas.
- Leer e interpretar datos de gráficos de barras e histogramas.
Introducción
Una enfermera está recolectando datos del tipo de sangre de sus pacientes. Cuando se registra a un nuevo paciente, la enfermera hace una simple prueba de pinchazo en el dedo para ver si la sangre del paciente es de tipo A, B, AB u O. (Estos son los cuatro posibles tipos de sangre. Cada uno también lleva un + o - para representar el factor RH, pero para nuestros propósitos, solo vamos a rastrear el tipo, no el + o -.) Realiza un seguimiento de sus resultados mediante la creación de una tabla de dos columnas con el nombre y el tipo de sangre del paciente.
| Nombre | Tipo de sangre |
| Dominique | A |
| Ilya | O |
| Raúl | AB |
| Madison | O |
| Philip | AB |
| Samuel | B |
| Josefine | O |
| Brett | O |
| Paula | B |
| Leticia | AB |
La información en esta tabla es un ejemplo de datos, o información. En este caso, la enfermera ha recabado una buena cantidad de datos sobre los tipos sanguíneos de sus pacientes. Al analizar los datos, puede conocer más sobre el rango de pacientes a los que atiende.
Los datos nos ayudan a tomar muchas clases de decisiones. Organizar los datos en gráficos puede ayudarnos a obtener una imagen clara de una situación y, a menudo, puede ayudarnos a tomar decisiones basadas en la imagen. Entonces, ¿cómo se toman los datos y se hace una foto de ellos? Echemos un vistazo.
Imágenes de Data
Volvamos al conjunto de datos utilizado anteriormente. Si la enfermera quisiera representar los datos visualmente, podría usar una pictografía. Los pictogramas representan datos usando imágenes. Esta presentación visual ayuda a ilustrar que para los datos de su tabla, la sangre Tipo O es la más común y la sangre Tipo A es la menos común.
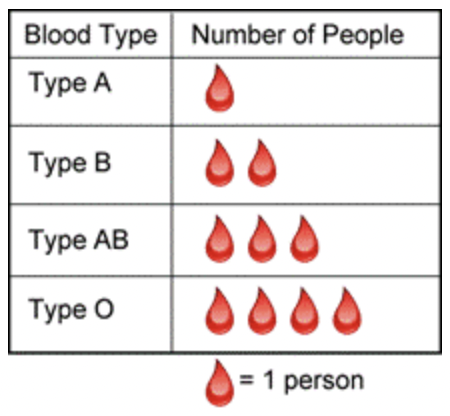
Interesada por los resultados de esta pequeña encuesta, la enfermera continúa documentando los tipos de sangre de sus pacientes hasta haber encuestado a 100 personas. Ella pone todos estos datos en una tabla, pero encuentra que es difícil para ella identificar rápidamente lo que le están diciendo los datos. Ella decide hacer otra pictografía usando una escala diferente.
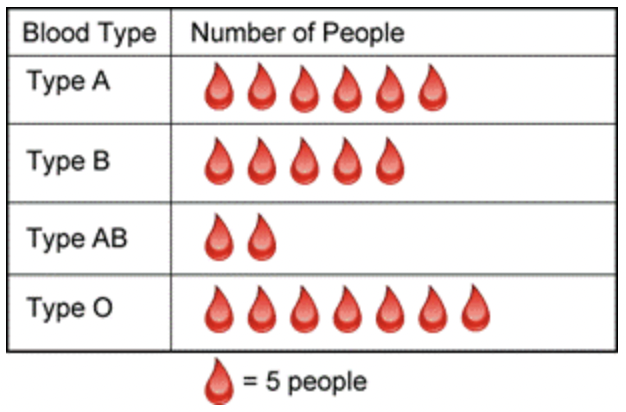
Para leer esta pictografía, todo lo que necesitas es la escala, que, en este caso, es el número de personas que representa cada símbolo de gota de sangre. En esta gráfica, cada gota de sangre representa a 5 personas. Hay seis gotas junto al Tipo A, por lo que\(\ 5 \cdot 6=30\) las personas tenían sangre Tipo A. La siguiente tabla muestra el resto de la información.
| Tipo de sangre | Número de personas |
| Tipo A | \(\ 6 \text { drops } \cdot 5 \text { people }=30 \text { people }\) |
| Tipo B | \(\ 5 \text { drops } \cdot 5 \text { people }=25 \text { people }\) |
| Tipo AB | \(\ 2 \text { drops } \cdot 5 \text { people }=10 \text { people }\) |
| Tipo O | \(\ 7 \text { drops } \cdot 5 \text { people }=35 \text { people }\) |
La pictografía a continuación muestra el número de medallas obtenidas en una competencia internacional. ¿Cuántas medallas ganó Japón?
| País | Medallas |
| Japón | MMMMM |
| Argentina | M |
| Alemania | MMMMMM |
| Egipto | MMMM |
| M = 4 medallas |
Solución
| Mira la escala de la pictografía. Cada M representa 4 medallas. | |
| \(\ 5 \cdot 4=20\) | Japón tiene 5M símbolos, por lo que el número total de medallas es\(\ 5 \cdot 4=20\). |
Japón obtuvo 20 medallas.
¿Qué tabla representa con precisión los datos que se muestran en la pictografía a continuación?
| Empleado | Salario por hora |
| Wayne | $ $ $ $ $ |
| Sarah | $ $ $ $ $ $ $ |
| Leigh | $ $ $ |
| $ = $4 |
-
Empleado Salario por hora Wayne $5 Sarah $7 Leigh $4 -
Empleado Salario por hora Wayne $20 Sarah $22 Leigh $19 -
Empleado Salario por hora Wayne $10 Sarah $14 Leigh $8 -
Empleado Salario por hora Wayne $20 Sarah $28 Leigh $16
- Contestar
-
- Identificaste el número correcto de símbolos, pero parece que olvidaste factorizar en la escala. Cada signo de dólar representa 4 dólares, así que multiplica el número de signos de dólar seguidos por 4. La respuesta correcta es el Cuadro D.
- Identificaste correctamente que Wayne gana 20 dólares, ya que la tabla indica que tiene 5 signos de dólar, y cada signo de dólar representa 4 dólares. La fila de Sarah muestra que gana siete símbolos de signo de dólar, por lo que gana 28 dólares, no 22 dólares. La respuesta correcta es el Cuadro D.
- Identificaste el número correcto de símbolos, pero parece que usaste la escala incorrecta. Cada signo de dólar representa $4, no $2. Multiplique el número de signos de dólar seguidos por 4. La respuesta correcta es el Cuadro D.
- Cada símbolo de signo de dólar representa 4 dólares, así que si multiplicas el número de signos de dólar seguidos por 4 dólares, encontrarás que Wayne gana 20 dólares, Sarah gana 28 dólares y Leigh gana 16 dólares.
Gráficos de Barras
Representar datos como imágenes tampoco siempre tiene sentido. Los gráficos de barras son una forma alternativa (y popular) de representar conjuntos de datos, especialmente aquellos con grandes cantidades de datos o que no se prestan bien a símbolos individuales. En una gráfica de barras, el número de elementos en una categoría de datos se representa por la altura o longitud de las barras.
Al igual que al leer pictografías, es esencial prestar atención a la escala: pequeñas diferencias en la altura de dos barras a veces pueden representar miles de dólares, ¡por ejemplo!
Consideremos un ejemplo. Aquí hay alguna información sobre el promedio de vida de cinco animales en estado salvaje, presentado en una tabla.
| Animal | Vida media en la naturaleza (años) |
| Zebra | 25 |
| Panda Gigante | 20 |
| Guepardo | 11 |
| Babuino | 30 |
| Elefante Africano | 70 |
Estos datos están bien en una tabla, pero presentarlos como un gráfico de barras ayuda al espectador a comparar los diferentes períodos de vida más fácilmente. Mira el gráfico de barras a continuación. En este ejemplo, los animales se listan en el lado izquierdo de la gráfica (también llamado eje y), y la vida útil en años se enumera en la parte inferior (el eje x). La gráfica muestra la información por la longitud de la barra asociada a cada nombre de animal.
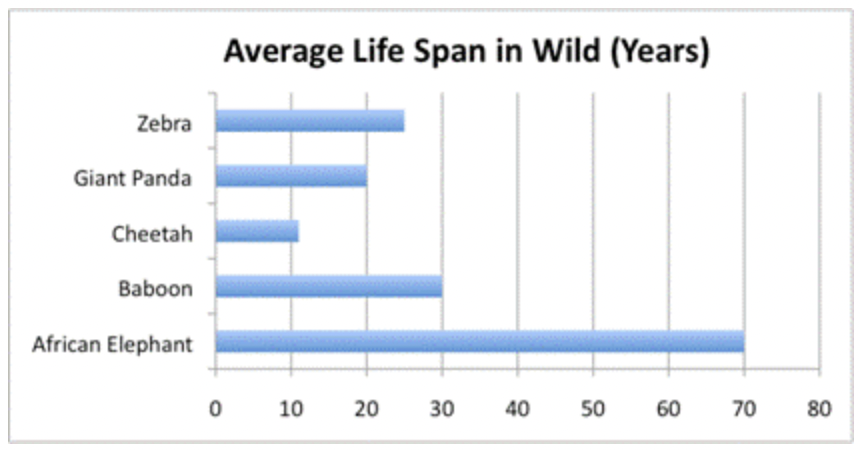
Los gráficos de barras se utilizan generalmente para comparar cantidades, no para determinar cantidades exactas, especialmente cuando la escala es grande, como en la siguiente gráfica.
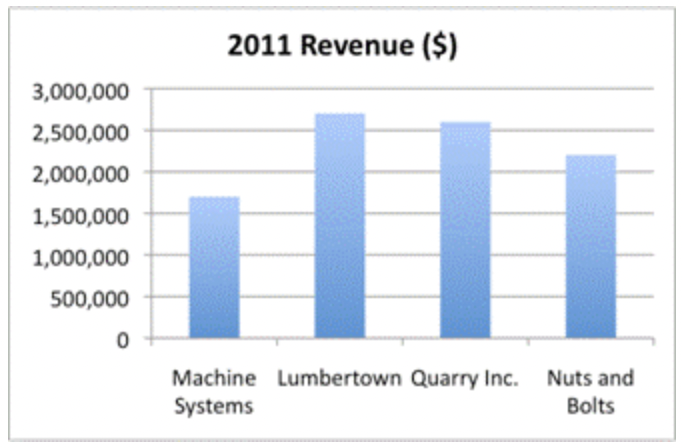
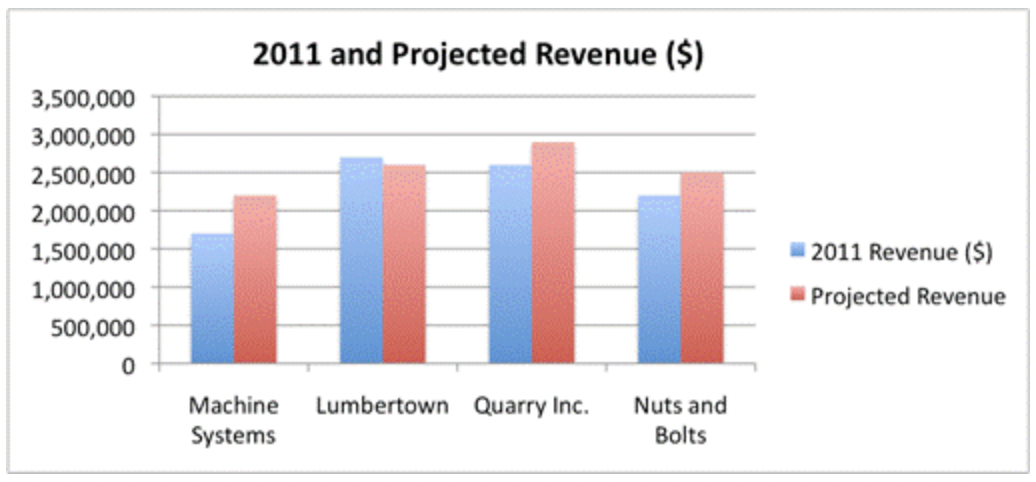
El gráfico de barras a continuación muestra los ingresos totales de cuatro empresas ficticias en 2011. Observe que la escala, en el eje y, es muy grande; cada línea horizontal representa un incremento de $500,000. Por esta razón, es difícil decir exactamente cuánto dinero ganó cada empresa en 2011. Sin embargo, comparar las barras es sencillo. Al echar un vistazo a los datos, se puede decir que Lumbertown ganó más (un poco más de $2,500,000), mientras que Machine Systems ganó lo menos (alrededor de un millón menos, con poco más de $1,500,000).
También puede usar gráficos de barras para mostrar múltiples piezas de información sobre una situación específica. Por ejemplo, mostremos los ingresos proyectados del próximo año para cada compañía en la gráfica que acabas de ver. Puedes dejar las barras existentes en la gráfica y solo agregar cuatro más.
Las columnas azules permanecen, pero ahora van acompañadas de cuatro nuevas columnas rojas que representan los ingresos proyectados para estas empresas. Nuevamente, estos datos podrían expresarse en una tabla. Con un gráfico de barras, obtienes facilidad de comparación rápida, pero pierdes el detalle de los valores exactos. Al mirar esta gráfica te dice que si bien Lumbertown tiene los ingresos más altos para 2011, se proyecta que disminuya. Por el contrario, se proyecta que Machine Systems aumente sus ingresos. Ver datos visualmente puede ayudarte a entender la historia que los datos están contando sobre una situación.
Usa la gráfica para enumerar las bebidas desde la mayor cantidad de calorías hasta la menor cantidad de calorías (tamaño de la porción: 16 onzas).
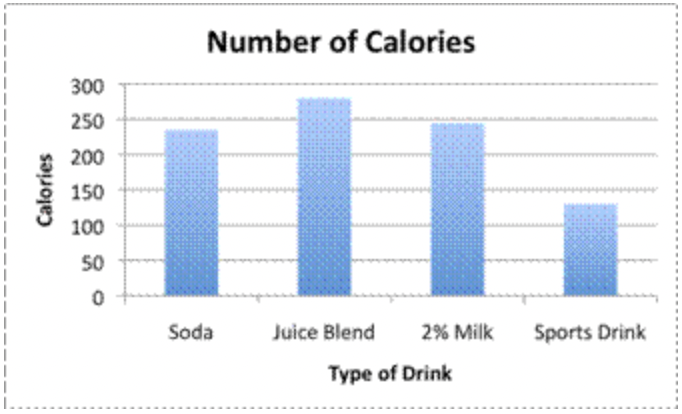
Solución
| El eje y muestra las calorías totales, y el eje x muestra la bebida. Cuanto más alto es el bar, más calorías tiene la bebida. | |
| \(\ \text { Juice Blend } \approx 275\) | La mezcla de jugo contiene más de 250 calorías, por lo que tiene la mayor cantidad de calorías por porción. |
|
\(\ 2 \% \text { Milk } \approx 245\) \(\ \text { Soda } \approx 230\) |
La soda y el 2% de leche son ambas entre 200 y 250 calorías, pero la barra para 2% de leche es más alta, por lo que debe contener más calorías. |
| \(\ \text { Sports Drink } \approx 125\) | La bebida deportiva tiene la barra más corta; contiene alrededor de 125 calorías. |
De la mayor a la menor cantidad de calorías por porción:
Mezcla de Jugos, 2% Leche, Soda, Bebida Deportiva
Con base en la gráfica a continuación, ¿qué jugador de rebote aumentó más de 2009 a 2010?
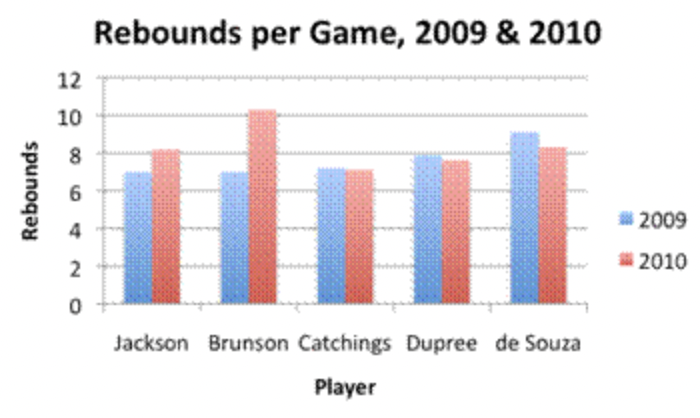
Fuente: WNBA.com, consultado en julio de 2011
Solución
| Jackson y Brunson |
El eje y muestra rebotes por juego, y el eje x muestra el nombre del jugador. Una barra más alta representa más rebotes por juego por parte del jugador. Esta gráfica muestra dos conjuntos de datos: uno para 2009, en azul, y otro para 2010, en rojo. Para comparar los datos de un año a otro, compara las alturas de las dos barras para cada jugador. Dos jugadores tuvieron promedios de rebote más altos en 2010 que en 2009. Esto se indica porque la barra roja es más alta que la barra azul. Las barras rojas de los otros jugadores son más cortas, por lo que sus rebotes disminuyeron. Comparando los tamaños de los aumentos, se puede decir que Brunson la aumentó por juego rebotando más que Jackson. |
El jugador cuyo rebote más aumentó de 2009 a 2010 fue Brunson.
Histogramas
Los conjuntos de datos que has mirado hasta ahora han mostrado datos categóricos. Los datos categóricos son datos que se pueden separar en categorías. Por ejemplo, los datos sobre el color de ojos (marrón, azul, verde), el tipo de sangre (O, A, B, AB) y el tipo de computadora que usa en el trabajo o en el hogar (PC o Mac) son todos categóricos.
Los datos cuantitativos a veces se llaman datos numéricos, porque son datos los que están representados por números. Los conjuntos de datos cuantitativos constan de cantidades como la edad (1, 2, 23, 34, 77...), las puntuaciones de las pruebas (90, 95, 100, 72...) y la altura (55 pulgadas, 50 pulgadas, 68 pulgadas,...). Observe que todos los datos aquí son números.
Los datos cuantitativos continuos se pueden graficar usando un histograma. Un histograma se asemeja a un gráfico de barras, pero en lugar de tener categorías a lo largo del eje, tiene números listados en orden y generalmente agrupados en intervalos (como 0, a 10, 11 a 20, y así sucesivamente). Si bien las barras en los gráficos de barras pueden tener espacio entre las barras, las barras de un histograma suelen estar tocándose, ya que los datos son continuos.
Veamos cómo podrías mostrar el conjunto de datos de puntaje de prueba que se enumeran a continuación.
| Nombre | Puntuación (0 a 100) |
| Alex | 81 |
| Beatriz | 73 |
| Celia | 79 |
| Donnie | 91 |
| Erykah | 87 |
| Fred | 79 |
| Gigi | 81 |
| Helene | 84 |
| Irma | 88 |
| Joelle | 96 |
Al mirar los puntajes, se puede decir que algunas personas anotaron en los 70, algunas anotaron en los 80 y otras anotaron en los 90. Se pueden organizar los datos en un histograma con los datos continuos de 0 a 100, utilizando los intervalos de 71 a 80, 81 a 90 y 91 a 100.
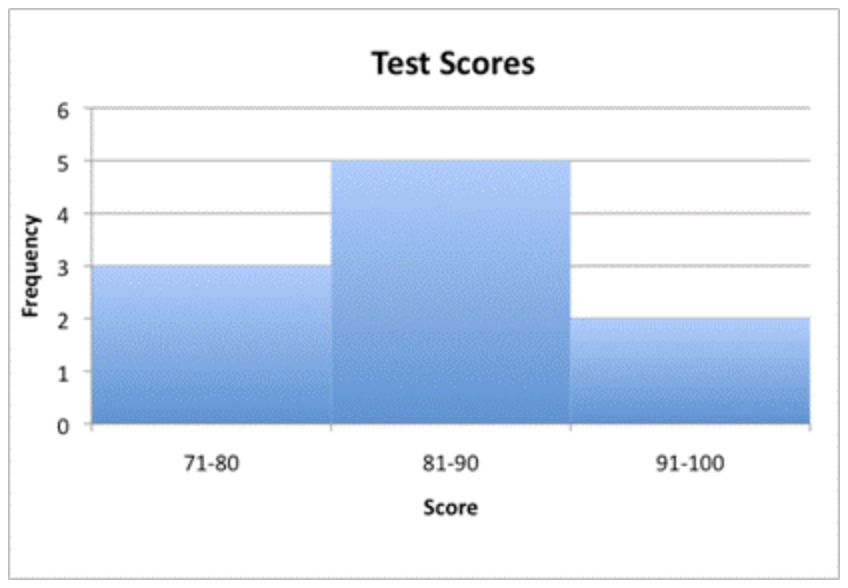
Solo hay tres intervalos para este histograma y diez puntos de datos. Para que un histograma sea significativo, debe incluir 100 puntos de datos o más y 7 intervalos o más. (Por esta razón, muchos histogramas se crean utilizando una variedad de herramientas técnicas). El histograma toma entonces formas interesantes que pueden proporcionar mucha información.
Incluso con solo 10 puntos de datos, se encuentra un histograma mucho más significativo al usar intervalos más pequeños (como 71 a 75, 76 a 80, 81 a 85, 86 a 90, 91 a 95 y 96 a 100).
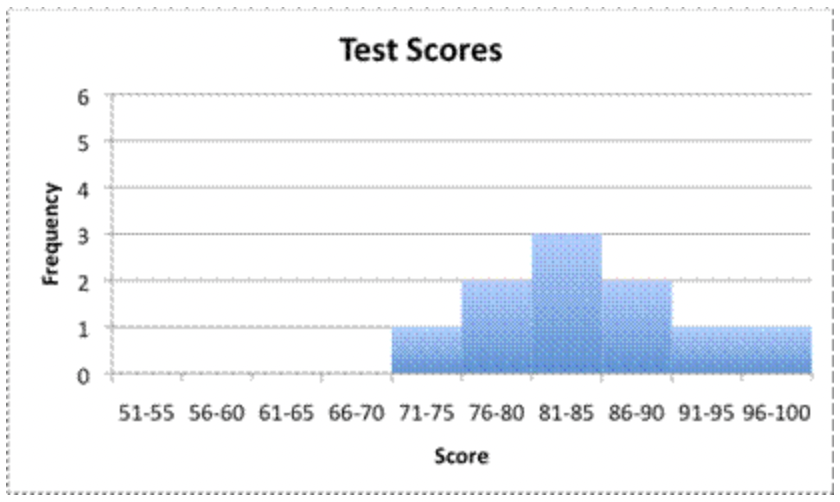
Esta segunda gráfica muestra un poco de curva a los datos. Nadie obtuvo 70 o menos, y los datos alcanzan su punto máximo en el rango de 81 a 85. Aumentar el número de intervalos tiene un efecto en la forma de la gráfica, y nos ayuda a ver algunas tendencias que se encuentran en los datos.
Con base en el siguiente histograma, ¿cuántos alumnos tienen entre 151 y 180 centímetros de altura?
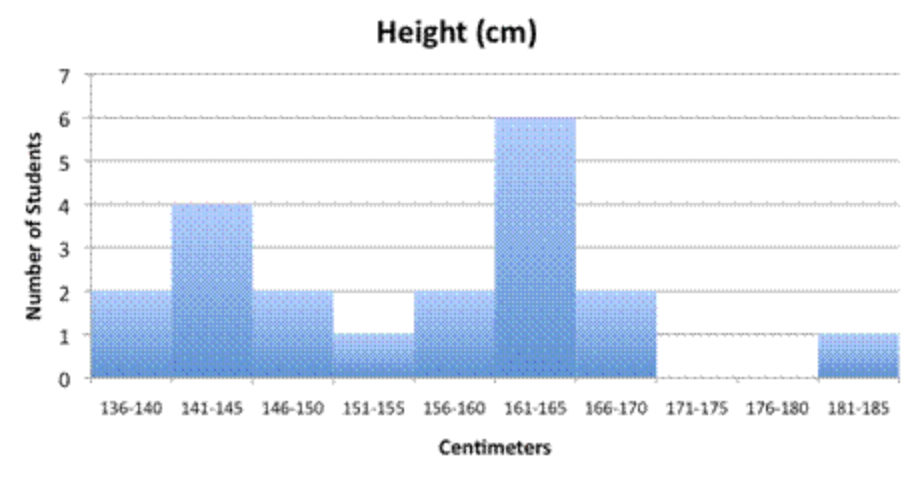
Solución
| Número de alumnos en cada intervalo: | |
| \ (\\ comenzar {matriz} {r} 151\ texto {a} 155,\ 1\\ 156\ texto {a} 160,\ 2\\ 161\ texto {a} 165,\ 6\\ 166\ texto {a} 170,\ 2\ 171\ texto {a} 175,\ 0\ 176\ text {a} 180,\ 0 \ end {array}\) |
Cada intervalo en este histograma es de 5 centímetros. |
| \(\ 1+2+6+2+0+0=11\) | Agregar el número de alumnos. |
11 alumnos miden entre 151 y 180 centímetros de altura.
Un profesor hizo este histograma para rastrear las puntuaciones en una prueba de matemáticas reciente. ¿Cuántos alumnos anotaron en el rango del 91 al 100?
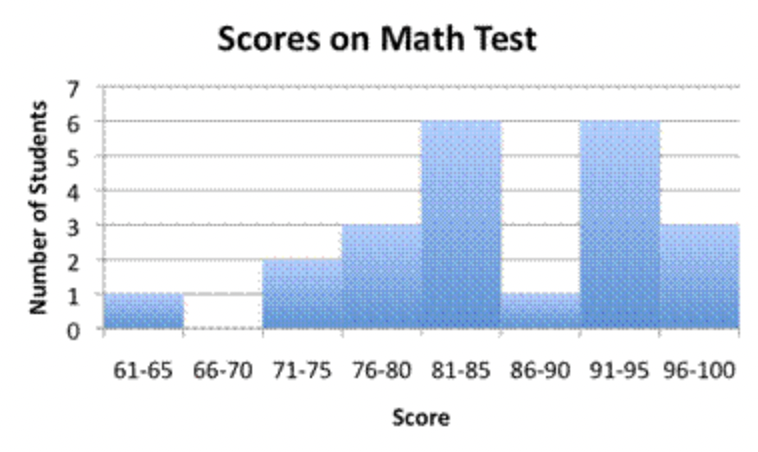
- 3
- 6
- 9
- 22
- Contestar
-
- Incorrecto. Tres alumnos anotaron entre 96 a 100 en la prueba, pero si la maestra quiere saber cuántos alumnos anotaron entre 91 y 100, entonces también tiene que considerar el número de alumnos que puntuaron entre 91 y 95. La respuesta correcta es 9.
- Incorrecto. Seis alumnos anotaron entre 91 a 95 en la prueba, pero si la maestra quiere saber cuántos alumnos anotaron entre 91 y 100, entonces también tiene que considerar el número de alumnos que obtuvieron puntajes entre 96 a 100. La respuesta correcta es 9.
- Correcto. Seis alumnos puntuaron entre 91 a 95 en la prueba, y 3 estudiantes obtuvieron entre 96 a 100. El número total de alumnos que puntuaron entre 91 a 100 es de 9.
- Incorrecto. Parece que calculaste el número total de alumnos que tomaron la prueba. Para encontrar el número que anotó entre 91 a 100, mira los intervalos de 91 a 95 y 96 a 100. La respuesta correcta es 9.
Resumen
Los datos son información matemática. Los datos matemáticos a menudo se registran en tablas para organizar, o en hojas de cálculo para organizar y ordenar. Los gráficos pueden ayudarle a ver los datos visualmente, lo que puede ayudarle a comprender mejor los datos. Una pictografía es una gráfica que utiliza símbolos para representar datos. Los gráficos de barras muestran la frecuencia de los datos categóricos, utilizando barras en lugar de símbolos. Los histogramas son similares a los gráficos de barras en que están construidos a partir de una serie de barras. Sin embargo, los histogramas representan datos cuantitativos continuos (numéricos), que pueden ilustrar tendencias así como otros atributos más avanzados.


