8.1.2: Otros Tipos de Gráficas

Objetivos de aprendizaje

• Leer e interpretar datos de gráficos circulares (gráficos circulares).
• Leer e interpretar datos a partir de gráficas de líneas simples.
• Lea e interprete los datos de las exhibiciones de tallos y hojas.

Introducción

Diferentes gráficas cuentan diferentes historias. Si bien un gráfico de barras podría ser apropiado para comparar algunos tipos de datos, hay una serie de otros tipos de gráficos que pueden presentar datos de una manera diferente. Es posible que los veas en noticias o reportajes, por lo que es útil saber leerlos e interpretarlos.

Gráficas Circulares

En ocasiones verás datos categóricos presentados en un gráfico circular, o gráfico circular. En este tipo de gráficas, las piezas individuales de datos se representan como secciones del círculo (o “pedazos del pastel”). Los gráficos circulares se utilizan a menudo para mostrar cómo un conjunto completo de datos se divide en componentes individuales.

Aquí tienes un ejemplo. Al inicio de un semestre, una maestra habla sobre cómo determinará las calificaciones de los estudiantes. Ella dice: “La mitad de tu calificación se basará en el examen final y el 20% será determinado por cuestionarios. Un proyecto de clase también valdrá 20% y la participación en clase contará para 10%”. Además de decirle a la clase esta información, también podría crear una gráfica circular.

Esta gráfica es útil porque relaciona cada parte (el examen final, los cuestionarios, el proyecto de clase y la participación en clase) con el conjunto. ¡Es fácil ver que los alumnos de esta clase tuvieron mejor estudio para el examen final!

Debido a que las gráficas circulares relacionan partes individuales y un todo, a menudo se utilizan para presupuestos y otros fines financieros. A continuación se muestra un presupuesto familiar. Se ha graficado de dos maneras: primero usando una gráfica de barras, y luego usando una gráfica circular. Cada representación ilustra la información de manera un poco diferente.

El gráfico de barras muestra las cantidades de dinero gastadas en cada artículo durante un mes. Usando estos datos, podrías averiguar cuánto necesita ganar la familia cada mes para que este presupuesto funcione.

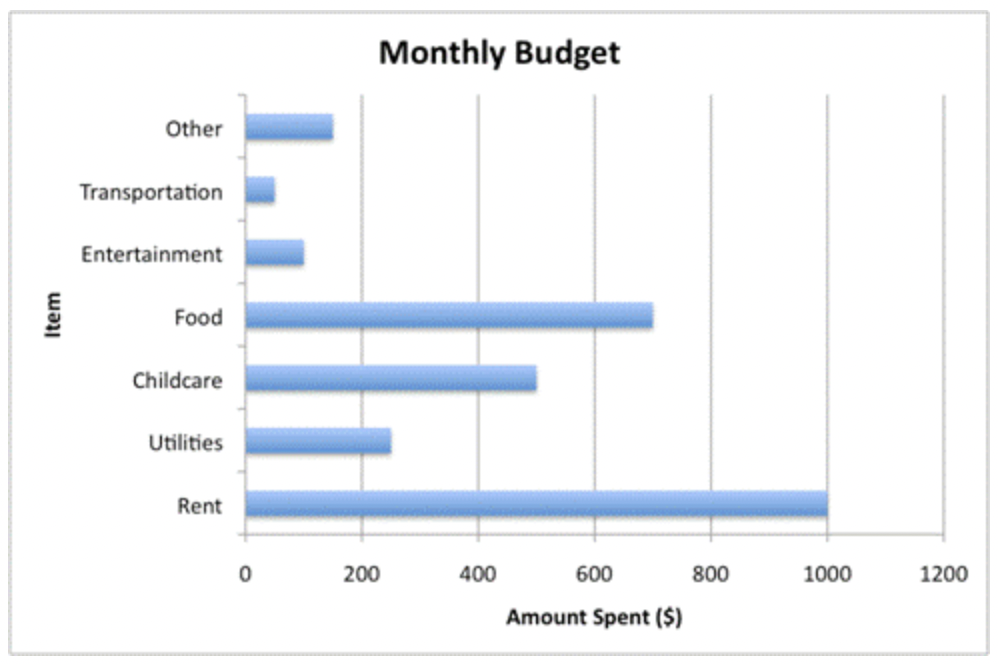
El gráfico de barras anterior se centra en la cantidad gastada para cada categoría. El gráfico circular a continuación muestra cómo cada pieza del presupuesto se relaciona con las otras piezas del presupuesto. Esto hace que sea más fácil ver hacia dónde van las mayores cantidades de dinero, y cuánto de todo el presupuesto ocupan estas piezas. La renta y la comida son los mayores gastos aquí, ya que el cuidado de niños también ocupa una porción considerable.

Si miras de cerca la gráfica circular, puedes ver que las secciones de comida, cuidado infantil y servicios públicos ocupan casi exactamente la mitad del círculo: ¡esto significa que estos tres rubros representan la mitad del presupuesto! Este tipo de análisis es más difícil de hacer con los gráficos de barras porque cada elemento se representa como su propia entidad, y no forma parte de un todo más grande.

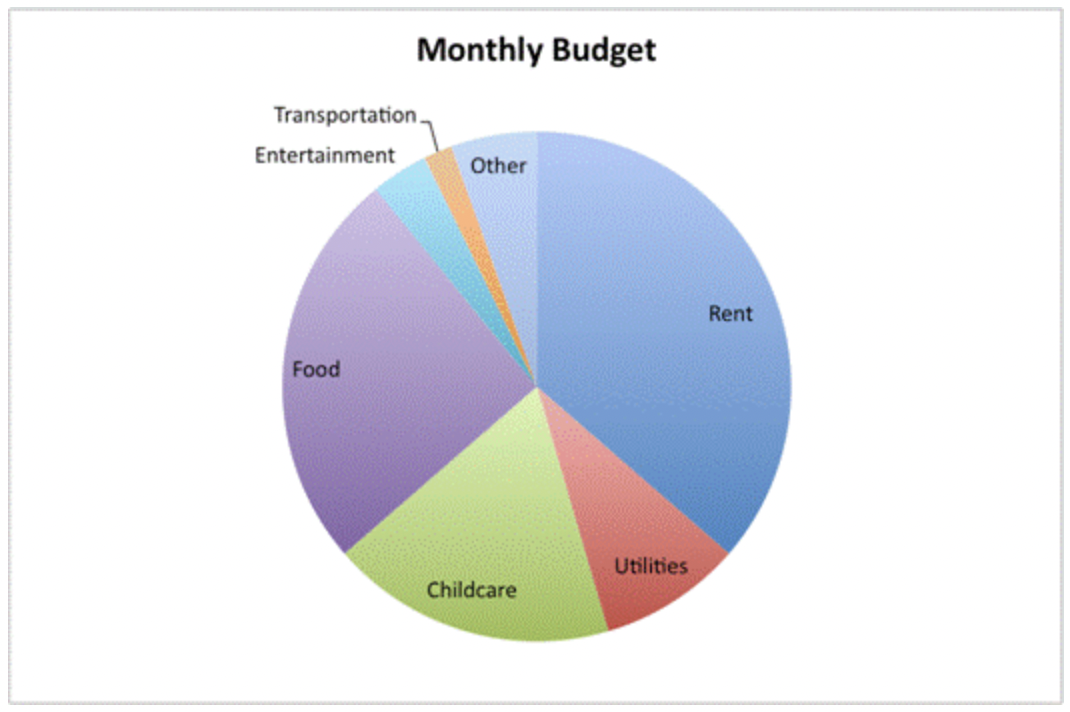
Las gráficas circulares suelen mostrar la relación de cada pieza con el conjunto utilizando porcentajes, como en el siguiente ejemplo.

Ejemplo

El gráfico circular que aparece a continuación muestra cómo pasó el día Joelle. ¿Pasó más tiempo durmiendo o haciendo trabajos relacionados con la escuela (escuela, tarea y ensayo de juego)?

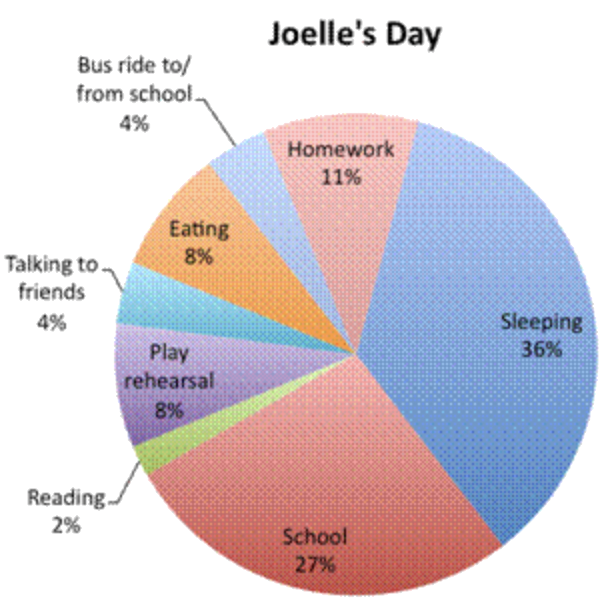
Solución

\(\ \text { Sleeping: } 36 \%\) \ (\\ begin {array} {l} \ text {Relacionado con la escuela:}\\ 27\ %+8\ %+11\ %=46\% \ end {array}\)

Mira la gráfica circular. La sección etiquetada como “Dormir” es un poco más grande que la sección llamada “Escuela” (¡y fíjate que el porcentaje de tiempo que duerme es mayor que el porcentaje de tiempo en la escuela!) “Tareas” y “Ensayo de juego” son ambos más pequeños, pero cuando los porcentajes de tiempo se agregan a “Escuela”, suman una porción mayor del día.

Joelle pasó más tiempo haciendo trabajos relacionados con la escuela.

Ejercicio

La gráfica a continuación muestra datos sobre cómo las personas en una empresa viajan al trabajo cada día.

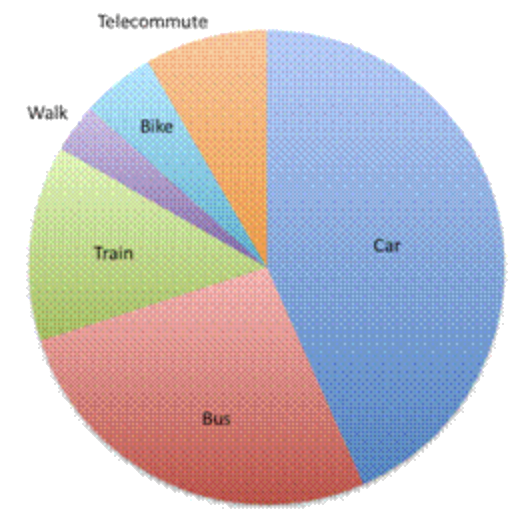
¿Qué afirmación es verdadera?

1. Todos llevan un auto, autobús o tren al trabajo.
2. Tomar el autobús es más popular que caminar o andar en bicicleta.
3. Más gente toma el tren que toma el autobús.
4. El teletrabajo es el método menos popular para viajar al trabajo.

Responder

1. Incorrecto. Mientras que la mayoría de las personas viajan en automóvil, autobús o tren, algunas viajan por otros medios, como se muestra en las otras secciones de la gráfica. La respuesta correcta es que tomar el autobús es más popular que caminar o andar en bicicleta.
2. Correcto. El gráfico muestra que alrededor de una cuarta parte de la compañía toma el autobús al trabajo, pero solo una pequeña porción de la gente camina o anda en bicicleta.
3. Incorrecto. La sección “Tren” de la gráfica circular es más pequeña que la sección “Autobús”, por lo que lo contrario es correcto: más personas toman el autobús que toman el tren. La respuesta correcta es que tomar el autobús es más popular que caminar o andar en bicicleta.
4. Incorrecto. El método de transporte menos popular es caminar, ya que tiene la rebanada más pequeña del pastel. La respuesta correcta es que tomar el autobús es más popular que caminar o andar en bicicleta.

Gráficas de líneas

A diferencia de los gráficos circulares, los gráficos de líneas generalmente se utilizan para relacionar datos durante un período de tiempo. En un gráfico de líneas, los datos se muestran como puntos individuales en una cuadrícula; una línea de tendencia conecta todos los puntos de datos.

Un uso típico de un gráfico de líneas implica el mapeo de la temperatura a lo largo del tiempo. A continuación se proporciona un ejemplo. Observe cómo se mapea la temperatura en el eje y y el tiempo se mapea en el eje x.

Cada punto de la cuadrícula muestra una relación específica entre la temperatura y el tiempo. A las 9AM, la temperatura era de 82 ^o. Se elevó a 83 ^o a las 10 AM, y luego otra vez a 85 ^o a las 11AM. Se enfrió un poco al mediodía, ya que la temperatura bajó a 82 ^o. ¿Qué pasó el resto del día?

Los datos de esta gráfica muestran que la temperatura alcanzó un máximo de 88 ^o a las 3PM. Para las 9 de la tarde de esa noche, bajaba al 72 ^o.

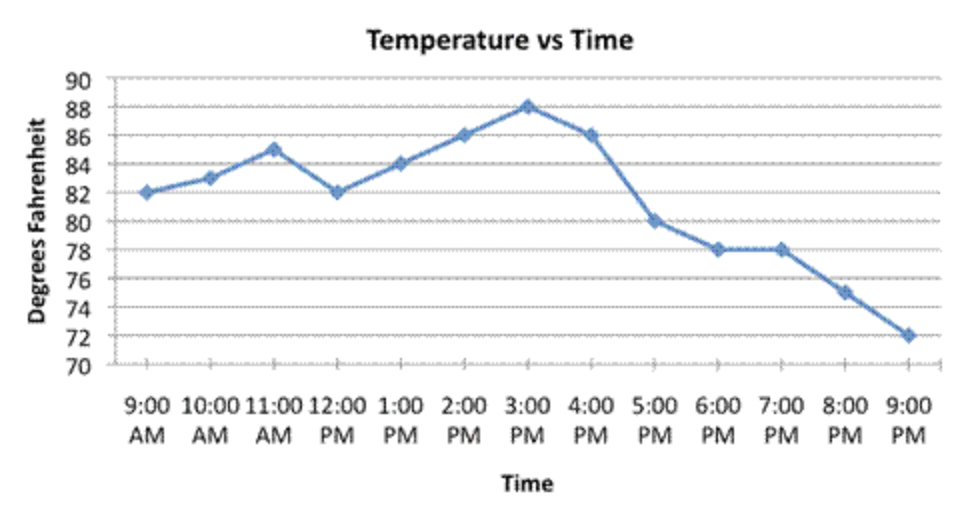
También es importante tener en cuenta los segmentos de línea que conectan cada punto de datos. Si bien esta gráfica solo proporciona puntos de datos por cada hora, podrías rastrear la temperatura cada minuto (¡o segundo!) si quisieras. Los segmentos de línea que conectan los puntos de datos indican que la relación temperatura vs. tiempo es continua, lo que significa que se puede leer en cualquier punto. Los segmentos de línea también proporcionan una estimación de cuál sería la temperatura si la temperatura se midiera en cualquier punto entre dos lecturas existentes. Por ejemplo, si quisieras estimar la temperatura a las 4:30, podrías encontrar 4:30 en el eje x y dibujar una línea vertical que pase por la línea de tendencia; el lugar donde intersecta la gráfica será la estimación de temperatura en ese momento.

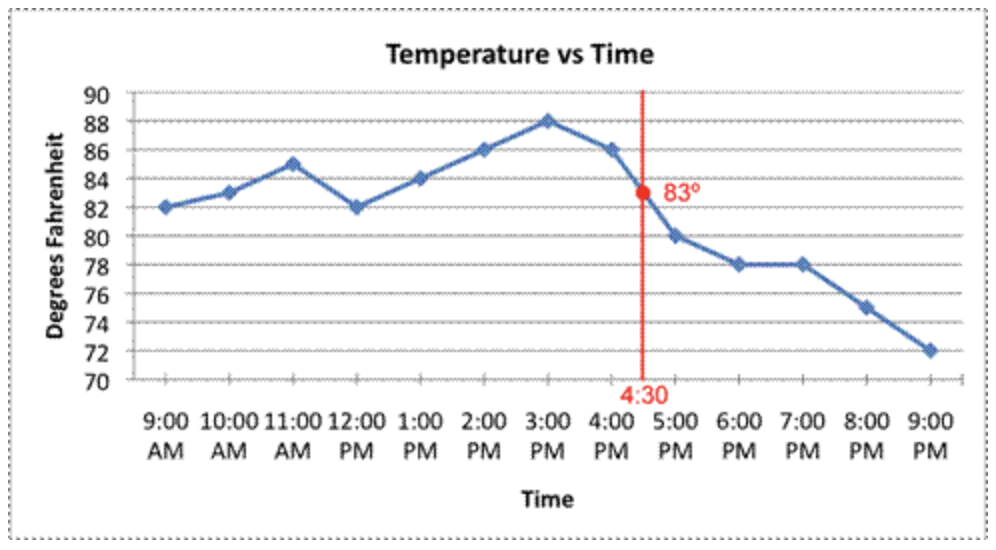
Tenga en cuenta que esto es solo una estimación basada en los datos. Hay muchas posibles fluctuaciones de temperatura entre las 4PM y las 5PM. Por ejemplo, la temperatura podría haberse mantenido estable en 86 ^o durante la mayor parte de la hora, y luego bajó bruscamente a 80 ^o justo antes de las 5PM. Alternativamente, la temperatura podría haber bajado a 76 ^o debido a una tormenta repentina, para luego volver a subir hasta los 80 ^o una vez que pasó la tormenta. En cualquiera de estos casos, ¡nuestra estimación de 83 ^o sería incorrecta! Con base en los datos, sin embargo, 83 ^o parece una predicción razonable para las 4:30 PM.

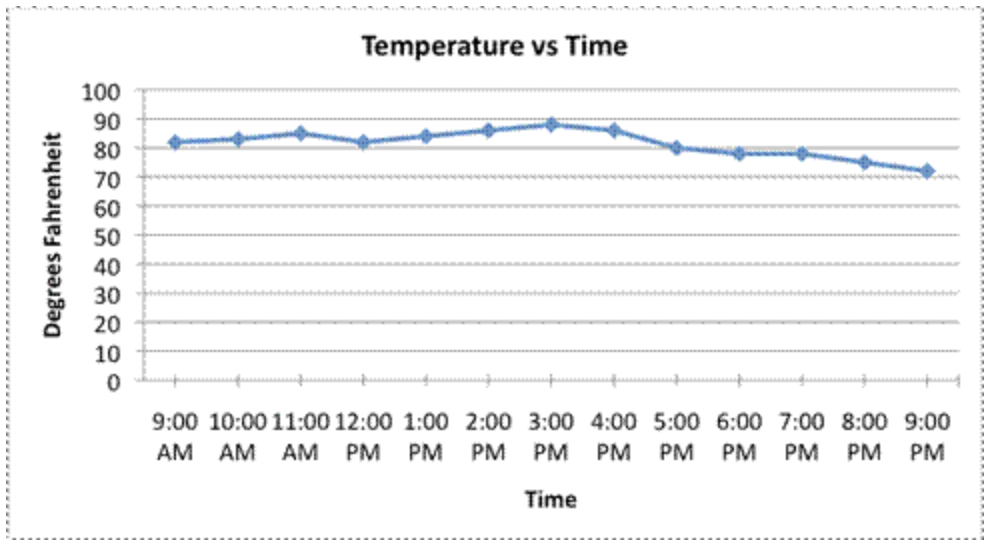
Por último, una palabra rápida sobre la escala en esta gráfica. Observe el eje y, que es la línea vertical donde se enumeran los Grados Fahrenheit. Observe que inicia a los 70 ^o, y luego aumenta en incrementos de 2 ^o cada vez. Como la escala es pequeña y la gráfica comienza a los 70 ^o, los datos de temperatura se ven bastante volátiles, ¡como si la temperatura pasara de ser cálida a caliente a muy fría! Observe el mismo conjunto de datos cuando se traza en un gráfico de líneas que comienza en 0 ^o y tiene una escala de 10 ^o.

Como puede ver, cambiar la escala de la gráfica puede afectar la forma en que un espectador percibe los datos dentro de la gráfica.

Ejemplo

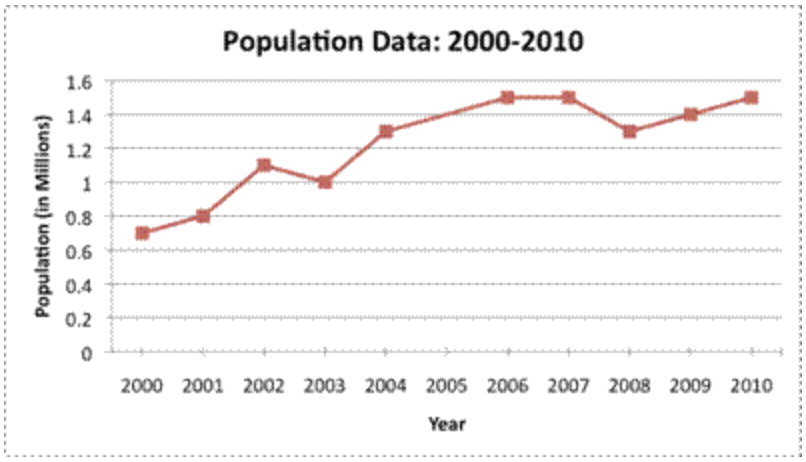
Los datos de población de una ciudad ficticia se dan a continuación. Estimar la población de la ciudad en 2005.

Solución

Mira el gráfico de líneas. La población comienza en cerca de 0.7 millones (o 700,000) en 2000, sube a 0.8 millones en 2001, y luego nuevamente a 1.1 millones en 2002. Para encontrar la población en 2005, busque 2005 en el eje x y dibuje una línea vertical que intersecta la línea de tendencia.

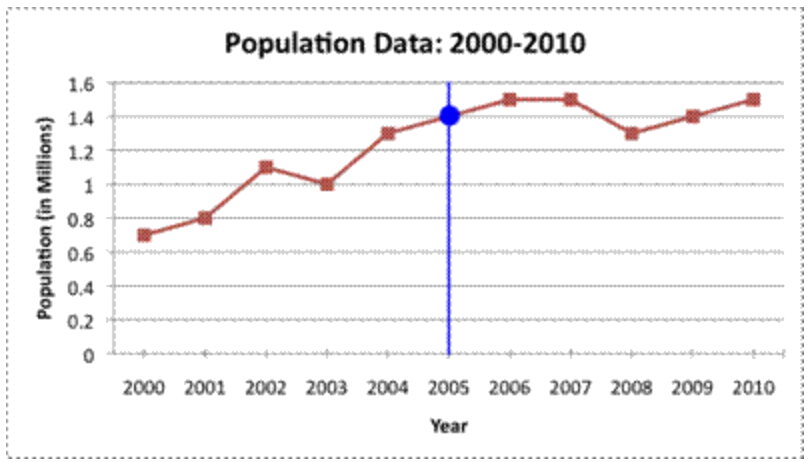
Las líneas se cruzan en 1.4, por lo que millones (o 1,400,000) serían una buena estimación.

La población en 2005 era de alrededor de 1.4 millones.

Parcelas de tallo y hoja

Una gráfica de tallo y hoja proporciona otra forma más de visualizar datos cuantitativos. Conservan los datos originales (a diferencia de las pictografías) y permiten una fácil identificación de los valores, clústeres y brechas más grandes y pequeños.

Aquí tienes un ejemplo. Un economista se pregunta sobre la cantidad de cambio sobrante que lleva la gente, y si la cantidad es mayor por la mañana o por la noche. Para recabar estos datos, se dirige a una estación del metro del centro y, una mañana, pide al azar a la gente que cuente la cantidad de cambio que tienen en su bolsillo o bolso. Ella se detiene cuando le ha preguntado 30

gente cuánto cambio están llevando. Los resultados se muestran aquí en la tabla.

Cambio de Bolsillo (en centavos)

0	85	95
50	44	81
12	25	25
15	10	5
0	76	0
59	75	73
4	94	62
42	0	60
75	15	25
31	38	50

La economista quiere tener una mejor idea de estos datos, por lo que crea una trama de tallo y hoja. En esta gráfica, el “tallo” es el dígito del diez para cada dato y la “hoja” es el dígito de uno. Si tuviera que graficar un número de tres dígitos, el tallo serían los dos primeros dígitos y la hoja sería el dígito de unos. El punto clave en una gráfica de tallo y hoja es que las hojas no contienen más de los 10 dígitos del 0 al 9.

Ella comienza por enumerar los valores de tallo, que son todos los posibles decenas dígitos: los números del 0 al 9.

Stem	Hoja
0
1
2
3
4
5
6
7
8
9

Entonces ella comienza a revisar sus datos. El primero dijo que llevaba 0 centavos. El tallo aquí es 0, y la hoja también es 0 (es importante incluir este 0 para mostrar que los datos fueron recolectados).

Stem	Hoja
0	0
1
2
3
4
5
6
7
8
9

Al mirar hacia abajo en la mesa, ve los siguientes dos datos: 50 y 12. Ella ingresa esos datos en la gráfica.

Stem	Hoja
0	0
1	2
2
3
4
5	0
6
7
8
9

El siguiente dato es 15. El tallo es 1 y la hoja es 5, por lo que pone el 5 junto al 2 que ya está en la sección de hoja de la gráfica.

Stem	Hoja
0	0
1	2 5
2
3
4
5	0
6
7
8
9

Ella continúa agregando datos hasta que tiene la siguiente trama de tallo y hoja.

Stem	Hoja
0	000045
1	0255
2	555
3	18
4	24
5	009
6	02
7	3556
8	15
9	45

De esta trama, puede ver que la mitad de las personas llevaban menos de 40 centavos (ya que hay 30 datos, el número medio es el promedio de los ítems 15 y 16. El ítem 15 es 38 y el 16 es 42, por lo que la mediana es 40.) Los datos también están bastante dispersos; no parece haber un patrón discernible sobre cuánto cambio está llevando la gente.

Esa tarde, el economista recoge datos de cambio de 30 personas más. Sin embargo, en lugar de hacer una nueva trama de tallo y hoja, reorganiza su gráfica original y agrega los nuevos datos agregando un nuevo conjunto de hojas, como se muestra aquí.

Hoja (Mañana)	Stem	Hoja (Tarde)
000045	0	0005
0255	1	05
555	2	2558
18	3	02
24	4	55
009	5	5
02	6
3556	7	0056
15	8	11368
45	9	058889

Ella nota que la forma de los datos de la tarde es diferente a la forma de los datos de la mañana. Por la mañana, mucha gente llevaba menos de 40 centavos. Por la tarde, sin embargo, la gente parecía estar cargando más cambio, con la mitad de los encuestados llevando entre 70 centavos y 99 centavos.

Ejemplo

Un biólogo utiliza una parcela de tallo y hoja para registrar las edades (en años) de diez árboles en un bosque. ¿Qué edad tenían los árboles que ella encuestó?

Stem	Hoja
5	244
6	6
7
8	0146
9	59

Solución

Stem	Hoja	Para leer una parcela de tallo y hoja, mira el tallo, luego la hoja. El primer dato tiene un tallo de 5 y una hoja de 2. Este es el número 52.
5	2 44
6	6
7
8	0146
9	59

Stem	Hoja	El segundo dato también tiene un tallo de 5 pero una hoja de 4. Este es el número 54.
5	2 44
6	6
7
8	0146
9	59

Continuar leyendo los tallos y hojas en la gráfica.

Las edades de los árboles son

52, 54, 54, 66, 80, 81, 84, 86, 95 y 99.

Ejercicio

¿Qué conjunto de números representa esta gráfica de tallo y hoja?

Stem	Hoja
0	09
1	336
2	0
3	5779

1. 0, 9, 13, 13, 16, 20, 35, 37, 37, 39
2. 0, 0, 3, 3, 5, 6, 7, 7, 9, 9
3. 0, 9, 13, 16, 20, 35, 37, 39
4. 0, 2, 31, 31, 53, 61, 73, 73, 90, 93

Responder

1. Correcto. Para encontrar el conjunto original de números a partir del cual se creó esta parcela de tallo y hoja, combine el tallo con cada una de sus hojas. El tallo será el dígito de las decenas del número, y la hoja será el dígito de unos.
2. Incorrecto. Parece que solo miraste las hojas e ignoraste los tallos. Para encontrar el conjunto original de números a partir del cual se creó esta parcela de tallo y hoja, combine el tallo con cada una de sus hojas: el tallo será el dígito de las decenas del número, y la hoja será el dígito de unos. La respuesta correcta es 0, 9, 13, 13, 16, 20, 35, 37, 37, 39.
3. Incorrecto. Parece que sabes cómo crear el conjunto de datos a partir de la gráfica de tallo y hoja, pero equivocadamente sacaste los valores repetidos en el conjunto de datos. Todos los puntos de datos, incluso los repetidos, son necesarios. La respuesta correcta es 0, 9, 13, 13, 16, 20, 35, 37, 37, 39.
4. Incorrecto. ¡Parece que invertiste el tallo y la hoja! Para encontrar el conjunto original de números a partir del cual se creó esta parcela de tallo y hoja, combine el tallo con cada una de sus hojas: el tallo será el dígito de las decenas del número, y la hoja será el dígito de unos. La respuesta correcta es 0, 9, 13, 13, 16, 20, 35, 37, 37, 39.

Resumen

Los gráficos de barras son solo el comienzo de la historia cuando se trata de visualizar conjuntos de datos. Los gráficos circulares muestran cómo se divide un conjunto de datos en secciones, y ayudan al espectador a visualizar cómo cada sección se relaciona con el todo. Por el contrario, los gráficos de líneas generalmente se utilizan para relacionar datos continuos durante un período de tiempo. Un tercer tipo de gráfica, la gráfica de tallo y hoja, proporciona otra forma de organizar los datos cuantitativos. Las gráficas de tallo y hoja son útiles para obtener una imagen rápida de los valores más pequeños y mayores, los clústeres y las brechas de los datos dentro de un conjunto.