8.2.1: Medidas de Centro
- Page ID
- 111405
- Encuentra la media, mediana y modo de un conjunto de números.
- Encuentre el rango y rango medio de un conjunto de datos.
- Lea e interprete datos de gráficas de cajas y bigotes.
- Resolver problemas de aplicación que requieran el cálculo de la media, mediana, rango o rango medio.
Introducción
La media, la mediana y el modo son herramientas importantes en la caja de herramientas del estadístico. Todas estas medidas del centro utilizan puntos de datos para aproximar y comprender un “valor medio” o “promedio” de un conjunto de datos dado. Dos medidas más de interés son el rango y el rango medio, que utilizan los valores mayores y menores del conjunto de datos para ayudar a describir la propagación de los datos.
Entonces, ¿por qué necesitarías averiguar la mitad de un conjunto de datos? Y ¿por qué necesitas tres medidas en lugar de solo una? Veamos de cerca estas medidas de centro y aprendamos cómo pueden ayudarnos a entender conjuntos de datos.
Media, Mediana y Modo
“Media” es un término matemático para “promedio” que quizás ya conozcas. También conocida como la “media aritmética”, se encuentra sumando todos los valores de datos en un conjunto y dividiendo esa suma por el número de elementos de datos.
A menudo puedes encontrar en tu cabeza el promedio de dos números familiares, como el 10 y el 16, sin mucho cálculo. ¿Qué número se encuentra a mitad de camino entre ellos? 13. Sin embargo, una forma matemática de resolver esto es sumar 10 y 16 (lo que le da 26) y luego dividirlo por 2 (ya que hay 2 números en el conjunto de datos). \(\ 26 \div 2=13\)
Conocer el proceso ayuda cuando necesitas encontrar la media de más de dos números. Por ejemplo, si te piden encontrar la media de los números 2, 5, 3, 4, 5 y 5, primero encuentra la suma: 2 + 5 + 3 + 4 + 5 + 5 = 24. Entonces, divida esta suma por el número de números en el conjunto, que es 6. Entonces la media de los datos es\(\ 24 \div 6\), o 4.
En el conjunto de datos anterior, observe que la media era 4 y que el conjunto también contenía un valor de 4. Esto no siempre ocurre. En el ejemplo que sigue, la media es 18, aunque 18 no está en el conjunto de datos en absoluto.
Encuentra la media del conjunto: 4, 7, 28, 33.
Solución
| \(\ 4+7+28+33=72\) | Sumar todos los valores. |
| \(\ \frac{72}{4}=18\) | Dividir por 4, el número de valores. |
La media es 18.
A continuación, veamos la “mediana”. La mediana es el valor medio cuando se ordenan los datos. Si hay dos valores medios, la mediana es el promedio de los dos valores medios.
Para calcular la mediana, primero pones tus datos en orden numérico de menor a mayor. Luego identifique el valor (s) medio (s).
Por ejemplo, veamos los siguientes valores: 4, 5, 1, 3, 2, 7, 6. Para encontrar la mediana de este conjunto, lo pondrías en orden de menor a mayor.
\ (\\ begin {array} {lllllll}
1 & 2 & 3 &\ bf4 & 5 & 6 & 7
\ end {array}\)
Después identificar el valor medio. Hay tres valores a la derecha de cuatro y tres valores a la izquierda de cuatro. El valor medio es 4, por lo que 4 es la mediana.
Sin embargo, si hay un número par de elementos de datos, la mediana será la media de los dos elementos de datos del centro.
Encuentra la mediana del conjunto: 2, 5, 3, 4, 5, 5
Solución
| \(\ 2,3,4,5,5,5\) | Organizar los valores de menor a mayor. |
|
\(\ 2,3, \mathbf{4}, \mathbf{5}, 5,5\) \(\ \frac{9}{2}=4.5\) |
El conjunto tiene 2 valores medios, 4 y 5. Así que toma la media (promedio) de los dos valores. |
La mediana es 4.5.
Por último, consideremos el “modo”. El modo se encuentra buscando el valor de datos que aparece con mayor frecuencia. Si hay un empate bidireccional para la mayoría de las veces, los datos son bimodales y se utilizan ambos valores de datos como modos. A veces no hay modo. Esto sucede cuando no hay valor de datos que ocurre con mayor frecuencia. En nuestro conjunto de datos de ejemplo (2, 3, 4, 5, 5, 5), el número 5 aparece 3 veces y todos los demás números aparecen una vez, por lo que el modo es 5.
Encuentra el modo del conjunto: 12, 4, 12, 5, 5, 8, 12, 0, 1, 12
Solución
| 0, 1, 4, 5, 5, 8, 12, 12, 12, 12, 12 | Organizar los valores de menor a mayor (aunque este no es un paso necesario, a veces ayuda a encontrar el modo si los números están dispuestos en orden ascendente). |
| 0, 1, 4, 5, 5, 8, 12, 12, 12, 12, 12 | 0, 1, 4, 5, 5, 8, 12, 12, 12, 12, 12 |
El modo es 12.
Veamos un ejemplo con algunos datos relevantes.
Carlos recibió los siguientes puntajes en sus exámenes de matemáticas: 84, 92, 74, 98 y 82. Encuentra la media, mediana y modo de sus puntuaciones.
Solución
| \(\ \frac{84+92+74+98+82}{5}\) | Para encontrar la media, sumar todos los puntajes de los exámenes juntos y dividir por el número de pruebas. |
| \(\ \frac{430}{5}=86\) | La media es 86. |
| \(\ 74,82,84,92,98\) | Para encontrar la mediana, ordene los puntajes de las pruebas de menor a mayor. |
| \(\ 84\) | Hay cinco puntajes, por lo que el puntaje medio de la prueba es el tercero en la lista ordenada. Esta es la mediana. |
| \(\ 74,82,84,92,98\) | Dado que cada número aparece exactamente una vez, no hay modo. |
La media es 86.
La mediana es 84.
No hay modo.
¿Qué se puede aprender de la media, mediana y modo de los puntajes de los exámenes de Carlos? Observe que estos valores no son los mismos.
Tanto la media como la mediana nos dan una imagen de cómo le va a Carlos. Al observar estas medidas, se nota que la mitad del conjunto de datos está a mediados de los 80: el valor medio es 86 y el valor medio es 84. Eso es todo lo que realmente buscas al usar la mediana y la media: encontrar el centro, o medio, de los datos. Observe, también, que no hay modo, ya que Carlos no anotó lo mismo en dos pruebas. En el caso de la toma de exámenes, el modo suele carecer de sentido, a menos que haya muchos 0s, lo que podría significar que el alumno no hizo su tarea, ¡o realmente no sabe lo que está pasando!
Encuentra la media, mediana y modo del siguiente conjunto de números: 12, 11, 13, 11, 12, 10, 10, 11, 13, 14
Solución
| \(\ \frac{12+11+13+11+12+10+10+11+13+14}{10}=\frac{117}{10}=11.7\) | Para encontrar la media, sumar todos los números y dividir esa suma por el número de números. |
| \(\ 10,10,11,11,11,12,12,13,13,14\) | Para encontrar la mediana, primero ordene los números de menor a mayor. |
| \(\ \frac{11+12}{2}=\frac{23}{2}=11.5\) | Dado que hay 10 números (un número par) la mediana es la media de los dos números medios (el 5 y el 6), o a mitad de camino entre 11 y 12. |
| \(\ 10,10, \mathbf{1 1}, \mathbf{1 1}, \mathbf{1 1}, 12,12,13,13,14\) | Para encontrar el modo, busca el número que aparece con más frecuencia. |
| \(\ 11\) | El número 11 aparece con mayor frecuencia, 3 veces. |
La media es 11.7.
La mediana es 11.5.
El modo es 11.
En este caso, la media, la mediana y el modo son muy cercanos en valor. Esto muestra cierta consistencia en los datos, con un valor medio (promedio) de alrededor de 11. Si estos datos representaran las edades de los estudiantes en un equipo de ajedrez, por ejemplo, tendrías una buena idea de que todos en el equipo tenían alrededor de 11 años, con algunos miembros mayores y más jóvenes.
Durante un periodo de siete días en julio, un meteorólogo registró que la temperatura alta media diaria fue de 91 o.
¿Cuáles de las siguientes son afirmaciones verdaderas?
- La temperatura alta fue exactamente de 91 o en cada uno de los siete días.
- La temperatura alta nunca fue inferior a 92 o.
- La mitad de las altas temperaturas estuvieron por encima de 91 o y la mitad estaban por debajo de 91 o.
- 1 solo
- 2 solamente
- 3 solamente
- 1, 2 y 3
- Responder
-
- Incorrecto. El hecho de que la mediana alta fuera de 91 o no significa que la temperatura alcanzara los 91 o en cada día. La respuesta correcta es la declaración 3 solamente.
- Incorrecto. Se sabe que la mediana es de 91 o, por lo que 91 o es miembro del conjunto de datos, lo que significa que la temperatura tuvo que haber sido inferior a 92 o al menos una vez durante la semana. La respuesta correcta es la declaración 3 solamente.
- Correcto. La mitad de las altas temperaturas estuvieron por encima de 91 o y la mitad estuvieron por debajo de 91 o ya que la mediana siempre representará el valor donde la mitad de los datos es mayor y la mitad los datos son menores.
- Incorrecto. El enunciado 1 es incorrecto porque una mediana máxima de 91 o no significa necesariamente que la temperatura alcanzó los 91 o en cada día. El enunciado 2 es incorrecto porque sabes que la mediana es de 91 o, por lo que 91 o es miembro del conjunto de datos, lo que significa que la temperatura tuvo que haber sido inferior a 92 o al menos una vez durante la semana. La respuesta correcta es la declaración 3 solamente.
Rango y rango medio
Existen otras medidas útiles distintas de la media, la mediana y el modo para ayudarle a analizar un conjunto de datos. Al mirar los datos, a menudo se quiere entender la propagación de los datos: la brecha entre el mayor número y el menor número. Este es el rango de los datos. Para encontrar el rango, reste el menor valor del conjunto de datos del mayor valor. Por ejemplo, en los datos de 2, 5, 3, 4, 5 y 5, el menor valor es 2 y el mayor valor es 5, por lo que el rango es 5-2, o 3.
También es útil saber qué número está a medio camino entre el menor valor y el mayor valor del conjunto de datos. Este número se llama el rango medio. Para encontrar el rango medio, sumar los valores menores y mayores y dividir por dos, o en otras palabras, encontrar la media de los valores menores y mayores.
El rango medio de 2, 5, 3, 4, 5 y 5 es\(\ \frac{2+5}{2}=\frac{7}{2}=3.5\).
Veamos un par de ejemplos.
Encuentra el rango y rango medio para el siguiente conjunto de números: 2, 4, 7, 10, 14, 35.
Solución
| rango:\(\ 35-2=33\) | Restar el menor valor del mayor valor para encontrar el rango. |
| rango medio:\(\ \frac{35+2}{2}=\frac{37}{2}=18.5\) | Sumar el mayor valor y el menor valor y dividir por 2. |
El rango es 33.
El rango medio es de 18.5.
Encuentra el rango y rango medio para el siguiente conjunto de números: 62, 88, 20, 145, 37, 105, 93, 22.
Solución
|
número mínimo: 20 mayor número: 145 |
Dado que el conjunto de datos no está ordenado de menor a mayor, identifique los números menores y mayores. |
| Rango: 145-20=125 | Restar el menor valor del mayor valor para encontrar el rango. |
| rango medio:\(\ \frac{145+20}{2}=\frac{165}{2}=82.5\) | Sumar el mayor valor y el menor valor y dividir por 2. |
El rango es de 125.
El rango medio es de 82.5.
Parcelas de caja y bigotes
Otro tipo de gráfico que podrías ver se llama trama de caja y bigotes. Estas gráficas proporcionan una manera visual de entender tanto el rango como el medio de un conjunto de datos.
Aquí hay un conjunto de muestra de 15 números para que empecemos.
12, 5, 18, 20, 11, 9, 3, 5, 7, 18, 12, 15, 6, 10, 11
Crear una gráfica de caja y bigotes a partir de estos datos requiere encontrar la mediana del conjunto. Para ello, ordene los datos.
3, 5, 5, 6, 7, 9, 10, 11, 11, 12, 12, 15, 18, 18, 20
Este conjunto de datos tiene 15 números, por lo que la mediana será el número 8 en el conjunto: 11.
Encontrar la mediana del conjunto de datos esencialmente lo divide en dos: un conjunto de números por debajo de la mediana y un conjunto de números por encima de la mediana. ¡Una trama de caja y bigotes requiere que también encuentres la mediana de estos números!
Juego inferior: 3, 5, 5, 6, 7, 9, 10. Mediana: 6
Juego superior: 11, 12, 12, 15, 18, 18, 20. Mediana: 15
Entonces, la mediana del conjunto es 11, la mediana de la mitad inferior es 6, y la mediana de la mitad superior es 15.
3, 5, 5, 6, 7, 9, 10, 11, 11, 12, 12, 15, 18, 18, 20
Aquí se muestra una gráfica de caja y bigotes para este conjunto de datos. ¿Observa alguna similitud entre los números anteriores y la ubicación de la caja?
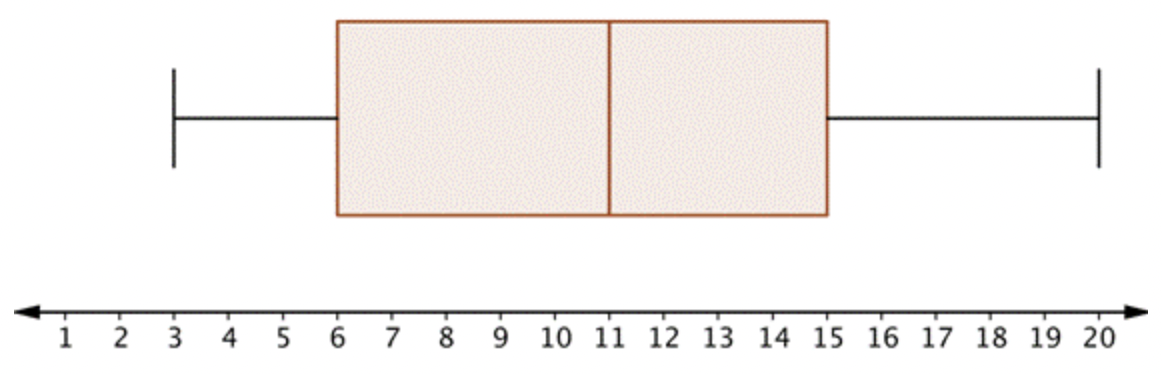
Observe que una “caja” (sección rectangular) comienza en 6 (la mediana del conjunto inferior) y va a 11 (la mediana del conjunto completo), y la otra caja va de 11 a 15 (la mediana del conjunto superior).
Los “bigotes” son los segmentos de línea en cada extremo. Uno se extiende de 3 (el menor valor en el conjunto) a 6, y el otro va de 15 a 20 (el mayor valor en el conjunto).
La gráfica de caja y bigotes divide esencialmente el conjunto de datos en cuatro secciones (o cuartiles): bigotes, caja, caja, bigotes. El tamaño de los cuartiles puede ser diferente, pero el número de puntos de datos en cada cuartil es el mismo.
Puede usar una gráfica de caja y bigotes para analizar cómo se distribuyen los datos de un conjunto. También puedes usar las gráficas de caja y bigotes para comparar dos conjuntos de datos.
Uso de Medidas de Centro para Resolver Problemas
El uso de media, mediana y modo, así como rango y rango medio puede ayudarte a analizar situaciones y tomar decisiones sobre cosas como cuál es la mejor, ya sea más confiable caminar o tomar el autobús a la escuela, o incluso si comprar o vender acciones en particular en el mercado de valores.
Veamos un ejemplo de cómo analizar datos usando medidas de centro puede ayudarte a tomar decisiones (¡e incluso llegar a la escuela a tiempo!).
A continuación se muestra una tabla que enumera la cantidad de tiempo que tardó Marta en llegar a la escuela ya sea en autobús o caminando, en 12 días separados. Los tiempos son puerta a puerta, es decir, el reloj comienza cuando sale de su puerta principal y termina cuando entra a la escuela.
| Bus | Caminando |
| 16 minutos | 22 minutos |
| 14 minutos | 19 minutos |
| 15 minutos | 21 minutos |
| 14 minutos | 20 minutos |
| 31 minutos | 21 minutos |
| 15 minutos | 20 minutos |
- ¿Qué método de viaje es más rápido?
- Si sale de su casa 25 minutos antes de que comience la escuela, ¿debería caminar o tomar el autobús para estar segura de llegar a la escuela a tiempo?
Solución
|
autobús:\(\ \frac{16+14+15+14+31+15}{6}=17.5\) caminando:\(\ \frac{22+19+21+20+21+20}{6}=20.5\) |
Determinar la media de cada método de viaje. |
|
autobús:\(\ 31-14=17\) caminando:\(\ 22-19=3\) |
Determinar el rango de cada método de viaje. |
|
autobús:\(\ 14,14,15,15,16,31\) \(\ \frac{15+15}{2}=15\) caminando:\(\ 19,20,20,21,21,22\) \(\ \frac{20+21}{2}=20.5\) |
Determinar la mediana para cada método de viaje. |
|
autobús:\(\ 14,15\) caminando:\(\ 20,21\) |
Determinar el modo para cada método de viaje. |
| Bus | Caminando | |
| Media | 17.5 | 20.5 |
| Mediana | 15 | 20.5 |
| Modo | 14, 15 | 20, 21 |
| Rango | 17 | 3 |
Mirando la media, la mediana y el modo, la forma más rápida de ir a la escuela es viajar en autobús. Los datos también muestran que el autobús es el más variable, con un rango de 17, por lo que si Marta quiere estar segura de que llega a tiempo a la escuela, debe caminar.
En el ejemplo anterior, viajar en autobús es, en promedio, un camino más rápido a la escuela que caminar. Esto se revela en la media de cada método, lo que demuestra que el autobús es 3 minutos más rápido. El modo y la mediana muestran una ventaja de tiempo aún mayor para viajar en autobús, y esto se debe al valor único alto de 31 minutos que realmente no se tiene en cuenta en estas medidas. Observe la diferencia en la media (17.5) y la mediana (15) para viajar en autobús, lo que le permite saber que hay alguna varianza en los datos.
En lo que respecta a llegar a la escuela a tiempo, si bien no es el método más rápido, caminar es el más confiable, con valores consistentes para media, mediana y modo, y un valor bajo para el rango, lo que significa que la dispersión de los datos es muy pequeña.
Veamos otro ejemplo.
Los tres mejores tenistas masculinos durante julio de los años 2007 a 2011 fueron (sin ningún orden en particular), Roger Federer, Rafael Nadal y Novak Djokovic. Con base en sus clasificaciones de julio, ¿quién ha sido el mejor intérprete en este lapso de tiempo?
| julio | Nadal | Federer | Djokovic |
| 2011 | 2 | 3 | 1 |
| 2010 | 1 | 3 | 2 |
| 2009 | 2 | 1 | 4 |
| 2008 | 2 | 1 | 3 |
| 2007 | 2 | 1 | 3 |
Datos tomados de ATP World Tour, agosto de 2011
Solución
|
Nadal:\(\ \frac{2+1+2+2+2}{5}=\frac{9}{5}=1.8\) Federer:\(\ \frac{3+3+1+1+1}{5}=\frac{9}{5}=1.8\) Djokovic:\(\ \frac{1+2+4+3+3}{5}=\frac{13}{5}=2.6\) |
Encuentra la media del ranking de cada jugador. |
|
Nadal:\(\ 1,2,2,2,2=2\) Federer:\(\ 1,1,1,3,3=1\) Djokovic:\(\ 1,2,3,3,4=3\) |
Encuentra la mediana del ranking de cada jugador. |
|
Nadal:\(\ 1,2,2,2,2=2\) Federer:\(\ 1,1,1,3,3=1\) Djokovic:\(\ 1,2,3,3,4=3\) |
Encuentra el modo de clasificación de cada jugador. |
|
Nadal:\(\ 2-1=1\) Federer:\(\ 3-1=2\) Djokovic:\(\ 4-1=3\) |
Encuentra el rango de clasificación de cada jugador. |
Parece que Nadal y Federer están prácticamente empatados para el mejor intérprete a lo largo de esos 5 años, con Djokovic en tercer lugar. El ranking medio de Nadal y Federer es 1.8, así que incluso están ahí. Y si bien el ranking de Federer tiene una mediana de 1 y una modalidad de 1 (superando a Nadal en ambas ocasiones), también tiene un rango más amplio: Federer ha pasado algún tiempo en el 3er lugar, lo que Nadal no tiene.
Dependiendo de tu punto de vista (¡y tu preferencia de jugador!) , se podría argumentar que ya sea Federer o Nadal es mejor que el otro, pero los datos parecen mostrar que son casi iguales. Claramente, con el tiempo, la actuación de Nadal y Federer es muy cercana, con la media de sus rankings idéntica. La media probablemente da la mejor evaluación del desempeño general, pero no nos cuenta toda la historia. Usando el rango, Nadal ha sido más consistente que Federer, aunque tiene menos clasificaciones número uno. No se muestra en ninguna de estas medidas cómo el ranking de Djokovic se ha ido moviendo al alza y el ranking de Federer se ha ido moviendo a la baja. También vale la pena señalar que es difícil llegar a una conclusión con una cantidad tan pequeña de datos; usar otras medidas, como los torneos ganados y el ranking promedio de oponentes también puede ayudarte a entender quién fue el mejor jugador en este tiempo.
Resumen
Las medidas del centro te ayudan a analizar datos numéricos. La media (o media aritmética) a menudo se denomina “promedio” y se encuentra dividiendo la suma de los elementos de datos por el número de ítems. La mediana es el número que está en el medio cuando los datos se ordenan de menor a mayor, y el modo es el número que aparece con mayor frecuencia. El rango es la diferencia entre el menor número y el mayor número, y el rango medio es la media del mayor valor y el menor valor. Las gráficas de caja y bigotes utilizan la mediana y el rango para ayudarle a interpretar los datos visualmente.


