9.2.1: Sumando enteros

Última actualización
Guardar como PDF

Page ID: 111338

The NROC Project

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

Agrega dos o más enteros con el mismo signo.
Agrega dos o más enteros con signos diferentes.

Introducción

En un día extremadamente frío, la temperatura puede ser -10. Si la temperatura sube 8 grados, ¿cómo va a encontrar la nueva temperatura? Saber sumar enteros es importante aquí y en gran parte del álgebra.

Agregar números enteros con el mismo signo

Dado que los enteros positivos son los mismos que los números naturales, sumar dos enteros positivos es lo mismo que sumar dos números naturales. Para agregar enteros positivos en la recta numérica, se mueve hacia la derecha (en la dirección positiva).

Actividad interactiva suplementaria

Pruebe la línea numérica interactiva a continuación. Elija algunos pares de enteros positivos para agregar. Haga clic y arrastre los puntos azules y rojos, y observe cómo funciona la adición.

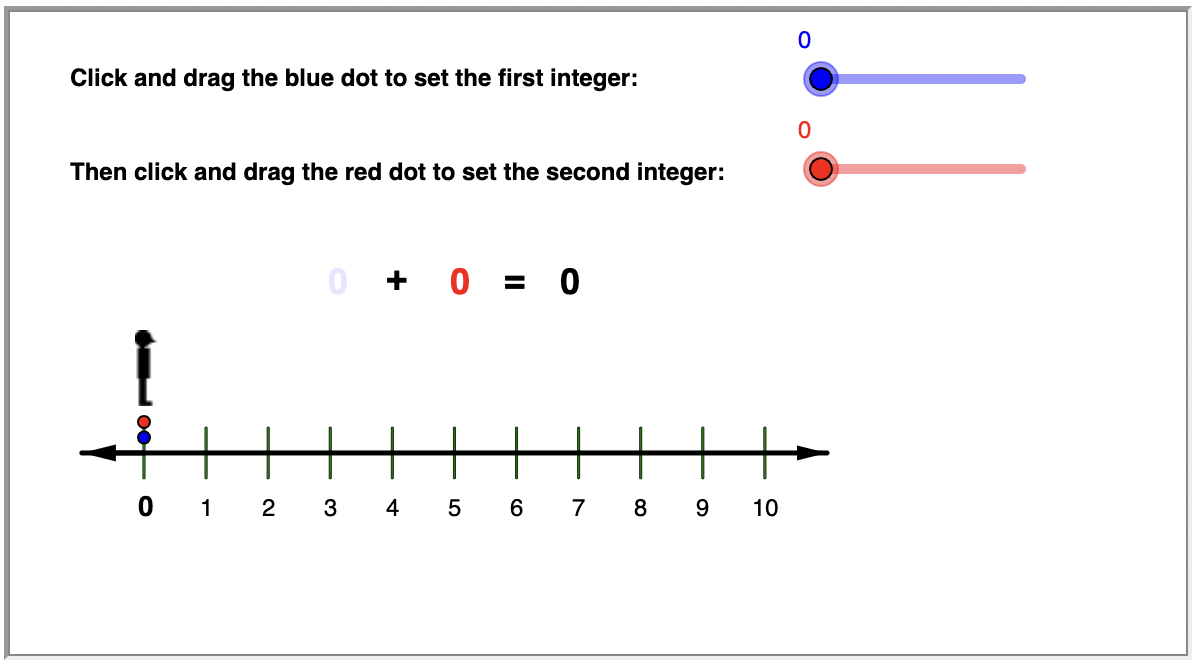
$Screen Shot 2021-05-20 a las 8.29.58 PM.png$

Para agregar números enteros negativos en una recta numérica, se mueve hacia la izquierda (en la dirección negativa).

Actividad interactiva suplementaria

Pruebe la línea numérica interactiva a continuación. Elija algunos pares de enteros negativos para agregar. Haga clic y arrastre los puntos azules y rojos, y observe cómo funciona la resta.

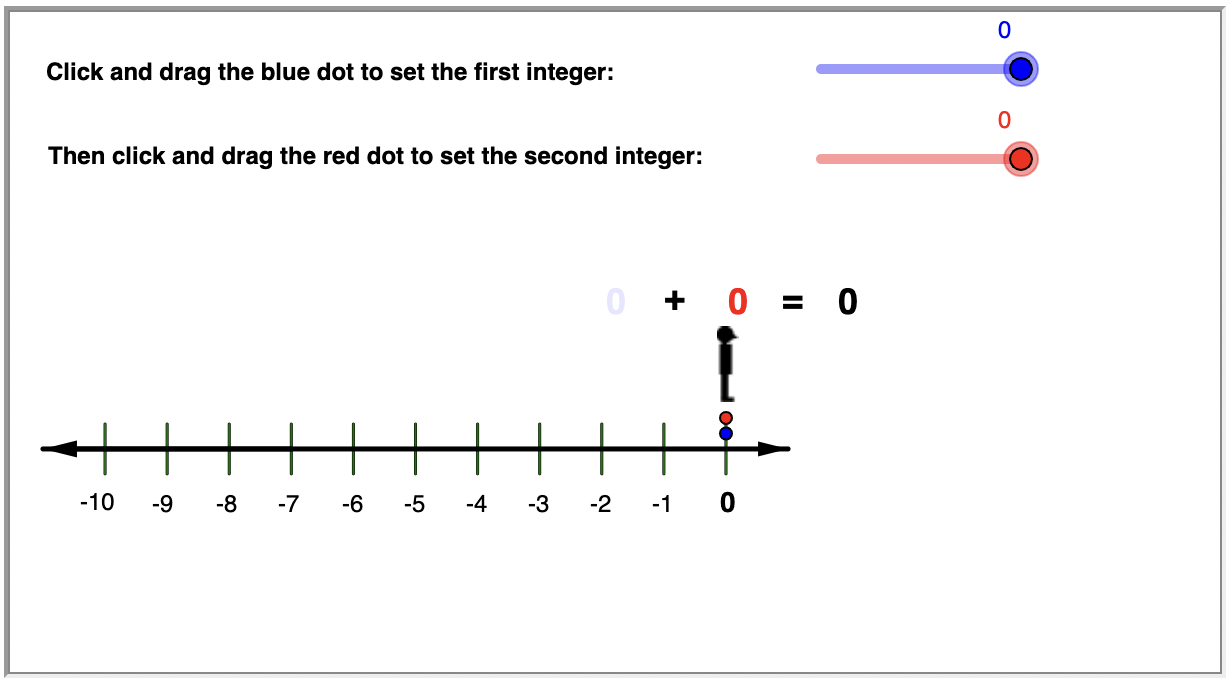
$Screen Shot 2021-05-20 a las 8.32.46 PM.png$

En ambos casos, el número total de unidades movidas es la distancia total desplazada. Dado que la distancia de un número a partir de 0 es el valor absoluto de ese número, entonces el valor absoluto de la suma de los enteros es la suma de los valores absolutos de los agregados.

Cuando ambos números son negativos, te mueves hacia la izquierda en una dirección negativa, y la suma es negativa. Cuando ambos números son positivos, te mueves hacia la derecha en una dirección positiva, y la suma es positiva.

Para sumar dos números con el mismo signo (ambos positivos o ambos negativos):

Sumar sus valores absolutos y dar a la suma el mismo signo.

Ejemplo

Encuentra -23+ (-16).

Solución

Ambas adiciones tienen el mismo signo (negativo).

Entonces, sumar sus valores absolutos:

|-23|=23 y |-16|=16

La suma de esos números es 23+16=39.

Dado que ambas adiciones son negativas, la suma es negativa.

-23+ (-16) =-39

Con más de dos adiciones que tengan el mismo signo, utilice el mismo proceso con todas las adiciones.

Ejemplo

Encuentra -27+ (-138) + (-55).

Solución

Todas las adiciones tienen el mismo signo (negativo).

Entonces, sumar sus valores absolutos:

|-27|=27, |-138|=138 y |-55|=55

La suma de esos números es 27+138+55=220.

Dado que todas las adiciones son negativas, la suma es negativa.

-27+ (-138) + (-55) =-220

Ejercicio

Encuentra -32+ (-14).

Contestar

Incorrecto. Encontraste la suma de los valores absolutos, pero la suma debe ser negativa, ya que estás sumando dos números negativos. La respuesta correcta -46
Incorrecto. Le restaste 14 de 32. La suma se encuentra sumando primero los valores absolutos de las adiciones: |-32|+|-14|=32+14=46. Entonces debes darle a la suma la misma señal que las dos adiciones. La respuesta correcta es -46.
Incorrecto. La suma se encuentra sumando primero los valores absolutos de las adiciones: |-32|+|-14|=32+14=46. Entonces debes darle a la suma la misma señal que las dos adiciones. La respuesta correcta es -46.
Correcto. La suma se encuentra sumando primero los valores absolutos de las adiciones: |-32|+|-14|=32+14=46. Entonces debes darle a la suma la misma señal que las dos adiciones, por lo que la respuesta es -46.

Adición de números enteros con signos diferentes

¿Qué sucede cuando los agregados tienen diferentes signos, como en el problema de temperatura en la introducción? Si es -10 grados, y luego la temperatura sube 8 grados, la nueva temperatura es -10+8. ¿Cómo se puede calcular la nueva temperatura?

Cuando agrega un entero positivo y un entero negativo, se mueve en la dirección positiva (derecha) al primer número, y luego se mueve en la dirección negativa (izquierda) para agregar el entero negativo.

Dado que las distancias se superponen, el valor absoluto de la suma es la diferencia de sus distancias. Entonces, para sumar un número positivo y un número negativo, restas sus valores absolutos (sus distancias de 0).

Actividad interactiva suplementaria

Intenta sumar números enteros con diferentes signos con esta línea numérica interactiva. Muévase en una dirección positiva (derecha) para agregar un número positivo, y muévase en una dirección negativa (izquierda) para agregar un número negativo. Consulta si puedes encontrar una regla para sumar números sin usar la línea numérica.

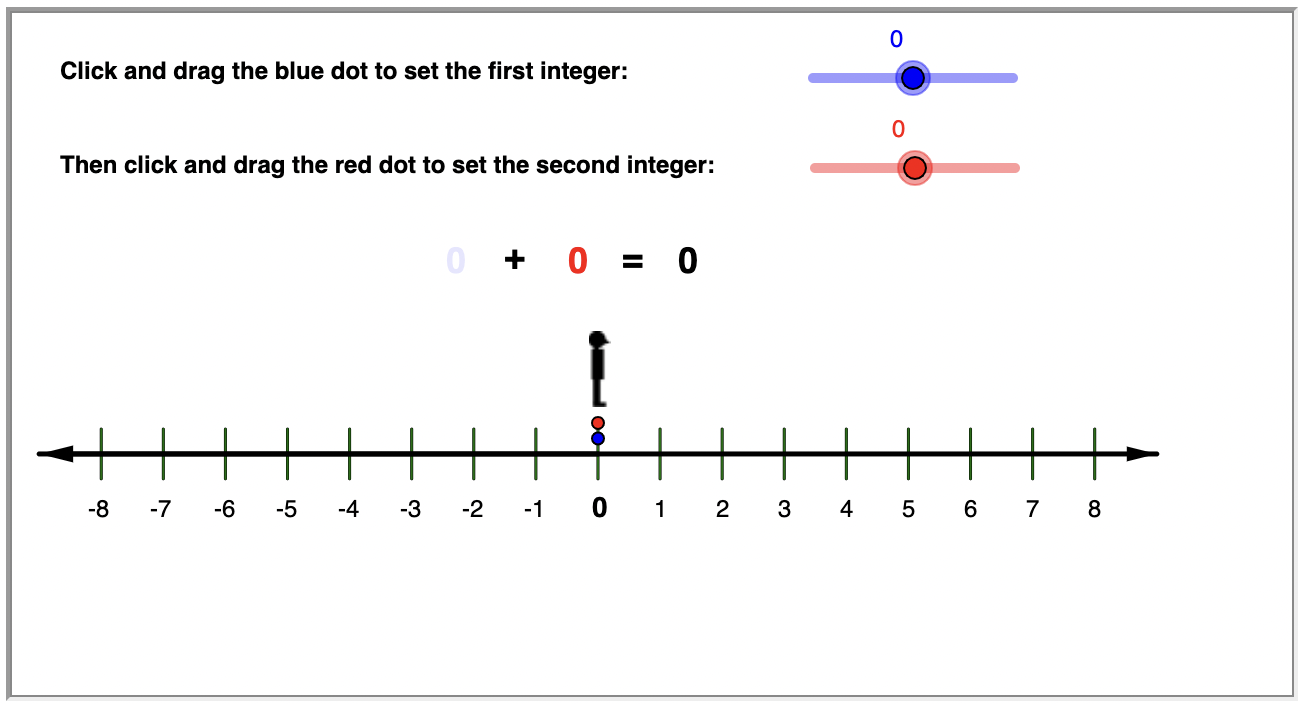
$Screen Shot 2021-05-21 a las 12.48.24 PM.png$

¿Cuál es el signo de la suma de un entero positivo y uno negativo? Es bastante fácil de entender. Si te moviste más a la derecha que a la izquierda, terminaste a la derecha de 0, y la respuesta es positiva; y si te mueves más hacia la izquierda, la respuesta es negativa.

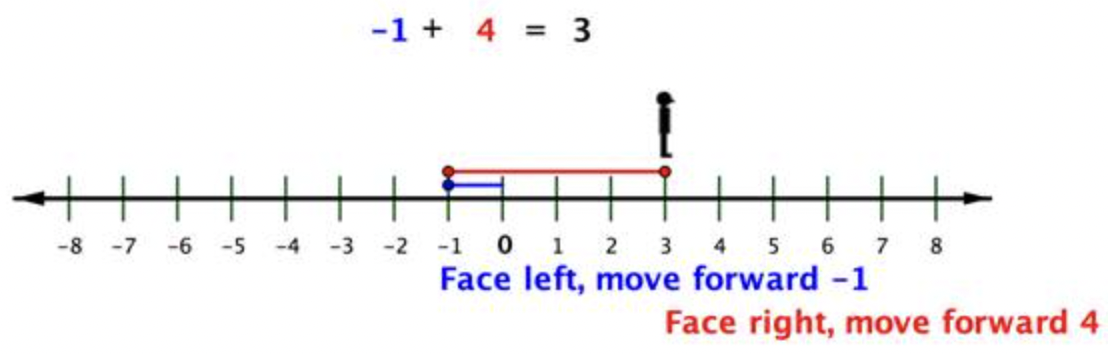
$Screen Shot 2021-05-21 a las 12.49.31 PM.png$

Si no tenías la línea numérica a la que hacer referencia, podrías encontrar la suma de -1+4 por

restando las distancias de cero (los valores absolutos) 4-1=3 y luego
aplicando el signo del más alejado de cero (el mayor valor absoluto). En este caso, 4 está más lejos de 0 que -1, por lo que la respuesta es positiva: -1+4=3

Mira la ilustración a continuación.

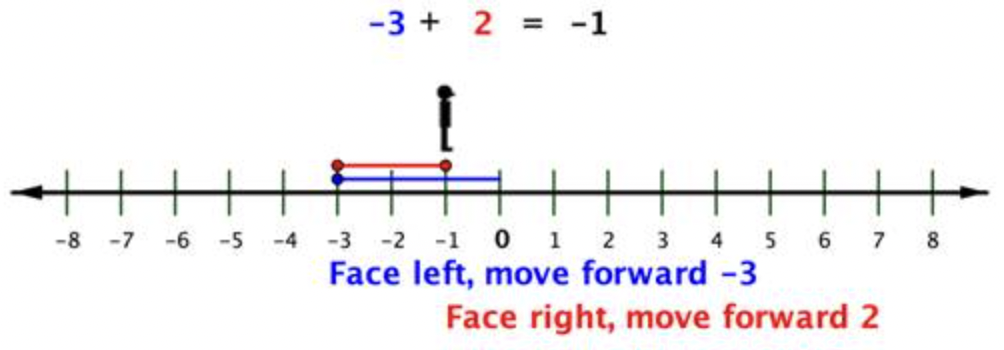
$Screen Shot 2021-05-21 a las 12.53.40 PM.png$

Si no tenías la línea numérica a la que hacer referencia, puedes encontrar la suma de -3+2 por

restando las distancias de cero (los valores absolutos) 3-2=1 y luego
aplicando el signo del más alejado de cero (el mayor valor absoluto). En este caso, |-3|>|2|, por lo que la respuesta es negativa: -3+2=-1

Para sumar dos números con signos diferentes (uno positivo y otro negativo):

Encuentra la diferencia de sus valores absolutos.
Dar a la suma el mismo signo que el número con el mayor valor absoluto.

Tenga en cuenta que cuando encuentre la diferencia de los valores absolutos, siempre resta el valor absoluto menor del mayor. El siguiente ejemplo te muestra cómo resolver la cuestión de temperatura que consideraste antes.

Ejemplo

Encuentra 8+ (-10).

Solución

Los apéndigos tienen diferentes signos.

Así que encuentra la diferencia de sus valores absolutos.

|-10|=10 y |8|=8

La diferencia de los valores absolutos es 10-8=2.

Desde 10>8, la suma tiene el mismo signo que -10.

8+ (-10) =-2

Ejemplo

Evaluar$\ x+37$ cuándo$\ x=-22$.

Solución

$\ x+37$

$\ -22+37$

Sustituto$\ -22$$\ x$ en la expresión.

$\ |-22|=22 \text { and }|37|=37$

$\ 37-22=15$

Los apéndigos tienen diferentes signos. Así que encuentra la diferencia de sus valores absolutos.

Desde |37|>|-22|, la suma tiene el mismo signo que 37.

-22+37=15

Con más de dos adiciones, se pueden agregar los dos primeros, luego el siguiente, y así sucesivamente.

Ejemplo

Encuentra -27+ (-138) +55.

Solución

	Agrega dos a la vez, empezando por -27+ (-138).
\ (\\ begin {array} {c} \|-27\|=27\ text {y} \|-138\|=138\\ 27+138=165\\ -27+-138=-138=-165 \ end {array}\)	Ya que tienen los mismos signos, se agregan sus valores absolutos y se usa el mismo signo para obtener -165.
\ (\\ begin {array} {c} -165+55\\ \|-165\|=165\ text {y} \|55\|=55\\ 165-55=110 \ end {array}\)	Ahora agrega -165+55. Dado que -165 y 55 tienen signos diferentes, los sumas restando sus valores absolutos.
$\ -165+55=-110$	Desde 165>55, el signo de la suma final es el mismo que el signo de -165.

$\ -27+(-138)+55=-110$

Ejercicio

Encuentra 32+ (-14).

Contestar

Incorrecto. Encontraste la suma de los valores absolutos. Dado que las adiciones tienen signos diferentes, se debe encontrar la diferencia de los valores absolutos. |32|=32 y |-14|=14. La diferencia es 32-14=18. El signo de la suma es el mismo que el adenda con el mayor valor absoluto. Desde |32|>|-14|, la suma es positiva, el mismo signo que 32. La respuesta correcta es 18.
Correcto. Dado que las adiciones tienen signos diferentes, se debe encontrar la diferencia de los valores absolutos. |32|=32 y |-14|=14. La diferencia es 32-14=18. El signo de la suma es el mismo que el adenda con el mayor valor absoluto. Desde |32|>|-14|, la suma es positiva.
Incorrecto. Encontró la diferencia de los valores absolutos de las adiciones. Sin embargo, debido a que |32|>|-14|, el signo de la suma debe ser el mismo signo que 32. La respuesta correcta es 18.
Incorrecto. Añadió los valores absolutos de las adiciones, y le dio a la suma la señal equivocada. Dado que las adiciones tienen signos diferentes, se debe encontrar la diferencia de los valores absolutos. |32|=32 y |-14|=14. La diferencia es 32-14=18. El signo de la suma es el mismo que el adenda con el mayor valor absoluto. Desde |32|>|-14|, la suma es positiva, el mismo signo que 32. La respuesta correcta es 18.

Resumen

Hay dos casos a considerar a la hora de sumar enteros. Cuando los signos son los mismos, se agregan los valores absolutos de los agregados y se usa el mismo signo. Cuando los signos son diferentes, encuentras la diferencia de los valores absolutos y usas el mismo signo que el adenda con el mayor valor absoluto.