10.2.1: Resolver desigualdades de un solo paso
- Page ID
- 111423
- Representar desigualdades en una recta numérica.
- Utilizar la propiedad de adición de la desigualdad para aislar variables y resolver desigualdades algebraicas, y expresar sus soluciones gráficamente.
- Utilizar la propiedad multiplicadora de la desigualdad para aislar variables y resolver desigualdades algebraicas, y expresar sus soluciones gráficamente.
Introducción
A veces hay un rango de valores posibles para describir una situación. Cuando ves una señal que dice “Límite de velocidad 25”, sabes que eso no significa que tengas que conducir exactamente a una velocidad de 25 millas por hora (mph). Esta señal significa que no se supone que vayas a más de 25 mph, pero hay muchas velocidades legales que podrías conducir, como 22 mph, 24.5 mph o 19 mph. En una situación como esta, que tiene más de un valor aceptable, las desigualdades se utilizan para representar la situación en lugar de ecuaciones.
¿Qué es una Desigualdad?
Una desigualdad es una afirmación matemática que compara dos expresiones usando un signo de desigualdad. En una desigualdad, una expresión de la desigualdad puede ser mayor o menor que la otra expresión. En estas declaraciones se utilizan símbolos especiales. El cuadro de abajo muestra el símbolo, el significado y un ejemplo para cada signo de desigualdad.
\(\ x \neq y \quad x \text{ is} {\bf\text { not equal }}\text{to } y\).
Ejemplo: El número de días en una semana no es igual a 9.
\(\ x>y \quad x {\bf\text { is greater than }} y . \text { Example: } 6>3\)
Ejemplo: El número de días en un mes es mayor que el número de días en una semana.
\(\ x<y \quad x {\bf\text { is less than }} y\)
Ejemplo: El número de días en una semana es menor que el número de días en un año.
\(\ x \geq y \quad x {\bf\text { is greater than or equal to }} y\)
Ejemplo: 31 es mayor o igual al número de días en un mes.
\(\ x \leq y \quad x {\bf\text { is less than or equal to }} y\)
Ejemplo: La velocidad de un automóvil que conduce legalmente en una zona de 25 mph es menor o igual a 25 mph.
Lo importante de las desigualdades es que puede haber múltiples soluciones. Por ejemplo, la desigualdad “31 ≥ el número de días en un mes” es una verdadera declaración por cada mes del año, ningún mes tiene más de 31 días. Se mantiene cierto para enero, que tiene 31 días (\(\ 31 \geq 31\)); septiembre, que tiene 30 días (≥ 30); y febrero, que tiene ya sea 28 o 29 días dependiendo del año (\(\ 31 \geq 28 \text { and } 31 \geq 29\)).
La desigualdad también se\(\ x>y\) puede escribir como\(\ y<x\). Los lados de cualquier desigualdad pueden cambiarse siempre que el símbolo de desigualdad entre ellos también se invierta.
Representación de desigualdades en una recta numérica
Las desigualdades se pueden graficar en una recta numérica. A continuación se presentan tres ejemplos de desigualdades y sus gráficas.
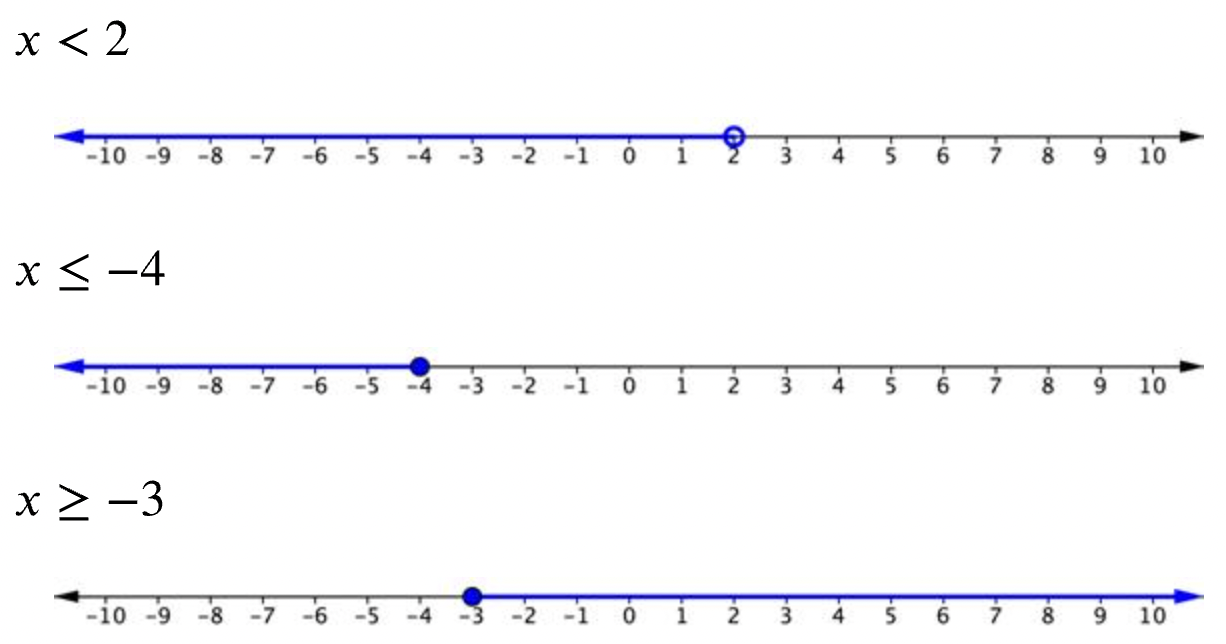
Cada una de estas gráficas comienza con un círculo, ya sea un círculo abierto o cerrado (sombreado). A este punto se le suele llamar el punto final de la solución. Un círculo cerrado, o sombreado, se utiliza para representar las desigualdades mayores o iguales a (≥) o menores o iguales a (≤). El punto es parte de la solución. Un círculo abierto se utiliza para mayor que (>) o menor que (<). El punto no forma parte de la solución.
La gráfica se extiende entonces sin cesar en una dirección. Esto se muestra mediante una línea con una flecha al final. Por ejemplo, observe que para la gráfica de arriba\(\ x \geq-3\) mostrada, el punto final es -3, representado con un círculo cerrado ya que la desigualdad es mayor o igual a -3. La línea azul se dibuja a la derecha en la recta numérica porque los valores en esta área son mayores que -3. La flecha al final indica que las soluciones continúan infinitamente.
Resolver desigualdades mediante propiedades de suma y resta
Se puede resolver la mayoría de las desigualdades utilizando los mismos métodos que los de resolución de ecuaciones. Las operaciones inversas se pueden utilizar para resolver desigualdades. Esto se debe a que cuando se suma o resta el mismo valor de ambos lados de una desigualdad, se ha mantenido la desigualdad. Estas propiedades se describen en el cuadro azul a continuación.
\(\ \text { If } a>b, \text { then } a+c>b+c\)
\(\ \text { If } a>b, \text { then } a-c>b-c\)
Debido a que las desigualdades tienen múltiples soluciones posibles, representar gráficamente las soluciones proporciona una visión útil de la situación. El siguiente ejemplo muestra los pasos para resolver y graficar una desigualdad.
Resolver para\(\ x\).
\(\ x+3<5\)
Solución
| \ (\\ begin {array} {r} x+3<&5\\ \ -3\\\\ &\ -3\ \ hline x\\\\\\\\ <&2 \ end {array}\\) |
Aislar la variable restando 3 de ambos lados de la desigualdad. |
\(\ x<2\)
A continuación\(\ x<2\) se muestra la gráfica de la desigualdad.

Así como puedes verificar la solución a una ecuación, puedes verificar una solución a una desigualdad. Primero, se comprueba el punto final sustituyéndolo en la ecuación relacionada. Entonces se comprueba para ver si la desigualdad es correcta sustituyendo cualquier otra solución para ver si es una de las soluciones. Debido a que existen múltiples soluciones, es una buena práctica verificar más de una de las posibles soluciones. Esto también puede ayudarte a verificar que tu gráfica sea correcta.
El siguiente ejemplo muestra cómo se podría comprobar que\(\ x<2\) es la solución a\(\ x+3<5\).
Comprobar que\(\ x<2\) es la solución para\(\ x+3<5\).
Solución
| \ (\\ begin {alineado} x+3 &=5\\ \ text {Hace} 2+3 &=5? \\ 5 &=5 \ final {alineado}\) |
Sustituir el punto final 2 en la ecuación relacionada,\(\ x+3=5\). |
|
\ (\\ begin {alineado} ¡Comproba! |
Elija un valor menor que 2, como 0, para verificar la desigualdad. (Este valor estará en la parte sombreada de la gráfica.) |
\(\ x<2\)es la solución para\(\ x+3<5\)
Los siguientes ejemplos muestran problemas adicionales de desigualdad. También se muestra la gráfica de la solución a la desigualdad. Acuérdate de revisar la solución. ¡Este es un buen hábito para construir!
Resolver para\(\ x\).
\(\ \frac{15}{2}+x>-\frac{37}{4}\)
Solución
| \ (\\ begin {array} {r} \ frac {15} {2} -\ frac {15} {2} +x-\ frac {37} {4} -\ frac {15} {2}\\ x>-\ frac {37} {4} -\ frac {15} {2}\ x>-\ frac {37} {4} -\ frac {30} {4}\\ x>-\ frac {67} {4} \ end {array}\) |
Restar\(\ \frac{15}{2}\) de ambos lados para aislar la variable. |
\(\ x>-\frac{67}{4}\)
Resolver para\(\ x\).
\(\ x-10 \leq-12\)
Solución
| \ (\\ begin {array} {r} x-10\ leq&\ -12\\\ +10 \\\\ &\ +10\\\ hline x \\\\\ hline x\\\\\\\\\ leq&\ -2 \ end {array}\) |
Aísle la variable sumando 10 a ambos lados de la desigualdad. |
\(\ x \leq-2\)
La gráfica de esta solución se muestra a continuación. Observe que se usa un círculo cerrado porque la desigualdad es “menor o igual a” (≤). La flecha azul se dibuja a la izquierda del punto -2 porque estos son los valores que son menores que -2.
Comprobar que \(\ x \leq-2\)es la solución para\(\ x-10 \leq-12\).
Solución
| \ (\\ begin {alineado} x-10 &=-12\ \ text {Hace} -2-10 &=-12? \\ -12 &=-12 \ final {alineado}\) |
Sustituya el punto final -2 en la ecuación relacionada\(\ x-10=-12\). |
|
\ (\\ text {Es}\ begin {alineado} ¡Comproba! |
Elija un valor menor que -2, como -5, para verificar la desigualdad. (Este valor estará en la parte sombreada de la gráfica.) |
\(\ x \leq-2\)es la solución a\(\ x-10 \leq 12\).
Resolver para\(\ a\).
\(\ a-17>-17\)
Solución
| \ (\\ begin {array} {r} a-17>&\ -17\\ \ +17\\\\\ &\ +17\\ \ hline a\\\\\\\\\\ >&0 \ end {array}\) |
Aísle la variable sumando 17 a ambos lados de la desigualdad. |
\(\ a>0\)
La gráfica de esta solución se muestra a continuación. Observe que se usa un círculo abierto porque la desigualdad es “mayor que” (>). La flecha se dibuja a la derecha de 0 porque estos son los valores que son mayores que 0.

Comprobar que\(\ a>0\) es la solución para
\(\ a-17>-17\).
Solución
| \ (\\ begin {alineado} a-17 &=-17\\ \ text {Hace} 0-17 &=-17? \\ -17&=-17 \ final {alineado}\) |
Sustituya el punto final, 0, en la ecuación relacionada. |
|
\ (\\ begin {alineado} ¡Comproba! |
Elija un valor mayor que 0, como 20, para verificar la desigualdad. (Este valor estará en la parte sombreada de la gráfica.) |
\(\ a>0\)es la solución a\(\ a-17>-17\).
Resolver para\(\ x\):\(\ 0.5 x \leq 7-0.5 x\).
- \(\ x \leq 0\)
- \(\ x>35\)
- \(\ x \leq 7\)
- \(\ x \geq 5\)
- Contestar
-
- Incorrecto. Para encontrar el valor de\(\ x\), intente agregar\(\ 0.5 x\) a ambos lados. La respuesta correcta es\(\ x \leq 7\).
- Incorrecto. Para encontrar el valor de\(\ x\), intente agregar\(\ 0.5 x\) a ambos lados. La respuesta correcta es\(\ x \leq 7\).
- Correcto. Cuando se agrega\(\ 0.5 x\) a ambos lados se crea\(\ 1 x\), entonces\(\ x \leq 7\).
- Incorrecto. Para encontrar el valor de\(\ x\), intente agregar\(\ 0.5 x\) a ambos lados. La respuesta correcta es\(\ x \leq 7\).
Resolver desigualdades que implican multiplicación
Resolver una desigualdad con una variable que tenga un coeficiente distinto a 1 generalmente implica multiplicación o división. Los pasos son como resolver ecuaciones de un solo paso que implican multiplicación o división EXCEPTO por el signo de desigualdad. Veamos qué pasa con la desigualdad cuando multiplicas o divides cada lado por el mismo número.
| Empecemos con la verdadera afirmación: | \(\ 10>5\) | Intentemos de nuevo comenzando con la misma afirmación verdadera: | \(\ 10>5\) |
| A continuación, multiplica ambos lados por el mismo número positivo: | \(\ 10 \cdot 2>5 \cdot 2\) | Esta vez, multiplique ambos lados por el mismo número negativo: | \(\ 10 \cdot-2>5 \cdot-2\) |
| 20 es mayor que 10, así que todavía tienes una verdadera desigualdad: | \(\ 20>10\) | ¡Espera un minuto! -20 no es mayor que -10, por lo que tiene una declaración falsedad. | \(\ -20>-10\) |
| Cuando multiplicas por un número positivo, ¡deja el signo de desigualdad tal como está! | Se debe “revertir” el signo de desigualdad para que la afirmación sea cierta: | \(\ -20<-10\) |
Cuando multiplicas por un número negativo, “invierte” el signo de desigualdad.
Siempre que multipliques o dividas ambos lados de una desigualdad por un número negativo, el signo de desigualdad debe revertirse para mantener una declaración verdadera.
Estas reglas se resumen en el recuadro que aparece a continuación.
\ (\\ comenzar {alineado}
\ texto {Si} a>b\ texto {, entonces} a c>b c\ texto {, si} c>0\\
\ texto {Si} a>b\ texto {, entonces} a c<b c\ texto {, if} c<0\\\
\ texto {Si} a>b\ texto {, entonces}\ frac {a} {c} >\ frac {b} {c}\ texto {, si} c>0\\
\ texto {Si} a>b\ texto {, entonces}\ frac {a} {c} <\ frac {b} {c}\ texto {, si} c<0
\ end {alineado}\)
Ten en cuenta que solo cambias el signo cuando estás multiplicando y dividiendo por un número negativo. Si suma o resta un número negativo, la desigualdad permanece igual.
Resolver para\(\ x\).
\(\ -\frac{1}{3}>-12 x\)
Solución
| \ (\\ comenzar {alineado} -\ frac {1} {3}\ div-12&<-12 x\ div-12\ -\ frac {1} {3}\ cdot-\ frac {1} {12} &<\ frac {-12 x} {-12}\ \ frac {1} {36} &<x \ end {alineado}\) |
Divide ambos lados por -12 para aislar la variable. Como estás dividiendo por un número negativo, necesitas cambiar la dirección del signo de desigualdad. |
|
Comprobar \ (\\ begin {aligned}\ text {Does} |
Verifique su solución comprobando primero el punto final,\(\ \frac{1}{36}\), en la ecuación relacionada. |
|
\ (\\ begin {alineado} ¡Comproba! |
Elija un valor mayor que\(\ \frac{1}{36}\), como 2, para verificar la desigualdad. |
\(\ x>\frac{1}{36}\)
Resolver para\(\ x\).
\(\ 3 x>12\)
Solución
| \ (\\ comenzar {alineado} \ frac {3 x} {3} &>\ frac {12} {3}\\ & x>4 \ final {alineado}\) |
Divide ambos lados por 3 para aislar la variable. |
|
Comprobar \ (\\ begin {alineado} \ (\\ begin {alineado} |
Verifique su solución primero verificando el punto final, 4, y luego verificando otra solución para detectar la desigualdad. |
\(\ x>4\)
A continuación se muestra la gráfica de esta solución.

No hubo necesidad de hacer ningún cambio en el signo de desigualdad porque ambos lados de la desigualdad se dividieron por positivos 3. En el siguiente ejemplo, hay división por un número negativo, ¡así que hay un paso adicional en la solución!
Resolver para\(\ x\).
\(\ -2 x>6\)
Solución
|
\(\ \frac{-2 x}{-2}<\frac{6}{-2}\) \(\ x<-3\) |
Dividir cada lado de la desigualdad entre -2 para aislar la variable, y cambiar la dirección del signo de desigualdad debido a la división por un número negativo. |
|
Comprobar: \ (\\ begin {alineado}\ text {Hace} ¡Comproba! |
Verifique su solución primero verificando el punto final, -3, y luego verificando otra solución para detectar la desigualdad. |
\(\ x<-3\)
Debido a que ambos lados de la desigualdad se dividieron por un número negativo, -2, el símbolo de desigualdad se cambió de > a <. A continuación se muestra la gráfica de esta solución.

Resolver para\(\ y\):\(\ -10 y \geq 150\)
- \(\ y=-15\)
- \(\ y \geq-15\)
- \(\ y \leq-15\)
- \(\ y \geq 15\)
- Contestar
-
- Incorrecto. Si bien -15 es una solución a la desigualdad, no es la única solución. La solución debe incluir un signo de desigualdad. La respuesta correcta es\(\ y \leq-15\).
- Incorrecto. Esta solución no satisface la desigualdad. Por ejemplo\(\ y=0\), que es un valor mayor que -15, da como resultado una declaración falsedad. 0 no es mayor que Al dividir por un número negativo, debe cambiar el símbolo de desigualdad. La respuesta correcta es\(\ y \leq-15\).
- Correcto. Dividiendo ambos lados por -10 hojas\(\ y\) aisladas en el lado izquierdo de la desigualdad y -15 en el derecho. Ya que dividiste por un número negativo, el ≥ debe cambiarse a ≤.
- Incorrecto. Dividir por -10, no 10, para aislar la variable. La respuesta correcta es\(\ y \leq-15\).
Resolver para\(\ a\):\(\ -\frac{a}{5}<\frac{35}{8}\)
- \(\ a>-\frac{175}{8}\)
- \(\ a<-\frac{175}{8}\)
- \(\ a>-\frac{7}{8}\)
- \(\ a<-\frac{7}{8}\)
- Contestar
-
- Correcto. Al multiplicar ambos lados por -5 y voltear el signo de desigualdad < to >, lo encontraste\(\ a>-\frac{175}{8}\).
- Incorrecto. Se multiplicó correctamente por -5, pero recuerde que el signo de desigualdad se voltea cuando se multiplica por un número negativo. La respuesta correcta es:\(\ a>-\frac{175}{8}\).
- Incorrecto. Parece que dividiste ambos lados por -5. Si bien recordaste voltear correctamente el signo de desigualdad, la división no es la operación correcta aquí. La respuesta correcta es:\(\ a>-\frac{175}{8}\).
- Incorrecto. Parece que dividiste ambos lados por -5. La división no es la operación correcta aquí, y recuerda voltear el signo de desigualdad cuando multipliques o divides por un número negativo. La respuesta correcta es:\(\ a>-\frac{175}{8}\).
Resumen
Resolver desigualdades es muy similar a resolver ecuaciones, excepto que hay que revertir los símbolos de desigualdad cuando multiplicas o divides ambos lados de una desigualdad por un número negativo. Dado que las desigualdades pueden tener múltiples soluciones, es costumbre representar la solución a una desigualdad tanto gráfica como algebraicamente. Debido a que suele haber más de una solución a una desigualdad, cuando revisas tu respuesta debes verificar el punto final y otro valor para verificar la dirección de la desigualdad.


